桩土土拱结构有限元分析

（福建水利电力职业技术学院，福建 永安 366000）

1 研究背景

目前我国已建成各类水库9万多座，由于大部分兴建于建国初期，受当时施工条件和施工技术的限制，许多成为病险或为病险隐患水库。滑坡作为一种地质灾害广泛存在于世界各国各地区，是水库病险隐患重要原因之一。处理措施中，抗滑桩相比于其它工程措施，例如抗滑挡墙、排水、消方减载、预应力锚杆等，是一种被实践证明效果较佳的滑坡处理方法，经常被用于水库库区岸坡稳定和滑坡防治之中，特别是深层的滑坡。抗滑桩设于滑坡的适当部位，一般完全埋置在地面下，有时也可露出地面，但桩的末段必须埋置于滑动面以下稳固地层一定深度。抗滑桩是利用桩与周围岩、土体的共同作用，把部分滑坡推力传到稳定地层，即利用稳定地层的锚固作用和被动抗力，来抗衡滑坡体的下滑推力。

抗滑桩与周围土体形成的土拱与普通拱结构不同。普通拱结构是把材料制成拱形状，充分发挥材料抗压能力大的特点来承受，而抗滑桩与土体形成的土拱有其自身独特的形成过程：在荷载或自重的作用下，土体发生压缩和变形，从而产生不均匀沉降，致使土颗粒间产生互相楔紧的作用，于是在一定范围土层中产生“拱效应”，土粒间的黏聚力和摩擦力是形成土拱的先决条件。如图示1所示。

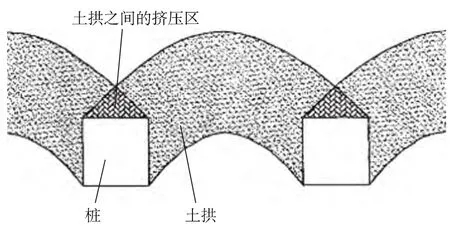
图1 土拱效应示意图

研究表明，抗滑桩的合理布置间距对土拱的形成和土拱效应的发挥是一个重要的影响因素。合理的间距可以通过土力学的相关知识和假定推导出合理的桩距计算公式。随着计算机水平的发展和数值模拟软件的进步，可以通过数值模拟软件来模拟导出合理桩距。

2 土拱效应的有限元模型

桩-土相互作用实际上是三维空间问题，但如果只考虑桩土间的土拱效应及其形成机理，可以把此问题简化成二维的平面问题来考虑，假定桩变位为零，桩周土体间变形协调，如图2所示。

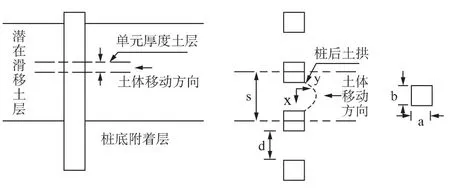
图2 桩土作用示意图

针对土拱效应问题，一般有有限差分法和有限元[9]来解决，本文用有限元法来模拟计算分析，模型如图3所示。

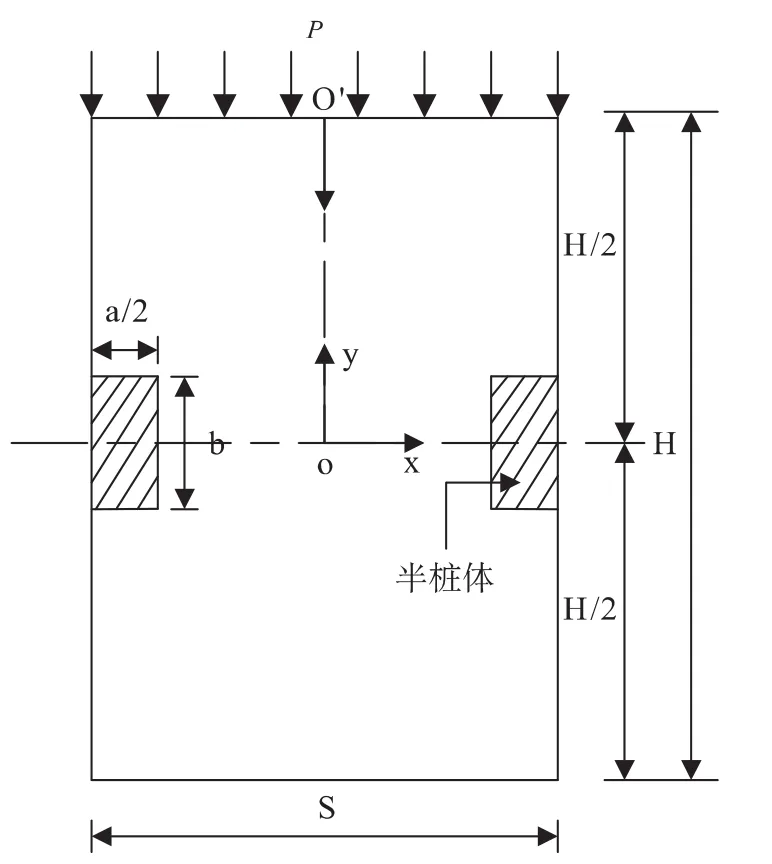
图3 有限单元法模型

桩周土体采用弹塑性模型，符合Mohr-Coulomb屈服准则，其表达式为：σ1-σ3／2=（σ1+σ3）sinφ／2+c·cosφ；抗滑桩采用线弹性模型。由于滑坡推力P是不均匀的体力，在有限元力加载时可通过等重力转化为均匀的体力。下面以一算例运用有限元方法来分析桩土间土体形成土拱效应状态，桩间距与桩宽必须满足的关系。

3 算例分析

某抗滑桩工程，S=5m，H=20m，a=2m，b=2m，l=10m，P=265t／m。计算所采用的物理力学参数见表1。

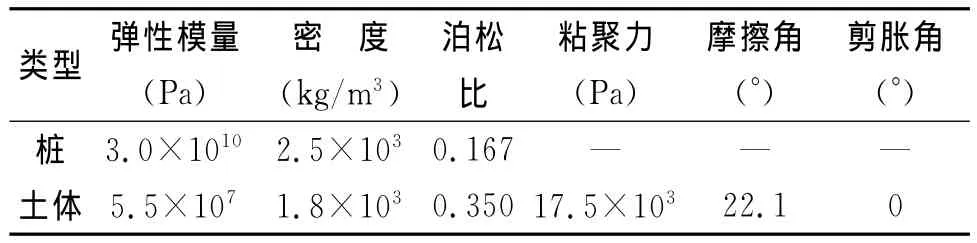
表1 计算参数

此有限元模型，桩和土体均采用平面4节点单元，桩土接触面采用接触单元，模型的网格划分如图4所示，共有1 222个节点，1 150个单元。模型底边施加X、Y两方向的位移约束，模型两边施加X方向的位移约束，抗滑桩各周边施加X、Y两方向的位移约束。

图4 有限元模型网格

桩后土体“土拱”效应可以通过中轴线OO′之Y方向的位移变化来反应。为了分析桩间距对“土拱”效应的影响，分别计算了S=4、5、6、7、8、9时，Y方向位移等值线图（图5～图10）。

以图6来说明土拱效应的形成。从图6中可以看出，桩周土体发生一定的位移后，模型整体处于稳定状态，亦说明了在桩距为5m时，抗滑桩起到了抗滑效果。桩后土体位移沿土体的滑动方向逐渐减小至零；桩间土体位移沿滑动方向先逐渐减小，至桩后约3m处位移达到最小值，后又沿滑动方向稍有增大。图6中表明有部分桩间土体处于两相等值E线之间，“土拱”亦在此间形成，对上部土体起到了支承作用，这主要是桩周土体间不等的位移变化引起的；靠近桩的等值E线延伸至桩间两侧，说明了桩内侧与土体间的摩擦对抗滑也起到了一定的作用。

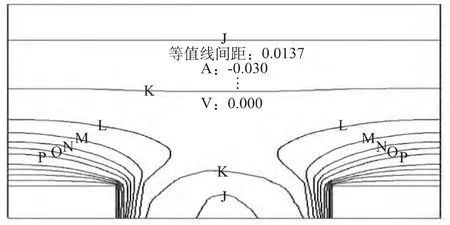
图5 桩后土体Y方向位移等值线图（桩距4m）

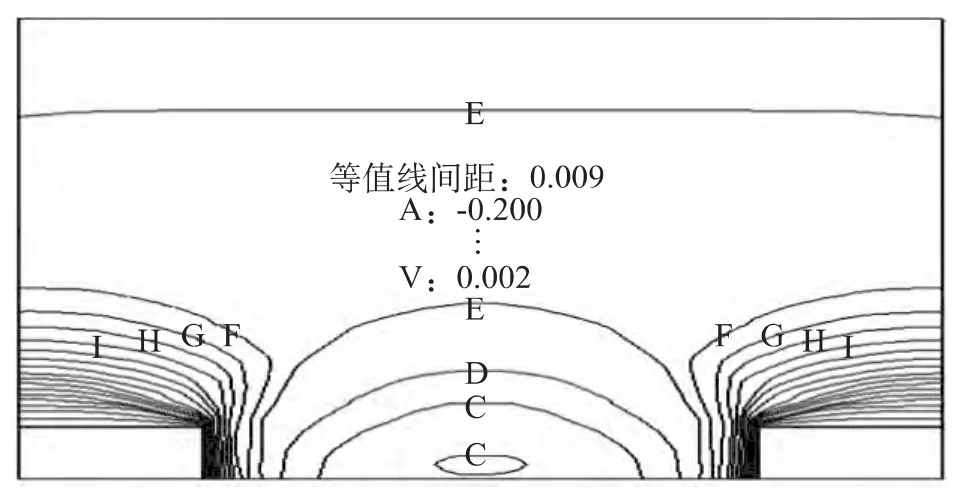
图6 桩后土体Y方向位移等值线图（桩距5m）

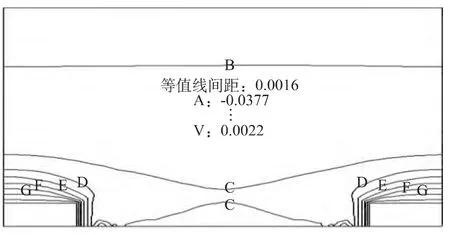
图7 桩后土体Y方向位移等值线图（桩距6m）

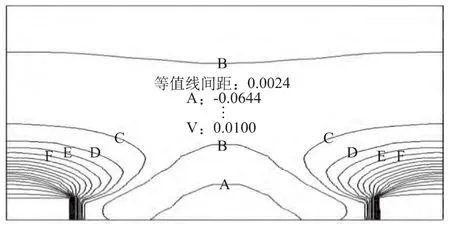
图8 桩后土体Y方向位移等值线图（桩距7m）

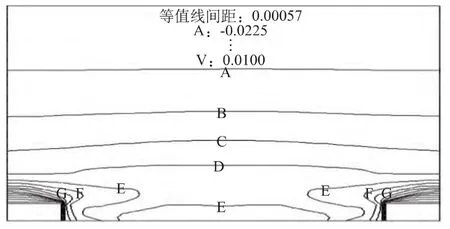
图9 桩后土体Y方向位移等值线图（桩距8m）

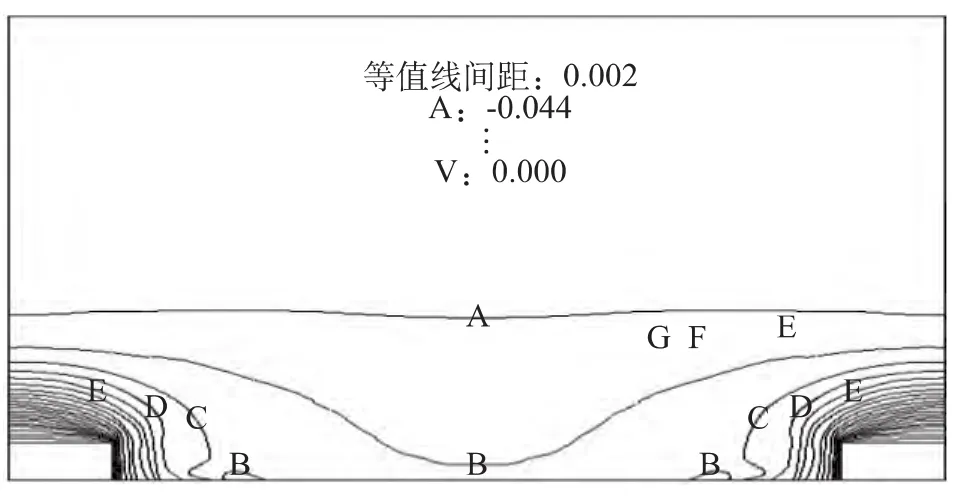
图10 桩后土体Y方向位移等值线图（桩距9m）

从以上各图可以看出在桩间距4m≤S≤7m时，桩后土体或大或小都形成一定的“土拱”，此间距称为“工程间距”；而在桩间距S≥8m时，桩后土体不再形成“土拱”。说明合理的桩间距是影响“土拱”形成的重要因素之一。比较图6～图9，可以看出在桩间距S=6m，即3倍桩宽时，“土拱”效果最好，亦称“结构间距”。当然这不是说桩间距不在工程间距或结构间距时，抗滑桩就不发挥抗滑作用。只要滑坡上作用有抗滑桩，都会对桩周附近产生一定的抗滑效果。

综上可知，在其他影响因素不变的情况下，欲在桩周土体形成“土拱”，桩间距一般取桩宽的2～3.5倍是比较适宜的。

根据各不等间距下的Y方向位移等值线图可以绘出模型中轴线OO′之Y方向位移的大致变化情况，即图11所示。

图11 模型中轴线OO′Y方向位移

从图11可以看出模型中轴线土体位移大致经历了y0→y3→y6→yn几个阶段，下面就各个阶段进行简要阐述：

y0→y3：土体大部分在两桩之间，由桩引起的“土拱”在此基本上不起作用，主要是两桩内侧与土体的摩擦起主要作用，离O点逆滑动方向，土体位移有稍微的增大。

→y3←：土体一般不再受桩内摩擦或作用极弱，且“土拱”作用效果极弱，土体位移达到相对最大值，约在桩上-0.3～0.8m处，即距O点约1.7～2.8m间。

y3→y6：土体受到“土拱”效应逐渐增强，此区土体沿随距O点逆滑动方向，土体位移在不断减小，即“土拱”作用在不断增大。

→y6←：土体受到的“土拱”作用最大，土体位移达到最小值，约在桩上2.0～3.0m处，即距O点约4.0～5.0m间。

y6→yn：土体受到的“土拱”效应在逐渐减弱，此区土体沿随距O点逆滑动方向，土体位移在不断增大，即“土拱”作用在不断减小。

→yn←：土体不再受“土拱”的作用，即土体位移主要受滑坡推力引起，土体位移在此达到一个稳定值，可能是最大值或相对最大值。

综上各区土体的分析，桩后“土拱”的作用范围在y3→y6→yn区间，即在此区范围内形成“土拱”效应。

4 结 论

滑坡或边坡设置抗滑桩后，桩周土体发生了不均匀位移和应力重分布，可充分发挥桩间、桩后土体的抗压与抗剪能力，形成土拱效应。合理的桩间距是土拱形成的前提，桩间距过大，不能形成土拱，反之过小，工程造价增加。从数值模拟结果可知，欲使抗滑桩在滑坡工程中出现土拱结构，必须使桩间距处于“工程间距”间，要取得最佳的效果，就必须使间距处于“结构间距”。本文通过对模拟结果的分析可知，桩间距一般取桩宽的2～3.5倍是比较合适的。如在没有计算参考或小工程施工时，为使工程既经济又满足工程需要，可以采用桩间距为桩宽的3倍。

[1]赵志峰，等.基于土拱效应围护桩间距的计算模型[J].南京林业大学学报自然科学版，2015，39（1）：130-134.

[2]王贤朋.被动桩土拱效应有限元差分模型研究[J].山西建筑，2015，（10）：58-60.

[3]铁道部第二勘测设计院.抗滑桩设计与计算[M].北京：中国铁道出版社，1983.

[4]吴子树.土拱形成机理及存在条件的探讨[J].成都科技大学学报，1995，（2）：15-19.

[5]贾海莉，等.关于土拱效应的几个问题[J].西南交通大学学报，2003，8（4）：398-402.

[6]王成华，等.抗滑桩间土拱力学特性与最大桩间距分析[J].山地学报，2001，19（6）：556-559.