基于CCS-MUSIC的宽带无模糊测频方法研究

常 虹

（西安邮电大学 通信与信息工程学院，陕西 西安710121）

0 引 言

频率估计是电子侦察中信号参数估计的基本问题，其中经典算法有离散傅立叶变换（Discrete Fourier Transform，DFT）算法和特征子空间算法等.DFT运算简单，但易受到瑞利限影响，导致测频精度不高［1］.典型的特征子空间算法如多信号子空间分类MUSIC算法、旋转不变子空间ESPRIT（Estimation of Signal Parameters via Rotational Invariance Techniques，ESPRIT）算法［2-3］，其频率估计性能优于DFT，可用于中等信噪比条件下信号的频率估计.基于当前的技术状况和硬件水平，对宽频段信号进行高速采样后的实时处理是很难的，存在AD和DSP速度不匹配的问题，欠采样可有效降低数据率，但引起的信号频谱混叠需要辅助解频率模糊算法解决.基于延时相位差的无模糊频率估计方法具有计算简单、方便的特点［4-5］，但相位误差引起的测频误差常常在MHz量级以上，无法满足现代电子战环境下接收机对测频精度的要求；文献［6］的前后向稀疏线性预测方法和文献［7］的MUSIC方法均基于多个延时通路实现无模糊频率估计，以增加硬件为代价，且延时精度无法保证，后者还需要预先知道信号个数，存在较大搜索步长时性能下降较多的问题；文献［8］对输入信号采用多路不同速率的AD进行采样，联合多路采样值并利用多维整数搜索解频率模糊，运算量较大，要求采样频率满足参差关系.

为了提高宽频带接收时信号频率的估计精度，同时保持较低的运算量，本文采用两个速率不同的AD对输入信号进行欠采样，计算CCS，只要识别出正确的谱峰位置就可获得信号的频率.但在同时多信号情况下，互相关频谱分布中，部分谱峰即“真峰”对应信号频率，部分谱峰即“伪峰”对应交调信号频率，本文提出在CCS峰附近设置搜索区间，并运用MUSIC算法在该区间上分别对由两个欠采样序列各自构造的特征子空间在该区间进行搜索的快速识别“伪峰”的方法，该方法可有效解决宽带侦收时同时多信号的无模糊频率估计的问题.

1 算法原理

假设同时输入频率分别为｛F1，F2，…，FI｝的I个复指数信号，对该混合信号分别以采样速率Fs1和Fs2进行欠采样，即max｛Fs1，Fs2｝＜2max｛F1，F2，…，FI｝.采样序列分别表示为

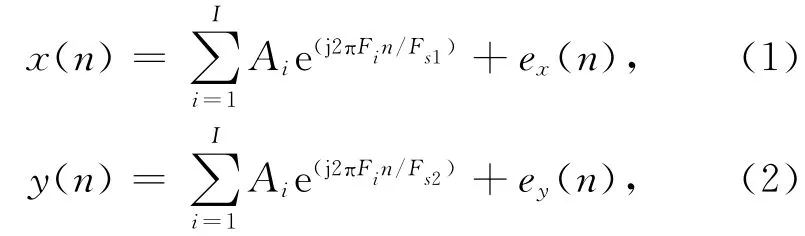
式中：Ai表示第i个信号的幅值.定义两个序列的互相关运算为

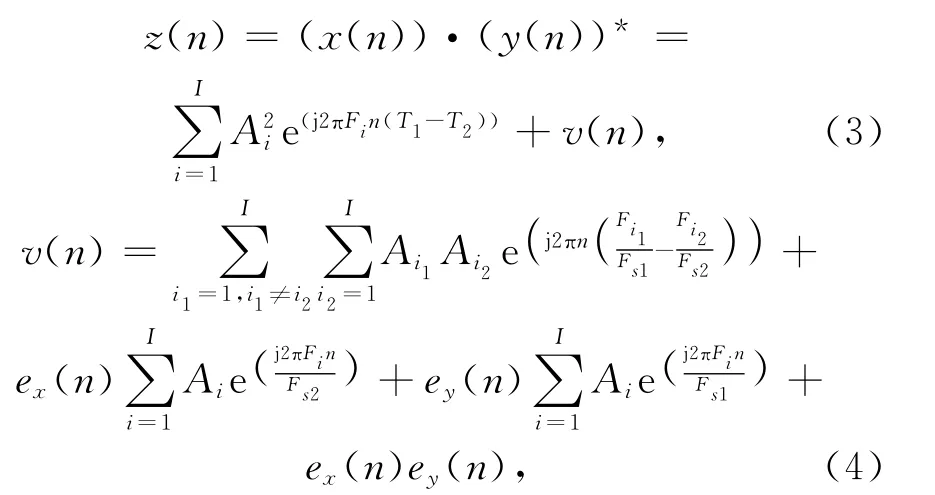
式中：T1=1／Fs1；T2=1／Fs2；v（n）为交调信号、信号与噪声乘积、噪声与噪声乘积之和.当|Fi（T1-T2）|＜1成立时，对z（n）作频域变换得到CCS分布，其中部分谱峰对应信号频率，部分谱峰对应交调信号频率.

接下来介绍如何用MUSIC搜索法识别“真峰”.根据CCS的分布，在每个CCS峰附近选定频率搜索区间，运用MUSIC算法在该区间上分别对由两个欠采样序列各自构造的特征子空间进行搜索，若CCS峰对应信号频率，两路MUSIC谱在该频率搜索区间会同时出现最大值，即判断该CCS峰为“真峰”，否则为“伪峰”.由特征子空间的最大特征值数量确定信号个数I后，对各相关谱峰处的联合MUSIC谱值由大到小排序，前I个值对应的频率搜索区间就是I个信号频率所在区间，位于这I个区间的CCS峰即对应信号频率.

分别以采样速率Fs1和Fs2对输入信号进行采样，并将N（N＞I）个采样值用矢量表示如下

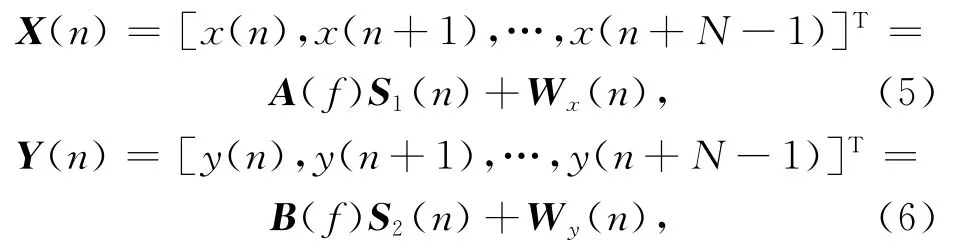
其中

其中，数字频率f1i=Fi／Fs1，f2i=Fi／Fs2各不相同，即l1i=mod（Fi／Fs1），l2i=mod（Fi／Fs2）各不相同，Wx（n），Wy（n）表示噪声向量.

采样序列的自相关矩阵为

式中：RS1=E［S1（n）SH1（n）］，RS2=E［S2（n）SH2（n）］，E［］表示期望运算，［］H表示共轭转置，δ2x，δ2y为噪声功率，I表示单位矩阵.对矩阵RXX和RYY特征值分解得到N个特征值，其中较大的I个特征值作为对角矩阵ΔS和ΩS的对角线元素，相应的特征向量ui和vi组成矩阵US=［u1，u2，…，uI］和VS=［v1，v2，…，vI］，N-I个较小特征值对应的特征向量ui和vi组成矩阵UN和VN.

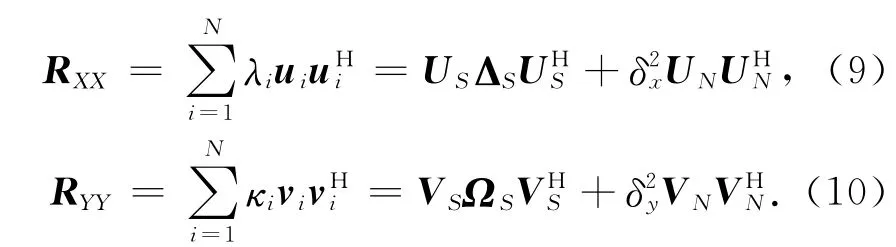
利用特征子空间理论［9］，US，VS张成的信号子空间正交于UN，VN张成的噪声子空间.有span（A（f））=span（US）⊥span（UN），span（B（f））=span（VS）⊥span（VN），联 合MUSIC谱函数表示为

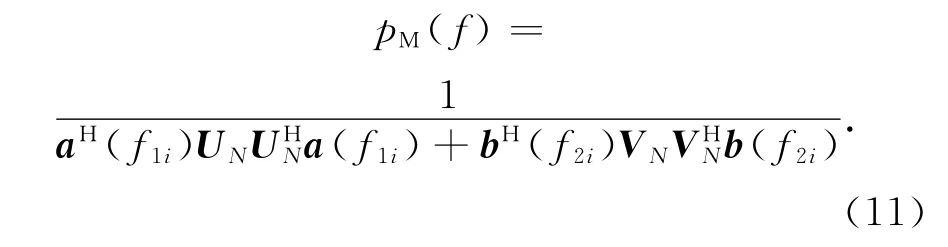
当a（f1i）和b（f2i）分别位于信 号子空 间span（US）和span（VS）时，必然存在a（f1i）⊥span（UN）和b（f2i）⊥span（VN），则aH（f1i）UN和bH（f2i）VN趋于零，联合MUSIC谱在信号频率Fi处会出现大的峰值，而在交调信号频率处联合MUSIC谱分布较平坦或者峰值较小.

2 频率搜索区间确定

由CCS无法直接实现对信号频率估计，存在判断谱峰的真伪性问题，利用联合MUSIC谱在每个CCS峰附近搜索可有效解决真伪峰的问题，因此确定频率搜索区间就成了关键，此方法不仅可以准确定位信号频率位置，还在降低MUSIC谱搜索量的同时实现了频率的高精度估计.

在非整数倍周期位置截断信号会导致频谱泄漏，假设某个信号的CCS峰位于DFT频率ki处，由于频谱泄漏，相邻频率ki+1或ki-1处CCS值也较大，因此信号频率一定是位于ki～ki+1或ki-1～ki之间，频率搜索区间选为

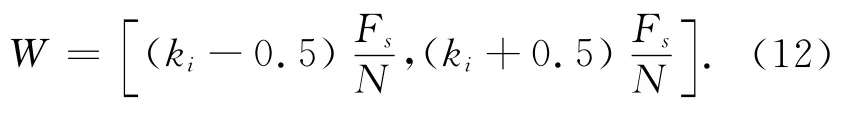
根据测频精度选择搜索步长Δf≪Fs／N，以Δf为步长，以谱峰位置ki为中心向两端扩展搜索［10］，直到满足式（13）和式（14），搜索停止.

式中：m=0，1，…，Fs／（NΔf）.联合MUSIC谱的频率估计均方根误差为

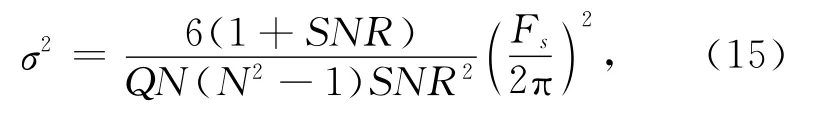
式中：σ为搜索误差；Q为信号采集周期数.

3 计算机仿真

假设输入频率分别为310 MHz和430 MHz的两个信号的混合信号，对该信号以200 MHz和250 MHz速率分别进行采样，由于不满足采样定理，采样信号频谱会出现混叠，信号采集周期数Q=100，每个周期采样点数N=128，联合MUSIC谱搜索步长取为0.2 MHz.两个欠采样序列的CCS如图1所示，4个谱峰中有2个对应信号频率，剩余2个对应交调信号频率.

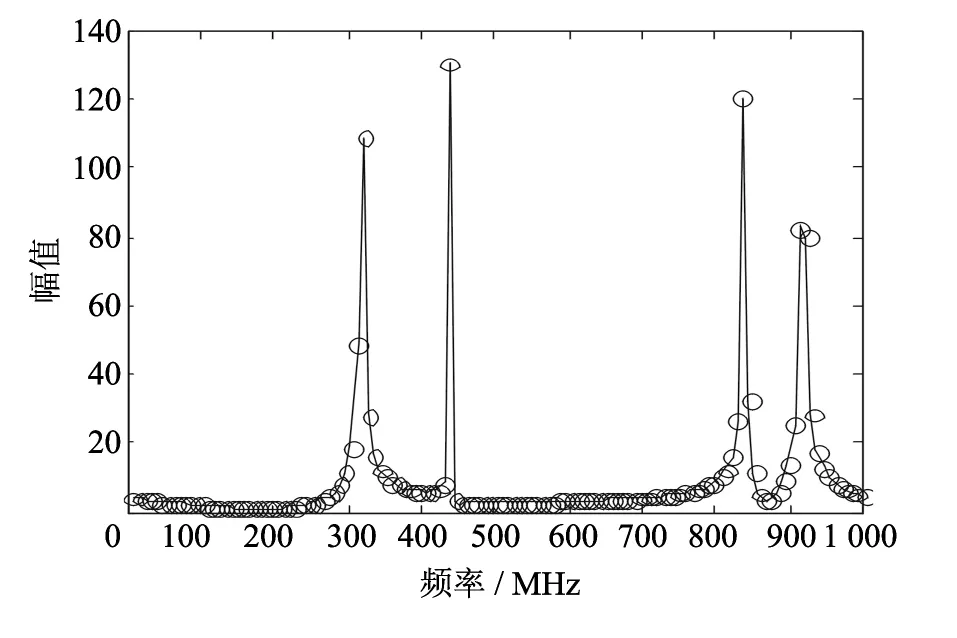
图1 互相关频谱图 Fig.1 Cross correlation spectrogram

两个采样序列在4个CCS峰处的MUSIC谱如图2和图3所示.由图2可知，以200 MHz速率采样得到的采样序列1的MUSIC谱在310，430，830，910 MHz这4个互谱峰处都出现了峰值，以250 MHz速率采样得到的采样序列2的MUSIC谱只在频率为310 MHz和430 MHz两处出现峰值，结合两个采样序列的MUSIC谱图，选择两者均在同一互谱峰频率处出现MUSIC谱峰的次数，就可以确定信号个数为2个，频率分别为310 MHz和430 MHz.

图2 采样序列1在互谱峰值附近的MUSIC谱 Fig.2 MUSIC spectrogram of sample sequence 1 in the neighbourhood of CSS peak

图3 采样序列2在互谱峰值附近的MUSIC谱图 Fig.3 MUSIC spectrogram of sample sequence 2 in the neighbourhood of CSS peak

图4（a）是SNR=10 dB时，仅频率为310 MHz的信号输入时的CCS图，由于满足|F1（T1-T2）|＜1，根据CCS的谱峰位置估计信号频率为312.5 MHz；对由速率为250 MHz的采样序列构造的MUSIC谱，在区间［310.55 MHz，314.45 MHz］内以步长为0.4 MHz，频率中心为312.5 MHz进行搜索，MUSIC谱图如图4（b）所示，根据MUSIC谱峰位置估计信号频率为310.2 MHz；其他参数不变，搜索步长改为0.2 MHz时的MUSIC谱分布图如图4（c），由谱峰估计信号频率为309.96 MHz，频率估计精度进一步提高.MATLAB仿真结果验证了本文方法，基于CCS的MUSIC谱搜索能够准确定位信号的模糊频率应在的频率区间，实现高精确测频.

图4 频谱图 Fig.4 Frequency spectrogram

4 结 论

针对宽带数字接收时的测频模糊问题，本文考虑到在同时多信号情况下利用不同速率的采样序列的CCS估计频率时存在交调信号频率影响，提出了CCS联合MUSIC谱的快速无模糊估计频率方法，根据CCS峰位置及测频精度要求选择搜索区间及步长，由MUSIC谱搜索结果就实现了信号频率估计，由于仅在有限个相关谱峰的邻近区间上进行搜索，搜索量不大，且频率估计精度较高.

［1］Ertan A E.Accurate single-tone frequency estimation from DFT coefficients using time-window＇s frequency spectrum［C］.IEEE Radar Conference，2013：1-6.

［2］王永良，陈辉，彭应宁，等.空间谱估计理论与算法［M］.北京：清华大学出版社，2005.

［3］Zhang J X，Christense M G，Jensen S H，et al.A robust and computationally efficient subspace-based fundamental frequency estimator［J］.IEEE Trans on Audio，Speech，and Language Processing，2010，18（3）：487-497.

［4］Baransky E，Itzhak G，Wagner N，et al.Sub-nyquist radar prototype：hardware and algorithm［J］.IEEE Transactions on Aerospace and Electronic Systems，2014，50（2）：809-822.

［5］余朋骏，阮怀林.迟延相位差结合FFT多信号频率估计［J］.电子信息对抗技术，2014，29（3）：7-12.Yu Pengjun，Ruan Huailin.The frequency estimation of multi signal based on delayed phase difference and FFT［J］.Electronic Information Warfare Technology，2014，29（3）：7-12.（in Chinese）

［6］Sarma A，Tufts D W.Rank-order adaptive CFAR：performance bounds and efficient implementation［J］.IEEE Transactions on Aerospace and Electronic Systems，2013，49（4）：2211-2224.

［7］王鑫，赵春晖，戎建刚.多路延迟结构的修正MUSIC算法频率估计［J］.系统工程与电子技术，2009，31（4）：795-798.Wang Xin，Zhao Chunhui，Rong Jiangang.Frequency estimation of modified MUSIC algorithm based on multi-path delay structure［J］.Systems Engineering and Electronics，2009，31（4）：795-798.（in Chinese）

［8］李鹏，朱平云，陈望达.欠采样信号多采样频率处理方法［J］.海军航空工程学院学报，2004，19（1）：165-167.Li Peng，Zhu Pingyun，Chen Wangda.Using different frequencies method to solve bandpass sub-nyquist sampling［J］.Journal of Naval Aeronautical，2004，19（1）：165-167.（in Chinese）

［9］Elasmi Ksibi R，Besbes H，Cherif S.Equivalent fullband implementation of subband subspace methods for frequency estimation Signals［C］.3rd International Conference on Circuits and Systems（SCS），2009：1-6.

［10］蒋毅，刘章文，古天祥.MUSIC法的有限域单向快速频率搜索［J］.电子科技大学学报，2008，37（2）：241-243.Jiang Yi，Liu Zhangwen，Gu Tianxiang.Fast frequency estimation way for MUSIC algorithm［J］.Journal of University of Electronic Science and Technology of China，2008，37（2）：241-243.（in Chinee）