企业债市场风险的度量——基于GARCH和半参数法的VaR 模型分析

■刘国鹏，彭淑娴

一、引言

近年来，随着经济全球化与信息科技的不断发展，金融国际化日趋增速，金融风险管理的作用越来越重要。各大跨国公司以及各国监管当局都投入大量精力、人力与财力研究开发风险管理技术。因此风险的度量以及分析技术发展得相当迅速，而且可以较快地转换成经济效益。债券是政府、金融机构、工商企业等机构直接向社会借债筹措资金时，向投资者发行，承诺按一定利率支付利息并按约定条件偿还本金的债权债务凭证。企业债券是有企业发行的债券，它是企业融资的重要手段，也是金融市场上的主要金融工具之一。在美国等西方证券市场发达的国家，企业债券市场是证券市场的重要组成部分，债券市场的规模甚至超过了股票市场的规模。近年来我国债券市场发展迅速，规模不断增加，但相比较而言，国债和金融债发展较快，企业债却始终止步不前。究其原因，政府债只具有利率风险，而企业债除了具有利率风险外还具有信用风险，政府主管部门对企业债风险的担心在相当大程度上限制了企业债的发展速度。因此，如何认识和揭示企业债的风险，成为影响我国企业债市场发展速度的一个关键因素。但是，到目前为止，国内学者在债券方面的研究不少，然而研究企业债风险问题的文献并不多，特别是用最新数据进行实证研究的文章几乎没有，这并不利于我国企业债市场的长远发展。通过最新的方法和数据度量企业债市场风险，对企业债市场健康发展具有十分重要的意义。

二、文献回顾

关于企业债券市场波动性，国外研究多集中在企业债券价格及变化率的影响因素方面。Vasiliki D.Skintzi和Apostolos N.Refenes（2006）对欧洲债券市场的动态联系进行研究，发现整个欧洲地区债券市场以及美国债券市场对欧洲单个国家的债券市场存在波动溢出效应。此外，欧元的引入加强了波动溢出效应以及大部分欧洲债券市场之间的交叉关联。Tim Bollerslev、Jun Cai和Frank M.Song(2000)对美国国库券市场进行研究发现公开信息是盘中波动水平的重要来源。

国内的相关研究主要有寇宣兵、吴浪霞（2008）采用STR 方法来分析股票和债券之间的联动关系，发现所选的样本中，企业债券收益具有明显的波动非对称性，而相关联的股票收益非对称波动在样本区间不明显。林娟、杨凌(2007)对银行间债券市场7天回购利率进行研究，结果显示7 天回购利率呈现右偏、厚尾和非正态的分布形态。波动具有集群性、持久性且呈现出均值回复现象。徐小华(2006)等用STAR-ARCH 模型和EGARCH 模型来检验交易所和银行间债券市场杠杆效应存在情况，发现交易所债券市场价格波动中存在明显的杠杆效应，而银行间市场却不存在，这说明两个债券市场对不同的政策干预和信息冲击具有不同程度的反应。

虽然对中国债券市场的研究文献较多，但是涉及企债市场风险大小度量的文献却少之又少。我国企业债未来将发展迅速，规模会大幅增加，相应地，企业债券市场的风险研究也将为之重要。我们必选建立一套合理的风险度量体系，来管理和控制企业债券的市场风险。本文在分析和总结已有研究结果的基础上，用基于GARCH和半参数法的VaR 模型对企业债市场收益率序列建模，研究了企业债市场的波动特点，以期较好地对企业债市场风险进行度量。

三、理论介绍

（一）VaR 理论

1.VaR 定义

VaR 是风险估值模型(Value At Risk)的简称，是近年来国外兴起的一种金融风险管理工具，旨在估计给定金融产品或组合在未来资产价格波动下可能的或潜在的损失。用Jorion(1996)给出的权威定义，可将其表述为：给定置信区间的一个持有期内的最坏的预期损失0，即在一定的持有期和一定的置信度内，某金融工具和投资组合所面临的潜在的最大损失金额。假设给定的置信水平为1-σ，资产或资产组合在持有期内的损失为△P，则VaR 的定义可以表示为式（1）所示：

2.VaR 计算的参数方法

在不对分布作出假设、最一般的情况下，为计算一投资组合中的VaR 定义W0为初始投资额，R 为投资收益率，预期收益率为μ，波动性为σ，一定置信水平1-σ 下的最小收益率为R*，持有期末投资组合的价值和最小投资价值分别为W=W0（1+R）和W*=E（W）-W0（μ-R*），则VaR 的计算如式（2）所示：

从式（2）可知，只要知道资产组合的最小投资价值w*或最小投资收益率R*，就可以计算得到VaR。而W*和R*可以通过式（3）计算得到：

式（3）中的f（w）和f（r）分别为投资组合价值和投资收益率的概率分布。

根据是否对收益率的分布作出假设，VaR 的计算方法可以分为三类：参数方法（亦称方差—协方差方法）、非参数方法（包括历史模拟法和蒙特卡罗模拟法）、半参数方法。本文拟采用参数法、半参法数计算VaR，参数方法是指假设收益率服从某一分布，如正态分布，然后根据这一分布的统计特征，如期望、方差，计算VaR。然而，金融数据通常具有尖峰、厚尾特征，因此，本文假设收益率服从广义误差分布（GED）来计算VaR。广义误差分布下VaR 的计算公式如式（4）所示：

式（4）中，Zα为广义误差分布下置信水平为α对应的下分位数，pt-1为前一日的企债价格指数，ht为收益率的条件方差。从（4）式可以看出，VaR 的计算取决于四个参数：（1）前期收益率价格；（2）置信水平α；（3）资产收益的分布设定；（4）收益的方差。资产收益的分布本文设定为广义误差分布，收益的方差用GARCH 族模型可以计算得到，置信水平的选择则没有什么可遵循的规则，置信水平越高，意味着VaR 的数值越高，在本文的实证分析中拟选择95%的置信水平。

3.VaR 计算的半参数方法

一些实证研究表明许多金融时间序列的收益率并不服从正态分布，而是具有尖峰厚尾的特征，在正态分布假设下计算得到的VaR 偏低，从而会低估实际风险。David X.Li(1999)提出的半参数法不需要做任何分布假设，只要计算收益率序列{r}的偏度、峰度、均值和方差，即可构造VaR置信区间上限和下限。假设收益率r 为随机变量，其均值、方差、峰度分别 为：和γ2=

若γ1=γ2=0，则X 服从N（μ，σ2）。计算收益率r的VaR 值可以按方差、协方差方法计算。若γ1≠0，γ2≠0，则r 不服从正态分布，可以证明，VaR 的置信上限和置信下限可以用下面的公式计算得到。

其中，γ1≠0，Zα为显著性标准，即为标准正态分布中α 对应的分位点。

（二）GARCH 模型

计算VaR 的方法有参数方法和非参数方法，其中参数方法在实践中被广泛应用。最早计算VaR 的参数方法是假设收益率服从某一特定分布（通常为正态分布），然后根据这一分布的统计特征计算VaR。这类方法是静态的参数方法，有比较大的缺陷。由于金融时间序列往往存在异方差现象和波动聚集性特征，用静态的分布特征不足以刻画这一特点，而GARCH 模型是反映市场时变特征最为常用的波动率模型，能有效地捕捉资产收益率波动的聚类和异方差现象。

（三）广义误差分布（GED）

运用GARCH 模型时需要考虑残差序列{εt}的特征，通常假定其条件分布为标准正态分布，但由于收益率序列通常具有尖峰厚尾特征，该假定会导致金融资产风险的估计出现较大的误差。如果假设残差的条件分布服从t 分布和广义误差分布（GED），则可以描述收益率序列的尖峰厚尾特征。而广义误差分布（GED）是一种更为灵活的分布形式，也是一种处理厚尾的方法。其优点在于通过对其中的参数v的调整变化可以拟合不同的分布形式，正态分布只是其中的一个特例。其密度函数形式如下：

我们可以通过令参数v=1、2和3 分别得到其密度分布函数来考察广义误差分布处理厚尾的能力。如下图（图1 为密度函数对比图，图2 为左尾放大对比图）：

图1 不同参数的广义误差分布

图2 不同参数广义误差分布尾部对比图

四、模型的建立与评价

（一）变量构造与数据选取

企债指数在2003年6 月9 日正式发布，填补了交易所企业债券指数的空白，为衡量企业债券市场整体风险收益提供了一个标尺。企债指数直观表征交易所企业债券市场的运行状况，不仅有利于提高投资者投资效率，更是为机构投资者指数产品创新拓展了空间。我们选取了2003年6 月9 日到2013年4 月29 日为样本时期，共2471 个样本，以上证企债指数为分析对象，数据来源于大智慧终端。在这里我们对收益率的计算采用如下的公式：

其中pt是企债指数的日收盘价。本文数据处理与分析采用软件为Eviews和R。

（二）基本统计分析与平稳性检验

上证企债收益率rt序列时序图如图3 所示，从图3 可以看出收益率序列存在明显的波动集群现象，即大的波动后面紧跟着另一个大的波动，小的波动后面紧跟着另一个小的波动。由表1 的基本统计分析可知，企业债指数的收益率序列的偏度系数小于0、峰度系数大于0，表明我国企业债市场收益率分布为左偏分布，且具有明显的尖峰特征，由JB 统计量P 值为0 也说明rt并非正态分布。从图4 rt的QQ 正态分布图可以看出，rt上端右偏离直线，向下倾斜，下端左偏离直线,向上翘起，这说明rt上尾和下尾都具有明显的厚尾行，用正态分布来模拟企业债券市场收益率的变化是不合理的。

图4 收益率序QQ 图

表1 我国企业债指数市场价格日收益率序列的基本统计特征

（三）收益率序列平稳性检验

收益率序列平稳性检验多用ADF 单位根检验法，检验结果如表2 所示，在1%显著性水平下，收益率序列rt是平稳的。

表2 rt平稳性的ADF 单位根检验结果

（四）收益率序列ARCH 效应检验

建立GARCH 模型计算VaR 的方差-协方差模型首先要进行企业债券收益率序列的异方差性（ARCH）检验，我们利用Eviews，采用残差自相关检验和拉格朗日乘数检验方法，得到表3 的检验结果。

表3 企业债指数收益率序列的异方差性检验

从上表3 可以看出，企业债指数收益率序列的滞后1-12 阶大于统计量Q和LM 的概率都远远小于0.01，这表明上证综合指数收益率序列存在明显的异方差性，并且误差方差随时间而变化，为了从变化的误差方差中提取有用信息，可以建立广义自回归条件异方差模型（GARCH）。

（五）模型建立

考虑到企业债券市场资金量是影响企债收益率的重要因素，我们以企业债券市场成交额变化率为自变量（记为x，x=，lt和lt-1分别为当前和上期的成交额），同时为了能够反映出收益率的日历效应，用企业债券收益率r和成交额变化率x 及其之后若干期变量分别建立在假设εt服从广义误差分布（GED）的GARCH(1，1)、GARCH(1，1)-M、EGARCH(1，1)模型。经过变量筛选和三种模型的参数、各种统计检验值的比较，我们认为GARCH(1，1)-M 模型效果比较理想，其模型的表达、模型参数和各种检验统计量见表4。

根据上面所建立的GARCH (1，1)-M 模型计算得到ht，将其代入公式（4），计算得到企业债券市场每日的VaR 值，该值给出了企业债券市场价格指数在某一置信概率下的最大损失下界，估计的结果分别见表5、表6：

表4 企债指数收益率序列GARCH(1，1)-M 模型的参数估计结果

表5 基于GARCH(1，1)-M 模型的最大前十名VaR 值和条件异方差ht 值

表6 基于GARCH(1，1)-M 模型的VaR 值和条件异方差ht 值的基本统计特征

（六）基于David X，Li（1999）半参数的估计

同样使用2003年6 月9 日到2013年4 月29日企债指数的日收益率数据，计算出企业债市场收益率的偏度γ1和峰度γ2，结果显示γ1和γ2显著不为0，同时结合QQ 图判定我们假设正态分布的假设有失妥当。采用公式（5）、（6）计算得到VaR 的置信上限和置信下限，结果见表7

表7 企债指数基于半参数的VaR 值

（七）用似然比检验对实证模型进行评价

通过表8 中的VaR 预测失败频率一行可以看出，GARCH (1，1)-M和半参数法的失败频率分别为4.47%和4.23%，均小于相应的显著性水平5%。单从失败频率上看，半参数法最小，但是其预测结果是否可信，则需要进一步的检验，本文使用Kupiec(1995)的LR 统计量检验。Kupiec 认为对VaR 值的估计是独立事件，如果实际损失小于VaR 值，则视为一个成功的事件，如果实际损失大于VaR 值，则视为一个失败的事件。Kupiec 给出了零假设一失败频率与估计VaR 值的左尾概率无显著性差异，这样，对VaR 模型精度的检验就转化为检验失败频率是否显著不同于显著性水平。

Kupiec 给出了零假设的似然比率检验统计量：

其中，P 为显著性水平，1-P 为置信水平，T 为样本容量，N 为失败次数，即实际损失大于VaR 值的次数。LR 服从自由度为1 的X2分布。检验95%置信水平下的LR 值结果见表8。从中可以看出，在95%的置信水平下，GARCH(1，1)-M和半参数法的LR 统计量均小于相应的X2（1）临界值，因此不能拒绝零假设，即失败频率与估计VaR 值的左尾概率无显著性差异因此拒绝零假设，即失败频率异于估计VaR值的左尾概率，两种模型都通过检验。

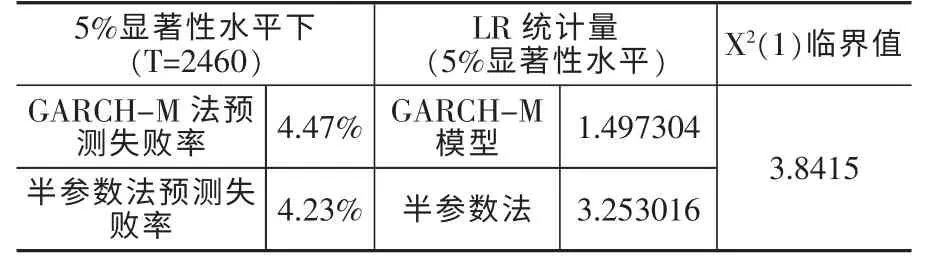
表8 VaR 预测失败频率及LR 统计量检验结果

五、实证结果分析与结论

现在我们对模型评估结果进行实证分析。由表5 可以看出，上证企债最大前十名VaR 值集中在2004年4 月（22 日），2008年9 月（18、19 日），2008年10 月（9、10、13、14、15、16、21 日），说明这些时间上投资者面临债指下跌的潜在风险较大。其中，上证企债在2008年10 月14 日VaR 值最大，为1.5 点，说明在95% 的置信概率下未来上证企债指数可能最大下跌1.5 点（1.16%），这对于相对安全的债市来讲，已经是相当大的风险了。我国债市在这些时间上风险极大的主要成因来源于宏观经济风险和政策风险，如2004年4 月的极大风险的形成主要是市场极强的加息预期和央行整治债市引起的；2008年9月、10 月的极大风险主要源于美国的次债危机波及我国，引起市场极大恐慌。从表6 所列上证企债VaR 的基本统计量可以看出，上证企债VaR 序列的偏度小于0、峰度大于0，表明该序列与标准正态分布有一定偏离，具有左偏、高峰特征，说明在企业债的日VaR 值中，低于按其自身时间序列计算的平均VaR 值天数较多。平均来看，深市平均每日VaR 值为0.26 点（平均0.22%），说明上证企债市场风险相对较小，上证企债投资者面临的指数下跌的潜在风险较小。综上，就企债市场而言，风险相对较小，但不排除特殊时期风险很大，如上证企债在2008年10月14 日面临下跌1.16%的潜在风险，这相对平均0.22%的潜在下跌风险已相当大了。

通过以上实证分析，我们可以得到如下结论：

（一）基于GARCH-M 模型计算得到的VaR 值以债指未来每日可能下跌的最大点数描述了市场绝对风险的大小，而基于半参数法得到的VaR 值以市场收益率未来每日可能下跌的最大速率描述了市场相对风险的大小，因而两种模型是可以配合使用的，并且配合使用的两种模型能对债券市场风险很好的刻画。

（二）我国债券市场风险与收益存在正相关关系，市场风险是影响市场收益的一个重要显著性因素，这可以从所建立的GARCH-M 模型中的参数显著为正（见表4）得到证明。因而，现阶段我们对债券收益率建模分析时，市场风险这个因素不可忽视。

（三）就绝对风险而言，和股票基金等相比，企业债是风险相对小的证券；但值得注意的是，就相对风险而言，企业债所存在的风险还是值得注意的，如2008年10 月14 日可能下跌1.16%。

另外，目前我国企债市场逐渐走向成熟，特别是随着利率自由化的不断发展，债市市场化也会加速，无论对投资者还是政策制定者而言，债市风险应当更加受到关注。

[1]Vasiliki D.Skintzi，Apostolos N.Refenes.Volatility spillovers and dynamic correlation in European bond markets.Journal of International Financial Markets，Institutions and Money，2006，Volume 16，23～40.

[2]Tim Bollerslev，Jun Cai，Frank M.Song.Intraday periodicity，long memory volatility，and macroeconomic announcement effects in the US Treasury bond market.Journal of Empirical Finance，2007，Volume 7，37～55.

[3]寇宣兵，吴浪霞.企业债券与相关联公司股票价格波动的非对称性研究[J].中国商界，2008，（6）：7～9.

[4]林娟，杨凌.银行间债券市场7 天回购利率波动性分析[J].福州大学学报，2007，（2）：45～47.

[5]徐小华，何佳，吴冲锋.我国债券市场价格非对称性波动研究[J].金融研究，2006，（12）：14～22.