岩体抗剪强度参数对边坡安全系数的敏感性分析

张东旭，侯克鹏，杨志全，杜　俊

（1.昆明理工大学 国土资源工程学院，云南 昆明 650093；2.昆明学院 城乡建设与工程管理学院，云南 昆明 650412）

岩体抗剪强度参数对边坡安全系数的敏感性分析

张东旭1，侯克鹏1，杨志全1，杜俊2

（1.昆明理工大学 国土资源工程学院，云南 昆明 650093；2.昆明学院 城乡建设与工程管理学院，云南 昆明 650412）

云南某露天边坡岩体主要以大理岩化灰岩为主，边坡岩体整体呈中风化，随着后续开采，边坡的安全问题将制约矿山的发展。黏聚力（c）和内摩擦角（φ）是影响边坡工程和地下工程稳定性的主要因素，研究通过多种方法获得岩体力学参数，对比了由Hoek-Brown强度准则和岩体直剪试验得出的岩体参数，使用敏感性分析理论分析了内摩擦角和黏聚力对某露天矿岩质边坡的安全系数的影响。结果表明，Hoek-Brown强度准则得出的岩体抗剪强度参数比较可靠；在黏聚力和内摩擦角取值较小时，对安全系数的敏感性差异不明显，当二者取值较大时，以2%参数变化率为临界点，内摩擦角对岩质边坡的稳定性更显著。

边坡；岩体力学参数；岩体直剪试验；安全系数；敏感性

云南某露天矿边坡岩体主要以大理岩化灰岩为主，边坡岩体整体呈中风化，边坡顶部覆盖少量第四系黄土。地形为中部高，两边低，目前边坡高度160m。由于边坡中部矿体褶皱发育且岩性较差，边坡中部已有两个楔形滑坡，随着后续开采，边坡将继续增高，边坡的安全问题将制约矿山的发展。根据吴胜仓[1]对岩体参数对边坡稳定性影响的研究，黏聚力和内摩擦角是边坡稳定性的控制因素。邓左民等[2]在某钨矿开采稳定性的三维有限元分析中指出围岩应力是影响矿山稳定性的主要因素，说明了岩体抗剪强度的重要，所以有必要进行岩体抗剪强度参数对岩质边坡的敏感性分析。敏感性分析的核心目的就是通过对模型的属性进行分析，得到各属性敏感性系数的大小[3]。文章采用敏感性分析方法，探讨抗剪强度参数对边坡稳定性的影响，在实际应用中根据经验去掉敏感性系数很小的属性，重点考虑敏感性系数较大的属性。

目前，敏感性分析的方法大致分为三类：一是每次计算中仅变化某一变量，分析边坡安全系数对其的敏感性[4]；二是采用正交设计、均匀设计、BP神经网络等方法进行多因素分析[5-7]；三是谭晓慧[8-9]等人使用的可靠度法分析边坡稳定性敏感性分析，吴振君等[10]在可靠度分析基础上，采用随机场模型来描述边坡滑面上岩土参数的空间变异性，提出了新的可靠度分析方法。文章采用第一类敏感性分析方法研究，分析了大理岩化灰岩强度参数对边坡安全系数的敏感性的规律，可用以指导此岩质边坡的岩体参数选取。

1　岩体参数的选取

研究边坡稳定性时，岩体参数的选取至关重要。故使用两类方法获取其岩体抗剪强度参数：一是经验强度准则，使用广义Hoek-Brown强度准则[11]，准则为：

式中：σ1、σ3分别是岩体破坏时的最大和最小主应力，MPa；σci为岩块的单轴抗压强度，MPa；mi为岩石量纲一的经验参数，反映岩石的软硬程度；mb，s，a为反映岩体特征的经验参数，D为扰动系数；GSI为地质强度指标。

根据 Hoek于 2002年提出了等效 Mohr-Coulomb准则参数c、φ的确定式[11]：

式中：σ3n=σ3max/σci；σ3max的确定，在边坡工程中Hoek给出如下经验公式：

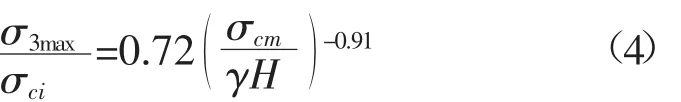
式中：γ为岩体的容重，g/cm3；H为边坡高度，m；σcm为节理岩体的整体强度，MPa。可由等效的Mohr-Coulomb强度参数确定：

具体计算时根据现场调查和室内试验，此岩质边坡大理化灰岩容重为2.66g/cm3，确定σci=68MPa，D=1，GSI=38，mi=11，由式（3）~（5）进行迭代计算求解。

二是进行现场直剪试验，针对大理岩化灰岩共进行2个试坑，10个试体。在对现场直剪试验数据分析时，分别采用最小二乘法、随机-模糊法和可靠度法进行线性回归，求出岩体抗剪强度指标，见表1。

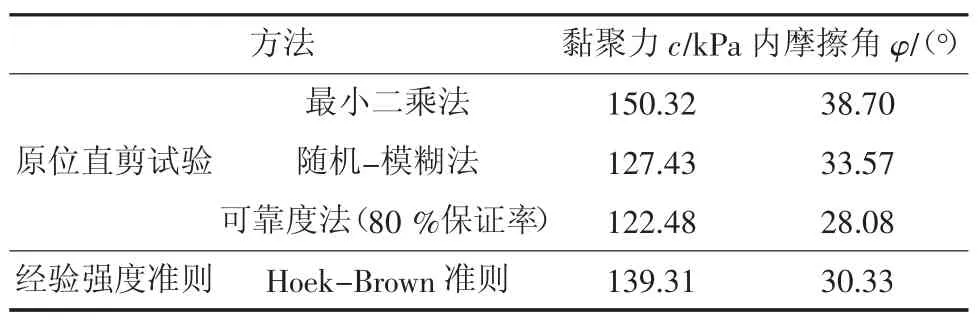
表1　大理化灰岩抗剪强度参数值Tab.1　Shear strength parameter ofm arbleized limestone

由表1可见，不同方法得到的岩体强度参数差异较大。

取原位直剪试验三种数据分析方法的平均值作为直剪试验得出的岩体参数，与Hoek-Brown准则得出的岩体参数进行比较，见表2。由表2可见Hoek-Brown准则估算的岩体抗剪参数与原位直剪试验的试验值接近，根据宋彦辉等[12]的研究，在实际法向应力较低的情况下，用Hoek-Brown准则估算的结果将导致c值偏大而φ值偏小，本次Hoek-Brown准则估算的结果验证了该结论。

为分析黏聚力和内摩擦角对边坡安全系数的影响，将黏聚力和内摩擦角从最小值到最大值五等分，见表3，计算边坡安全系数时使用不同的黏聚力和内摩擦角组合进行计算。

表2　原位直剪试验与Hoek-Brown准则得出岩体抗剪强度参数比较Tab.2　Com parison of shear strength param eter using rockmass direct shear testand Hoek-Brown failure criterion

表3　抗剪强度参数等分表Tab.3　Equal tab leof shear strength param eter

2　边坡模型的选取

根据郑颖人[13]的观点，当坡脚到左端边界的距离为坡高的1.5倍，坡顶到右端边界的距离是坡高的2.5倍，并且上下两边界距离不小于2倍坡高时，计算的精度比较合理，最终使用边坡模型的尺寸如图1所示。

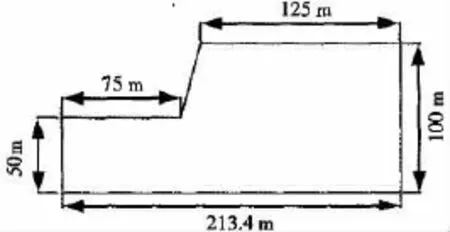
图1　岩质边坡计算模型尺寸Fig.1　M odelsizeof rock slope

3　敏感性分析

在对模型进行稳定性计算时，使用Slide软件，为避免不同算法对计算安全系数的影响，采用边坡稳定性分析常用的简化Bishop算法，见式（6），将表3参数进行不同组合进行边坡稳定性计算，得出的边坡稳定性系数见表4。不同的黏聚力和不同的内摩擦角组合计算得出的安全系数的关系见下图2，图3。

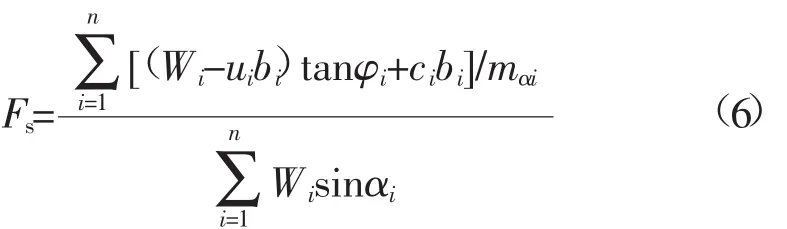
式中：mαi=cosαi+sinαitanφi/Fs，Fs为安全系数，Wi为第i条块体重力，N；ui为条底孔隙水压力，Pa；bi为条块宽度，m；φi为滑面内摩擦角，（°）；ci为黏聚力，Pa；αi为底面倾角，（°）。

由图2可以看出，内摩擦角取一定值时，安全系数与黏聚力大致呈现线性关系，内摩擦角相同时，黏聚力越大，安全系数也越大。图3中，黏聚力取一定值时，安全系数与内摩擦角也大致呈线性关系，黏聚力相同时，内摩擦角越大，安全系数也越大。

敏感性分析是系统分析稳定性的一种方法[14]。设有一结构系统，其系统特性P由n个因素α={α1，α2，…，αn}决定，系统模型设为P=f{α1，α2，…，αn}。在某一基准态α*={α1*，α2*，…，αn*}下，系统特性为P*。分别令各因素在其各自的范围内变动，由于这些因素的变动，系统特性P偏离基准状态，P*的趋势和程度，这种分析方法称为敏感性分析[15]。

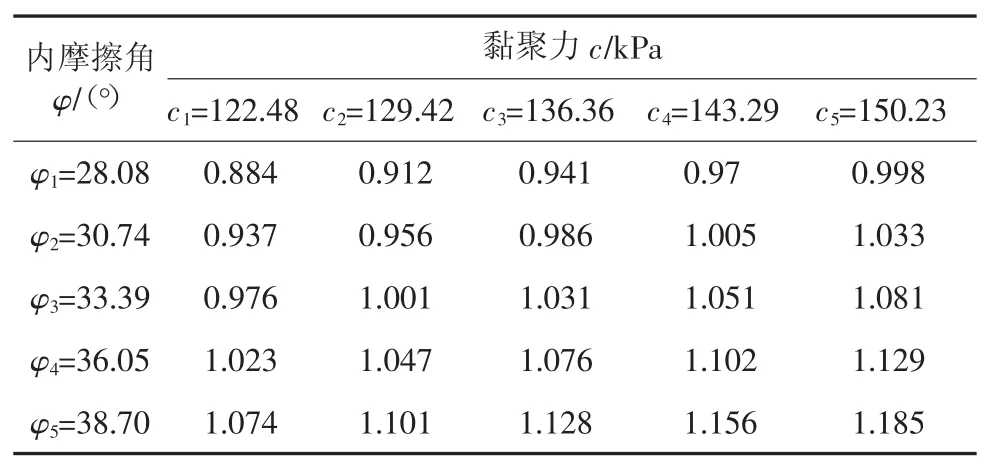
表4　安全系数计算表Tab.4　Tableof safety factor

图2　黏聚力与安全系数关系Fig.2　Relationship between cohesion and safety factor

图3　内摩擦角与安全系数关系Fig.3　Relationship between internal friction angleand safety factor

为了分析岩体的黏聚力和内摩擦角对边坡安全系数的敏感性，需要选取基准参数计算安全系数的基准值，图2和图3均表明当内摩擦角或者黏聚力固定时，其对应的黏聚力或内摩擦角对安全系数呈现线性关系，因此可选其中一组参数进行分析，此处选取内摩擦角和黏聚力的平均值（c3=136.36 kPa，φ3=33.39°）作为基准值，计算出的安全系数值作为基准数值。然后分别计算黏聚力和内摩擦角变化时的安全系数变化率，结果见表5，并绘制成图4。从图4可知，内摩擦角与黏聚力取较大值时，内摩擦角对安全系数的敏感性大于黏聚力对安全系数的敏感性，当两个参数取较小值时，内摩擦角对安全系数的敏感性与黏聚力对安全系数的敏感性趋于一致，二者对安全系数的影响区别表现不明显。陈鹏等[16]对岩质边坡的因素敏感性对边坡稳定性可靠度分析影响的研究，得出内摩擦角的敏感性大于黏聚力的敏感性的结论，此结果与本研究成果不一致，原因是其选取的因素变化率较小，为10%~20%，且各因素变化幅值不一致，最终导致当两个参数敏感性分析结论有误。而根据牛岩，鲍小成等[17]用灰色关联分析法对排土场边坡的敏感性分析，得出了黏聚力的敏感性大于摩擦角的结论，这是因为岩石和土的差异性引起的，物理性质差异很大程度上决定了力学性质的差异，最终导致分析结果的差异。

表5　参数变化对安全系数的变化率　%Tab.5　Change rateof safety factor to param eters change

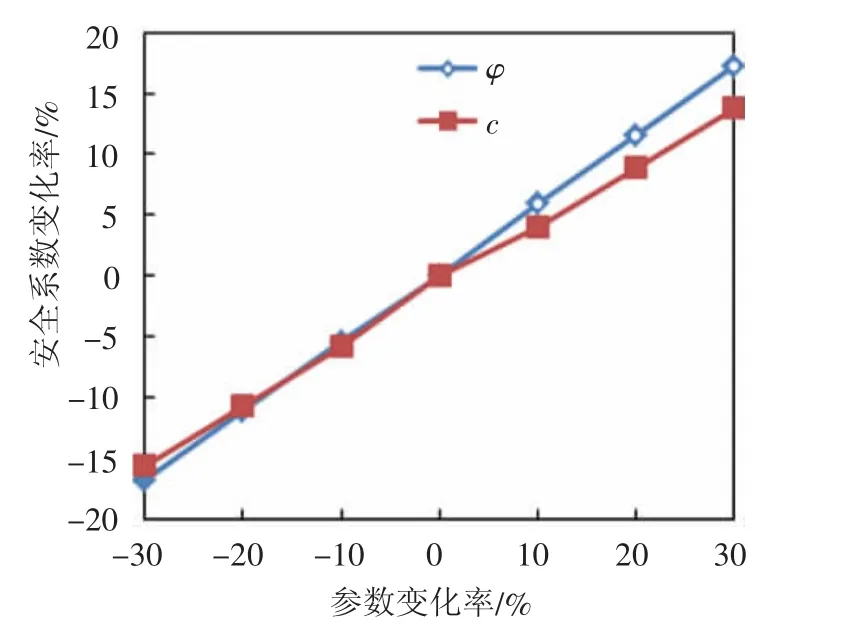
图4　参数变化与安全系数的关系Fig.4　Relation between varying parametersand safety factor

由图4可知当黏聚力和内摩擦角两个参数变化范围在-20%~0%时，安全系数的变化率趋于一致，此处取的黏聚力和内摩擦角值的最小值对平均值的变化率分别为-10.18%和-15.90%，在-20%~0%范围内，表明大理岩化灰岩的岩体抗剪参数在减小时对安全系数的变化率趋于一致。本文选取的黏聚力和内摩擦角的最大值对平均值的变化率分别为10.18%和15.9%，为了分析参数在此范围变化对安全系数的变化率，并找出两个参数变化率对于安全系数影响产生差异的临界点，设定参数最大变化率为15%，并使用上面的计算方法详细计算参数对安全系数的敏感性，结果见表6，并绘制成图5。

表6　参数变化对安全系数的变化率细表　%Tab.6　Specific change rateofsafety factor to parameterschange

图5　参数与安全系数的关系细化图Fig.5　Specific change relation between param etersand safety factor

分析图5可见，当参数变化率为1%时，两个参数变化对安全系数的变化率相差小于1%，当参数变化率为2%时，两个参数变化对安全系数的变化率相差略大于1%，因此可将参数变化率2%作为临界点，过了此点后参数变化对安全系数的变化率差异明显，即内摩擦角对边坡安全系数的敏感性明显大于黏聚力对边坡安全系数的敏感性。综合分析图4和图5，当安全系数的变化率在±5%范围内时，两个参数的变化率约在平均值±10%的范围。由此可知岩体抗剪强度参数的选取范围应该控制在平均值的±10%之内时，计算出的安全系数才比较可靠。

根据本文分析的岩体参数对安全系数的影响规律，黏聚力偏大导致安全系数的增大，内摩擦角偏小将导致安全系数减小，由此计算出的安全系数偏离实际值的程度由黏聚力与内摩擦角偏离实际值的程度共同决定，用Hoek-Brown准则估算的岩体抗剪参数计算边坡安全系数最终趋近安全系数的实际值。

4　结论

通过改变大理岩化灰岩的岩体抗剪强度力学参数，对模型计算边坡安全系数，并运用敏感性分析理论分析岩体抗剪强度力学参数对边坡安全系数的影响，得出结论如下：

（1）大理岩化灰岩的黏聚力和内摩擦角二者中任一值取定值时，边坡安全系数与另一值大致呈现线性递增关系。

（2）大理岩化灰岩的黏聚力和内摩擦角对边坡安全系数的敏感性关系为：两个参数较大时，内摩擦角对安全系数的敏感性更大，当两个参数较小时，两个参数敏感性趋于一致。

（3）参数变化率2%是大理岩化灰岩的黏聚力和内摩擦角两个参数对安全系数敏感性表现出明显差异的临界点，过了此点内摩擦角对安全系数更敏感。

（4）Hoek-Brown准则估算的岩体抗剪参数与原位直剪试验的试验值较为接近，但是仍需调整。参考文献：

[1]吴胜仓.岩体参数对边坡稳定性影响敏感性分析[D].北京：中国地质大学，2012.

[2]邓左民，李春.某钨矿69#矿体开采稳定性的三维有限元分析[J].中国钨业，2013，28（2）：14-17. DENG Zuo-min，LIChun.3D finite elementanalysison themining stability of a tungsten Mine's 69#orebody[J].China Tunsten Industry，2013，28（2）：14-17.

[3]蔡毅，邢岩，胡丹.敏感性分析综述[J].北京师范大学学报：自然科学版，2008，44（1）：9-15. CAI Yi，XING Yan，HU Dan.On sensitity analysis[J].Journal of Beijing NormalUniversity：Natural Science，2008，44（1）：9-15.

[4]张少宏.黄土边坡稳定计算中参数的敏感性分析[J].水利与建筑工程学报，2003，1（3）：40-42. ZHANGShao-hong.Analysisofsensitivity of parameter in stability calculation of loess slope[J].Journal of Water Resources and ArchitecturalEngineering，2003，1（3）：40-42.

[5]倪恒，刘佑荣，龙治国.正交设计在滑坡敏感性分析中的应用[J].岩石力学与工程学报，2002，21（7）：989-992. NIHeng，LIUYou-rong，LONGZhi-guo.Applicationsoforthogonaldesign to sensitivity analysis of landslide[J].Chinese Journal of Rock Mechanicsand Engineering，2002，21（7）：989-992.

[6]陈高峰，程圣国，卢应发，等.基于均匀设计的边坡稳定性敏感性分析[J].水利学报，2007，37（11）：1397-1401. CHENGao-feng，CHENGSheng-guo，LUYing-fa，et al. Sensitivity analysis of slope stability based on uniform design[J]. JournalofHydraulic Engineering，2007，37（11）：1397-1401.

[7]夏元友，熊海丰.边坡稳定性影响因素敏感性人工神经网络分析[J].岩石力学与工程学报，2004，23（16）：2703-2707. XIA Yuan-you，XIONG Hai-feng.Sensibility analysis of slope stability based onartificial neural network[J].Chinese Journal of Rock Mechanicsand Engineering，2004，23（16）：2703-2707.

[8]谭晓慧，王建国，刘新荣，等.边坡稳定的有限元可靠度计算及敏感性分析[J].岩石力学与工程学报，2007，26（1）：115-122. TAN Xiao-hui，WANG Jian-guo，LIU Xin-rong，et al.Finite element reliability computation and sensitivity analysis of slope stability[J].Chinese Journalof Rock Mechanicsand Engineering，2007，26（1）：115-122.

[9]EL-RAMLYH，MORGENSTERNNR，CRUDENDM.Probabilistic stability analysis of a tailings dyke on pre-sheared clay shale[J]. Canadian Geotechnical Journal，2003，40（1）：192-208.

[10]吴振君，王水林，汤华，等.一种新的边坡稳定性因素敏感性分析方法.[J].岩石力学与工程学报，2010，29（10）：2050-2055. WU Zhen-jun，WANGShui-lin，TANGHua，etal.A new sensitivity analysisapporach for slope stability—reliablity analysismethod[J]. Chinese Journal of Rock Mechanics and Engineering，2010，29（10）：2050-2055.

[11]HOEK E，CARRANZA-TORRESC，CORKUM B.Hoek-Brown failure criterion-2002 edition[C]//HAMMAH R，BAWDENW F，CURRAN J，et al.Proceedings of the North American Rock Mechanics Society NARMS-TAC 2002.Toronto：University of Toronto Press，2002：267-273.

[12]宋彦辉，巨广宏.基于原位试验和规范的岩体抗剪强度与Hoek-Brown准则估值比较[J].岩石力学与工程学报，2012，31（5）：1000-1006. SONG Yan-hui，JUGuang-hong.Determination of rockmass shear strength based on in-situ tests and codes andcomparison with estimation by Hoek-Brown criterion[J].Chinese Journal of Rock Mechanicsand Engineering，2012，31（5）：1000-1006.

[13]郑颖人，赵尚毅.有限元强度折减法在土坡与岩坡中的应用[J].岩石力学与工程学报，2004，23（19）：3381－3388. ZHENG Ying-ren，ZHAO Shang-yi.Application of strength reduction FEM in soil and rock slope[J].Chinese Journal of Rock Mechanics and Engineering，2004，23（19）：3381－3388.

[14]李世辉.隧道围岩稳定系统分析[M].北京：中国铁道出版社，1991. LIShi-hui.Analysisofsurrounding rock stability system on tunnel [M].Beijing：ChinaRailway PublishingHouse，1991.

[15]章光，朱玮申.参数敏感性分析与试验方案优化[J].岩土力学，1993，14（1）：51-57. ZHANGGuang，ZHUYi-wei.Sensitivity analysisof parameter and optimization of experiment scheme[J].Rock and Soil Mechanics，1993，14（1）：51-57.

[16]陈鹏，徐博候.基于因素敏感性的边坡稳定可靠度分析[J].中国公路学报，2012，25（4）：42-48. CHEN Peng，XU Bo-hou.Reliability analysis of slope stability based on factor sensitivity[J].China Journal of Highway and Transport，2012，25（4）：42-48.

[17]牛岩，鲍小成，熊宗海，等.基于灰色关联分析法的边坡敏感性分析[J].地质科技情报，2014，33（3）：202-204. NIU Yan，BAO Xiao-cheng，XIONG Zong-hai，et al.Sensitivity analysis of slope based on the grey relation analysis[J].Geological Scienceand Technology Information，2014，33（3）：202-204.

Sensitivity Analysis of Rock Shear Strength Parameters to the Slope Safety Factor

ZHANGDong-xu1,HOUKe-peng1,YANGZhi-quan1,DU Jun2

(1.Facultyof Land Resource Engineering,Kunming UniversityofScienceand Technology,Kunming 650093,Yunnan,China；2.DepartmentofUrban-Rural Construction and EngineeringManagement,Kunming University,Kunming 650412,Yunnan,China)

The angle of internal friction and cohesion aremain elementswhich affect the stability of slope project and underground project.This paper uses the sensitivity analysis theory to analyze the angle of internal friction and cohesion of its influence on the safety factor of certain open pitmine slope.The rockmassmechanicalparametersare analyzed by applying Hoek-Brown failure criterion and rockmassdirectshear test.The research result indicates that rockmassmechanical parameters applying Hoek-Brown failure criterion are credible;the sensitivity of two factors are similar when the two factors are small.Considering the parameters at 2%rate for the critical point,internal friction Angle of rock slope stability ismore significantwhen the two factorsare comparatively large.

slop;rockmassmechanicalparameters;rockmassdirectshear test;factorofsafety;sensitivity

10.3969/j.issn.1009－0622.2015.04.005

TD164

A

2015-05-16

云南省省级人培项目（KKSY201421016）；云南省教育厅科学研究基金重点项目（2014Z031）

张东旭（1989-），男，河南平顶山人，硕士，主要从事边坡工程研究工作。

侯克鹏（1966-），男，河南南阳人，教授，博士生导师，主要从事岩土工程、采矿工程研究工作。