冻融后预应力混凝土正截面受弯承载力研究

陈月萍，胡强圣，张建飞，张益多

（1.安庆职业技术学院 建筑工程系，安徽 安庆 246003；2.江苏科技大学 土木工程与建筑学院，江苏 镇江 212003）

从地域和气候条件来看，中国的东北地区属于严寒地带，大量的建筑物长期处于冻融环境作用下，遭受冻融破坏，已经造成了重大的经济损失.对长期处于严寒环境作用下的混凝土结构，影响其耐久性的一个非常重要的因素是冻融破坏［1］，因此，有关冻融后混凝土的受弯承载力计算已引起众多学者的关注.当前国内外的规程及规范中所采用的正截面受弯承载力计算公式几乎都是关于普通混凝土和预应力混凝土的，但都没有考虑冻融环境的影响.由前人的大量研究［2－6］可以知道，遭受冻融循环后的混凝土力学性能会发生显著改变，如弹性模量、应力－应变曲线、抗拉强度以及轴心抗压强度等，但对于规范中所给出的正截面受弯承载力计算公式是否还适用于遭受冻融循环影响后的混凝土受弯试件，目前则鲜有研究.基于此，本文借鉴前人在冻融作用后混凝土峰值压应力的变化规律、冻融后混凝土抗拉强度的变化规律、冻融作用后混凝土本构模型等方面已取得的研究成果，参考GB 50010—2010《混凝土结构设计规范》，在试验基础上研究经历冻融后的预应力混凝土梁受弯承载性能，建立反映冻融环境影响的预应力混凝土梁正截面受弯承载力的计算公式，并与试验结果进行对比验证.

1 试验概况

本次试验共设计5根预应力混凝土梁，对应试件编号分别为L1，L2，L3，L4，L5；先将这5根试件分别冻融0，50，100，150，200次，再进行受弯性能试验，以考察冻融作用对试件受力性能的影响.

1.1 试件设计与制作

梁试件L1～L5截面尺寸100mm×100mm，长度515mm，配筋率为1.35%，如图1 所示.混凝土强度等级C40，配合比为m（水泥）∶m（石子）∶m（砂）∶m（水）＝374∶1 164∶723∶184；其中水泥为普通硅酸盐水泥；粗骨料为玄武岩碎石，最大粒径20mm，细骨料为天然江砂，细度模数2.3～2.4；减水剂为JM 系列高效FDN 减水剂，掺量为0.2%（质量分数）；水为日常饮用水.预应力筋采用单根φp5消除应力钢丝，直线型配筋，距梁下表面42mm，其中受拉区预应力筋至受拉边缘的距离ap＝27mm，受拉区纵向普通钢筋至受拉边缘的距离as＝15mm.

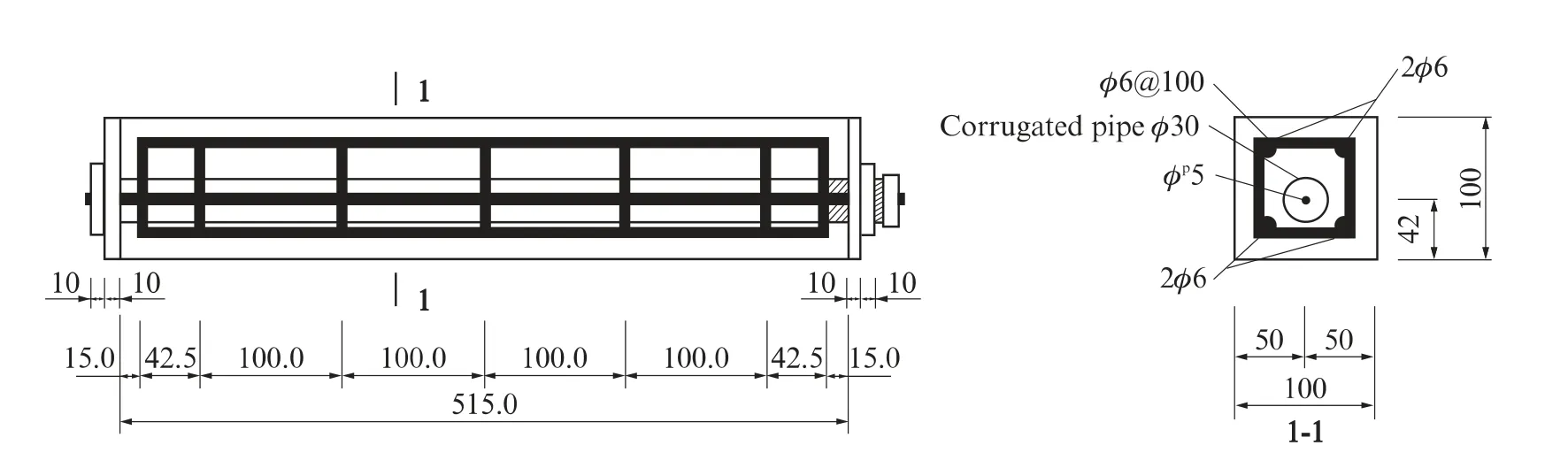
图1 预应力混凝土梁配筋图Fig.1 Reinforcement arrangement of beam specimen（size：mm）

在浇筑每根梁试件的同时，均预留3个混凝土立方体试块（150mm×150mm×150mm）和3个棱柱体试块（150mm×150mm×300mm），用于测定未经冻融的混凝土立方体抗压强度fcu、抗拉强度ft、轴心抗压强度fc及弹性模量Ec；混凝土试块与梁试件均在同条件下养护.混凝土试块的实测力学性能指标见表1，表中数值均为3个试块的平均值.

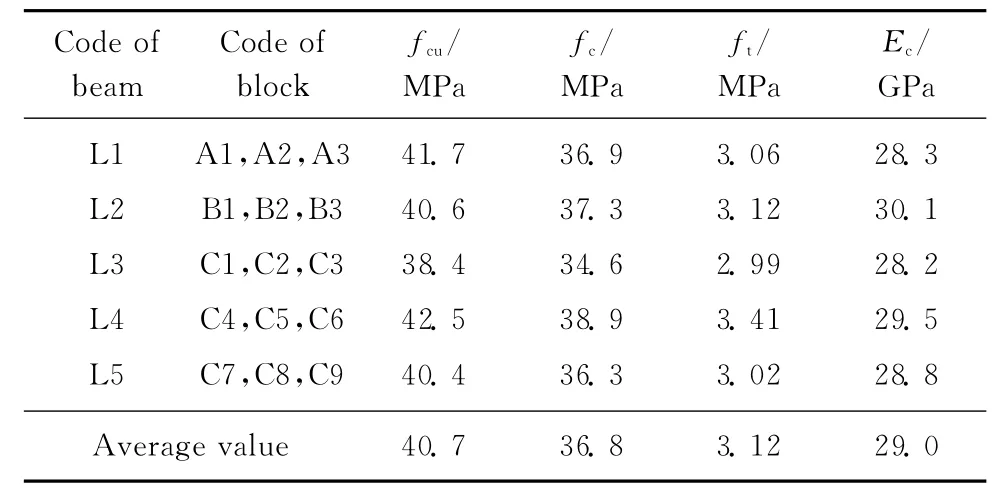
表1 混凝土试块实测力学性能指标Table 1 Actual measured mechanical property index of concrete block

1.2 试验方案

冻融试验按照GBJ 82—85《普通混凝土长期性能和耐久性能试验方法》中的快冻法，在DTR1型快速冻融试验机上进行，每冻融25次停机，采用动弹仪测量试件的动弹性模量并观察试件外观形态的变化.

受弯性能试验在MTS809 拉扭组合材料测试系统上完成，采用三分点加载，如图2所示.荷载上升段采用力控制加载，当加载超过0.8倍计算极限荷载后采用位移控制加载.受弯性能试验在各试验梁的跨中和支座截面均布置了位移计.整个受弯性能试验过程中荷载、应变和位移等均由动态采集设备自动采集.

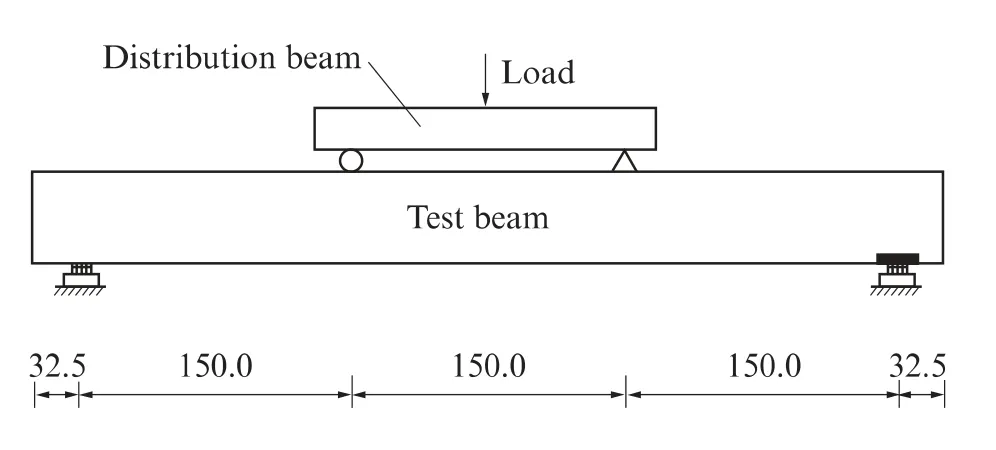
图2 加载示意图Fig.2 Loading scheme（size：mm）

2 冻融后预应力混凝土试件正截面受弯承载力计算公式

2.1 基本假设

本文参考GB 50010—2010来确定遭受冻融作用的预应力混凝土梁正截面受弯承载力计算公式.为考虑冻融作用对试件的影响，本文对冻融作用下受弯试件承载性能的分析作如下基本假定：

（1）为简化计算，不考虑冻融作用导致的混凝土与钢筋之间黏结性能变化对试件受力性能的影响.

（2）计算时不考虑冻融循环引起的试件预应力损失.

（3）冻融作用后受压区混凝土峰值压应变εcd的取值由式（1a）确定，冻融作用后混凝土峰值应力fcd的取值由式（1b）确定［7］：

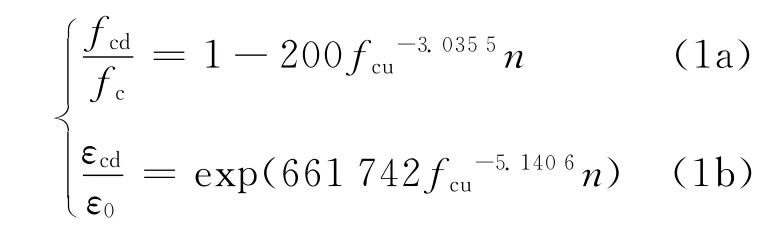
（4）试件受压的应力－应变关系曲线由式（2a），（2b）确定［8］；为简化下降段的计算，参考GB 50010—2010，取斜直线代替应力－应变曲线下降段，斜直线的起点应力为峰值应力fcd，应变为峰值应变εcd；终点为极限应变εcud所对应的点.

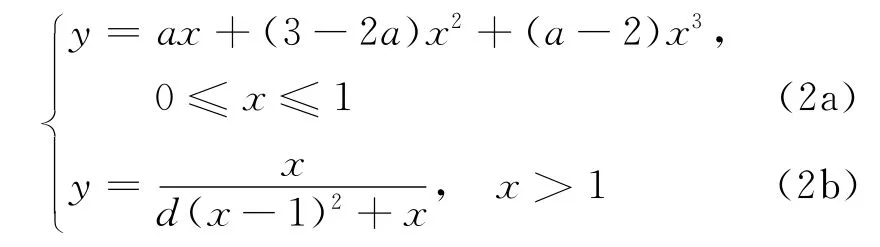
式中：α＝－0.014 3Δpn＋1.744；d＝0.079 6Δpn＋其中的Δpn为经历n 次冻融循环后试件的相对动弹性模量损失率；ε 为试件压应变；σ 为试件压应力；α，d分别为试件的应力－应变曲线上升段和下降段的控制参数；n为冻融循环次数.

2.2 等效矩形应力图的确定

为确定试件的正截面受弯承载力计算公式，由GB 50010—2010的基本假定，需要先确定其等效矩形应力图（当两图形的重心重合且面积相等时，总压力的大小和作用点的位置相同，两图形将等效），如图3所示.设等效图形的受压区高度为βnxn，压应力大小为αnfcd.

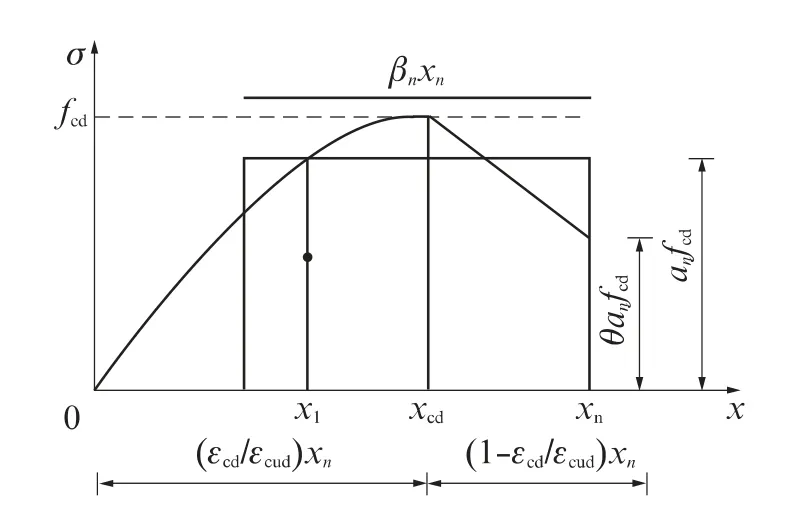
图3 等效矩形应力图Fig.3 Rectangular figure of equivalent compression

由于受压区理论应力图形与应力－应变曲线图形的变量不同，前者的变量是任一受压纤维到中和轴的距离x（x＝0～xn），后者的变量为ε（ε＝0～εcud）.根据图4，由平截面假定原则可得：

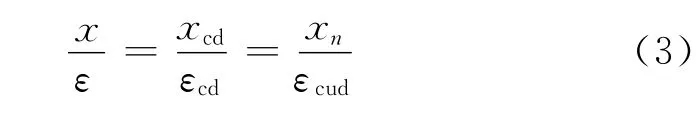
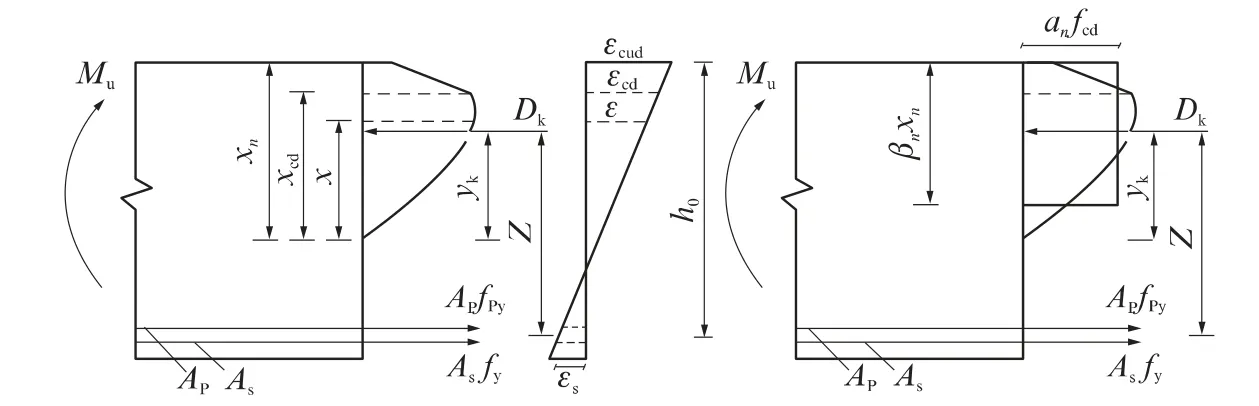
图4 受压区混凝土的应变图和应力图Fig.4 Stress figure and strain figure of compressive region of concrete

图3，4中各符号的含义为：βn 是经历n 次冻融循环后混凝土矩形应力图的受压区高度与中和轴高度xn的比值；αn是经历n 次冻融循环后受压区混凝土矩形应力图的应力值与混凝土峰值应力的比值；θ是经历n 次冻融循环后混凝土极限应变点所对应的应力值与混凝土峰值应力的比值；yk是受压区混凝土压应力合力Dk的形心位置；Mu为弯矩设计值；h0为截面有效高度；As为受压区纵向预应力筋的截面面积；fy为受压区预应力筋的抗压强度；fpy为预应力筋屈服强度；Ap为预应力筋截面面积.

2.3 受压区混凝土的合力

由式（2），（3）可得距离中和轴x 的受压区混凝土各点应力σ（ε）为：当0≤x≤xcd时，0≤ε≤εcd，

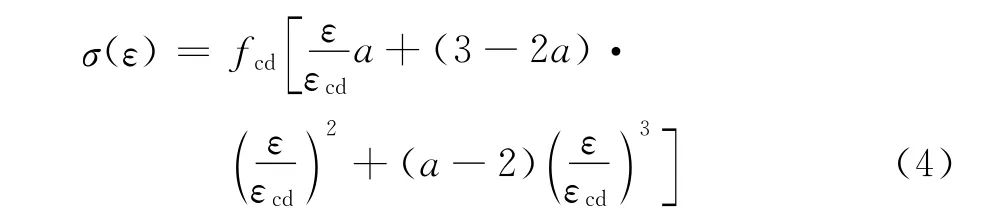
当xcd≤x≤xn时，εcd≤ε≤εcud，根据假设，应力－应变曲线下降段为1条斜直线，直线方程为：

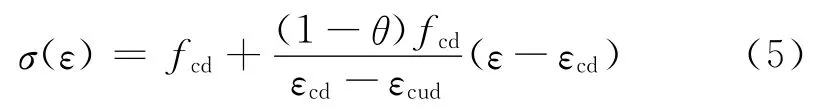
设预应力混凝土受弯试件的截面宽度为b，则受压区试件压应力的合力Dk（即压应力图形的体积∶曲线围成图形的体积和梯形体积之和）为：

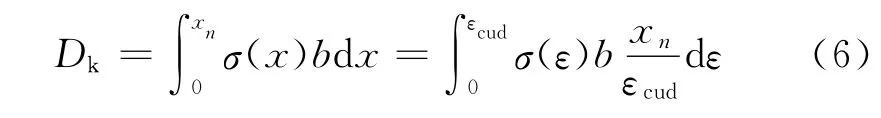
计算得：

由图4，受压区混凝土压应力合力的形心位置yk为：

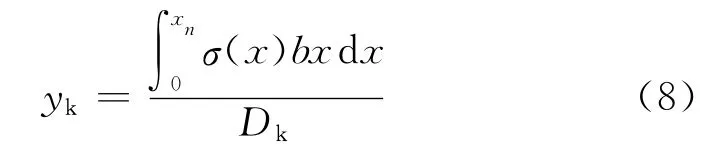
由图3，4并根据应力图形等效原理可得：

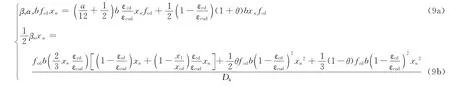
其中曲线段的形心：

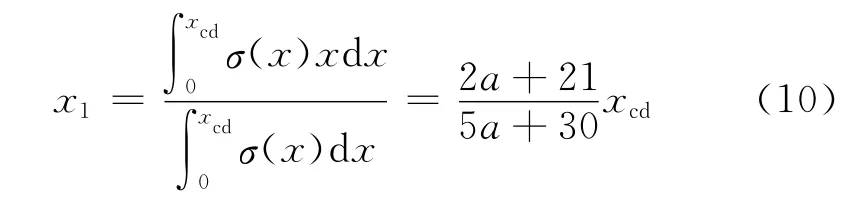
由式（9）可得αn，βn 的公式如下：

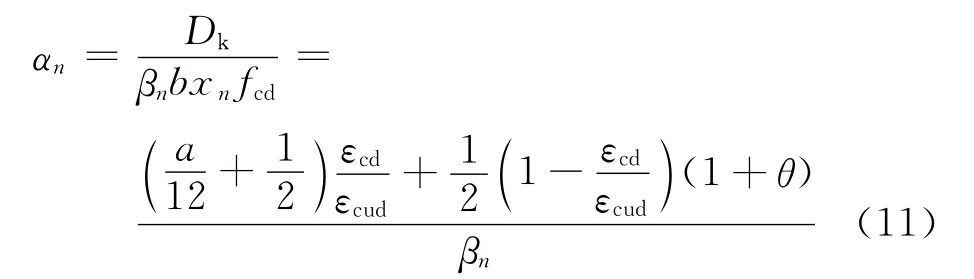
对于经历n次冻融循环后试件的极限应变εcud，本文利用文献［9］的结果，如下式所示：

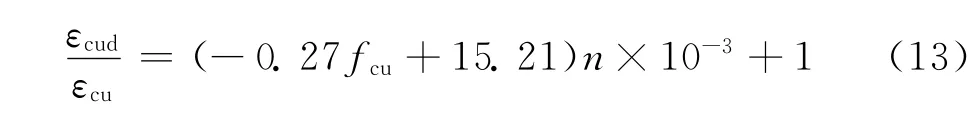
式中：εcu为未经冻融混凝土试块的极限应变.

2.4 αn，βn的回归方程及ξb的计算

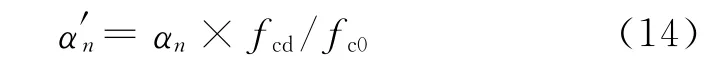
式中：fc0为混凝土轴心抗压强度设计值，由GB 50010—2010中表4.1.4－1确定.

由式（1b），（13）可以分别计算得到经历n 次冻融循环后试件的εcd，εcud值，进而代入式（2b）可以计算得到θ值；试件应力－应变曲线上升段的控制参数α由式（3）计算得到.表2为εcd，εcud，θ，α，x1／xcd的计算结果及经历n 次冻融循环后试件的峰值应力fcd与相对动弹性模量的变化；将表2的计算结果代入式（11），（12），（14），可以计算得到经历n 次冻融循环后试件的等效矩形应力图中2个换算参数，βn之值，结果见表3.

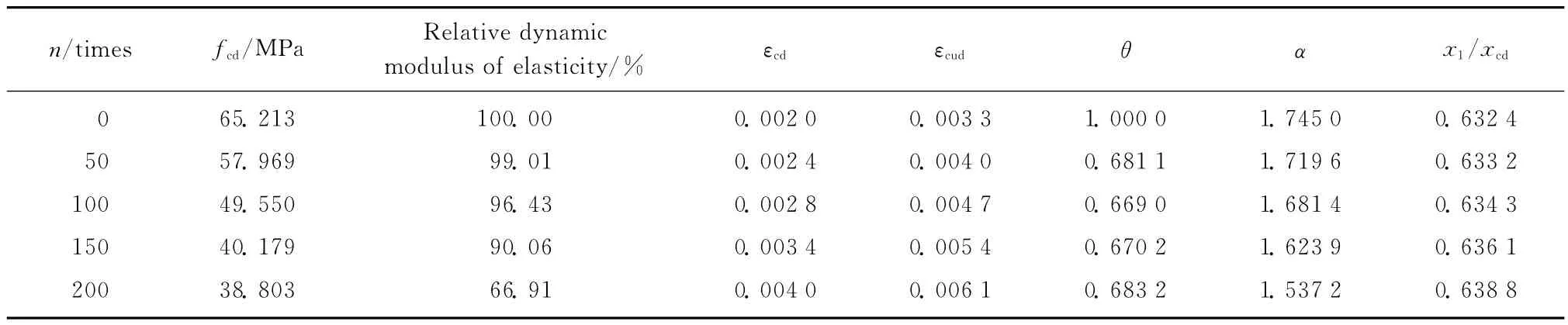
表2 经历n次冻融循环后试件的εcd，εcud，θ，α，x1／xcd值Table 2 Dates ofεcd，εcud，θ，α，x1／xcdafter ntimes of freeze－thaw

表3 经历n次冻融循环后试件的，βn值Table 3 Dates of，βnafter ntimes of freeze－thaw

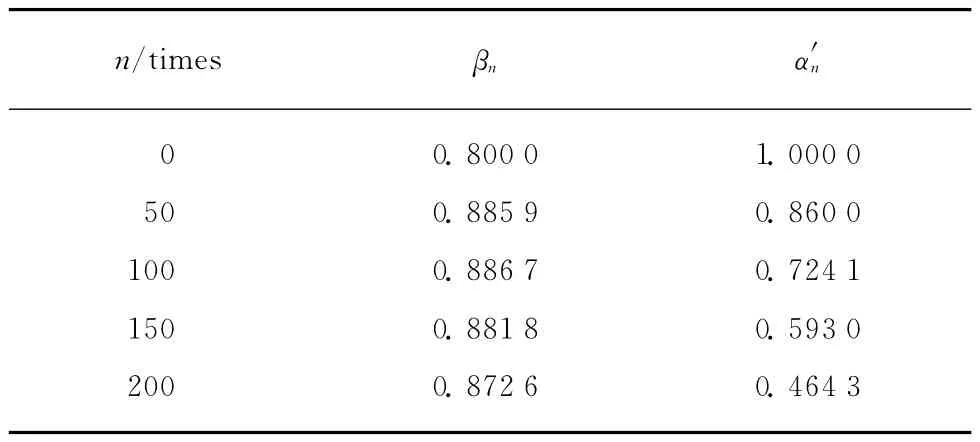
表3 经历n次冻融循环后试件的，βn值Table 3 Dates of，βnafter ntimes of freeze－thaw

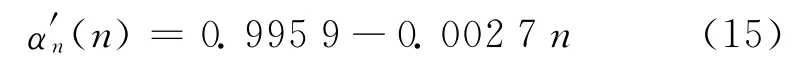
同理，采用Origin 8软件对表3中βn 的数据进行拟合，得到βn 与冻融循环次数n 的回归方程：

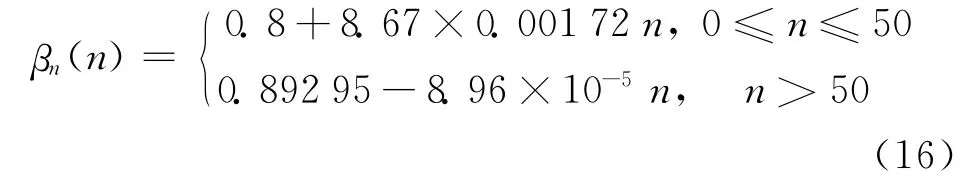
本文所用预应力筋为消除应力钢丝，属于无明显屈服点的预应力钢筋，由GB 50010—2010 中ξb（界限破坏时预应力混凝土试件相对受压区高度）的计算公式（见式（17）），可以得到经历冻融0，50，100，150，200次试件的ξb 值，见表4.

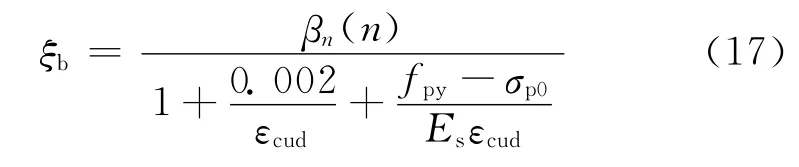
由表4可以看出，随着冻融循环次数的增加，ξb值逐渐增大，这是因为在冻融的破坏作用下，预应力混凝土试件的裂缝会增长，其内部结构会逐渐变得酥松并不断退化，由式（13）可知，此时混凝土的极限应变会不断增加，从而使得ξb 值逐渐增大.同样为准确表达ξb 与冻融循环次数n 的数学关系，通过Origin 8软件对表4数据进行二次多项式拟合，可以得到ξb（n）的回归方程：

表4 经历n次冻融循环后试件的ξb值Table 4 Dates ofξbafter ntimes of freeze－thaw

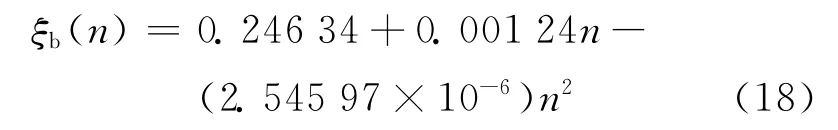
2.5 冻融后预应力混凝土极限承载力计算公式

参考GB 50010—2010中预应力混凝土试件在使用阶段的正截面受弯承载力计算公式，根据前述得到的的计算结果，可以得到冻融作用后预应力混凝土试件使用阶段正截面受弯承载力的计算公式为：

3 理论计算值与试验值的对比

通过式（19），（20）可以计算得到经历n 次冻融循环后的预应力混凝土试件正截面受弯承载力.为验证理论计算值的合理性，将其与试验值进行对比，结果见表5.

由表5可得：经历n 次冻融循环后的预应力混凝土试件在使用阶段的正截面受弯承载力理论计算值略小于试验值，原因是在冻融循环过程中钢筋会对混凝土损伤的发展起到制约作用，而且影响试验过程的因素很多（如人为作用和环境影响），且一般情况下采用GB 50010—2010进行理论计算都是偏保守安全的，在未经冻融时本次试验值与理论计算值的差值为11.1%，误差在20%以内，是符合要求的.所以式（19）能反映冻融作用后预应力混凝土试件在使用阶段的正截面受弯承载力的一般规律.更加精确的计算结果依赖于采用更精确的冻融混凝土本构模型.

4 结论

（1）参考GB 50010—2010，得出了经历n 次冻融循环后预应力混凝土矩形应力图的受压区高度与中和轴高度xn的比值βn、经历n次冻融循环后预应力混凝土矩形应力图的应力值与混凝土轴心抗压强度设计值的比值的计算公式；通过Origin 8软件对试验值进行拟合，得出了与冻融循环次数n的回归方程式.

（3）根据冻融作用后混凝土的应力－应变本构模型，参考GB 50010—2010，得到了冻融作用后预应力混凝土试件在使用阶段的正截面受弯承载力计算公式.

（4）比较了经历n 次冻融循环后预应力混凝土试件在使用阶段的正截面受弯承载力理论计算值与试验值，验证了本文得到的计算公式能反映冻融作用后预应力混凝土试件在使用阶段的正截面受弯承载力的一般规律.

［1］朱江.预应力混凝土梁在冻融循环后的受力性能研究［D］.扬州：扬州大学，2006.ZHU Jiang.Characteristic investigation of the prestressed concrete beams under cyclic freezing and thawing［D］.Yangzhou：Yangzhou University，2006.（in Chinese）

［2］邹超英，赵娟，梁锋，等.冻融作用后混凝土力学性能的衰减规律［J］.建筑结构学报，2008，29（1）：117－123.ZOU Chaoying，ZHAO Juan，LIANG Feng，et al.Degradation of mechanical properties of concrete caused by freeze－thaw action［J］.Journal of Building Structures，2008，29（1）：117－123.（in Chinese）

［3］SUN W，ZHANG Y M，YAN H D.Damage and damage resistance of high strength concrete under the action of load and freezing－thawing cycles［J］.Cement and Concrete Research，1999，29（6）：1519－1523.

［4］BISHNOI S.Strain－temperature hysteresis in concrete under cyclic freeze－thaw conditions［J］.Cement and Concrete Composites，2008，30（5）：374－380.

［5］HASAN M，NAGAI K，SATO Y，et al.Tensile stress－crack width model for plain concrete damaged by freezing and thawing action［C］∥Proc JCI.［S.l.］：［s.n.］，2002：109－114.

［6］施士升.冻融循环对混凝土力学性能的影响［J］.土木工程学报，1997，30（40）：35－42.SHI Shisheng.Effect of freezing－thawing cycles on mechanical properties of concrete［J］.Journal of Civil Engineering，1997，30（40）：35－42.（in Chinese）

［7］段安，钱稼茹.受冻融环境混凝土的应力－应变全曲线试验研究［J］.混凝土，2008（8）：13－16.DUAN An，QIAN Jiaru.Experimental study on complete compressive stress－strain curve of concrete subjected to freeze－thaw cycles［J］.Concrete，2008（8）：13－16.（in Chinese）

［8］邹超英，赵娟，梁锋，等.冻融环境下混凝土应力－应变关系的试验研究［J］.哈尔滨工业大学学报，2007，39（2）：229－231.ZOU Chaoying，ZHAO Juan，LIANG Feng，et al.Experimental study on stress－strain relationship of concrete in freeze－thaw environment［J］.Journal of Harbin Institute of Technology，2007，39（2）：229－231.（in Chinese）

［9］曹大富，富立志，杨忠伟，等.冻融循环作用下混凝土受压本构特征研究［J］.建筑材料学报，2013，16（1）：17－23.CAO Dafu，FU Lizhi，YANG Zhongwei，et al.Study on constitutive relations of compressed concrete subjected to action of freezing－thawing cycles［J］.Journal of Building Materials，2013，16（1）：17－23.（in Chinese）