基于DIC方法的地聚合物混凝土断裂过程分析

谢子令，周华飞，杨克家，孙林柱

（温州大学 建筑工程学院，浙江 温州 325035）

地聚合物材料是近年来新发展起来的一类碱激发胶凝材料［1］.与水泥胶凝材料相比，其具有较低的碳排放量［2－3］，较好的耐久及耐腐蚀性［4－5］、耐高温性［6］以及较高的钢筋黏结力［7］等特点，可作为胶凝材料来制备混凝土材料及其构件［8－9］.然而地聚合物混凝土与普通的水泥混凝土类似，是准脆性材料，易发生脆性断裂，因此研究及掌握其断裂行为是将该材料应用于结构工程的关键问题之一.近年来，国内外研究者对纤维增强地聚合物以及素地聚合物混凝土的断裂韧性进行了一些研究［10－13］，得出了地聚合物混凝土断裂韧性较同强度等级水泥混凝土断裂韧性高的一致性结论，但在地聚合物混凝土断裂过程方面的研究鲜见报道，同时在水泥混凝土断裂力学方面的研究成果能否直接用于地聚合物混凝土还有待深入研究.

数字图像相关（DIC）方法是根据物体表面随机分布的粒子光强在变形前后的概率统计相关性来确定物体的位移或变形的光学测量方法，具有全场性、非接触式和三维等独特优点［14］.该方法已被成功应用于材料断裂过程的裂纹扩展行为［15－17］以及构件破坏［18］等方面的研究.

本文结合DIC方法与传统夹持引伸计方法，对含预制缺口的粉煤灰基地聚合物混凝土试样在三点弯曲加载过程中的裂缝张开位移以及裂缝扩展长度进行了定量化的研究.首先基于DIC测试的位移场u，得到预制裂缝口张开位移（crack－mouth－opening displacement，CMOD），将其与基于夹持引伸计测试结果进行对比来验证DIC测试结果的准确性；随后将DIC测试的裂尖张开位移（crack－tip－opening displacements，CTOD）与基于弹性等效裂缝的计算结果进行对比分析，旨在揭示粉煤灰基地聚合物混凝土断裂过程的裂缝演化，以及探讨用于描述水泥混凝土断裂过程的弹性等效裂缝方法在地聚合物混凝土材料上应用的可行性；最后对比分析裂缝扩展长度Δa的DIC测试值与基于弹性等效裂缝方法下的计算值，以揭示实际的微裂纹区与计算等效裂缝的区别.

1 试验

1.1 原材料

制备地聚合物混凝土所用的胶凝材料为低钙粉煤灰及少量S95级粒化高炉矿渣；砂为中砂（细度模数2.4）；粗骨料为粒径小于20mm 的碎石；激发剂采用18mol／L的氢氧化钠溶液与市售泡花碱（相对密度1.35，模数3.3，其中Na2O，SiO2，H2O 的质量分数分别为7.9%，27.9%，64.2%）按1∶3（质量比）混合而成.

1.2 地聚合物混凝土试样的制备

根据前期大量配合比设计，选定制备地聚合物混凝土所用石子、砂、粉煤灰、矿渣和复合激发剂用量分别为1 050，565，420，180，200kg／m3.在该配比下制备的粉煤灰基地聚合物混凝土的强度高，且流动性好.称取规定量的砂、粗骨料以及粉煤灰倒入双卧轴混凝土搅拌机中，干拌5min，加入规定量的激发剂溶液再搅拌5min，将拌和物装入100mm×100mm×515mm 试模中，振动成型5min，并在成型面覆盖聚乙烯膜.将成型试件放入60℃烘箱中养护24h后脱模，然后放置在室内环境至28d龄期，最后采用岩石切割机进行预制缺口的切割，预制缺口宽度为3mm，长度a0为20mm.

1.3 试验装置

通过电子万能试验机对预制缺口粉煤灰基地聚合物混凝土试样进行三点弯曲加载，加载速率为0.05mm／min.通过夹持引伸计测试预制缺口处的张开位移CMOD，固定引伸计的楔形垫块厚度H0为1.7mm，试样跨度S，宽度t 和高度b 分别为400，100和100mm，加载示意见图1.通过2台工业相机对试样预制缺口附近的散斑图像进行同步采集，采集频率为10Hz，将采集的照片导入数字图像相关分析软件（Vic 3D，CSI）进行分析，即可得到裂缝附近变形场及其演化过程.

1.4 基于DIC方法的CTOD 及Δa的确定

预制切口尖端张开位移CTOD 及裂缝扩展长度Δa是断裂力学分析中2个重要参数，图2给出了这2个参数的定义.

图1 单边缺口三点弯曲试样Fig.1 Single－edge－cracked three－point bend specimen（size：mm）

图2中，裂缝的萌生及扩展将导致裂缝左右两侧位移u 的突变，而其突变量即为裂尖张开位移CTOD，基于DIC技术可测试出不同荷载作用下试样的表面位移场.图3显示了不同荷载作用下，u 沿过裂缝尖端直线MN（y＝0）上的分布情况.

图2 裂缝尖端示意图Fig.2 Schematic near crack tip

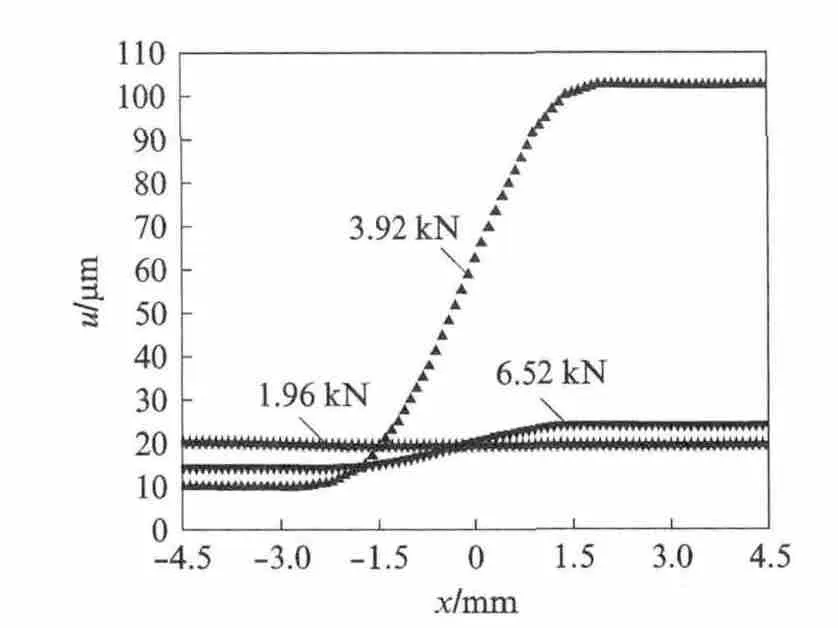
图3 不同荷载下试样MN 线上位移u 的分布Fig.3 Displacements ualong line MN on specimen at three load points

由图3可见，在加载初期，荷载增大至1.96kN（0.3Pmax，Pmax为峰值荷载），u 值随着x值线性变化，无明显突变，这表明裂缝口未出现开裂；当荷载增大至6.52kN（Pmax）时，u值在裂缝口附近出现突变，两侧的突变量为9.7μm，表明裂缝已经扩展，CTOD为9.7μm；当荷载降低至3.92kN（0.6 Pmax）时，u值急剧增大，CTOD 达到92.7μm.因此通过跟踪分析裂纹尖端u 值的突变量，即可得到不同荷载作用下CTOD 的演化过程.

通过分析不同荷载作用下，裂缝尖端附近u场沿y轴方向分布情况，可了解裂纹的扩展行为.图4（a）显示了峰值荷载作用下，沿裂缝扩展方向区域的u场分布情况.由图4（a）可以看出，在裂缝口附近u场出现明显突变，表明试样已开裂.进一步对裂缝尖端区域的u场沿x 方向进行求导，并绘制出du／dx 沿y轴（裂缝扩展方向）的变化趋势图，如图4（b）所示，由此可确定该荷载下裂缝扩展长度Δa为11.5mm.因此基于DIC测试的位移场可得到不同荷载作用下的CTOD及Δa等重要断裂力学指标.

1.5 基于夹持引伸计方法的CTOD 及Δa的确定

图4 峰值荷载作用下裂缝附近的u场分布情况Fig.4 Displacement uat the load of Pmax

预制缺口试样在三点弯曲过程中裂缝口张开位移CMOD，荷载P 及裂缝长度a（初始裂缝长度a0与裂缝扩展长度Δa 之和）之间的关系可由式（1）表示［19］：

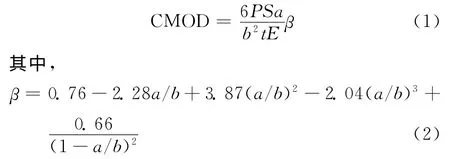
式中：E 为试样的弹性模量.

考虑到固定夹持引伸计楔形块厚度H0的影响，对式（1）进行修正［20］，结果见式（3）：

在本文的计算中，E 的确定是将P－CMOD 曲线中线性段（0.2Pmax～0.4Pmax）的斜率值（P／CMOD）代入式（3）并取a＝a0计算得到的，该试样的弹性模量为30.7GPa.

基于夹持引伸计法的P－CMOD测试结果，通过迭代法对式（2），（3）进行求解，可计算出不同P 值下的裂缝长度a，进而根据Δa＝a－a0，得到裂缝扩展长度Δa的演化情况.

裂缝口张开位移CMOD 与任意点裂缝张开位移（crack－opening－displacements，COD）的关系可由式（4）给出［21］：

式中：x 为任意点到距裂缝口的距离.

将CMOD 的测试结果及裂缝长度a 的计算结果代入式（4），并取x＝a0＋H0（楔形块厚度修正）可计算出裂尖张开位移CTOD.

2 试验结果与分析

首先基于DIC 测试预制裂缝口两侧的位移场u，并根据1.4小节阐述的方法，可得到预制裂缝口张开位移CMOD，将其与基于夹持引伸计测试结果进行对比，来验证DIC 测试结果的准确性；随后将DIC测试的CTOD 与基于式（2），（3）和（4）的计算结果进行对比分析，来探讨计算公式对于地聚合物混凝土的适用性；最后对比分析Δa 的测试值与计算值，以揭示实际的微裂纹区与计算等效裂缝的区别.

2.1 DIC测试结果准确性验证

基于DIC测试的CMOD 是预制裂缝口处的张开位移，而夹持引伸计测试的是预制裂缝口外1.7mm（H0＝1.7mm）处的张开位移，两者的比值近似等于（Δa＋a0）／（Δa＋a0＋H0），对于a0＝20mm的试样，其最大偏差为6.8%，且随着裂缝扩展长度Δa的增大而减小，因此本文未考虑此差别带来的影响，直接将两者进行对比分析，其结果如图5所示.由图5可以看出，两种方法测试结果吻合较好，表明基于DIC方法的位移场测试精度与传统夹持引伸计法相当.在荷载的上升段，即低CMOD 值下，DIC测试结果波动较大，但与夹持引伸计测试结果基本吻合；峰值荷载后，随着CMOD 增大，DIC 测试结果比较稳定，且与夹持引伸计测试结果吻合较好.P－CMOD曲线经历线性o－a 段、非线性a－b 段、P随CMOD 增大而缓慢下降的b－c 段以及P 急剧减小的c－d 段.

图5 P－CMOD曲线图Fig.5 Curves of P－CMOD

2.2 CTOD 及Δa的测试与计算结果对比分析

图6给出的是P－CTOD 曲线图.由图6 可见，在加载初期CTOD 随P 线性增加，这表明试样处于弹性变形阶段，预制缺口尖端区域无新裂缝产生；当P 增大至4.4kN（0.646Pmax）附近时，P－CTOD 变化趋势逐渐偏离初始的线性段，表明裂缝尖端出现了新的损伤，对应着试件的起裂［20］.与图5 的结果类似，根据曲线斜率变化可将P－CTOD 曲线分成4个阶段，即初始的线性o－a 段；a－b段的裂缝稳态扩展阶段，此阶段CTOD 随P 增大而增大；b－c 段的裂缝亚稳态扩展阶段，此阶段P 随CTOD 增大而缓慢减小，CTOD 从9.8μm 增大至28.0μm，而荷载从Pmax降低至0.964Pmax，降低了3.6%；c－d 段的失稳破坏阶段，此阶段P 随CTOD 的增大而迅速减小.对比DIC测试结果与基于式（2），（4）的计算结果可以看出两者在试样开裂后存在一定的偏差，特别是在裂纹失稳扩展的c－d 段，但最高偏差也仅6%左右，随后两者的结果趋于一致.可见用于描述水泥混凝土的裂缝扩展的式（2），（4）能较好地描述地聚合物混凝土P－CTOD演化关系.

图6 P－CTOD曲线图Fig.6 Curves of P－CTOD

图7显示了P－Δa 测试及计算结果.显然依据曲线斜率的变化可将P－Δa 曲线分成4 个阶段，即Δa为零的线性o－a 段；Δa随P 的增大而增大的a－b段；过峰值荷载（b点）后出现了P－Δa 曲线小斜率平台的b－c 段，即裂缝的亚稳态扩展阶段；随后随着Δa的增大，试件的抗力P 迅速减小，即进入裂纹失稳扩展的c－d 段.

图7 P－Δa关系曲线Fig.7 Load vs.crack extension length

对比图6，7可以看出，P－CTOD与P－Δa曲线具有较高的相似性，这表明CTOD与Δa具有一定的相关 性.当P增大至3.9～4.4 kN（0.600Pmax～0.646Pmax）时，Δa保持为零，表明预制裂缝未发生扩展.当荷载增大至4.56kN（0.7Pmax）时，Δa 增大至3.92mm，表明该荷载作用下，预制缺口处新的裂缝已萌生并向前扩展.然而，基于式（2），（3）计算得到的裂缝扩展长度Δa与基于DIC 测试的微裂纹扩展长度Δa偏差较大，偏离程度随荷载呈现先增后降的趋势，如峰值后P 降低至5.3kN 附近时，Δa 的DIC测试值为50.34mm，而基于式（2），（3）的计算值仅为31.62mm，较DIC测试结果小了37.2%，如图7所示.鉴于CTOD 测试及计算值吻合较好，而CTOD 与裂缝扩展存在一定的关联，将测试及计算的CTOD 与Δa的关系曲线进行对比分析，其结果如图8所示.由图8可见，相同的CTOD 下，Δa 实测值较基于式（2），（3）的计算值大，其差值随荷载裂纹演化过程呈先增后降的趋势.

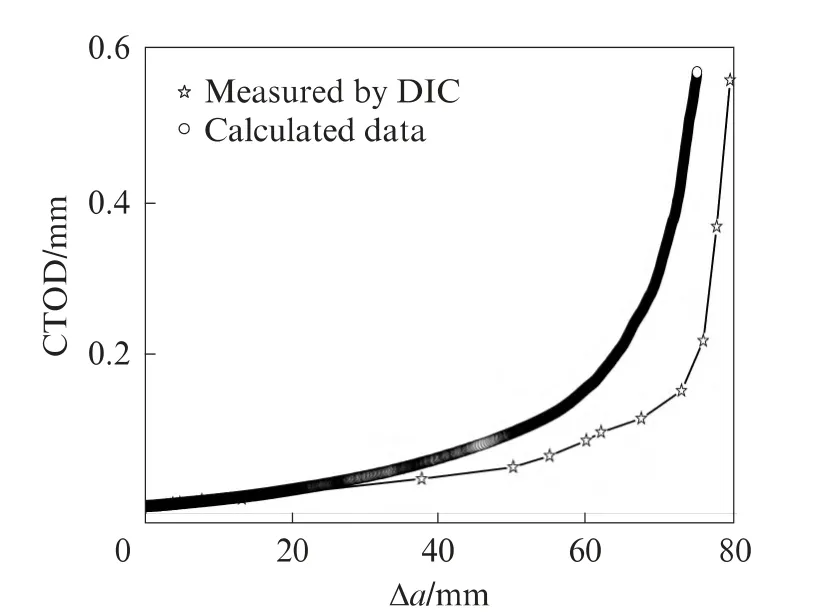
图8 CTOD－Δa关系曲线Fig.8 CTOD vs.crack extension length

导致裂缝扩展长度测试值与计算值差别较大的主要原因是由于地聚合物混凝土与混凝土类似，均属于准脆性材料.在其断裂过程中，裂缝尖端会形成一个微裂缝区，即断裂过程区，见图9中DIC 测试的Δa涵盖区.该区域内裂缝并非完全是表面无应力的自由裂缝，而是包含了部分仍能传递黏聚应力的微损伤带［21］.描述荷载P，裂缝口张开位移CMOD 及裂缝长度a之间的关系式（1），（2）是以自由裂缝两侧的张开位移测试值为定解条件，对双调和应力函数级数解的待定常数进行确定，进而建立描述P－CMOD－a 关 系 的 方 程［22］.由于预制缺口根部及缺口尖端处均属于自由裂缝上的点，其两侧的张开位移CMOD 及CTOD 的测试值自然满足式（1），（2）的关系，详细结果如图5，6所示.因此，基于DIC测试的CMOD 及P 值，并通过式（1），（2）计算得到的裂缝长度a 是指表面无应力的自由裂缝长度，即在保证P－CMOD 相等的前提下，将裂缝面上分布着黏聚力的微裂纹等效为裂缝面上黏聚力为零的应力自由裂缝.等效裂缝扩展长度如图9中虚线部分所示，显然在P－CMOD 相等的条件下，无黏聚力作用的等效裂缝扩展长度Δa 较实际有黏聚力存在的裂缝扩展长度Δa 小.因此根据宏观的PCMOD测试结果，运用有限元方法反演得到的材料断裂过程区裂缝张开位移与黏聚力之间的本构关系并非材料的本征特性，应基于裂纹扩展区位移的场变量进行反演断裂过程区的本征本构［23］.

图9 裂缝扩展长度模型Fig.9 Model for crack extension length

3 结论

（1）基于DIC方法测试的裂缝张开位移与夹持引伸计测试值吻合较好，该方法能较好地测试出试样断裂过程的裂缝演化行为.

（2）地聚合物混凝土断裂过程经历了起裂、裂缝的稳态、亚稳态扩展及失稳破坏阶段.

（3）用于水泥混凝土断裂过程描述的弹性等效裂缝方法，能较好地反映地聚合物混凝土宏观自由裂缝张开行为.

（4）基于DIC的裂缝扩展长度的测试值与弹性等效裂缝扩展长度的计算值之间存在较大的偏差，导致这一差别的主要原因是由于地聚合物混凝土与水泥混凝土一样，均存在断裂过程区.

［1］van DEVENTER J S J，PROVIS J L，DUXSON P.Technical and commercial progress in the adoption of geopolymer cement［J］.Minerals Engineering，2012，29：89－104.

［2］van DEVENTER J S J，PROVIS J L，DUXSON P，et al.Chemical research and climate change as drivers in the commercial adoption of alkali activated materials［J］.Waste and Biomass Valorization，2010，1（1）：145－155.

［3］TURNER L K，COLLINS F G.Carbon dioxide equivalent（CO2－e）emissions：A comparison between geopolymer and OPC cement concrete［J］.Construction and Building Materials，2013，43：125－130.

［4］BAKHAREV T.Durability of geopolymer materials in sodium and magnesium sulfate solutions［J］.Cement and Concrete Research，2005，35（6）：1233－1246.

［5］BAKHAREV T.Resistance of geopolymer materials to acid attack［J］.Cement and Concrete Research，2005，35（4）：658－670.

［6］BAKHAREV T.Thermal behaiviour of geopolymers prepared using calss F fly ash and elevated temperature curing［J］.Cement and Concrete Research，2006，36（6）：1134－1147.

［7］SARKER P M.Bond strength of reinforcing steel embedded in fly ash－based geopolymer concrete［J］.Materials and Structures，2011，44（5）：1021－1030.

［8］SUMAJOUW D M J，HARDJITO D，WALLAH S E，et al.Fly ash－based geopolymer concrete：study of slender reinforced columns［J］.Journal of Materials Science，2007，42（9）：3124－3130.

［9］YOST J R，RADLINSKA A，ERNST S，SALERA M.Structural behavior of alkali activated fly ash concrete.Part 2：Structural testing and experimental findings［J］.Materials and Structures，2013，46（3）：449－462.

［10］DIAS D P，THAUMATURGO C.Fracture toughness of geopolymeric concretes reinforced with basalt fibers［J］.Cement ＆Concrete Composites，2005，27（1）：49－54.

［11］DEEPA R S，ABRAHAM R，GANESAN N，et al.Fracture properties of fiber reinforced geopolymer concrete［J］.International Journal of Scientific ＆Engineering Research，2013，4（5）：75－80.

［12］SARKER P K，HAQUE R，RAMGOLAM K V.Fracture behaviour of heat cured fly ash based geopolymer concrete［J］.Materials and Design，2013，44（2）：580－586.

［13］LIN Tiesong，JIA Dechang，HE Peigang，et al.Effects of fiber length on mechanical properties and fracture behavior of short carbon reinforced geopolymer matrix composites［J］.Materials Science and Engineering A，2008，497（1－2）：181－185.

［14］SUTTON M A，ORTEU J J，SCHREIER H.Image correlation for shape，motion and deformation measurements：Basic concepts，theory and applications［M］.New York：Springer，2009：81－116.

［15］YATES J R，ZANGANEH M，TAI Y H.Quantifying crack tip displacement fields with DIC［J］.Engineering Fracture Mechanics，2010，77（11）：2063－2076.

［16］NUNES L C S，REIS J M L.Estimation of crack－tip－opening displacement and crack extension of glass fiber reinforced polymer mortars using digital image correlation method［J］.Materials and Design，2012，33（1）：248－253.

［17］WU Zhimin，RONG Hua，ZHENG Jianjun，et al.An experimental investigation on the FPZ properties in concrete using digital image correlation technique［J］.Engineering Fracture Mechanics，2011，78（17）：2978－2990.

［18］AGGELIS D G，VERBRUGGEN S，TSANGOURI E，et al.Characterization of mechanical performance of concrete beams with external reinforcement by acoustic emission and digital image correlation［J］.Construction and Building Materials，2013，47：1037－1045.

［19］TADA H，PARIS P C，IRWIN G R.The stress analysis of cracks handbook［M］.3rd ed.New York：ASME Press，2000：58－59.

［20］XU Shilang，REINHARDT H W.Determination of double－K criterion for crack propagation in quasi－brittle fracture.PartⅡ：Analytical evaluation and practical measuring methods for three－point bending notched beams［J］.International Journal of Fracture，1999，98（2）：151－177.

［21］JENQ Y S，SHAH S P.Two parameter fracture model for concrete［J］.Journal of Engineering Mechanics，1985，111（10）：1227－1241.

［22］GROSS B，ROBERTS E J，SRAWLEY J E.Elastic displacements for various edge－cracked plate specimens［J］.International Journal of Fracture Mechanics，1968，4（3）：267－276.

［23］SHEN Bin，STANCIULESCU I，PAULINO G H.Inverse computation of cohesive fracture properties from displacement fields［J］.Inverse Problems in Science and Engineering，2010，18（8）：1103－1128.