基于孔结构参数的混凝土气体扩散模型

汤玉娟，左晓宝，殷光吉

（南京理工大学 理学院，江苏 南京 210094）

在大气环境下，混凝土碳化所引起的钢筋锈蚀是导致混凝土结构耐久性退化的重要因素之一［1］.大气中的二氧化碳、氧气和水蒸气等气体在混凝土中的扩散系数是影响混凝土碳化速率和钢筋锈蚀速率、分析混凝土结构耐久性退化规律的重要参数［2－3］.因此，建立气体在混凝土中的扩散模型是分析混凝土结构耐久性退化规律的基础［3］.

目前，学者们通过各种手段研究了二氧化碳、氧气等气体在混凝土中的扩散性能，建立了相应的气体扩散模型［2－8］.Papadakis等［5］通过试验研究了二氧化碳和氧气在混凝土中的扩散性能，给出了二氧化碳扩散系数的经验公式；Bother等［7］建立了不同水饱和度下的气体扩散模型，分析了材料初始饱和度对气体扩散的影响；牛荻涛等［2］提出了以混凝土抗压强度为主要参数，同时考虑环境温度、相对湿度、混凝土的应力状态与应力水平等综合影响的气体有效扩散系数计算模型；耿欧等［8］根据Fick第二定律和氮吸附法研制出了氧气扩散系数测试装置，测试并分析了水灰比、环境温度和相对湿度对混凝土中氧气扩散系数的影响规律，给出了氧气扩散系数的预测模型.上述模型仅能反映混凝土宏观组成及性能参数（水灰比、强度等）对气体扩散性能的影响，而气体在混凝土中的扩散还受到孔隙率、曲折度等微观结构参数的影响［9］.建立反映混凝土复杂孔结构特征的简化模型，是研究气体在混凝土中扩散规律的基础.但通过宏观试验方法所建立的气体扩散模型难以定量描述混凝土微观结构对气体扩散性能的影响.分形理论是近年来发展起来的一门新兴学科，通过孔结构参数的分形表征，能定量描述混凝土微观结构参数对气体扩散性能的影响规律［10－11］.

本文根据混凝土微观结构特征，建立了混凝土孔结构的简化模型，并运用分形维数来表征孔数目、孔隙率、曲折度等参数，在此基础上，结合气体在单根（干燥、湿润）毛细管中的扩散特点，建立了考虑水饱和度影响的混凝土气体扩散模型，以进一步开展大气环境下混凝土结构碳化引起的耐久性退化规律研究.

1 混凝土孔结构简化模型

混凝土是由骨料和水泥水化产物组成的固体骨架以及不同尺度的孔隙构成的多孔复合材料，其孔结构具有随机性、不规则性和复杂性，是影响混凝土中气体扩散性能的关键因素［2］.为了建立与混凝土实际孔结构相一致的简化模型，根据SEM 和X 射线－CT 等观察结果，作如下基本假设：（1）混凝土孔结构为由数量不等、孔径不一的变截面子毛细管束组成的管束结构，各毛细管轴线相互平行且曲折度相同，环境介质在各毛细管之间的扩散过程相互独立；（2）混凝土实际孔结构与简化模型的孔隙率相等；（3）为考虑水饱和度对气体扩散性能的影响，认为水分子均匀吸附在孔通道的管壁内侧.

根据以上基本假设，可将混凝土孔结构简化为如图1（a）所示的毛细管束模型，该模型包含有k 类子毛细管束，且每类子毛细管束由Ni（i＝1，2，…，k）个毛细管组成，毛细管的剖面图如图1（b）所示，其管径r随孔深x 的变化关系为：

式中：ri（x）为第i类子毛细管束中单根毛细管在孔深x 处的管径，m；rmin，i，rmax，i和rm，i分别为毛细管的最小管径、最大管径和平均管径，m；di为图1（b）中A，B 两点间的距离，m；gi为图1（b）中O，A 两点间距离与di的比值，m；Li为毛细管的长度，Li＝（1＋gi）di，m.

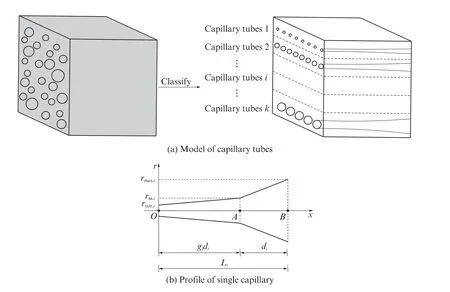
图1 混凝土孔结构简化模型Fig.1 Simplified model of concrete pore structure

混凝土孔结构的测试结果［11］表明，其最大孔径（rmax）与最小孔径（rmin）之比可达104～105，即rmin／rmax→0.分形理论的判据［12－14］为：

式中：Df为孔体积分形维数，可通过压汞法获得［10］.由式（2）可知，混凝土孔结构特征基本满足分形理论的判据，故可视混凝土为分形材料，利用分形理论［12－14］，对毛细管束模型中第i类子毛细管束的孔数目Ni和孔隙率φi等可用分形维数表征：

根据相关文献［11－12］，混凝土孔结构的平均曲折度τ与其孔隙率有关：

式中：ωwc为调整系数；ηr 为形状因子；hα为混凝土的水化程度.

2 混凝土气体扩散模型

2.1 单根毛细管内的气体扩散系数

毛细管内的气体扩散系数与其可供气体扩散的有效空间有关［15］.在完全干燥的条件下，混凝土孔结构内的气体扩散空间最大，气体的扩散性能最好，但在具有一定相对湿度的环境中，由于水分的填充作用而导致毛细管中气体扩散空间减小，气体的扩散性能随水饱和度的增加而降低［16］.因此，获得考虑水饱和度影响的单根毛细管内气体扩散系数是建立混凝土中气体扩散系数模型的基础.

2.1.1 干燥条件下气体扩散系数

在干燥条件下，气体在毛细管中的扩散性能主要与其扩散形式有关，毛细管的管径是影响气体扩散形式的主要参数［15］.根据毛细管管径的不同，气体在干燥毛细管中的扩散形式分为两种：一种为较大管径中由气体分子间的碰撞形成主要阻力的体扩散，另一种为较小管径中由气体分子与孔壁之间的碰撞构成主要阻力的努森扩散［15］.气体在变截面单根毛细管中的扩散性能受体扩散和努森扩散的共同影响，因此，干燥条件下单根毛细管管径ri（x）处的扩散系数Dc［ri（x）］可表示为［16］：

式中：Dm，Dk［ri（x）］分别为气体的体扩散系数和努森扩散系数［15－16］，m2／s；R为理想气体常数，R＝8.314J／（mol·K）；KB为波尔兹曼常数，KB＝1.380 6×10－23J／K；T 为热力学温度，K；M 为气体的摩尔质量，kg／mol；p 为毛细管中的气体压强，Pa；σ为气体分子直径，m.

将式（8）中的孔深变量x 转换为毛细管管径变量r，并作为积分变量，再对各管径处气体扩散系数加权平均，可得到干燥条件下单根毛细管内的气体等效扩散系数Dc，i：

式中：Dc（r）为气体等效扩散系数，m2／s，可按式（1），（6）确定；x′i（r）为单根毛细管管径r 处斜率的倒数，可由式（1）得到.

2.1.2 湿润条件下气体扩散系数

为了分析一定相对湿度环境下毛细管中水饱和度对气体扩散性能的影响，根据基本假定（3），水分按一定厚度δi均匀分布在管道的内壁上，如图2所示.则气体在变截面毛细管中的有效扩散孔径rg，i（x）为：

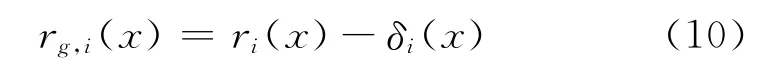
式中：δi（x）为孔深x 处的水分吸附厚度，m.

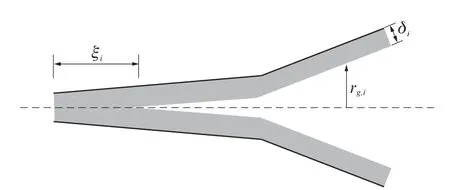
图2 湿润条件下变截面毛细管通道示意图Fig.2 Illustration of wet capillary with variable cross－section

气体在液体中的扩散速度远远小于其在空气中的扩散速度（一般相差4个数量级左右），因此可忽略气体在吸附水中的扩散，而只考虑气体在有效扩散空间中的扩散［9］.然而，当水分在变截面毛细管的较小管径截面处形成填充，则有效扩散空间消失，气体分子只能通过由水分子形成的水幕进行扩散，气体在液体中的扩散不可忽略.为了考虑不同水饱和度所形成的水幕对气体扩散性能的影响，引入水幕长度参数ξi来表征水饱和度的影响，如图2所示，则湿润条件下变截面毛细管中的气体等效扩散系数Dc，i（s）为：

式中：Dl为水中的气体扩 散系数，m2／s；Dc，i为气体在有效扩散空间中的扩散系数，m2／s.

2.2 混凝土中气体扩散系数

2.2.1 水幕长度与水饱和度之间的关系

变截面毛细管i中的水幕长度ξi 和水分厚度δi（x）是影响湿润条件下混凝土中气体扩散性能的重要参数，一般情况下难以通过实验测定.通过建立水饱和度s与水幕长度ξi 及水分厚度δi之间的关系，可获得具有一定水饱和度混凝土中的气体扩散系数.毛细管中的水分厚度δi和水幕长度ξi 与混凝土的水饱和度s之间的关系可按照以下两类条件来确定：

（1）当各毛细管内均未形成水幕，即毛细管内的水饱和度满足：

式中：Vi为变截面毛细管i的体积，m3.此时，毛细管内任意孔深x 处的水分厚度δi（x）相等，均为δi，则水幕长度ξi 和水分厚度δi与水饱和度s的关系为：

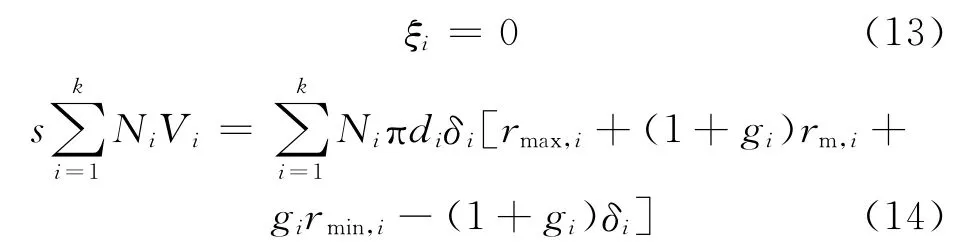
（2）当毛细管内产生水幕，且水幕在子毛细管束中从小管径到大管径依次形成，即毛细管内的水饱和度满足：

且第n类子毛细管束开始产生水幕时，其水幕长度与水饱和度之间的关系存在以下3种情况：

①当i≠n时：

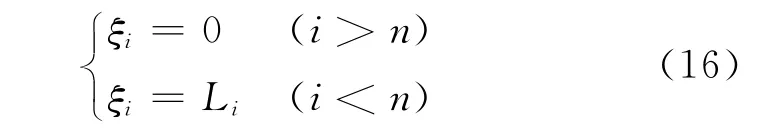
②当i＝n且水分在孔径≤rm，i处形成水幕时：

③当i＝n且水分在孔径＞rm，i处形成水幕时：

根据满足情况①～③的水幕长度ξi，并结合毛细管束内水分润湿特征，可得到毛细管在不同孔深x 处的水分厚度δi（x）：

式（12）～（19）是一个复杂的多元多次非线性方程组，通过数值迭代求解，可获得一定水饱和度条件下毛细管束模型中的水幕长度，相关计算过程可通过MATLAB编程实现.

2.2.2 气体等效扩散系数模型

根据基本假定（1），考虑水饱和度影响的混凝土中气体等效扩散系数De为：

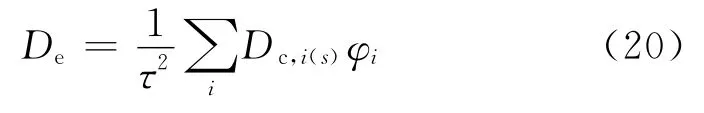
3 模型验证及参数分析

3.1 模型验证

为了验证所建立的混凝土气体扩散模型的合理性，运用Matlab 语言编制了该模型的计算分析程序.该程序可计算考虑水饱和度影响的气体等效扩散系数De，并分析气体种类、水饱和度、环境温度、材料组成及孔结构特征等参数对混凝土中气体扩散性能的影响规律.图3给出了水灰比（质量比，下同）为0.45的水泥净浆中氢气扩散系数随水饱和度的变化规律，其中，实测值取自文献［7］.从图3可以看出，氢气在水泥净浆中的扩散系数计算值随水饱和度的变化规律与实测值较为一致.表1给出了氧气在水灰比为0.35的混凝土中扩散系数的模型计算值和实测值，其中，计算模型中根据压汞法获得的混凝土孔结构分形维数取自文献［4］，文献［4］中混凝土水灰比为0.35，砂率（质量分数）为0.36，其中1m3混凝土中水泥、水、砂子、石子和减水剂的用量分别为420，147，667，1 186，3.36kg.氧气在混凝土中扩散系数的实测值取自文献［8］，孔结构模型的主要参数取自文献［7］，如表2所示.从表1可以看出，氧气在混凝土中的扩散系数计算值与实测值较为一致.

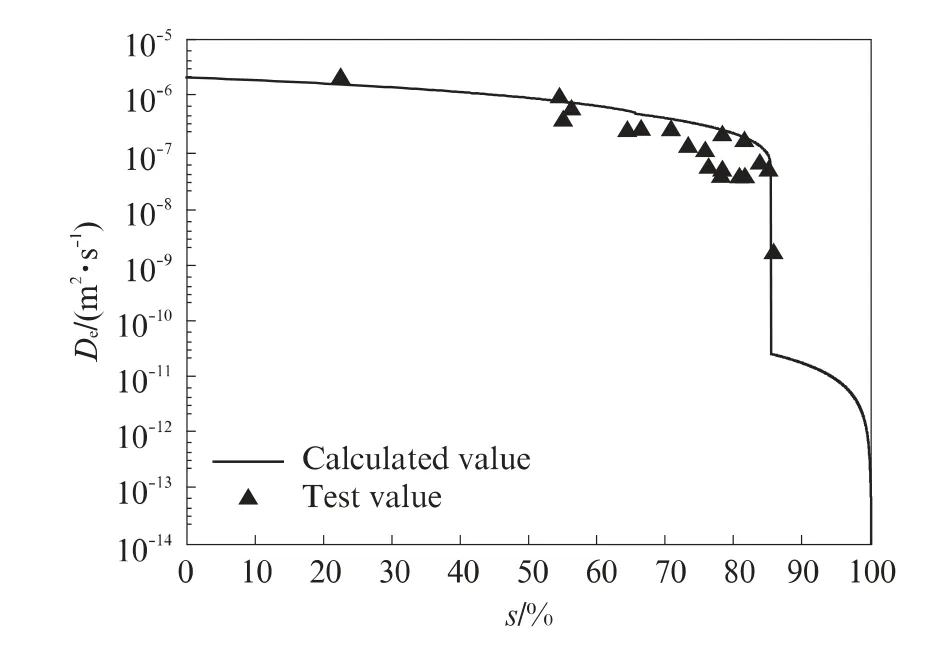
图3 水泥净浆中氢气扩散系数随水饱和度的变化Fig.3 Diffusion coefficient of hydrogen for cement paste at different water saturations

表1 氧气在混凝土中的扩散系数Table 1 Diffusion coefficient of oxygen in concrete

表2 孔结构模型的主要参数Table 2 Main parameters of pore structure model

3.2 气体扩散系数的影响因素

图3～6分别给出了气体扩散系数与水饱和度、气体摩尔质量、混凝土水灰比（分形维数）和环境温度的关系.从图3可以看出，氢气在水泥净浆中的扩散系数（模型计算值）随着水饱和度的增加而减小：当水饱和度从0%增至约80%时，氢气扩散系数从2.1×10－6m2／s降至1.9×10－7m2／s；当水饱和度达到85%时，氢气扩散系数突降至2.47×10－11m2／s，此时混凝土中的孔空间（孔径小于临界孔径29.78nm的孔隙）全部被水分填充至完全饱和，气体只能在连通性差的孔空间和孔溶液中缓慢扩散；水饱和度达到100%时，氢气扩散系数则降至1.1×10－13m2／s，此时氢气在水泥净浆中的扩散主要是在孔溶液中的扩散.从图4可以看出，气体扩散系数随气体摩尔质量的增大而减小，气体的摩尔质量越大，其布朗运动越慢，在孔结构空间中的扩散速度就越小，从而导致混凝土中气体扩散系数降低.图5表明，气体的扩散系数随着水灰比的增加而增大，随分形维数的增加而减小，当水灰比从0.35增加到0.65（或分形维数从2.963 5减小到2.906 0）时，3种气体扩散系数均增大约5倍.分形维数是综合表征混凝土孔结构特征的参数，材料的水灰比越大，对应的分形维数越小，则孔结构中可供气体扩散的有效空间越大，气体扩散速度就越快.从图6可以看出，环境温度也是影响气体扩散系数的因素之一，随着环境温度的升高，气体扩散系数增大.综上可知，混凝土的水饱和度和水灰比（分形维数）是影响气体扩散性能的主要参数.

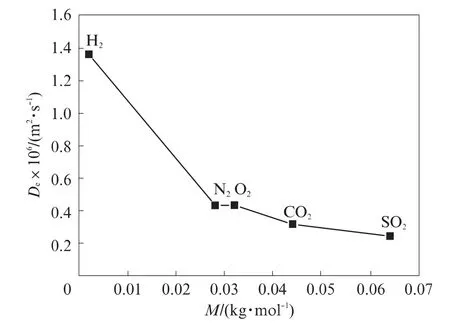
图4 气体扩散系数与气体摩尔质量的关系Fig.4 Relationship between diffusion coefficient and gas molar mass

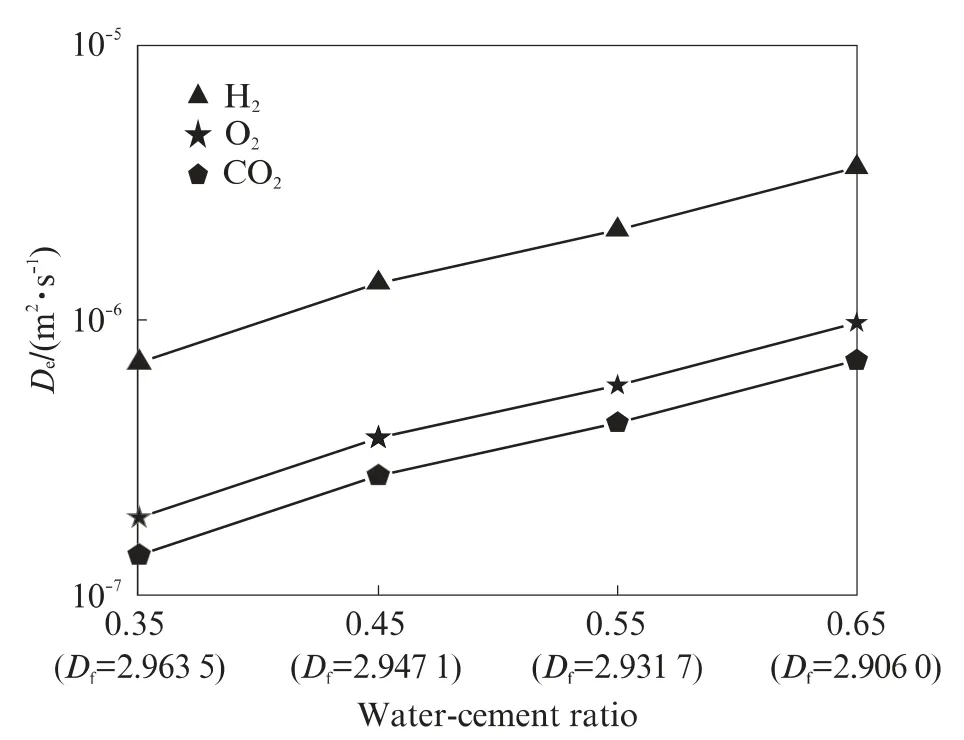
图5 气体扩散系数与混凝土水灰比（分形维数）的关系Fig.5 Relationship between diffusion coefficient and water－cement ratio（fractal dimension）

图6 气体扩散系数与环境温度的关系Fig.6 Relationship between diffusion coefficient and ambient temperature

4 结论

建立了运用分形维数来表征混凝土孔结构特征的毛细管束模型，并用该模型建立了考虑水饱和度影响的混凝土气体扩散模型，分析了气体种类、水饱和度、水灰比和环境温度对气体扩散系数的影响规律，其中混凝土的水灰比（分形维数）和水饱和度是影响混凝土气体扩散系数的主要因素.所建立的气体扩散模型可用于进一步分析大气环境中因二氧化碳、氧气等气体扩散引起的混凝土结构耐久性退化问题.

［1］许晨，岳增国，金伟良，等.碳化环境中混凝土钢筋锈蚀速率监测研究［J］.建筑材料学报，2012，15（4）：527－532，552.XU Chen，YUE Zengguo，JIN Weiliang，et al.Study on the real－time dynamic monitoring of corrosion rate of reinforcement in carbonation environment［J］.Journal of Building Materials，2012，15（4）：527－532，552.（in Chinese）

［2］牛荻涛，陈立亭，张成中.混凝土中气体扩散系数的计算模型［J］.西安建筑科技大学学报：自然科学版，2007，39（6）：741－745.NIU Ditao，CHEN Liting，ZHANG Chengzhong.Calculating model for gas diffusivity in concrete［J］.Journal of Xi'an University of Architecture ＆Technology：Natural Science，2007，39（6）：741－745.（in Chinese）

［3］耿欧，袁迎曙，朱辉，等.混凝土氧气扩散性能的预测模型［J］.中国矿业大学学报，2010，39（4）：471－474.GENG Ou，YUAN Yingshu，ZHU Hui，et al.Predicting oxygen diffusion in concrete［J］.Journal of China University of Mining ＆Technology，2010，39（4）：471－474.（in Chinese）

［4］韦江雄，余其俊，曾小星，等.混凝土中孔结构的分形维数研究［J］.华南理工大学学报：自然科学版，2007，35（2）：121－124.WEI Jiangxiong，YU Qijun，ZENG Xiaoxing，et al.Fractal dimension of pore structure of concrete［J］.Journal of South China University of Technology：Natural Science，2007，35（2）：121－124.（in Chinese）

［5］PAPADAKIS V G，VAYENAS C G，FARDIS M N.Physical and chemical characteristics affecting the durability of concrete［J］.ACI Materials Journal，1991，88（2）：186－196.

［6］ODEH A M，ABU－EL－SHA'R W，AL－RUZOUQ R.Gas transport through concrete slabs［J］.Building and Environment，2006，41（4）：492－500.

［7］BOTHER C，FRIZON F，LORENTE S，et al.Influence of the pore network on hydrogen diffusion through blended cement pastes［J］.Cement ＆Concrete Composites，2013，37：30－36.

［8］耿欧，袁迎曙，朱辉，等.混凝土氧气扩散系数试验研究［J］.东南大学学报：自然科学版，2006，36（S2）：191－194.GENG Ou，YUAN Yingshu，ZHU Hui，et al.Experimental study on diffusion coefficient of oxygen in concrete［J］.Journal of Southeast University：Natural Science，2006，36（S2）：191－194.（in Chinese）

［9］鲁彩凤，袁迎曙，蒋建华.粉煤灰混凝土孔隙结构对气体扩散能力的影响［J］.中国矿业大学学报，2011，40（4）：523－539.LU Caifeng，YUAN Yingshu，JIANG Jianhua.Effect of pore structure on gas diffusion in fly ash concrete［J］.Journal of China University of Mining ＆Technology，2011，40（4）：523－539.（in Chinese）

［10］李永鑫，陈益民，贺行洋，等.粉煤灰－水泥浆体的孔体积分形维数及其与孔结构和强度的关系［J］.硅酸盐学报，2003，31（8）：774－779.LI Yongxin，CHEN Yimin，HE Xinyang，et al.Pore volume fractal dimension of fly ash－cement paste and its relationship between the pore structure and strength［J］.Journal of the Chinese Ceramic Society，2003，31（8）：774－779.（in Chinese）

［11］郭伟，秦鸿根，陈惠苏，等.分形理论及其在混凝土材料研究中的应用［J］.硅酸盐学报，2010，38（7）：1362－1368.GUO Wei，QIN Honggen，CHEN Huisu，et al.Fractal theory and its applications in the study of concrete materials［J］.Journal of the Chinese Ceramic Society，2010，38（7）：1362－1368.（in Chinese）

［12］YU Boming，LI Jianhua.Some fractal characters of porous media［J］.Fractals，2001，9（3）：365－372.

［13］YU Boming.Fractal character for tortuous stream tubes in porous media［J］.Chinese Physics Letters，2005，22（1）：158－160.

［14］YU Boming，LI Jianhua.A geometry model for tortuosity of flow path in porous media［J］.Chinese Physics Letters，2004，21（8）：1569－1571.

［15］WELTY J R，WICKS C E，WILSON R E.Fundamentals of momentum，heat，and mass transfer［M］.2nd ed.Chichester，Sussex，UK：Wiley，1976：309－330.

［16］VU T H，FRIZON F，LORENTE S.Architecture for gas transport through cementitious materials［J］.Journal of Physics D：Applied Physics，2009，42（10）：1－9.