基于GEP算法的沥青混合料动模量预测

颜可珍，刘 沛，王晓亮

（湖南大学 土木工程学院，湖南 长沙 410082）

沥青混合料动模量是沥青路面结构设计和分析的重要参数之一［1］.如何确定沥青混合料的动模量已引起广大道路工作者的关注［2］.目前，确定沥青混合料动模量主要采用室内试验方法，但室内试验存在试样制备过程复杂、试验设备昂贵、费时费材料等缺点［3］.有学者提出通过离散元法的虚拟试验来确定沥青混合料的动模量［4］，但虚拟试验的细观参数确定困难.近年来神经网络等智能方法在材料性能预测方面取得了较好的效果.Ceylan等［5］采用神经网络方法对沥青混合料动模量进行了预测，Gopalakrishnan等［6］提出了基于支持向量机的沥青混合料动模量预测模型.以上方法虽然简单，精度也能满足要求，但并不能明确沥青混合料动模量与各因素间的内涵，无法得到明确的解析表达式，给应用带来了不便.

基因表达式编程（GEP）算法是一种新近发展的进化方法，可以实现多维空间上的数据挖掘.在复杂的非线性问题上，GEP算法是目前最有效的分析手段.近年来GEP 算法在岩土工程等领域被广泛应用，取得了很好的成果［7］.本文通过GEP 算法建立了沥青混合料动模量的预测模型，对多种沥青混合料进行预测，分析了预测结果的精度，并与人工神经网络等其他模型进行了比较.

1 基因表达式编程算法

1.1 基因表达式

GEP算法是一种基于生物基因结构和功能而发明的新型自适应演化算法，是从遗传算法（genetic algorithms，GAS）和遗传程序设计（genetic programming，GP）中发展而来.它克服了GAS系统中功能的复杂性及GP系统中遗传操作难的不足，具有更强的函数发现能力与更高的搜索效率.其显著特点是可以利用简单的编码解决复杂问题，其实质是用广义的层次转化为计算机程序来描述问题［8］.

1.2 GEP的基因结构

GEP算法中染色体为待解决问题的可行解，它由一个或多个基因组成固定长度的线性符号串构成.基因是构成染色体的基本单位.基因由头部和尾部构成，头部的符号可以是函数符号，也可以是终端符号，而尾部的符号只能来自于终端符号集.对具体问题而言，基因的头部长度根据问题需要选定，尾部长度则由头部长度与n 的一个函数得到，其中n 为基因含有的函数中最大参数的个数（对于加法等算术运算，n取2；对于三角函数、对数函数，n取1）.设基因的头部长度为h，尾部长度为e，基因含有的函数集中所有函数的最大操作数为n，则e＝h×（n－1）＋1，其表现形式是一棵基因表达式树，它可由基因型按照语法规则和层次顺序构成，基因型将表达式树的变量按照从上往下、从左至右的顺序进行排列.每个染色体由单个或多个基因组成，每个基因确定一棵子表达式树，而多个子树可由函数符相互连接［9－10］.例如，假定一个基因是由集合｛q，×，／，－，＋，x，y｝中的元素组成（其中q表示根号），则n＝2，若h＝10，则e＝11，从而基因的长度为21；基因型如下（其中黑体部分为其尾部）：

其对应的表达式树见图1.图1的语义即为：

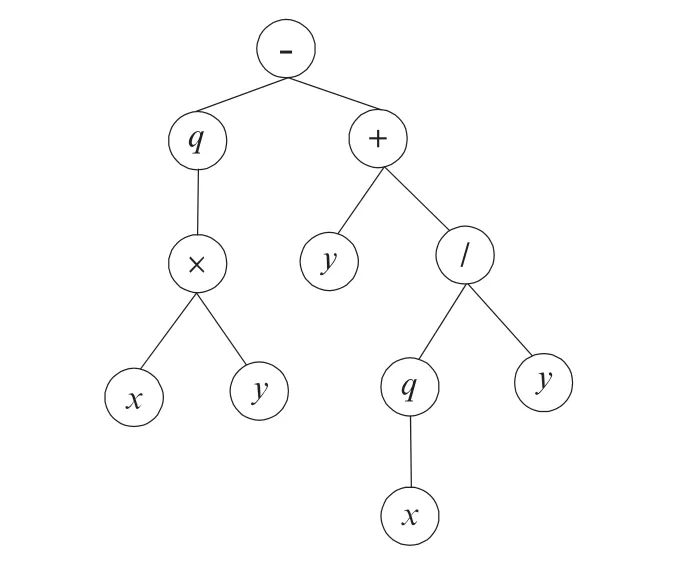
图1 基因型对应的表达式树Fig.1 Genotype correspond to the expression tree

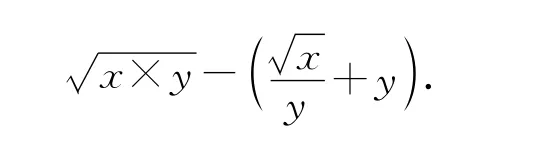
2 基于GEP 算法的沥青混合料动模量预测模型

2.1 影响因素分析

根据沥青混合料材料组成与动模量的影响因素，结合有关研究成果［11－12］，本文拟采用影响动模量的8个主要因素为预测模型的输入变量，它们是：沥青混合料空隙率（体积比）Va；有效沥青含量（质量比）wbeff；集料在19，9.5，4.75mm 筛孔上的筛余质量分数ρ34，ρ38，ρ4；在0.075mm 筛孔上的通过率（质量分数）ρ200；沥青黏度η（MPa·s）；荷载频率f（Hz）.以马里兰大学沥青研究所在过去30 年对205种沥青混合料进行实验室测试所建立的2 750组数据点作为应用GEP 算法及评价模型的数据基础［11］，每个影响因素的取值范围、沥青混合料动模量E 的实测值以及它们的离散性如表1所示.

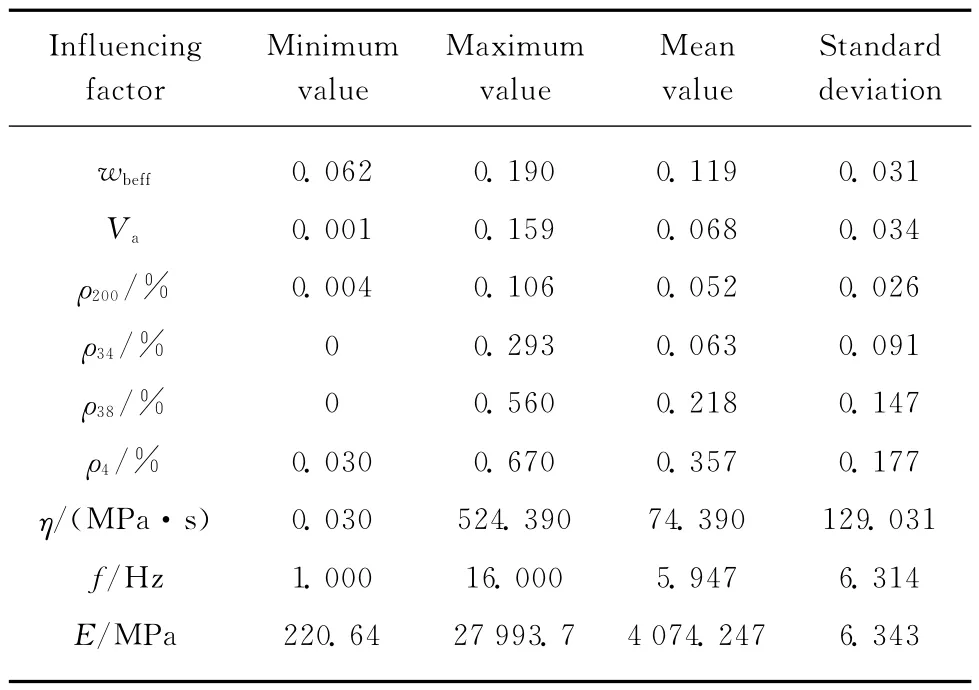
表1 8个影响因素和动模量实测值的离散情况Table 1 Discrete case of eight influencing factors and dynamic modulus measured values

2.2 沥青混合料动模量预测模型的求解流程

根据GEP算法原理，可以得到沥青混合料动模量预测模型的求解流程，如图2所示.

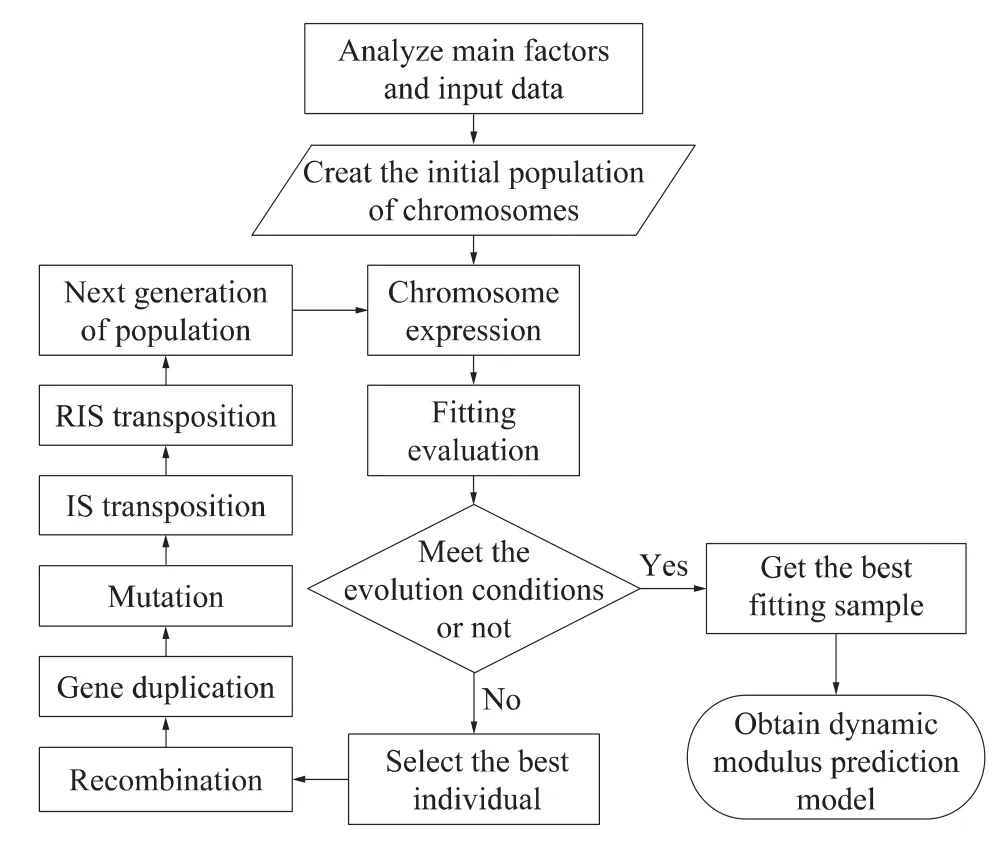
图2 沥青混合料动模量预测模型的流程图Fig.2 Flowing chart of prediction model for dynamic modulus of asphalt mixture

对于沥青混合料动模量预测模型优劣性的评估，采用统计学中的相关系数R、拟合度R2以及实测值和预测值的标准误差Se与实测值标准误差Sy之比Se／Sy作为评价标准［12］.

3 GEP算法的预测结果及比较分析

3.1 GEP算法预测沥青混合料动模量模型

3.1.1 确立动模量预测模型

根据GEP算法原理，建立预测模型时先将数据库随机划分为两大部分：第一部分为训练组，有2 000组数据，占总数据的72.7%；第二部分为验证组，有750 组数据，占总数据的27.3%.运用GEP算法对2 000组数据进行反复训练之后，得出最佳适应度样本的染色体，即沥青混合料动模量预测模型，再将预测模型放在验证组的750组数据中进行拟合度验证.

运用GEP算法确定动模量预测模型的第一步是确定GEP算法的进化参数.通过分析GEP算法特性可知，基因数量范围在［3，6］之间，种群大小范围在［30，100］之间，进化代数大于10 000代时能够找到最优染色体.本文在对GEP算法进行反复试算后确定种群大小为50，基因数量取6，基因头部长度取12，进化代数为100 000代.第二步是选择终点符集T 和函数集F.终点符集T为动模量8个影响因素，T＝｛A1，A2，A3，A4，A5，A6，A7，A8｝；函数集选取没有参考依据，通过反复试算，最后确定最优函数集F＝｛＋，－，×，／，＾2，lg｝.第三步是选取连接函数，此处选择“＋”作为基因之间的连接函数.第四步是遗传算子设计.综合变异、转座、重组算子，设置算子参数值如下：变异率0.044，IS 转座率0.1，RIS 转座率0.3，基因转座率0.3，单点重组率0.1，两点重组率0.1，基因重组率0.1.由GEP算法强大的函数挖掘能力，经过反复计算后得到较好的动模量预测模型为：

3.1.2 GEP预测模型结果的分析

将预测模型得到的动模量预测值与实测结果进行比较，分别列出训练组、验证组及整个数据库预测值与实测值的相关性，见图3.由图3可知，训练组中R2＝0.941，Se／Sy＝0.137；验证组R2＝0.906，Se／Sy＝0.264；整体样本数据组R2＝0.925，Se／Sy＝0.168.当拟合度R2≥0.90，误差比值Se／Sy≤0.35时，表明预测值与实测值相关性很好［11］.因此用GEP预测模型来预测沥青混合料动模量时具有很好的拟合度，能满足工程上的精度要求，具有可行性.

图3 动模量模型预测值与实测值的相关性及拟合度Fig.3 Correlation between predicted values and measured values of dynamic modulus

3.2 GEP算法预测模型与现有模型比较分析

将GEP算法预测模型与现有的3个代表性沥青混合料动模量预测模型：Witczak 1999函数模型、韩国动模量预测模型及人工神经网络（ANN）模型［5，12］进行比较分析.Witczak 1999函数模型见式（2）；韩国预测模型采用西格谟得函数对多种沥青混合料数据进行非线性分析，得到的预测模型见式（3）［13］.这几种模型所用的变量参数均相同（即动模量的8个影响因素）.运用相同的数据库作为输入变量，计算出各个模型的动模量预测值，并分别与实测值进行比较，分析动模量预测值与实测值的相关性，结果如图4所示.对4种动模量模型预测值与实测值之间的相关性进行对比分析，见表2.

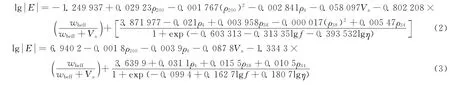
图4 动模量预测值与实测值的相关性Fig.4 Correlation between predicted values and measured values of dynamic modulus

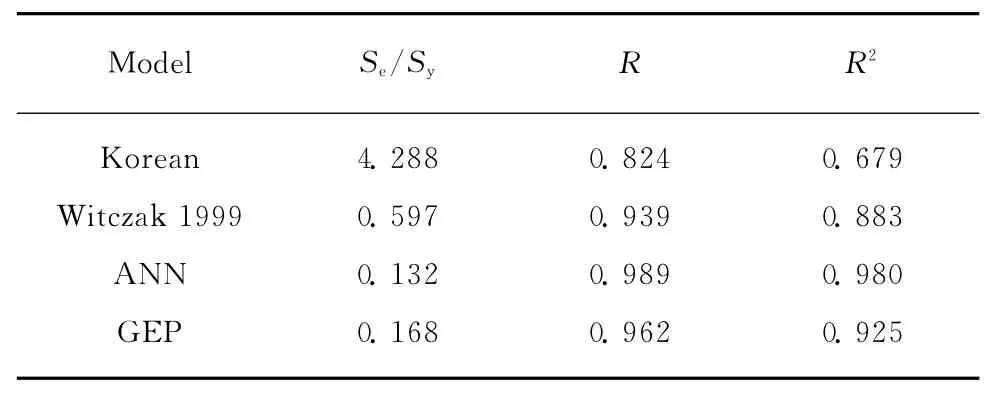
表2 4种模型预测值与实测值之间的误差和相关性对比分析Table 2 Comparative analysis of the correlation and error between predicted values and measured values of four models

由表2可知，GEP算法的拟合度达到了0.925，精度高于Witczak 1999预测模型和韩国预测模型，但比人工神经网络模型略低.虽然人工神经网络模型预测精度比GEP算法略高，但人工神经网络模型的隐含层层数及隐含层节点数目前尚无很好的确定方法，很难找到最优的参数组合，而且神经网络方法是一种黑匣子计算方法，不能得到预测因子的显式表达式，无法明确各预测因素与被预测因子间关系［14］.GEP算法模型简单，能得到函数的显式表达式，运用方便，为沥青混合料动模量预测提供了一种新的方法.

3.3 8个影响因素对动模量预测的敏感性分析

根据皮尔森相关系数的原理，进行动模量影响因素敏感性分析［15］.选定1个影响因素作为输入变量参数，其他输入参数不变，预测输出参数.皮尔森相关系数定义式为：

式中：N 为样本量；Xi，Yi为选定的输入变量参数和输出参数；分别为输入参数和输出参数的平均值；SX，SY分别为输入参数和输出参数的标准差.

将8个影响因素与动模量的敏感性分析结果用柱状图表示，见图5.由图5 可知，Witczak 1999，ANN，GEP预测模型与动模量实测值对各影响因素具有相似的相关性，其中与动模量实测值正相关的影响因素有骨料级配特性ρ200，ρ34，ρ38，ρ4 以及沥青黏度η和荷载频率f；负相关影响因素为有效沥青含量wbeff和沥青混合料空隙率Va.韩国预测模型中与动模量实测值正相关的影响因素有ρ200，η，f；具有负相关的影响因素为wbeff，Va，ρ34，ρ38，ρ4.

图5 各影响因素对动模量的敏感性分析Fig.5 Sensitivity analysis of each factor on the dynamic modulus

由此可知，GEP模型、ANN 模型、Witczak 1999模型与动模量实测值对各影响因素的敏感性具有较好的一致性，而韩国预测模型中各影响因素的敏感性与实际情况偏差较大.

4 结论

（1）根据GEP算法建立的动模量预测模型精度高，能得到预测因子与各影响因素的显式函数表达式，可以准确预测沥青混合料的动模量值.

（2）与其他典型预测模型相比，GEP模型预测精度优于Witczak 1999预测模型和韩国预测模型，略低于人工神经网络模型，但人工神经网络模型不能得到函数的显式表达式，无法明确各预测因素与被预测因子间关系.因此，GEP模型在保证预测精度的同时有效克服了人工神经网络等传统方法的不足，从而为沥青混合料动模量的预测提供了一种新的可靠方法.

［1］韦金城，崔世萍，胡家波.沥青混合料动模量试验研究［J］.建筑材料学报，2008，11（6）：657－662.WEI Jincheng，CUI Shiping，HU Jiabo.Research on dynamic modulus of asphalt mixtures［J］.Journal of Building Materials，2008，11（6）：657－662.（in Chinese）

［2］陈少幸，虞将苗，李海军，等.沥青混合料模量不同测试方法的比较分析［J］.公路交通科技，2008，25（8）：6－10.CHEN Shaoxing，YU Jiangmiao，LI Haijun，et al.Comparative analysis of different test methods on asphalt mixture modulus［J］.Journal of Highway and Transportation Research and Development，2008，25（8）：6－10.（in Chinese）

［3］耿立涛，杨新龙，任瑞波，等.稳定型橡胶改性沥青混合料动模量预估［J］.建筑材料学报，2013，16（4）：720－725.GENG Litao，YANG Xinlong，REN Ruibo，et al.Dynamic modulus prediction of stabilized rubber modified asphalt mixtures［J］.Journal of Building Materials，2013，16（4）：720－725.（in Chinese）

［4］田莉.基于离散元方法的沥青混合料劲度模量虚拟试验研究［D］.西安：长安大学，2008.TIAN Li.The virtual test of asphalt mixture stiffness moduli based on DEM［D］.Xi'an：Chang'an University，2008.（in Chinese）

［5］CEYLAN H，SCHWARTZ C W，KIM S，et al.Accuracy of predictive models for dynamic modulus of hot－mix asphalt［J］.Journal of Materials in Civil Engineering，2009，21（6）：286－293.

［6］GOPALAKRISHNAN K，KIM S.Support vector machines approach to HMA stiffness prediction［J］.Journal of Engineering Mechanics，2011，137（2）：138－146.

［7］刘昌辉.基因表达式编程在边坡稳定性分析中的应用［D］.武汉：中国地质大学，2008.LIU Changhui.Gene expression programming in slope stability analysis［D］.Wuhan：China University of Geosciences，2008.（in Chinese）

［8］FERRIRA C.Gene expression programming：A new adaptive algorithm for solving problems［J］.Complex Systems，2001，13（2）：87－129.

［9］FERREIRA C.Gene expression programming：Mathematical modeling by an artificial intelligence［M］.2nd ed.Berlin：Spring－Verlag，2006：25－67.

［10］元昌安，彭昱忠，覃晓，等.基因表达式编程算法原理与应用［M］.北京：科学出版社，2010：25－30.YUAN Chang'an，PENG Yuzhong，QIN Xiao，et al.Principles and applications of gene expression programming algorithm［M］.Beijing：Science Press，2010：25－30.（in Chinese）

［11］ANDEI D，WITCZAK M W，MIRZA W.Development of a revised predictive model for the dynamic（complex）modulus of asphalt mixtures［M］.Illinois：National Cooperative Highway Research Program—Transportation Research Board National Research Council，2001：108－204.

［12］CEYLAN H，GOPALAKRISHNAN K，KIM S.Looking to the future：The next－generation hot mix asphalt dynamic modulus prediction models［J］.International Journal of Pavement Engineering，2009，10（5）：341－352.

［13］CHO Y－H，PARK D－W，HWANG S－D.A predictive equation for dynamic modulus of asphalt mixtures used in Korea［J］.Construction and Building Materials，2010，24：513－519.

［14］YAN Kezhen，XU Hongbin，SHEN Guanghui.Novel approach to resilient modulus using routine subgrade soil properties［J］.International Journal of Geomechanics，ASCE，ISSN 1532－3641／04014025（9）.

［15］GOPALAKRISHNAN K，KIM S.Support vector machines approach to HMA stiffness prediction［J］.Journal of Engineering Mechanics，2011，137（2）：138－146.