油底壳有限元模态分析及实验验证
2015-11-28孙杰绳锴尹长城张继伟
孙杰,绳锴,尹长城,张继伟
(湖北汽车工业学院汽车工程学院,湖北十堰442002)
以EQ491型发动机为载体,采用BBM 数据采集系统以及LMS的模态分析软件,验证发动机油底壳有限元模型自由模态的准确性。以此为依据,对油底壳约束模态进行有限元分析,分析对比油底壳约束模态的固有频率和油底壳与机体发生共振的频率,验证结构设计的合理性。

图1 EQ491型发动机油底壳三维模型
1 有限元模型建立
1.1 建立CAD模型
采用Catia软件建立EQ491发动机油底壳的三维模型,几何模型如图1所示。
1.2 建立有限元模型
将油底壳几何模型导入到Hypermesh中,对原始CAD模型进行一些必要的简化处理:首先在Hypermesh中对模型抽取中性面,然后对几何模型进行一些简要的几何清理,如圆角、密封槽等,这样能提高网格划分的质量和速度,同时减少计算误差。有限元单元的相关参数设定具体如表1所示。
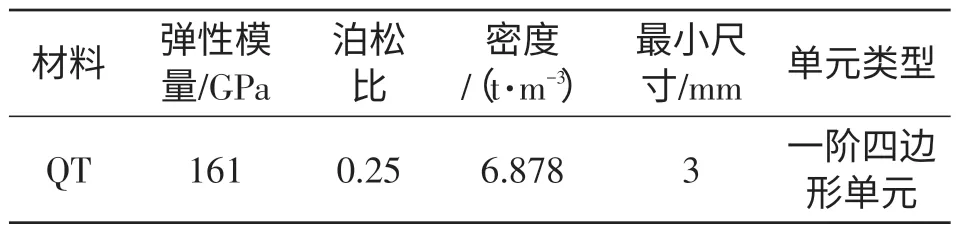
表1 有限元模型相关参数
对模型进行网格剖分,最终得到的有限元模型由29903个单元,29994个节点组成。网格为四节点四边形壳单元,网格单元厚度为实物模型的厚度1.5 mm。网格剖分完成后的有限元模型见图2。

图2 油底壳有限元模型
2 实验模态介绍
2.1 试验支撑和测点布置
试验结构的边界条件是要考虑的重要因素,不同的边界条件的结构特性可能完全不同。本实验是测油底壳的自由模态。因此对待测物应采用尽量软的物体进行支撑,即具有较低的支撑刚度和阻尼。本实验中油底壳采用橡皮绳悬挂,虽然刚体模态频率不再是零,但如果刚体模态最高频率小于结构最低弹性模态固有频率的1/3时,则认为该模型处于自由悬挂状态。
试验测点尽量均布在油底壳结构上,能够表示油底壳的形貌。该模型共布置了61个测点,全部分布在油底壳的外表面(图3)。

图3 试验测点分布图
2.2 试验方法
由于油底壳体积较小,本试验采用力锤敲击法进行实验。对于不同的试件,会有不同的响应测试范围,而对试件频响带宽造成最直接影响的因素是锤击力的频带宽度,影响力脉冲宽度的主要因素为锤头硬度、力锤质量和试件刚度。本实验试件刚度不可变,只能改变锤头刚度和力锤质量来控制力脉冲的宽度。该实验使用500 N的力锤,锤头材料为PVC。经实验验证,采用500 N、材料为PVC锤头的力锤敲击,能激出该油底壳的所有模态。
本试验采用单点激励,针对61个测试点进行逐点激励。
2.3 实验原理
根据振动理论,只需要获得油底壳的频响函数矩阵,即可得到结构的模态参数。在工程上,通常只需要频响函数矩阵的任意一个元素即可;而要获得一组完整的模态振型,必须求出频响函数矩阵中的一列或一行元素。由频响函数的物理意义可知,传感器的信号响应与力锤的激励信号之比即为所需的频响函数。
在对模型进行模态分析时,实际构件是一个连续的系统(无限多自由度)。工程上在进行分析时,通常将构件看成是质点、刚体、弹性体和阻尼组成的系统,并将构件离散成有限多个相互弹性连接的刚体,将连续系统的振动转化成多自由度系统的振动,从而简化计算模型。假设系统满足定常线性系统的要求,则系统的数学模型可用式(1)表示:
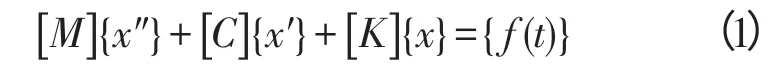
式中:[M]为质量矩阵;[C]为阻尼矩阵;[K]为刚度矩阵;{x}为位移;f(t)为作用力。
式(1)方程是互相耦合的,将式(1)进行坐标变换,使用模态坐标可以让式(1)变换成模态解耦方程,在新坐标系中,固有频率、阻尼、质量、刚度等被称为模态参数。
2.4 实验参数的设置
1)平均次数的设置
一是明确专项工作包联主体。项目引进之后,党委政府明确牵头领导和责任单位,将辖区管理和职能部门有效连接,给予回乡创业项目全面、实时、无缝的服务,尽最大努力协调解决项目遇到的困难。二是加强基础设施建设力度。地方党委政府加快推进农村路网、管网、电网、通信网等基础设施建设,为回乡项目提供硬件条件支持。三是督促项目规范有序运作。地方党委政府除了服务项目运作,还积极担负起监督项目规范运作的职责,督促企业规范运用各类优惠政策,遵纪守法、安全生产,做好相关职工维权和矛盾调处工作,真正确保项目健康运作、良性发展。
为了减小外部噪声对实验产生的影响,FRF测量需作多次谱平均。理论上讲,平均的次数越多,得到的FRF 数据可信度越高。但过多的平均次数会使敲击工作量加大。为了节省时间,且兼顾FRF质量,本次实验取5次进行平均。[1]
2)采样频率的设置
在对频率进行拾取的过程中,为防止频率混叠现象的发生,采样定理要求采样频率大于最高频率的2倍,工程中一般设置采样频率为最高阶频率的2.56倍。油底壳有限元分析第4阶自由模态固有频率为343Hz,经计算,本次实验取采样频率为1500Hz。
3)相干系数的设置
相干系数是评价采集数据质量好坏的工具,它反映了激励和响应信号的相干关系。若相干系数等于1,说明响应信号完全由对应激励产生;若相干系数为0,说明实测响应信号与实测激励信号完全无关。相干关系与环境噪声、测点敲击力度及方向等因素有关。在共振区和反共振区,相干系数下降较多,属于正常现象。[2]因此在测量频响函数时,本试验需要同时测得相干函数。对敲击质量进行实时监测,使采集的数据尽量准确。在非共振区和非反共振区,本试验要求相干系数大于0.80。
3 模态验证
在对有限元模型进行约束模态分析之前,需要先验证有限元模型的准确性。首先对有限元模型进行自由模态分析,然后通过实验测出模型的自由模态固有频率。将试验模态和有限元模态固有频率及振型进行对比,比较两者结果的误差,若二者误差在10%以内,则说明建立的有限元模型非常准确,可以利用该有限元模型进行分析。[3]
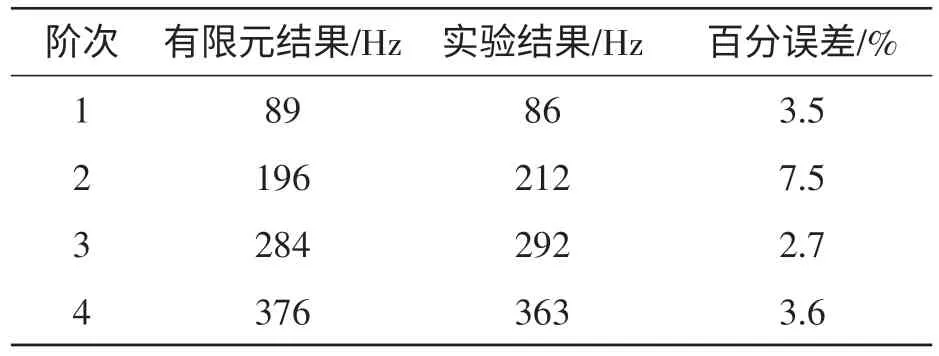
表2 有限元固有频率与实验固有频率对比
第1阶模态有限元模型的振型和试验模态的振型大体保持一致,其振动主要是4个角点的扭转振动,振型如图4所示。
第2阶模态有限元模型的振型和试验模态的振型基本保持一致,其振动主要是较长边侧面相向振动,振型如图5所示。
第3阶模态的振型主要是较长边的两侧面同向振动,振型如图6所示。
第4阶模态的振型主要是四角点上下振动,振型如图7所示。
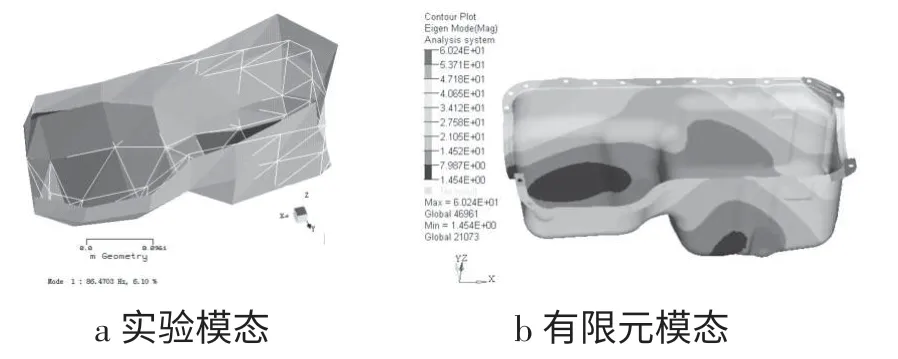
图4 第1阶自由模态振型
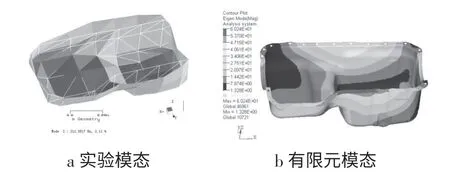
图5 第2阶自由模态振型

图6 第3阶自由模态振型

图7 第4阶自由模态振型
实验结果和有限元计算结果前4阶固有频率相差都在10%以内。并且各阶模态的振型基本一致。说明建立的有限元模型比较准确,可以进行后续约束模态分析。
4 约束模态分析
实际工况中,油底壳通过联接螺栓与机体连接。因此,约束模态有限元模型可简化为上表面螺栓孔周围节点被约束6个自由度,其他参数不改变。模型建立完成后,进行约束模态分析,取其前4阶固有频率的计算值及振型图,计算值如表3所示,振型如图8所示。
从约束模态的分析结果来看,油底壳受到外界激励作用时,主要变形区域集中在底板和两侧板上,这些部位容易与机体发生共振。
该油底壳搭载在四缸四冲程发动机上,机体与油底壳是否发生共振主要取决于发动机工作时的激振频率和油底壳的固有频率,只要两者相差较大就不会发生共振。发动机激振频率计算公式为

表3 约束模态各阶频率及振型描述

图8 约束模态振型

式中∶fi为发动机工作时的激振频率;i为气缸数;n为瞬时转速;τ为冲程数[4]。
EQ491型发动机怠速时转速约为750 r·min-1,最高转速约为5200 r·min-1,将转速代入式(2),计算得出该发动机激振频率为25Hz和174Hz,油底壳第1阶固有频率远大于机体激振频率。故该油底壳不会与机体发生共振,结构设计是合理的。
5 结论
本文中建立了油底壳有限元模型,通过对油底壳进行试验模态分析和有限元自由模态分析,验证了有限元模型建立的合理性。通过对有限元模型进行约束模态分析,与机体激振频率进行比较,验证了油底壳模型结构设计的合理性。
[1]庞剑,谌刚,何华.汽车噪声与振动理论与应用[M].北京:北京理工大学出版社,2006:69-76.
[2]吕永林,任丽娜.制动盘的试验模态与数值模态的分析与研究[J].湖北汽车工业学院学报,2012,26(1):73-76.
[3]王天利.基于LMS 实验的发动机油底壳优化研究[J].辽宁工业大学学报,2014(1):46-48.
[4]余志生.汽车理论[M].5版.北京:机械工业出版社,2006.
[5]尹长城,马迅,陈哲.基于ANSYS Workbench传动轴的模态分析[J].湖北汽车工业学院学报,2013,27(1):15-17+22.
