考虑异面交会因素的调炮精度数据处理方法
2015-11-27解文凯
王 媛,霍 李,赫 赤,解文凯,李 强
(中国白城兵器试验中心,吉林 白城 137001)
调炮精度是地面压制类火炮的重要战术技术指标,直接影响到武器系统的射击精度。调炮精度的检测过程实质上就是测量身管指向变化量的过程。由于用双经纬仪检测调炮精度具有操作简单、精度高的优点,目前在现场检测中已广泛采用双经纬仪交会测量方法[1-7]。为进一步提高该方法的检测精度,文献[7-8]从优化经纬仪布站的角度来进行研究。文献[1-8]都是假设2台经纬仪的视轴共面相交于目标点,但在现场操作中,由于受到经纬仪结构、测角精度及对目标观测位置差异等多种因素的影响,2台经纬仪的视轴很难实现真正意义上的共面相交,往往为异面关系。因此,用传统的数据处理方法解算得到的结果与实际情况并不完全吻合。
经纬仪异面交会的数据处理方法在动态目标跟踪测量领域已有广泛的研究,但相关文献[9-12]在测量点坐标的权系数选择上都只局限于经纬仪测角精度的影响,在等测角精度时目标估计点往往取公垂线中点。实际上,即使经纬仪的测角精度相同,但随着目标点与经纬仪的距离变化,空间点坐标的精度还是不同的。
笔者在双经纬仪检测调炮精度的数据处理中引入了文献[9]异面交会的思想,在测量点坐标权系数的选择上不仅考虑了经纬仪测角精度的影响,而且还考虑了经纬仪到目标点的距离变化的影响。该数据处理方法没有改变现场操作,为提高双经纬仪检测调炮精度提供了新思路。
1 传统双经纬仪调炮精度检测方法
1.1 双经纬仪交会测量原理
双经纬仪交会测量原理[13]如图1所示,2台电子经纬仪位于点O1和O2瞄准同一目标点S,2条视轴相交于点S,观测得到一组水平角和俯仰角(α1,β1,α2,β2),设基线O1O2的长度为l,则点S(x,y,z)的坐标可用式(1)表示。
反之,如果知道点S(x,y,z)的坐标,也可通过式(2)反算出经纬仪相应的观测角(α1,β1,α2,β2)。


从式(1)中可以看出,观测值β2并未参与点S(x,y,z)的坐标计算。这是一种常见的简化数据处理方法。
1.2 身管指向角的解算
如图2所示,A、B是身管上2个标记点,2台经纬仪对其观测角分别为A(α11,β11,α12,β12)和B(α21,β21,α22,β22),由式(1)可计算出点A(xA,yA,zA)和点B(xB,yB,zB)的坐标。
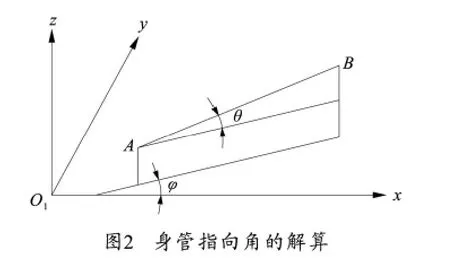
按文献[3]的思路,将点A(xA,yA,zA)和点B(xB,yB,zB)的坐标分别代入式(3)和式(4)可得到身管指向的方位角φ和高低角θ。

2 考虑异面交会因素的双经纬仪数据处理方法
在实际检测中,2台经纬仪的视轴往往并不相交,为异面关系,如图3所示。

在图3中,设经纬仪视轴所在的2条异面直线的公垂点分别为点P1和点P2,经纬仪的测角精度分别为σ1和σ2,基线O1O2的长度为l,经纬仪对目标点P(x,y,z)的观测角为(α1,β1,α2,β2),则 点O1(xo1,yo1,zo1)和 点O2(xo2,yo2,zo2)的坐标分别为(0,0,0)和(l,0,0)。
可列出2条视轴O1P1和O2P2的点向式方程,见式(5)。

根据异面直线和公垂线的垂直关系,由式(5)可得异面直线2 个公垂点P1和P2的坐标为Pi(xoi+licosαi,yoi+ (- 1)i+1lisinαi,zoi+(-1)i+1litanβi)。其中,li(i=1,2)为方程参数,其表达式为

在估计目标点P的坐标时,设置点P1的权系数为ρ,则点P2的权系数为1-ρ。按式(6)估计出目标点P(x,y,z)在公垂线上的位置。

根据式(6)计算出身管上2个标记点A和B的坐标,再代入式(3)和式(4)得到相应的身管指向的方位角φ和高低角θ。
文献[9-12]都是取ρ=0.5,为便于叙述称之为“公垂线中点法”。本文综合考虑到经纬仪的测角精度和经纬仪到目标点的距离这2个因素对目标空间点坐标精度的影响,权系数ρ按式(7)计算。

式中:d1为经纬 仪O1到目 标 点P1的 距 离;d2为 经纬仪O2到目标点P2的距离。
3 模拟分析
3.1 基于蒙特卡洛方法的测量精度评定步骤
步骤1:构建身管上2 个标记点的坐标,由式(3)和式(4)解算出身管指向的理想方位角φ0和理想高低角θ0,并通过式(2)计算出对应各点的经纬仪观测角理论值(α′1i,α′2i,β′1i,β′2i),其中i=1,2。
步骤2:根据经纬仪测角误差在概率上符合正态分布特征[14],即ε∈N(0,σ2),选取合适的经纬仪测角精度σ仿真出测量过程中经纬仪观测角的1组伪随机数(εα1i,εα2i,εβ1i,εβ2i),其中i=1,2。
步骤3:将经纬仪观测角理论值加上仿真出的经纬仪观测角的伪随机数,得到经纬仪测量过程的“伪观测角”

步骤4:将经纬仪的“伪观测角”分别代入式(1)和式(6),分别用传统的数据处理方法、公垂线中点法和本文方法解算出测量点的坐标,再代入式(3)和式(4)解算出2种方法的身管指向方位角和高低角各1组模拟样本。
步骤5:重复步骤2~4的过程m次,计算将得到传统方法、公垂线中点法和本文方法各m个方位角模拟样本(φi1,φi2,…,φim)和m个高低角模拟样本(θi1,θi2,…,θim),其中i=1,2。对样本进行统计,分别得到方位角和高低角的测量均方差δφi和δθi,如式(8)和式(9)所示。

步骤6:比较传统的数据处理方法、公垂线中点法和本文方法的身管指向的测量精度。
3.2 蒙特卡洛模拟分析
取2台经纬仪间的距离(基线)l=10m。假设在火炮身管上标记了2个点A和B,并赋予这2个点在经纬仪测量坐标系中的空间坐标A(1,6,3)和B(8,7,4),单位为m。此时,标记点A和B分别到2台经纬仪的距离也就确定了。
将点A和点B的坐标值分别代入式(3)和式(4),解算出2点连线理论上的方位角φ0 =8°7′48″、高低角θ0=8°2′59″。
通过式(2)计算出标记点A和B对应的经纬仪理论观测角(α′1i,α′2i,β′1i,β′2i),其中i=1,2,如表1所示。

表1 标记点的经纬仪观测角理论值
分别取经纬仪测角精度σ为2″、5″和8″,并考虑到2台经纬仪测角精度的异同情况,利用Matlab编程的方法随机抽样m=105次。分别用传统方法、公垂线中点法和本文方法进行数据处理,结果如表2所示。

表2 采用不同数据处理方法得到的测量结果
表2的结果表明,本文的数据处理方法无论是与传统数据处理方法相比还是与公垂线中点法相比均有显著提高。与传统方法相比,新方法的身管指向精度至少提高了3%,特别是经纬仪测角精度相同时,身管指向精度在高低方向甚至能提高23%以上;与公垂线中点法相比,即便是经纬仪测角精度相同,新方法的身管指向精度在方位和高低方向上分别提高了0.3%和2.9%以上。
4 结论
在双经纬仪交会测量调炮精度的数据处理中,考虑了异面交会因素对测量结果的影响,在对目标点位置估计时,不仅考虑了经纬仪测角精度对空间点坐标的影响,而且考虑了目标点到经纬仪的距离变化对空间点坐标精度的影响。模拟结果表明,在没有改变现场操作的情况下,本文数据处理方法也能显著提高检测精度,验证了该方法的可行性和有效性,为优化双经纬仪检测调炮精度方法提供了新思路。
(References)
[1]陶化成,张卫民,黄小平,等.压制兵器身管指向测试系统[J].测控技术,2001,20(8):20-22.TAO Huacheng,ZHANG Weimin,HUANG Xiaoping,et al.Aiming direction testing system of suppressing weapons[J].Measurement & Control Technology,2001,20(8):20-22.(in Chinese)
[2]吴飞雪,徐丽,韩有和.用双经纬仪进行调炮精度测量的精度分析[J].兵器试验,2004(3):15-21.WU Feixue,XU Li,HAN Youhe.Accuracy analysis of gun rotated precision survey with double theodolites[J].Ordnance Test,2004(3):15-21.(in Chinese)
[3]罗鸿飞,张英堂,任国全,等.基于空间坐标解算的火炮调炮精度检测方法研究[J].火炮发射与控制学报,2007(3):50-52.LUO Hongfei,ZHANG Yingtang,REN Guoquan,et al.Research on measuring method of gun rotated accuracy based on spatial coordinate algorithm[J].Journal of Gun Launch & Control,2007(3):50-52.(in Chinese)
[4]刁中凯,蒋永谕.火炮调炮精度检测技术[J].四川兵工学报,2008,29(2):48-50.DIAO Zhongkai,JIANG Yongyu.Gun rotated precision detection technology[J].Journal of Sichuan Ordnance,2008,29(2):48-50.(in Chinese)
[5]李平,王英.基于数字式经纬仪检测的调炮精度测量装置[J].火力与指挥控制,2010,35(增刊1):96-98.LI Ping,WANG Ying.Gun slaving accuracy measurement unit based on digital theodolite detect[J].Fire Control &Command Control,2010,35(Sup1):96-98.(in Chinese)
[6]曾刊,赖文娟.双经纬仪调炮精度检测系统[J].兵工自动化,2011,30(7):73-75.ZENG Kan,LAI Wenjuan.Gun slaving precision detecting system of double-theodolite[J].Ordnance Industry Automation,2011,30(7):73-75.(in Chinese)
[7]孙泽林,王昭,翟唤春,等.双经纬仪交会测量火炮调炮精度的误差分析与抑制[J].光学精密工程,2011,19(10):2434-2441.SUN Zelin,WANG Zhao,ZHAI Huanchun,et al.Analysis and control of error on two theodolite intersection measurement for gun rotated accuracy of artillery[J].Optics and Precision Engineering,2011,19(10):2434-2441.(in Chinese)
[8]张光,任国全,张英堂,等.调炮精度检测中双经纬仪优化布 站 方 法[J].火 力 与 指 挥 控 制,2011,36(9):176-179.ZHANG Guang,REN Guoquan,ZHANG Yingtang,et al.Research on optimizing disposition method of double theodolites in gun rotated precision detection[J].Fire Control &Command Control,2011,36(9):176-179.(in Chinese)
[9]侯宏录,李宏.光电经纬仪测量飞行器三维坐标方法及误差分析[J].光电工程,2002,29(3):4-8.HOU Honglu,LI Hong.Measurement of vehicle three dimension coordinate with photoelectrical theodolite and error analysis[J].Opto-Electronic Engineering,2002,29(3):4-8.(in Chinese)
[10]吴能伟,陈涛.异面交会法在光电经纬仪中的应用[J].仪器仪表学报,2006,27(增刊2):1233-1235.WU Nengwei,CHEN Tao.Application of non-coplane intersection method to photoelectric theodolite[J].Chinese Journal of Scientific Instrument,2006,27(Sup2):1233-1235.(in Chinese)
[11]侯宏录,周德云.光电经纬仪异面交会测量及组网布站优化设计[J].光子学报,2008,37(5):1023-1028.HOU Honglu,ZHOU Deyun.Measurement method and location optimization of multi-photoelectric theodolite for positioning of aviation weapons[J].Acta Photonica Sinica,2008,37(5):1023-1028.(in Chinese)
[12]顾青,毛建民.光电经纬仪空中轨迹交会测量方法研究及误差分析[J].地矿测绘,2009,25(1):12-14.GU Qing,MAO Jianmin.Research on photoelectric theodolite intersection based on air trajectory testing methods and its error[J].Surveying and Mapping of Geology and Mineral Resources,2009,25(1):12-14.(in Chinese)
[13]于来法.无接触电子经纬仪工业测量系统的原理和精度[J].勘察科学技术,1994(4):42-47.YU Laifa.Principle and precision of remote electrontheodolite industrial surveying system[J].Site Investigation Science and Technology,1994(4):42-47.(in Chinese)
[14]张福民,曲兴华,叶声华.基于蒙特卡罗仿真方法的大尺寸测量不确定度分析[J].计算机集成制造系统,2009,15(1):184-187,196.ZHANG Fumin,QU Xinghua,YE Shenghua.Uncertainty analysis in large-scale measurement based on Monte Carlo simulation method[J].Computer Integrated Manufacturing System,2009,15(1):184-187,196.(in Chinese)
