弹道一致性评定中的样本顺次正态性检验
2015-11-27张领科董家强
张领科,董家强
(1.南京理工大学 能源与动力工程学院,江苏 南京 210094;2.中国白城兵器试验中心,吉林 白城 137001)
弹道一致性是指同一火炮武器系统,在气象条件、射击方法等都相同的条件下,发射两类射弹,在弹道上的平均参数差异不大的性质,强调平均弹道参数差异的状况;其评定方法在国军标中采用配对样本的均值t检验,有时也采用独立样本的均值t检验[1]。文献[2]指出,采用均值t检验法的前提是样本服从正态分布。因此,弹道一致性评定中配对样本之差所构成的新样本或独立样本本身的正态性进行检验是必需的。
最经典的正态性检验方法是Lilliefors[3]检验与Shapiro-Wilk[4]检验,且Shapiro-Wilk检验效能优于Lilliefors检验[5]。Epps与Pulley[5]基于经验特征函数提出了一种高效的正态性检验方法(Epps-Pulley检验),随后Henze[6]对Epps-Pulley检验的分布限进行了近似,使得当样本容量n≥10时对统计量的计算相对简单,并给出了4≤n≤9时不同置信水平下的临界值。Mardia[7]详细阐述了具有较高检验精度的联合Skewness-Kurtosis检验法,主要适用于事先已知样本倾向性分布。Miguel[8]提出了两种基于U 过程的正态性检验方法,采用随机抽样的方法证明了具有相对于Lilliefors检验较高的效能。王斌会[9]等人重点研究了QQ 图法、PP 图法与SP 图法的检验效能,指出在小样本(n=20)时,SP 图法效能最优,大样本量(n>50)时,3种方法效能基本一致。大量的研究结果表 明,Shapiro-Wilk 检 验 与Epps-Pulley 检 验 具有较高的检验效能,并已列入了ISO 5479-2002正态性检验标准,我国也推荐采用ISO 标准,但标准规定仅适用于样本容量n≥8的情形,未给出n<8时的接受临界值;并且指出,当样本分布近似为低峰对称分布(||<1/2和β2<3)与非对称分布(||>1/2)时采用Shapiro-Wilk检验,其他宜选用Epps-Pulley 检 验[10],并 将Skewness-Kurtosis检验与QQ 图法作为补充。
笔者通过比较分析Shapiro-Wilk检验与Epps-Pulley检验的效能,基于弹道一致性评定的特点,提出弹道一致性评定中样本正态性检验的顺次检验方法,指导工程应用。
1 两种弹道一致性评定方法
弹道一致性评定通常采用分组多发试验方法,用弹量为m×n发,m为组数,n为每组发数,根据口径差异并考虑到节约试验费用,国军标规定试验用弹量情况:若d<57mm时,为3×10发;若57mm≤d≤160mm 时,为3×7发;若d>160mm 时,为3×5发。由此可见,弹道一致性评定中的样本正态性检验主要是单组小样本(n≤10)和多组(m=3)的检验。
假设(1)为检验弹,(2)为被检验弹;两弹交叉对比射击m×n发;获得标准化的地面或立靶射击的弹丸落点纵向坐标X、高低坐标Y、横向坐标Z和飞行时间T的试验数据。弹道一致性评定就是对两种弹的上述参数是否存在显著差异进行检验。
1.1 配对样本评定模型
为了减少试验条件变化对试验弹与被试弹所造成系统误差的影响,两种弹配对交叉射击,检验模型如式(1)所示,以Y为例。

式中:tα/2[m(n-1)]为置信度α下自由度f=m(n-1)时的临界值;EΔy为m组综合中间误差。各参量计算见文献[1]。判别准则为:若||≤λ′αEΔy,认为两弹满足弹道一致性;若||>λ′αEΔy,认为两弹不满足弹道一致性。
1.2 独立样本评定模型
弹道一致性试验中由诸元误差、弹道误差、气象误差及技术准备误差等随机误差对两弹产生的影响是相同的,经标准化处理后的两弹95%试验数据之间具有较强的独立性,故可采用独立样本评定模型[11],如式(2)所示,同样以Y为例。

式中:λ″α为弹道一致性界限系数,λ″α=0.674 5×自由度f=2m(n-1);其他参数含义见文献[1]。判别准则为:若||≤λ″αEy,认为两弹满足弹道一致性;若||>λ″αEy,认为两弹不满足弹道一致性。
1.3 评定模型比较分析
配对样本与独立样本均值t检验模型在工程中有着广泛的用途。文献[12]指出,两种方法的选择主要依据相关系数r的符号,当r>0时,配对检验效能优于独立检验效能;当r<0时,独立检验效能优于配对检验效能;特别当r≈1.0时,优选配对检验模型。由配对评定模型可以看出,它由单组配对样本均值t检验的变化形式,应用于多组检验,尽管该模型不要求两弹弹道一致性试验样本是否服从正态分布,但样本差构成的多组新样本是应服从正态分布。对于独立检验模型,则要求两弹弹道一致性试验样本自身服从正态分布。如前述,尽管采用交叉配对射击试验方法,但所得到的两弹自身试验数据具有较强的独立性,故两种方法在很多情况都是适用的。总而言之,对于弹道一致性评定,配对检验模型效能优于独立检验模型。因此,利用上述评定模型前需对样本正态性检验,鉴于弹道一致性评定的小样本与多组特点,比较Shapiro-Wilk 与Epps-Pulley检验效能,并给出适用于小子样情况下的顺次正态性检验方法。
2 两种正态性检验方法
对正态性检验已发展了很多检验方法,推荐使用国标GB/T 4882-2001给出的两种具有较高检验效能且适用性较好的正态性检验方法。
2.1 Shapiro-Wilk检验
正态性假设检验:
H0:总体服从正态分布。
H1:总体不服从正态分布。
2.1.1 单组情况
1)对n个样本排序:x(1)≤x(2)≤… ≤x(n)。
2)计算检验统计量W。
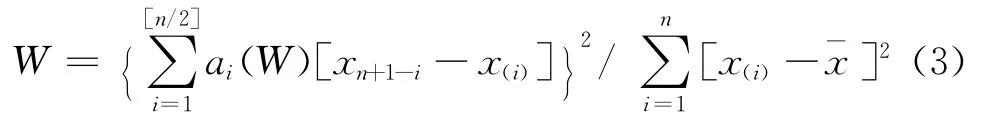
式中:为样本均值;ai(W)为计算所需的系数;[n/2]为n/2的整数部分。
3)将x(1),x(2),…,x(n)的值代入上式计算统计量W的值,根据给定的置信水平α和样本容量确定统计量W的α分位数Wα。
4)作出判断:若W<Wα,拒绝零假设;若W≥Wα,则接受零假设。
2.1.2 多组情况
针对弹道一致性试验的分组情况,为了多组正态性检验,这里补充完善了文献[1]中分组情况下W检验(n≥3)。
1)设每组样本观测值Wi(i=1,…,m)。
2)计算Zi。
Zi=v(n)+η(n)(Wi-L(n))/(1-Wi)
式中v(n)、η(n)、L(n)可用多项式y=B0+B1x+B2x2+B3x3+B4x4+B5x5+B6x6+B7x7+B8x8+B9x9拟合,多项式系数如表1所示,适用于n≥3的情况。

表1 参数多项式拟合系数
4)确定自由度为2m的χ2分布的1-α分位数(2m)。
5)作出判断:如果χ2>(2m),则有理由认为m组均来自正态分布,否则,拒绝正态分布的假设。
2.2 Epps-Pulley检验
Epps-Pulley检验是基于经验特征函数的一个无方向正态性检验方法,它对多种被择假设都有较高的功效,对于弹道一致性评定中的正态性检验仅适用于单组检验,检验统计量为


检验步骤:
1)当 样 本 容 量n≤9 时,按 式(4)计 算Epps-Pulley检验统计量WEP,并根据显著水平α与n确定临界值cα,如表2所示。表中数据采用蒙特卡洛法随机模拟1 000万次产生,而文献[6]为20万次,故本文给出的相对更精确。

表2 临界值cα 的确定
2)作出判断:若WEP>cα,则拒绝零假设,认为不服从正态分布;否则,接受零假设。
3)当样本容量n≥10时,由WEP计算修正统计量W*EP与转换变量Zn。

式中:γ=3.552 95;δ=1.230 62;ξ=0.020 682;λ=2.266 4。
4)作出判断:当Zn>Z1-α时,认为样本不服从正态分布,Z1-α为标准正态分布1-α分位点数。
3 两种检验方法效能分析
为了比较Shapiro-Wilk检验与Epps-Pulley检验的检验效能(存伪概率),选取7 种典型的分布,Beta分布(3种)、指数分布、对数正态分布、Gamma分布(2种)、学生氏t分布、均匀分布和瑞利分布。采用蒙特卡洛随机抽样的方法,分别对两种检验的效能进行计算,如表3所示。表中括号外数据为Shapiro-wilk检验效能,括号内为Epps-Pulley检验效能。

表3 两种方法检验效能比较%
由表3中的计算存伪概率可以发现,通过调节Beta分布的两个参数,可以模拟对称分布与不对称的情况;指数分布具有很强的不对称特性;对数正态分布与正态分布差异性最大;Gamma分布也可模拟强不对称性;t分布、瑞利分布和正态分布较为近似;均匀分布在小子样情况下也呈现较强的正态性。除此之外,在小子样情况(n≤30)Shapiro-Wilk检验与Epps-Pulley 检验的检验效能相当,Shapiro-Wilk检验略优于Epps-Pulley 检验,这与文献[5]的结论一致。
4 顺次正态性检验
4.1 检验思想
考虑弹道一致性试验中试验数据本身存在次序性,因此,在正态性检验中采用次序正态性检验从而推断整组正态性是可行的。具体方法:
1)单组检验:采用Shapiro-Wilk检验或Epps-Pulley检验方法,依次分别对3,4,5,…,n法进行正态性检验,若80%均判定为正态分布,则认为样本来自正态总体;否则,拒绝正态性结论。
2)多组检验:采用多组Shapiro-Wilk 检验方法分布对m组单独检验,若有理由认为整体m组服从正态分布,则优先认为单组也服从正态分布(对于单组不服从正态分布的分析引起的原因,最好两方面统一)。
4.2 算例分析
某被检验弹弹道一致性立靶参数T、Y与Z的试验数据如表4所示。

表4 某弹道一致性试验数据
在给定显著水平α=0.05下检验数据正态性,分别采用Shapiro-Wilk与Epps-Pulley检验方法顺次正态性检验结果如表5所示。
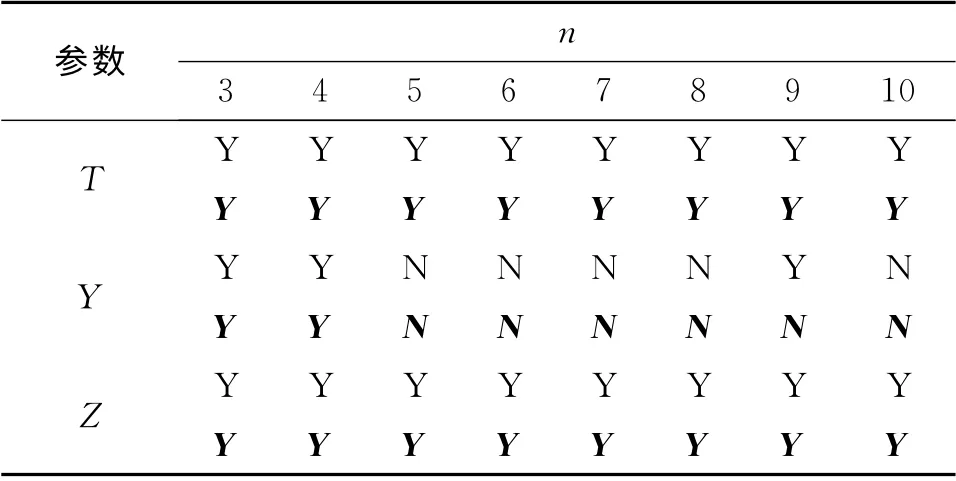
表5 顺次正态性检验结果
由表5可以看出,对于参数Y,Shapiro-Wilk检验接受的只有3个,Epps-Pulley检验接受的只有2个,故可以判定不服从正态分布;而对于参数T与Z,两种检验方法都给出了全部接受,故可以判定服从正态分布。采用样本顺次正态性检验的好处可提高弹道一致性正态性检验结果的可靠性。
5 结论
笔者针对弹道一致性评定中的小子样与多组检验特性,采用蒙特卡洛法计算分析了Shapiro-Wilk 检 验 与Epps-Pulley 检 验 的 效 能,完 善 了Epps-Pulley检验的零假设接受限,提出了一种基于顺次正态性的检验方法,优点是对样本数据分布了解更全面,便于弹道一致性评定前数据正态性来源可靠性的分析,研究结果具有一定的应用价值。
(References)
[1]王中原,张领科.弹箭通用射表及弹道一致性检验方法[M].北京:科学出版社,2008.WANG Zhongyuan,ZHANG Lingke.The test method of using the same firing table and trajectory consistency[M].Beijing:Science Press,2008.(in Chinese)
[2]全国统计方法应用标准化技术委员会.GB/T 4882-2001 数据的统计处理和解释:正态性检验[S].北京:中国标准出版社.2001:9.National Statistical Method Standardization Technical Committee.GB/T 4882-2001Statistical interpretation of data:normality tests[S].Beijing:China Standard Publishing House.2001:9.(in Chinese)
[3]SHAPIRO S S,FRANCIA R S.An approximate analysis of variance test for normality[J].Journal of the American Statistical Association,1972,67:215-216.
[4]SHAPIRO S S,WILK M B.An analysis of variance test for naomality[J].Biometrika,1965,52:591-611.
[5]EPPS T W,PULLEY L B.A test for normality based on the empirical characteristic function[J].Biometrika,1983,70:723-726.
[6]HENZE N.An approximation to the limit distribution of the Epps-Pulley test statistic for normality[J].Metrika,1990,37:7-18.
[7]MARDIA K.Handbook of statistics-tests of univariate and multivariate normality[M].North-Holland:Krishnaiah,P.R.,1980.
[8]MIGUEL A A,WANG Y S.Some new tests for normality based on U-processes[J].Statistics &Probability Letters,2006,76:69-82.
[9]王斌会,徐勇勇.正态性检验的图示方法及其应用[J].数理统计与应用概率,1996,11(3):249-256.WANG Binhui,XU Yongyong.Graphic method and application of normality test[J].Mathematical Statistics and Applied Probability,1996,11(3):249-256.(in Chinese)
[10]梁小筠.我国正在制订“正态性检验”的新标准[J].应用概率统计,2002,18(3):269-276.LIANG Xiaoyun.A new national standard on normality tests is being worked out[J].Chinese Journal of Applied Probability and Statisties,2002,18(3):269-276.(in Chinese)
[11]张领科,王中原.稳健独立样本均值检验界定弹道一致性 分 析[J].弹 箭 与 制 导 学 报,2005,25(2):377-379.ZHANG Lingke,WANG Zhongyuan.The analysis of stable mean testing defining trajectory consistency[J].Journal of Projectiles,Rockets,Missiles and Guidance,2005,25(2):377-379.(in Chinese)
[12]董秀玥.配对t检验与成组t检验优选方法研究[J].数理医药学杂志,2010,23(1):11-14.DONG Xiuyue.The better choice study of pairedttest and groupttest[J].Journal of Mathematical Medicine,2010,23(1):11-14.(in Chinese)
