基于小波尺度谱重排与小波排列熵的自动机故障诊断
2015-11-27潘宏侠马百雪
潘宏侠,马百雪,许 昕
(中北大学 机械与动力工程学院,山西 太原 030051)
自行火炮作为炮兵现代化的重要标志、现代炮兵的重要组成部分,于上世纪五十年代已经在我国装甲兵部队中广泛使用,并且逐渐发展为拥有不同体系和用途的武器装备系列。高速自动机作为小口径火炮的核心部件,受高温、高压、工作环境恶劣的影响,部件产生磨损、裂纹在所难免,因此必须对自动机进行可靠性监测与故障诊断。
自动机获得的振动信号往往具有大量的背景噪声,属于非平稳、短时瞬态信号,而且一些构件的裂纹及磨损的振动响应也很微弱[1-2]。而小波包变换通过伸缩和平移运算实现对信号的多尺度细化分析,可以在时频域内表示信号的局部特征,能有效地提取信号的时频特征量。小波变换的尺度谱被认为是拥有一个相对恒定带宽的频谱,是对信号时频信息的反映。小波尺度谱重排是对小波尺度谱的一种再分配方法,具有更好的时频集中性和较少的干扰项,提高了信号时频分布的可读性,且能很好地表现信号中能量较小的微弱信号,利于提取早期故障特征,可以进行信号的时频特征提取、消噪处理[3]。
笔者将小波尺度谱重排应用于自动机故障信号的早期预处理,并结合同样对信号微弱变化特征敏感的排列熵算法作为预处理信号所要提取的特征量进行故障诊断。诊断结果表明该方法可以对自动机故障进行有效的诊断。
1 小波尺度谱重排基本原理
对所有的信号x(t)、ψ(t)∈L2(R),x(t)作连续小波逆变换:
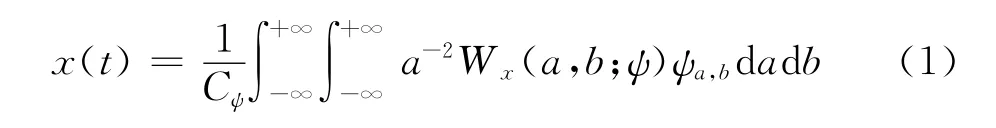
由逆变换可知,信号x(t)的连续小波变换能量是守恒的,没有任何损失,因此下式(2)是成立的:

设Gsx(a,b;ψ)=|Wx(a,b;ψ)|2,为小波尺度谱。若ω0为ψ(t)的中心角频率,则Gsx(a,b;ψ)表示某一区域的能量密度的均值,该区域是在时频面上以(ω0/ai,aitc+bi)为几何中心,但该区域的能量并非几何对称。如果把平均值分配到几何中心点并不合理,只有分配到局域能量的重心才能代表此局域的能量分布。小波尺度谱重分配就能实现这个目的,它能提高信号的时频聚集性,减少干扰。

式中b′(a,b)和a′(a,b)可由下式求得:

2 排列熵理论
2.1 排列熵算法
Christoph Bandt等人提出的排列熵(Permutation Entropy,PE)的概念,这是一种平均熵参数,用途是衡量一维时间序列复杂度。
排列熵算法的基本原理参考文献[4]。排列熵的计算流程图如图1所示。

2.2 小波包排列熵
根据小波排列熵的计算方法,对小波包排列熵特征值[5-6]的提取步骤如下:
1)小波包变换。对振动信号进行小波包分解,这里使用db1小波基对信号进行3层分解,得到各层的小波系数,分别包含从低频到高频的不同频带的信息。
2)小波系数重构。对第3层小波系数进行重构,得到重构分量Sj={sj(k),k=1,2,…,N;j=1,2,…,8},N为原始信号的长度。
3)小波重构信号预处理。对第3层小波重构系数分别进行小波尺度谱重排进行预处理。
4)分别计算得到排列熵。通过计算,选取最佳嵌入维数和最佳延迟时间对预处理后的小波系数进行相空间重构,通过计算得到各分量的排列熵。
3 应用实例
3.1 自动机故障方案设计
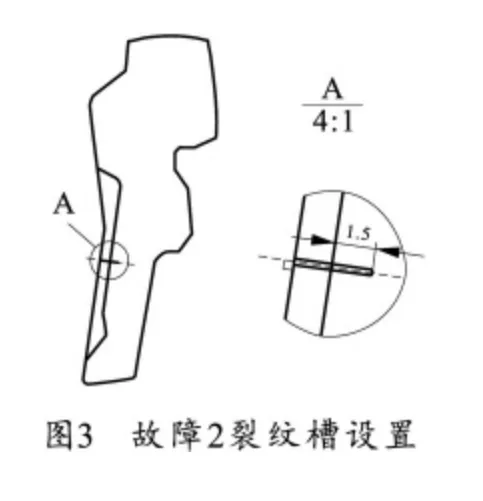
根据靶场工作人员的经验和受力分析,本次试验采用电火花线切割的方法在自动机闭锁片、枪击框上预制裂纹槽,使裂纹在射击过程中自动的产生和扩展来产生裂纹、设置故障[7-8]。模拟了闭锁片裂纹、机头故障,在左右闭锁片上对称地设置了两种裂纹故障(故障1和2),在机头左右两侧的圆角矩形窗后端的两对圆角上(即闭锁片旋转时与机头接触部位)设置裂纹故障(故障3)。故障1和故障2设置如图2、3 所示。试验采样频率设置为204.8kHz。

3.2 基于小波尺度谱重分配的自动机振动信号预处理
本次试验分4种工况(分别对应正常、故障1、故障2和故障3),进行了单发射击3次、三连发射击3次和五连发射击2次共3种状态,每种状态的响应数据一致性较好,每种工况发射枪弹22发,总计有效试验数据8×4组。以下以单发正常工况为例进行说明。由于自动机的各机构是顺时针依次进入和退出工作,再加上冲击响应信号的衰减很快,所以前一机构由于撞击而产生的振动响应信号,对后一机构工作期间产生的振动信号没有影响或影响很小,所以只截取了振动信号上作用于闭锁片时间段(即开锁、闭锁、后坐阶段)的某段信号进行分析。图4为正常单发x轴方向振动信号,图5为自动机在正常工况下单发x向采集的振动信号分段截取后组合信号。

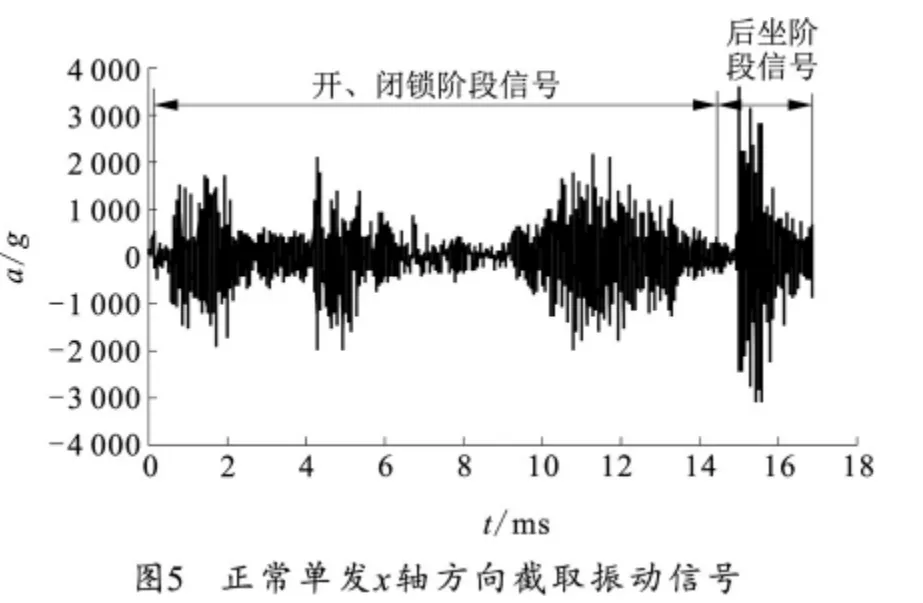
笔者选用复Morlet小波作为小波变换的小波基对振动信号进行时频变换,得到小波尺度谱,如图6所示,可见振动信号的尺度谱分布杂乱,冲击特性并不明显。
对振动信号小波尺度谱进行重分配后结果如图7所示。发现分配后的尺度谱比较集中,冲击特性比较明显,实现了自动机振动信号小波变换时频分析的早期预处理,可见自动机的振动信号主要集中在采样点数为2 500~4 000之间,为后期时频分析提供信息。


3.3 基于小波包排列熵的自动机特征向量提取
选取嵌入维数m=4,延迟时间τ=1对尺度谱重排后的小波包系数进行相空间重构,通过计算得到各分量的排列熵。
单发情况下4 种工况自动机振动信号的排列熵如表1所示。

表1 自动机振动信号小波包排列熵
通过表1可以发现,不同工况的振动信号的小波包排列熵有着明显的差异,设正常、故障1、故障2、故障3 的小波包排列熵分别表示为δPE1,δPE2,δPE3,δPE4。δPE1>δPE3>δPE4>δPE2,说明正常工况的排列熵值最大,其次是故障2,故障3,故障1最小。说明正常工况的振动信号随机性最大,而其他3种工况的随机性相对较小,比较规则。可以作为后续故障识别的特征向量。
3.4 基于小波包排列熵的自动机故障分类
取小波包排列熵作为分类的特征向量,共包括故障1、故障2、故障3和正常4种工况,原始信号为单发x轴向振动信号。每种工况包含8个特征值,这里每组工况取前4 个为训练集,后4 个为测试集,使用经过网格搜索法优化参数的SVM 对特征量进行分类识别。分类结果如图8所示。

由图8可以看出,经优化参数的SVM 分类识别,其正确率是87.5%(即14/16)。
4 结论
根据自动机运动过程及振动信号进行时频域分析,截取与闭锁运动相关信号进行小波包变换,运用小波多尺度重排方法对各层小波包系数进行小波尺度重排,提取了小波包排列熵作为自动机故障特征量。
运用网格搜索法对SVM 核心参数优化,运用优化后的SVM 方法进行故障模式识别,经建模、训练测试,准确地识别出了自动机的故障类型,正确率接近90%,说明使用小波尺度谱重分配与小波排列熵可以进行自动机故障诊断,证明了该方法的有效性。
(References)
[1]胡家顺,冯新,李昕,等.裂纹梁振动分析和裂纹识别方法研究进展[J].振动与冲击,2007,26(11):146-152.HU Jiashun,FENG Xin,LI Xin,et al.State-of-art of vibration analysis and crack identification of cracked beams[J].Journal of Vibration and Shock,2007,26(11):146-152.(in Chinese)
[2]LEI Yaguo,HE Zhengjia,ZI Yanyang.A new approach to intelligent fault diagnosis of rotating machinery[J].Expert Systems with applications,2008,35:1593-1600.
[3]廖传军,李学军,刘德顺.小波再分配尺度谱在声发射信号特征提取中的应用[J].机械工程学报,2009,45(2):273-279.LIAO Chuanjun,LI Xuejun,LIU Deshun.Application of reassigned wavelet scalogram in feature extraction based on acoustic emission signal[J].Journal of Mechanical Engineering,2009,45(2):273-279.(in Chinese)
[4]冯辅周,司爱威,饶国强,等.基于小波相关排列熵的轴承早期故障诊断技术[J].机械工程学报,2012,48(13):73-79.FENG Fuzhou,SI Aiwei,RAO Guoqiang,et al.Early fault diagnosis technology for bearing based on wavelet correlation permutation entropy[J].Journal of Mechanical Engineering,2012,48(13):73-79.(in Chinese)
[5]郑近德,程军圣,杨宇.多尺度排列熵及其在滚动轴承故障诊断中的应用[J].中国机械工程,2013,24(19):2641-2646.ZHENG Jinde,CHENG Junsheng,YANG Yu.Multiscale permutation entropy and its applications to rolling bearing fault diagnosis[J].China Mechanical Engineering,2013,24(19):2641-2646.(in Chinese)
[6]BOZHOKIN S V,SUSLOVA I B.Wavelet-based analysis of spectral rearrangements of EEG patterns and of non-stationary correlations[J].Physica A:Statistical Mechanics and its Applications,2015,421:151-160.
[7]赵勇,杨慎华,郑祺峰,等.激光预制裂纹槽的断裂分析[J].吉林大学学报:工学版,2011,41(4):984-987.ZHAO Yong,YANG Shenhua,ZHENG Qifeng,et al.Fracture analysis of specimen with crack notch processed by laser[J].Journal of Jilin University:Engineering and Technology Edition,2011,41(4):984-987.(in Chinese)
[8]潘宏侠,兰海龙,任海锋.基于局域波降噪和双谱分析的自动机故障诊断研究[J].兵工学报,2014,35(7):1077-1082.PAN Hongxia,LAN Hailong,REN Haifeng.Fault diagnosis for automata based on local wave noise reduction and bispectral analysis[J].Acta Armamentarii,2014,35(7):1077-1082.(in Chinese)
