倒双谱的分形维数在故障诊断中的应用

吴文兵，叶福兰，陈章斌

(福州外语外贸学院，福建福州350018)

0 前言

高阶谱由高阶累积量进行多次傅里叶变换得来。高阶累积量可以消除高斯噪声，因而可以提取复杂信号中的非高斯信号。与功率谱相比，高阶谱同时含有信号的幅度信息和相位信息。高阶累积量可以检测和描述系统的非线性，因而常用于机械系统非线性振动信号的研究［1-2］。高阶谱估计主要有以下几个方面的应用:声纳与雷达处理、多维信号处理、非线性系统分析、生物医学信号处理、谐波恢复、信号检测、陈列处理等。由于机械振动信号的非线性、非高斯性和环境中噪声的高斯性，因而高阶谱方法可以去除振动信号中的高斯噪声，保留其中的非高斯信息，为故障处理提供有力的分析方法。倒谱分析也是机械故障诊断的有效方法，倒谱是将对数功率谱进行反傅立叶变换后得到的，它可以进一步将信道特性和激励特性有效地分开，但噪声对倒谱分析的结果具有较大的影响［3-4］。机械设备故障诊断是通过测量机械设备工作状态的特征信号来识别其状态的。由于实际测量获得的信号的切片谱在一定的尺度上具有分形特征，即这些信号切片谱的分形维数会随着系统状态的改变而变化，因此分形维数能在一定程度上反映机械设备的运行状态［5-7］。提取分形维数这一特征量，将有助于对机械设备的正常工作状态和故障状态进行诊断和识别。

本文作者将倒谱分析、双谱分析以及分形理论相结合，针对溢流阀故障信号具有的机械振动信号非线性等共性，提出了通过计算倒双谱的分形维数进行故障检测和诊断的方法，并应用到溢流阀的故障诊断中。

1 倒谱与倒双谱

设{x(n)}为零均值k阶平稳随机过程，功率谱定义为:

双谱定义为:

设ω1＝ω2＝ω时，即得到AR双谱的对角切片Bx(ω，ω)，其中 c3x(τ1，τ2)为三阶累积量:

功率谱对数值的逆傅里叶变换称为倒谱。设信号x(n)的功率谱为Sx(ω)，则倒谱Cx(τ)为

将Bx(ω，ω)代入上式，代替Sx(ω)，即得到倒双谱。

实际计算中倒双谱采用下式:

2 容量维与关联维

按照文献 ［5］，即采用盒子覆盖算法来计算功率谱的容量维数。对于Dc维物体:

N(r)∝(1/r)Dc→lim N(r)＝(1/r)Dc

取对数得容量相似维数:

式中:L为线段长度，r为尺子长度，L与r之比为N。

按照文献［7］，关联维数可以由实测一维时间序列，利用基于相空间重构的G-P算法直接计算得到。

基于相空间重构，考察m维相空间中的一对相点

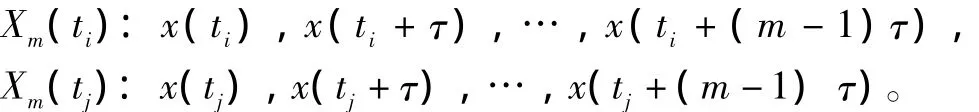
设其距离为εij(m)，则有

式中:‖·‖为范数，则关联积分为:

式中:Nm＝n-(m-1)τ为相点数，ε为m维超球半径 (标度)，θ是Heaviside阶跃函数，即有

适当选取标度ε，在无标度区内有:

则D2(m)即为关联维数。

3 数据采集

溢流阀在每个液压系统中几乎都要用到，其性能的好坏对整个系统的正常工作有很大影响。它可作为安全阀、卸荷阀和加载阀等使用，也可与远程调压阀组合以实现远距离调压等。图1中，先导型溢流阀在液压回路中用作安全阀，防止液压系统过载。正常工作情况下，系统压力不超过溢流阀的调定压力时，溢流阀关闭不起溢流作用。当系统压力达到溢流阀的调定压力值时，溢流阀打开，将油液溢回油箱，使压力不再上升，以保证系统的安全。文中进行的实验人为设置了在主阀芯的阻尼孔处穿上一根细导线的故障。

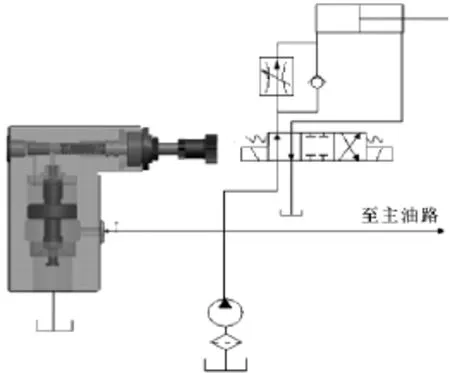
图1 溢流阀工作回路

实验分别在溢流阀正常工作状态和故障状态各自采集了10组和11组共21组数据。实验使用的数据个数为512个。

4 谱图

为了进行故障识别，将实验中测得的正常状态和故障状态的21组数据分别求出其双谱对角切片和倒双谱。在正常状态和故障状态下，在3种不同的油压下 (1 MPa、2 MPa、4 MPa)，将两种状态的双谱对角切片和倒双谱各选取1组示于图2—5。其中图2、3的x轴表示频率，单位为Hz，y轴表示归一化后的幅值大小，无量纲。由图4、5的x轴表示数据，单位为个，y轴与图2、3相同，也表示归一化后的幅值大小，无量纲。可以看出，在倒谱方式下，从图像峰值的构成和数量来看，2种状态的区分较为明显。

图2 正常状态双谱对角切片图

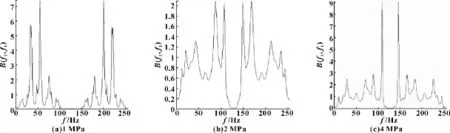
图3 故障状态双谱对角切片图

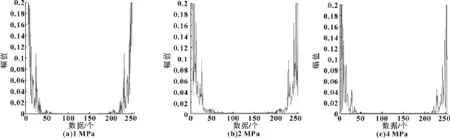
图4 正常状态倒双谱图

图5 故障状态倒双谱图

5 实验结果与分析

为了有效判别故障，分别利用双谱对角切片和倒双谱作为工具，鉴于双谱对角切片的光滑性和倒双谱的时序性，分别计算了信号在正常状态和故障状态下双谱对角切片的容量维以及倒双谱的关联维。正常状态以及故障状态倒双谱的关联维数值示于表1。为了在直观上有效区分故障诊断结果，通过EXCEL软件绘制了倒双谱关联维数值的点折线图，见图6。图6的横坐标代表数据，单位为组，纵坐标表示计算出的关联维数值，无量纲。从图6中可以看出，在倒谱方式下，正常状态和故障状态下信号的关联维数在整体上区别较为明显，为了准确统计诊断正确率，特选定故障状态第1组数据的关联维数值作为分界值，即以关联维数值大于等于0.456 2确定为故障状态，以小于0.456 2确定为正常状态，则正常状态和故障状态误判的数据个数分别是2个和1个，总体正确率为3/21＝1/7，超过了85%，这一结果在故障诊断中算是良好的。文中同时对相同信号的双谱对角切片的容量维进行了计算，结果如图7。图7的横坐标代表数据，单位为组，纵坐标表示计算出的容量维数值，无量纲。从图中可以看出，两种状态难以区分。为了进行对比，还对信号的倒谱计算了关联维以及信号的功率谱计算了容量维，信号的倒谱和功率谱分别在正常状态和故障状态下选取一组，如图8—11所示。图8、9的坐标意义与图4、5相同，图10、11的坐标意义则与图2、3相同。倒谱关联维和功率谱容量维的计算结果见图12和图13，图12和图13的坐标意义分别与图6、7相同。图12和图13所表示的2种状态均难以区分。

表1 正常状态和故障状态倒双谱的关联维数值

图6 正常状态和故障状态倒双谱关联维折线图

图7 正常状态和故障状态双谱对角切片容量维折线图

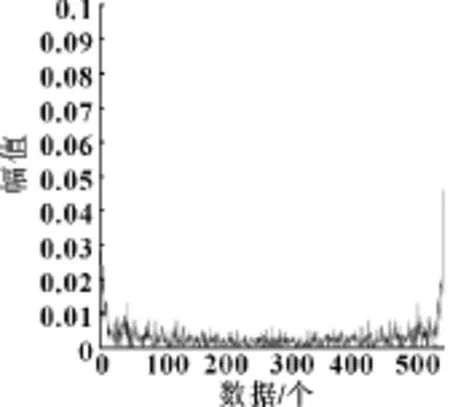
图8 正常状态倒谱

图9 故障状态倒谱

图10 正常状态功率谱

图11 故障状态功率谱

图12 正常状态和故障状态倒谱关联维折线图

图13 正常状态和故障状态功率谱容量维折线图

文中在所选用实验数据的基础上，通过对比功率谱、倒谱、双谱对角切片以及倒双谱的故障诊断效果，得出了倒双谱能取得最佳诊断效果的结果。由于双谱可以从采集信号中最大限度地剔除掉噪声的干扰，从而有效提取信号中的信息。这说明双谱具有很强的消噪能力，理论上可以抑制高斯噪声。对信号进行分析得出它的倒谱参数的过程称为同态处理，倒谱参数所包含的信息也比其他参数多，同时受信号传递路径的影响较小，但噪声对倒谱分析的结果具有较大的影响。倒双谱则将两者的优点很好地结合了起来。由于分形维数能在直观上度量不规则图形的粗糙度，因而振动信号倒双谱的分形维数可以在一定程度上反映机械设备在不同运行期间运行性质的变化，可以直接反映该设备在此期间的运行状况。因此，文中的实验数据在通过功率谱、倒谱以及双谱对角切片都未能取得理想效果时，通过计算倒双谱的分形维数而取得了良好的故障诊断效果是完全可以从理论上得到合理解释的。

6 结论

通过计算倒双谱的分形维数而取得了良好的故障诊断效果，说明在现有理论的基础上，通过将各种方法的优点相结合的方式来提高机械故障诊断正确率的方式是可行的。

［1］KOCUR Dusan，STANKO Radoslav.Order Bispectrum:A New Tool for Reciprocated Machine Condition Monitoring［J］.Mechanical Systems and Signal Processing，2000，14(6):87l-890.

［2］蒋雨燕，黄宜坚.时间序列双谱在调速阀故障诊断中的应用［J］.集美大学学报，2008，13(2):175-179.

［3］李辉，郑海起，唐力伟.基于倒阶次谱分析的齿轮故障诊断研究［J］.振动与冲击，2006，25(5):65-68.

［4］李辉，郑海起，唐力伟.基于倒双谱分析的轴承故障诊断研究［J］.振动、测试与诊断，2010，30(4):353-356.

［5］吴文兵，黄宜坚，陈文芗.基于机械故障诊断的高阶谱耦合性能分析［J］.振动、测试与诊断，2012，32(1):130-134.

［6］王春来，吴爱祥，刘晓辉.深井开采微震活动容量维Df变化特征［J］.北京科技大学学报，2010，32(11):1379-1382.

［7］张燕平，黄树红，高伟.关联维数在汽轮机故障诊断中的应用［J］.华中科技大学学报:自然科学版，2007，35(7):93-95.