基于双谱特征融合的通信辐射源识别算法

桂云川，杨俊安，万 俊

(1.解放军电子工程学院，安徽 合肥 230037;2.安徽省电子制约技术重点实验室，安徽 合肥 230037)



基于双谱特征融合的通信辐射源识别算法

桂云川1,2，杨俊安1,2，万 俊1

(1.解放军电子工程学院，安徽 合肥 230037;2.安徽省电子制约技术重点实验室，安徽 合肥 230037)

针对当前通信辐射源个体识别方法存在识别效率不高，内在细微特征难以提取等问题，提出了基于双谱特征融合的通信辐射源特征提取算法。该算法通过融合对角积分双谱与双谱对角切片特征组成特征向量，并对对角切片特征提取方法进行了改进，将原信号先进行经验模态分解(EMD)，在得到的本征模函数(IMF)基础上提取对角切片特征，最后使用支持向量机(SVM)得到分类结果。分类实验结果表明，基于双谱特征融合的算法较积分双谱的算法在识别效果上有一定程度的提升。

通信辐射源；特征提取；对角积分双谱；双谱切片

0 引言

在通信对抗领域中，通信辐射源个体识别既是一个研究热点也是一个研究难点，识别出通信目标具体是什么对于通信侦查和通信对抗具有重大意义。通信辐射源识别本质上是一个模式识别的问题，它包括信号的预处理、特征提取、特征选择及分类决策四个模块[1]，特征提取通过对原始数据进行变换得到最能反映类间本质的特征，特征提取的好坏也直接影响了分类的效果。由于电台信号的技术参数差异较小，必须要提取细微的参数才能作为指纹特征对电台进行有效的识别。

实际通信信号经过编码与调制后都呈现出非平稳、非线性与非高斯特性，传统的功率谱与低阶特性分析已经难以揭示信号本质。高阶谱分析广泛地用于信号处理[2]、语音处理[3]及医学诊断[4]等方面，它可以在理论上完全抑制任何高斯噪声和对称分布的非高斯噪声，能够保留信号的幅度和相位信息并且与时间无关，因此高阶谱分析也就成为了目前主流的特征提取方法。三阶谱被称为双谱，是最简单的高阶谱，由于处理方法较为简便，理论方法较为成熟，得到了广泛的应用。

由于直接运用双谱要求计算复杂的二维模板，运算效率不高，导致分类器难以进行有效识别。对此研究人员设法通过积分双谱的算法将二维函数转化成一维函数来解决这一问题。积分双谱的方法按照不同的积分路线选择可以分为径向积分双谱(RIB)、轴向积分双谱(AIB)、圆周积分双谱(CIB)和矩形积分双谱(SIB)[5]四种。文献[6]根据双谱的对称空间，针对双谱的有效运算项提出了沿着平行于双谱主次对角线的路径进行积分的对角积分双谱，降低了无意义运算项对于分类的影响，并验证了算法在低信噪比条件下仍具有较好的效果。双谱的对角切片又称为1.5阶谱，切片内包含了信号的重要特征，并且对角切片的计算简单，可以作为区分辐射源的特征之一。文献[7]通过计算双谱对角切片值，将频域信息拓展到复频域以得到更多的特征信息，但文章采用Chirp-z变换的参数选择对于特征提取好坏有较大影响，并且所提特征含有大量的冗余信息，不利于分类器分类。本文针对上述问题，提出了基于双谱特征融合的通信辐射源识别算法。

1 双谱的基本理论

1.1 双谱的定义

当序列x(t)为零均值复平稳随机过程时，三阶累积量可以定义为：

(1)

式(1)中，x*(t)表示共轭，τ1和τ2代表延迟。双谱又称为三阶累积量谱，是三阶累积量的傅里叶变换，序列x(t)的傅里叶变换为X(ω)，则双谱定义为：

(2)

由定义可以看出，双谱是一个双周期函数，周期大小为2π，即：

B(ω1,ω2)=B(ω1+2π,ω2+2π)

(3)

双谱具有对称性，根据双谱的对称性可以将双谱分为12个扇区，每个扇区包含相同的信息[8]，其对称区间如图1所示。

从图1可以看出，双谱信号是严格按照ω1=ω2对称，ω1=-ω2共轭分布的，并且对角线的两端属于信息无意义项。综合考虑双谱的对称性与周期性，图1的阴影区域包含了双谱所有的有效信息，故在采用积分双谱计算过程中只需要对阴影部分的双谱积分即可，这减少了数据运算量，提高了积分运算的效率。

图1 双谱的对称区间Fig.1 Symmetric interval of double spectrum

1.2 双谱切片

双谱是一个三维立体函数，含有大量的信号内在信息，不利于信号特征的提取，采用复杂的二维模板应用会导致计算量偏大，需要将双谱变成二维函数来分析与提取有用的特征。双谱的谱峰上往往包含有大量的内在特征，双谱的对角切片包含了B(ω1,ω2)内的重要信号特征，通过对双谱的对角切片进行运算，不仅可以有效地提取双谱特征，还可以大量降低算法的复杂度。

对式(2)，令ω=ω1=ω2，得到双谱的主对角切片为：

B(ω,ω)=X(ω)X(ω)X*(2ω)

(4)

图2分别是双谱的截面图、双谱的立体图、以及双谱的对角切片图。

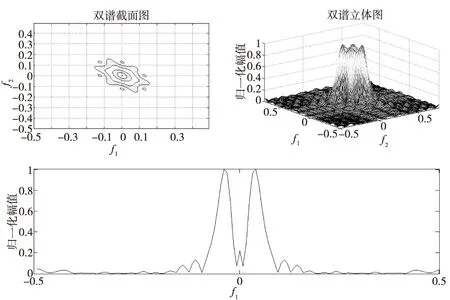
图2 双谱的截面图、立体图及对角切片图Fig.2 The section of the double spectrum, the stereo graph and the diagonal slice

从图2可以看出，双谱的切片图就是沿双谱的立体图按照平面f1=f2所得到的截面，其中f1与f2的长度取决于快速傅里叶变换长度nfft，算法中nfft取128。

2 基于双谱特征融合的特征提取算法

2.1 对角积分双谱

双谱是一个二维数据，通常采用围线积分的方法来避免大量的数据运算。文献[9]和文献[10]分别采用了选择双谱、矩形积分双谱等方法对双谱信息进行了计算，并取得了较好的效果。然而从双谱对称区间分析可以看出，图1中的阴影部分包括了全部双谱信息，并且存在两块相互对称的无意义项，采用矩形积分的方法将会导致信息点取样冗余，不利于特征提取的结果。

相比矩形积分双谱会产生取样冗余问题，对角积分双谱的积分路径沿着平行于主副对角线，针对包含全部双谱信息的区间进行积分计算，避免了对称区间与无意义项的计算，提高了运算效率，其积分表达式为：

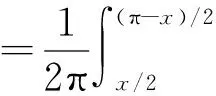
图3表示了对角积分双谱的积分路径，从图上可以看出，对角积分双谱近针对阴影区域的双谱信息进行积分，在保证有效提取了双谱信息的同时大大减小了特征冗余的存在。

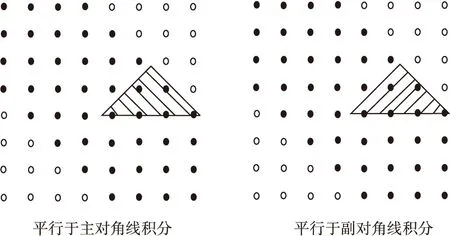
图3 对角积分双谱的积分路线Fig.3 Integral line of diagonal integral double spectrum

2.2 改进的双谱对角切片特征提取算法

2.2.1 经验模态分解算法

1998年，Norden E. Huang等人提出了经验模态分解(EMD)算法[11]，该算法能够自适应地将一个复杂信号分解成一组稳态和线性的本征模函数(IMF)，通过分解将具有不同时间尺度的信号分配到不同阶层的模态中。分解的结果表示为：

其中，ci(t)表示第i阶的分解结果，表示了第i阶IMF分量，rN(t)为最后的剩余信号。IMF反映了原始信号在某种特定意义频段范围内的时域信息，分解后得到的分量更容易反映出信号的细微变换。

2.2.2 双谱切片特征

采用积分双谱的目的是为了解决将二维函数转化成为一维函数的问题，采用双谱的切片同样可以解决这一问题。从图4可以看出，双谱的切片实际上是一条幅频特性曲线，并且由于双谱的对称关系，切片的图形也是严格的对称图形。为了提取切片的幅频特征，反映出谱偏离对称情况，定义一个切片谱对称系数β，令

上式中，切片谱对称系数是对双谱信号的谱偏离对称情况的度量。使用双谱切片的偏离对称系数作为双谱切片的内在特征。此外分形特征也是一种深度刻画信号幅频特性的特征参数，常用的分形特征包括盒维数、信息维数与Lemple-Ziv复杂度。其中盒维数反映了分形集的几何尺度情况；信息维数反映了信号在区域内分布的疏密情况；Lempel-ziv复杂度通过复制和添加两种操作来描述信号序列的特性，并将所需添加的操作次数作为序列的复杂性度量，这些特征在之前的研究中已经被证实是进行个体识别的有效特征。

本文改进的双谱切片特征是建立在EMD分解模型上的特征提取算法，首先将原始信号进行EMD分解，对分解得到的IMF求得双谱切片，并在双谱切片上提取谱对称系数特征及包括盒维数、信息维数与Lemple-Ziv复杂度在内的分形特征。图4是两部电台信号经过EMD分解后各阶IMF双谱切片的示意图(为减少篇幅，只给出了前3阶IMF的双谱切片)。

从图4可以看出，两部电台的双谱切片在结构上存在较大的差异，通过提取IMF双谱切片的细微特征具有可行性。

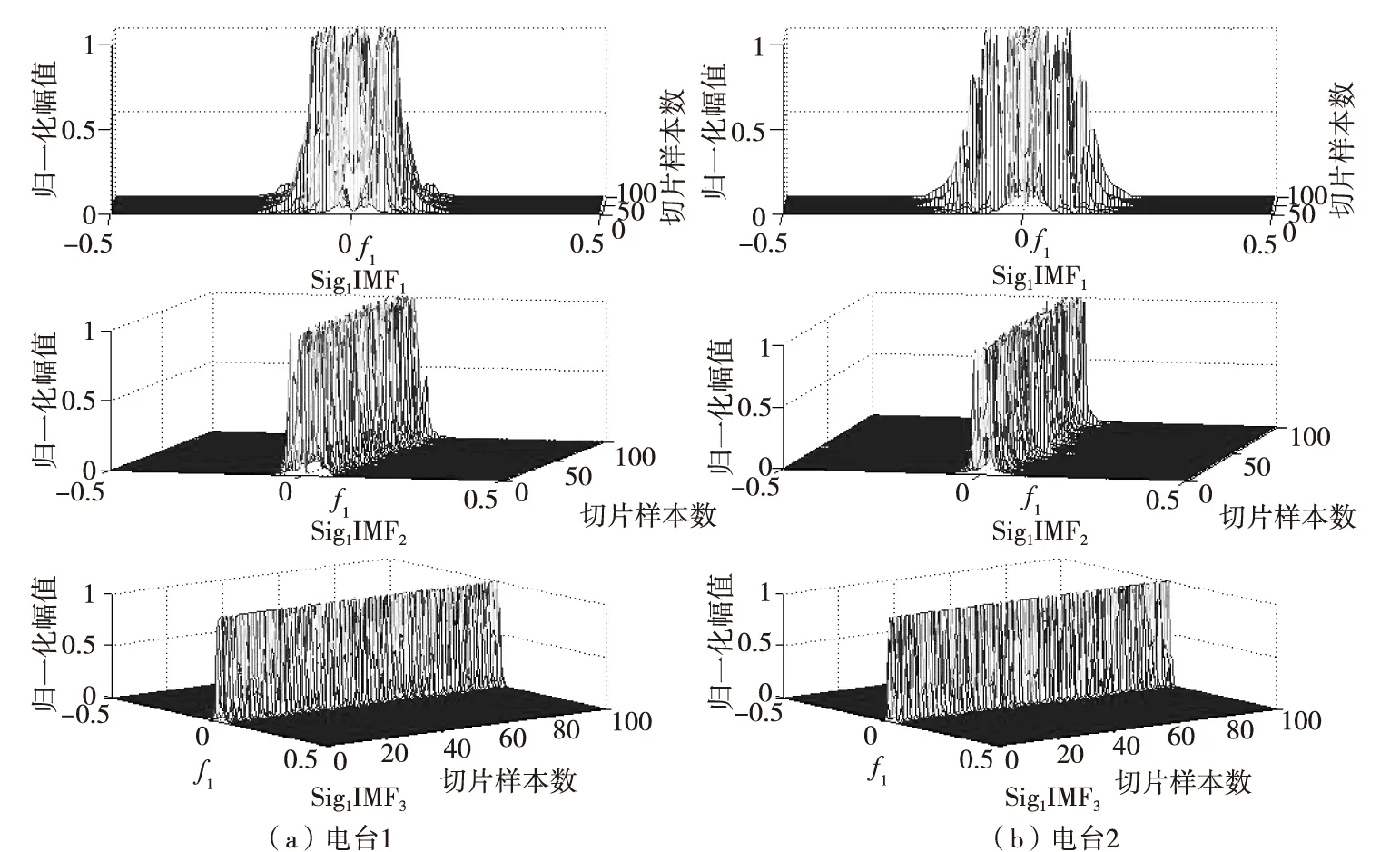
图4 两部电台前3阶IMF对角切片示意图Fig.4 Schematic diagram of the main diagonal slice of the former 3 stage IMFs

3 实验分析

本文的实验数据是6部同型号、同批次的通信电台数据，其实验数据采集背景条件如表1所示。

表1 外场实验数据采集环境

在外场实验数据的实际采集过程中，为方便实验使用，每部电台信号采集两段，两段信号采集间隔内电台经过关机重开，每段信号采集时间大约10 s，其中一段用于训练，另一段用于测试。

在特征提取实验中，将训练信号与测试信号各分为600份。对每份信号进行两方面操作：一方面提取信号的对角积分双谱；另一方面对信号进行EMD分解，求出前5层IMF对应的双谱对角切片，提取切片的谱偏离对称系数、盒维数与Lempel-Ziv复杂度作为切片特征，融合对角积分双谱与对角切片特征组成特征向量。在分类实验中以训练信号中的600份信号作为训练集，随机从测试信号中抽取100份作为测试集，使用基于多项式的SVM分类器进行分类，得到分类结果如表2所示。

为证明本文算法的优势，使用本文提出的基于双谱特征融合的算法对比文献[6]中基于对角积分双谱的算法与本文所提的基于EMD双谱切片特征算法。在分类识别中同样使用基于多项式的SVM分类器进行分类。以识别率作为衡量指标，选择不同信号训练集数量的情况下比较两种算法的识别效果，其结果如图5所示。

表2 6部电台分类识别结果

图5 本文算法与参考算法的识别效果对比Fig.5 Comparison of the recognition results of the algorithm and the reference algorithm in this paper

从电台分类实验的结果来看，随着训练样本的提升，各算法在识别效率上都有一定程度的提升，本文提出的基于双谱融合的特征提取算法相较于其他方法有较大程度的提升。

4 结论

本文提出了基于双谱特征融合的特征提取算法。该算法对双谱切片特征提取算法进行了改进，将EMD分解引进了双谱切片特征提取中，通过对分解细化后的IMF提取切片的谱对称系数与分形特征，反映出通信辐射源内部的细微特征，并融合了对角积分双谱特征。实验分析表明：该算法较传统的积分双谱算法能够更加充分地利用双谱内在信息，并且在最终的识别效率上有较大程度的提升。

[1]孙娜. 通信电台细微特征研究[D]. 北京：北京邮电大学, 2010.

[2]Lukin V, Totsky A, Fevralev D, et al. Adaptive combined bispectrum-filtering signal processing in radar systems with low SNR[J]. Proceedings-IEEE International Symposium on Circuits and Systems, 2006.

[3]Lin ChinTeng, Lin JiannYow, Wu GinDer.A robust algorithm for word boundary detection in the presence of noise[C]//Speech and Audio Processing, IEEE Transactions on intelligent Transportation Systems， 2002.

[4]Orosco E, Diez P, Laciar E, et al. On the use of high-order cumulant and bispectrum for muscular-activity detection[J]. Biomedical Signal Processing & Control, 2015, 18:325-333.

[5]徐书华, 黄本雄, 徐丽娜. 基于SIB/PCA的通信辐射源个体识别[J]. 华中科技大学学报(自然科学版), 2008, 36(7):14-17.

[6]肖乐群，张玉灵，赵拥军.基于对角积分双谱的雷达辐射源信号识别[J].信息工程大学学报，2012,13(1):95-99.

[7]Tang L, Jiang T. Target identification based on diagonal slice of the complex bispectrum[C]// Communication Problem-Solving (ICCP), 2014 IEEE International Conference. IEEE, 2014:303-306.

[8]吴文，王金明，潘克修，等.基于六边形主域积分双谱的通信辐射源识别方法[J].军事通信技术，2012，33(2)：26-30.

[9]蔡忠伟,李建东 .基于双谱的通信辐射源个体识别[J] .通信学报,2007(2):75-79.

[10]马君国，肖怀铁，李保国，等.基于局部围线积分双谱的空间目标识别算法[J].系统工程与电子技术，2005,27(8):1490-1494.

[11]Huang Norden，Shen Zheng，Long Steven R.The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-stationary Time Series Analysis[C]//Proceedings of the Royal Society. London：1998,454:903-995.

A Transmitter Recognition Algorithm Based on Dual Spectrum Feature Fusion

GUI Yunchuan1,2, YANG Jun’an1,2，Wanjun1

(1.Electronic Engineering Institute of PLA ,Hefei 230037,China; 2.Key Laboratory of Electronic Restriction of Anhui Province , Hefei 230037,China)

In view of the problem that the identification method is not high and the intrinsic feature is difficult to be extracted, a feature extraction algorithm based on the bispectrum feature fusion was proposed .The feature vector was formed by the combination of diagonal integral bispectrum and the feature of bispectrum slice, and the original signal was decomposed by empirical mode decomposition; then the feature of the bispectrum slice was extracted from the instrinsic mode functions; finally the support vector machine was used to obtain the classification results. Six station classification experimental results showed that the proposed algorithm based on the bispectrum feature fusion integration was better.

communication transmitter; feature extraction; diagonal integral double spectrum; bispectrum slice

2016-03-15

桂云川(1991—)，男，江西鹰潭人，硕士研究生，研究方向：通信辐射源特征提取。E-mail:15209837812@163.com。

TN911.7

A

1008-1194(2016)05-0091-05