企业信息系统用户行为统计特性及其动力学分析

任佳佳，王念新，葛世伦

(江苏科技大学经济管理学院，江苏 镇江 212003)

0 引言

对用户访问行为规律的研究分析，是大型门户网站、社交网络、电子商务网站等每天必做的功课，通过对网站访问的分析研究，了解用户的地域分布、兴趣爱好、行为特征等，从而更好地对网站进行运维管理，改善网站的服务质量，以迎合客户需求，吸引客户。但是在管理信息系统领域中，企业缺乏对用户行为规律的研究，在新信息技术不断涌现特别是云计算的背景下，基于云的信息系统已成为必然［1］，对系统中用户行为规律和群体特征缺乏了解，会阻碍管理信息系统的发展。

通过对大量人类行为事件进行研究分析，从中挖掘出人类行为的特性与规律，是当前的研究热点之一，已在许多领域开展了大量的实证探索，取得了系列的研究成果，研究情境包括水路邮件［2-4］、电子邮件［5］、网页浏览［6］、电影点播［7］、手机通讯［8-10］、金融活动［11］、博客论坛［12-13］、面对面交互网络［14］等。然而到目前为止，对人类行为模式研究较少，仅有文献［11］研究了市场中的证券交易，文献［15］对某世界500 强企业下发采购订单行为进行了时间统计分析，但是对企业信息系统中的人类行为模式的研究还没有涉足。

为此，本文通过对企业管理信息系统用户访问日志数据进行分析，研究企业信息系统用户个人访问的时间间隔、活跃度、阵发性和记忆性，对信息系统中用户访问行为规律进行定量分析，并进一步研究群组用户和全体用户的访问时间间隔规律。研究企业信息系统用户访问行为的规律，可以对信息系统用户的访问行为进行有效预测，进而为企业信息系统的运行维护和优化提升提供依据，同时也拓展了用户访问行为规律的研究情境。

1 研究方法

1.1 人类行为动力学

全面深刻地认识复杂的人类行为特征一直是学者们努力的方向。以往由于数据记录的手段落后，加上缺乏现代统计工具和方法，在研究涉及人类行为特性的问题时，常常假设人类行为是符合泊松过程的稳态随机过程，其2 个相继行为的时间间隔用负指数分布描述如下:

泊松过程可以看作具有负指数间隔的计数过程，即人类活动模式是随机和平稳的，其相邻事件的时间间隔大体上是均匀的，很长的时间间隔非常稀少。

随着信息技术的发展和现代统计工具的进步，人类记录和分析自身行为数据的手段也越来越高效和便捷，使得利用大规模数据分析人类行为模式成为可能。2005 年，Barabási［2］在Nature 上发表了一篇题为“The origin of bursts and heavy tails in human dynamics”的论文，标志着人类行为动力学的正式提出，该论文通过分析电子邮件发送和回复行为的时间间隔，揭示了人类行为在时间上对泊松分布的偏离，人类行为的时间统计特性不是均匀的，其中伴随着长时间的静默和短时间内的高频率的爆发，相继行为的时间间隔分布具有明显的胖尾特征，可以用幂律分布函数更好地拟合，即:

人类行为动力学是一门新兴的交叉科学，通过对大量人类行为事件进行定量统计，从中挖掘人类行为的统计规律，提出假设建立模型来探索这些规律的产生机制和可能的动力学影响［2］。大量的实证研究都揭示了人类行为在时间维度上是偏离泊松分布的，在行为模式上表现出了短时间阵发和长时间休眠的特征。

1.2 时间特征分析指标

人类行为的时间特征指标分别包括间隔时间、活跃度、阵发性、记忆性等。

1)间隔时间:是指连续2 次相继访问的时间间隔。例:甲于“201211 08:08:08”时刻访问信息系统，乙在“201211 08:08:09”时刻访问信息系统，则甲乙2 个相连行为的间隔时间为1 秒。如果所有系统用户访问信息系统的次数为k 次，则有k-1 个间隔时间。本文的时间单位是秒。

2)阵发性:是描述用户行为短时期密集活动和长时间静默的物理量，在本文中使用Goh 和Barabási的公式计算阵发性，如公式(3):

其中，στ，mτ分别指间隔时间分布的标准差和平均值。对于指数分布，标准差和均值相等，所以阵发性为0;而对于严重的胖尾分布，标准差远大于均值，B接近1。

3)记忆性:是描述时间间隔特性的相关性程度，人类活动长的时间间隔后面容易跟着一个长的时间间隔，短的时间间隔后则容易跟着一个较短的时间间隔，这样的人类行为发生的时间序列被认为具有记忆性。把所有行为发生的间隔时间按时间发生先后排成序列，把前nσ-1 个间隔时间构成序列1，后nσ-1个间隔时间构成序列2，m1，m2分别为序列1 和序列2 的平均值，σ1，σ2分别为序列1 和序列2 的标准差，在本文中使用Goh 和Barabási［16］的公式计算时间序列的记忆性，如公式(4):

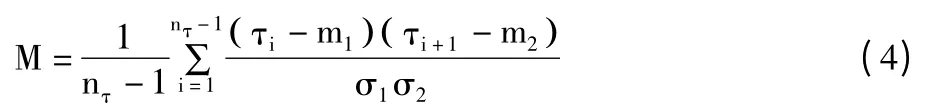
4)活跃度:即活跃程度，是指一个人从事某种活动的强度。文献［7］提出活跃度的概念，并指出了用户活跃性程度与幂指数具有非线性正比关系，定义活跃度为第一个行为发出到最后一个行为发出这段时间内用户发出的平均行为数。Ni是该用户个体发出的行为总数，Ti是该用户从第一个行为发出到最后一个行为之间经历的总时间，如公式(5):

2 数据收集与分析

2.1 样本企业的选择

在本文中以X 公司为研究对象，研究用户访问企业信息系统的时间特征。X 公司是国内著名的船舶修造企业，有员工及务工人员1 万多名。X 公司一直重视企业信息系统建设，曾投入巨资购买了Oracle的ERP 系统。由于受到全球经济危机的影响，船舶市场整体低迷，X 公司为了增强企业竞争力，于2011年9 月实施了成本管控系统，包含报价成本、目标成本、成本核算、成本分析、财务管理等共8 个子系统，该成本管控系统注册用户314 名，人均日访问量3次，人均日访问系统功能3 个，员工的访问人数和访问量代表了X 公司的信息化应用情况。

2.2 数据获取

从X 公司成本管控系统的数据库日志文件，提取了2011 年9 月14 日到2013 年6 月14 日期间用户对成本管控系统的访问操作，删除了没有登录名和部分错误的记录，得到了314 位系统用户共计348122 条访问行为记录，通过访问行为记录研究总体用户访问行为规律，同时以其中30 位访问量最大的活跃用户为对象研究个体用户访问行为特征，并对30 位活跃用户按访问量大小分为3 个群组，研究群组用户的访问行为特征。

用户的每条访问行为记录包含9 个元素(ID，UserID，LoginID，LoginName，LoginTime，LogoutTime，MachineID，MachineName，ModuleName)，分别表示序列号、用户号、登录号、登录名、登录时间、登出时间、机器号、机器名、功能模块。

2.3 数据分析

在对数据的获取和分析过程中，主要运用SQL Server，Matlab，Excel 等工具对样本数据进行处理和分析。

1)根据X 公司的数据库日志文件，提取所有用户登录访问系统时间，计算相继访问系统行为的时间间隔;

2)通过Matlab 软件，得到相继行为的间隔时间在双对数坐标下的概率分布图;

3)采用最小二乘法对主体数据拟合得到幂指数及其概率密度函数，选出30 位访问量最多的活跃用户分析用户访问行为特征并统计其访问量、活跃度、阵发性、记忆性等指标，同时将其分为3 个群组，从个体——群组——全体3 个层面研究信息系统用户访问的行为规律特性。

2.4 拟合方法及过程

数据拟合又称函数逼近，是指选择适当的曲线来拟合离散数据点，不要求经过所有数据点，只要求尽可能地反应数据点的基本走势。本文所用拟合工具是Matlab，拟合方法是最小二乘法，即根据已提取的数据找到函数关系表达式，作为拟合模型，使求解得到的数据和实际数据之间误差的平方和最小。对数据拟合的优劣性衡量指标有:解释能力(R-square)、残差平方和(SSE)、均方根(RMSE)等。其中残差平方和(SSE)是衡量最小二乘拟合优劣程度最重要的指标之一，R-square 越大，SSE 和RMSE 越接近0，说明模型选择和拟合效果好，数据预测也越成功。

笔者用Matlab 通过自己编写的代码，作出X 公司的成本管控系统用户的访问时间间隔在双对数坐标的图，然后通过最小二乘法在Matlab 下的实现，找出最优的拟合模型。

3 结果分析

3.1 个人行为分析

1.个体用户访问信息系统的规律。

以数据库日志文件中访问量最大的前30 位活跃用户为对象，通过Matlab 软件，得到这30 位活跃用户对成本管控系统访问行为的间隔时间在双对数坐标下的概率分布图，然后利用最小二乘估计方法对主体数据曲线进行拟合，得到个体用户访问信息系统行为的拟合曲线，图1～图3 分别是系统管理员、访问量排名第19 位和第21 位的用户访问系统相继行为的间隔时间分布。其中蓝色点为全体用户访问成本管控系统相继行为间隔时间的原始数据，红色直线是拟合曲线，3 位用户访问信息系统相继行为的幂律分布指数分别为0.9622，0.6422 和0.6787。

综上分析，发现个体行为的时间统计特性不是均匀的，其中伴随着长时间的静默和短时间内的高频率的爆发，相继行为的时间间隔分布具有明显的胖尾特征，其间隔时间分布在超过2 个数量级范围服从幂律分布P(τ)～τ-α，幂指数不等。

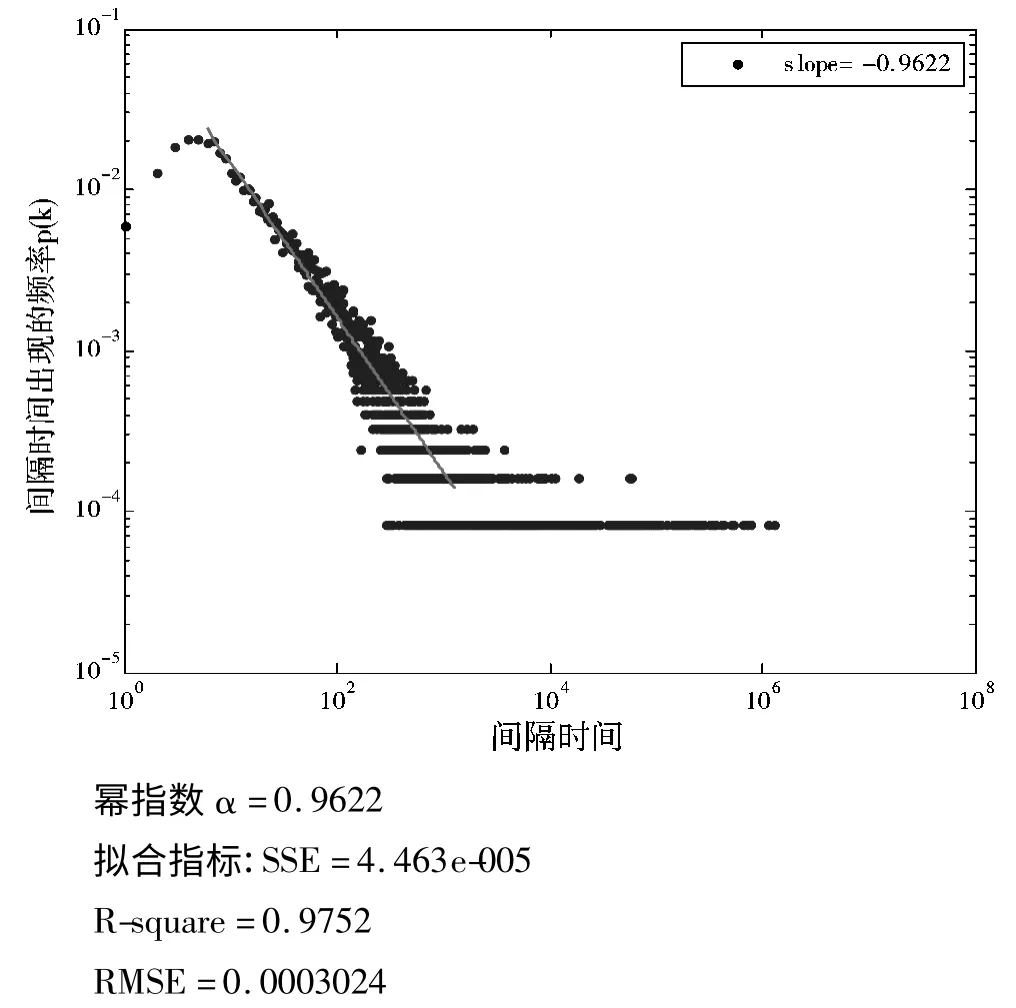
图1 系统管理员的间隔时间概率分布图

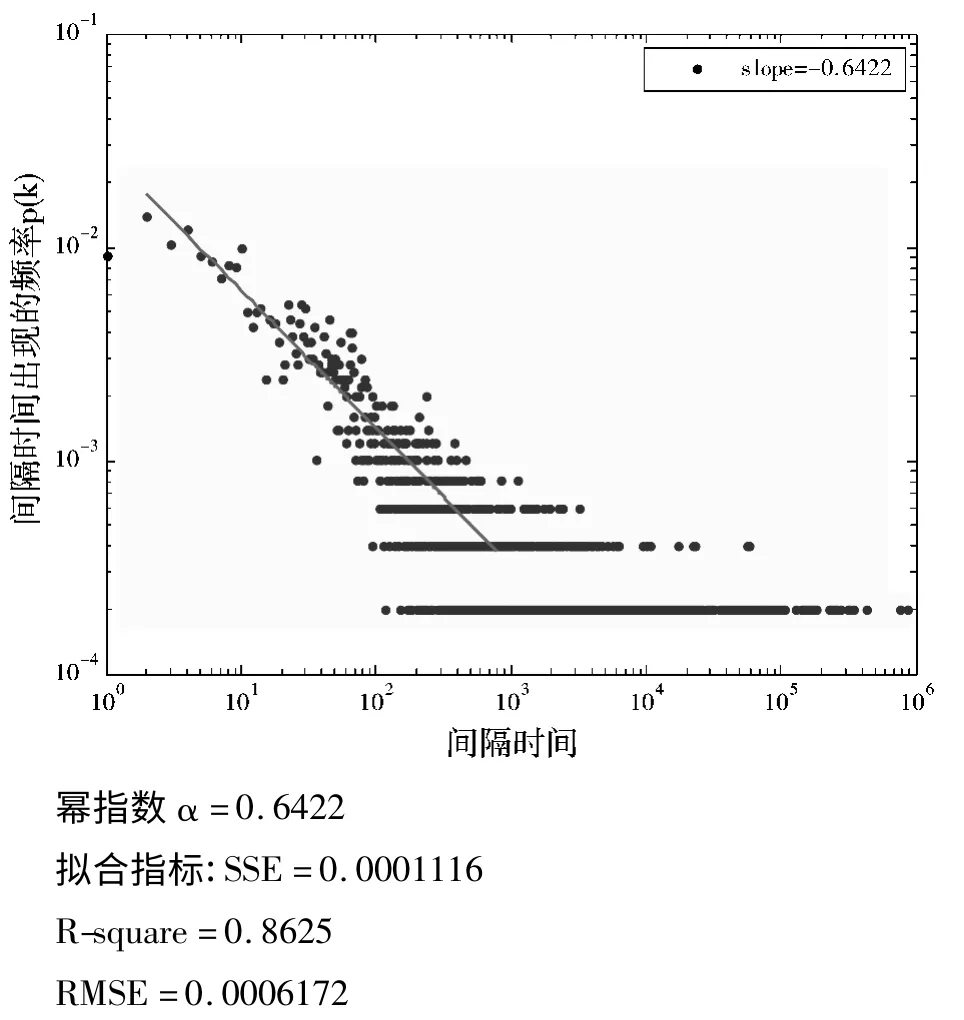
图2 访问量排名第19 的用户的间隔时间概率分布图

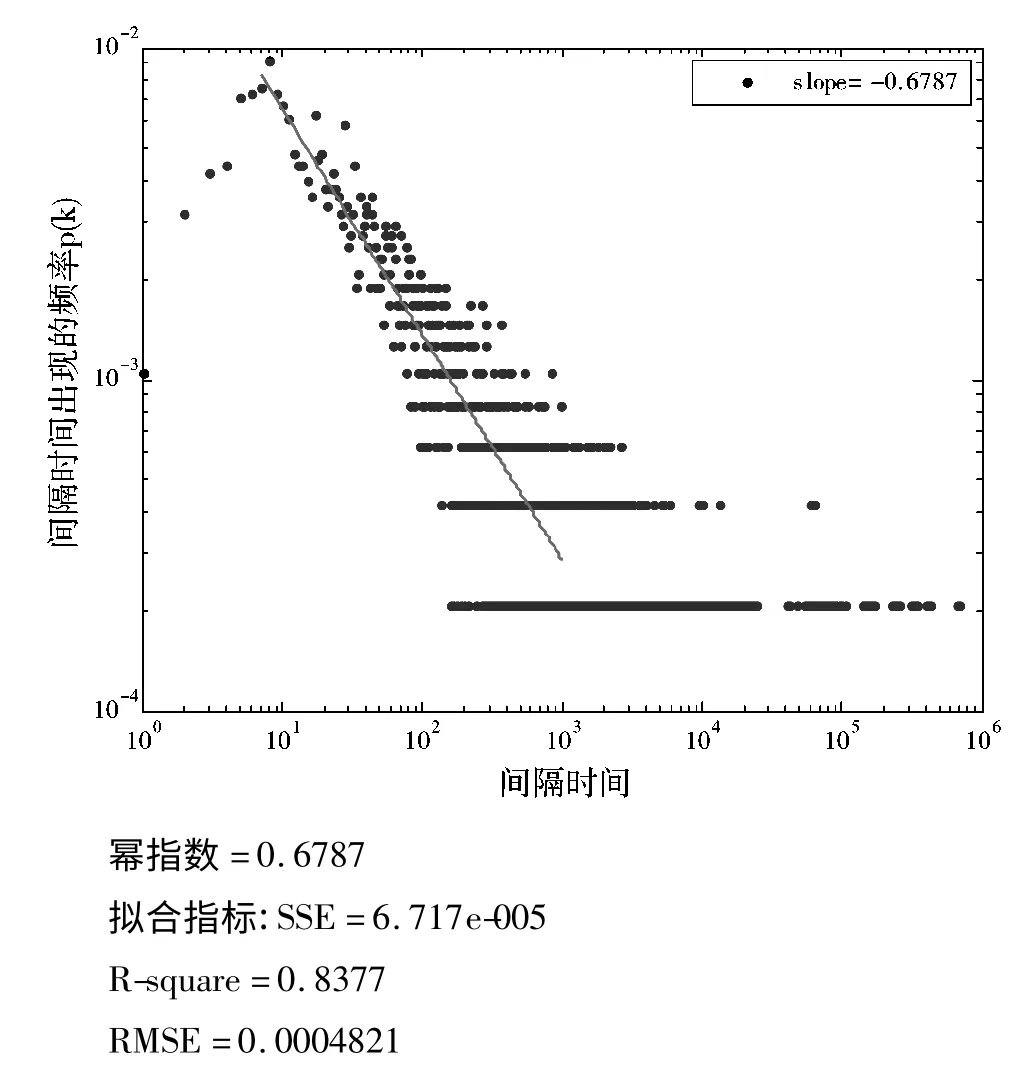
图3 访问量排名第21 的用户的间隔时间概率分布图

2.活跃度和幂指数之间的关系。

人类行为是高度复杂的，用户的行为规律不仅体现在间隔时间的分布规律上，为了更深层次挖掘信息系统用户的访问行为规律，本文对30 位用户的访问间隔时间的阵发性、记忆性和活跃度指标进行计算，详见表1。从表1 可以发现:

1)X 公司个人用户对成本管控系统的访问行为表现出强阵发性和弱记忆性，相比其他研究的复杂行为中的阵发性值，本系统中个人访问行为表现出来的阵发性值更大，说明企业信息系统用户访问的胖尾更为严重。

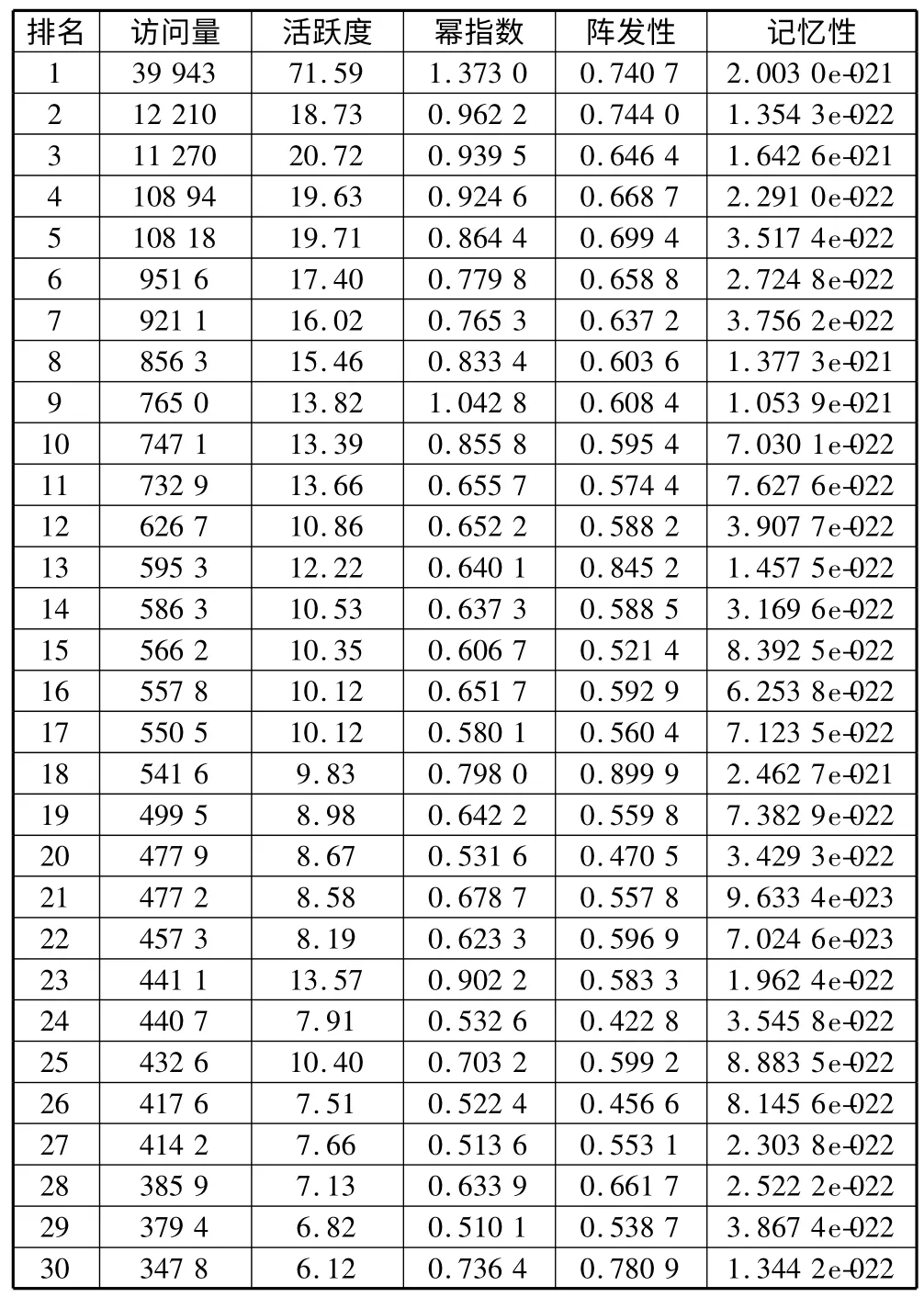
表1 30 位活跃用户

2)幂指数和活跃度存在正相关关系，幂指数会随着活跃度增加而增加，但是幂指数不会无限增大，大概到1.5 左右时会保持稳定，如图4 所示。例如个人访问量最大的用户活跃度也最大，每天接近72 次访问管理系统，但是幂指数是1.37。

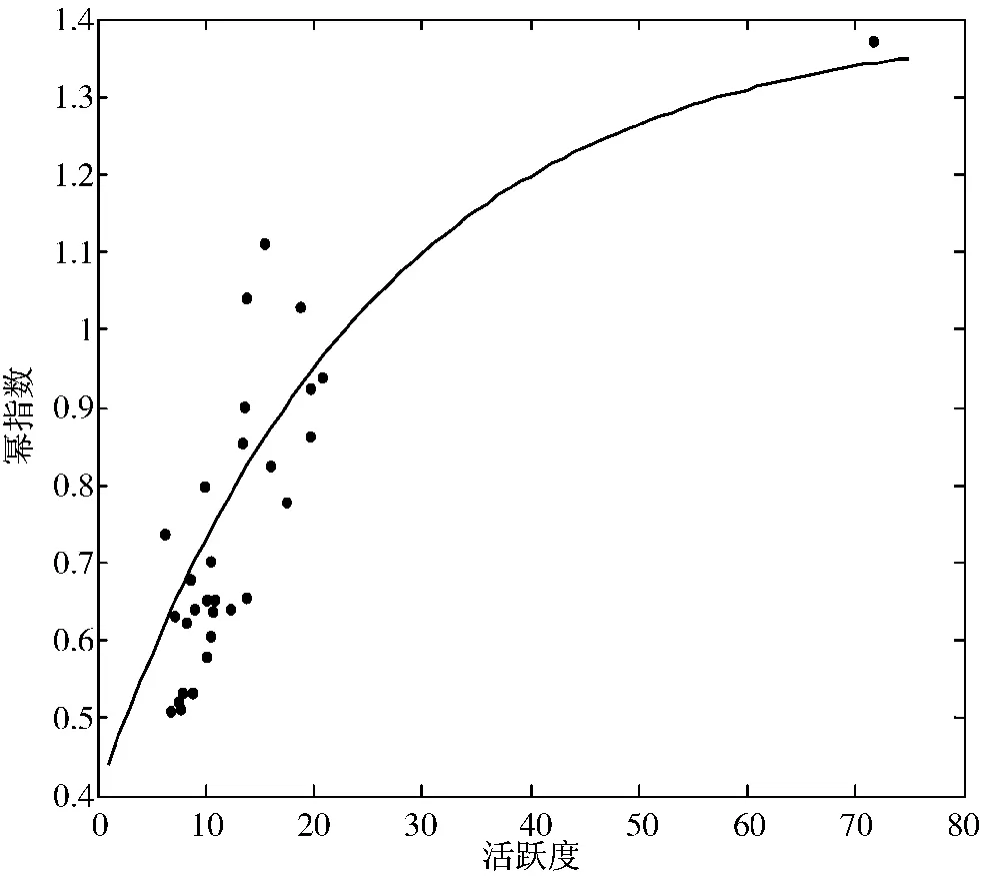
图4 个体用户访问行为活跃度和幂指数关系图

3.2 群组行为分析

为了研究群组访问信息系统的行为，把30 位活跃个体用户按照访问量的大小递减排序，把排序后的用户分为3 个群组，每个群组包含10 个用户，群组数据按照对成本管控系统访问时间的先后顺序组成。首先利用幂律分布分析3 个群组对成本管控系统访问行为时间特性，如图5～图7 所示。虽然3 个群组幂律分布的拟合指数较好，但是对3 个群组的拟合中没有考虑头部的数据，而群组数据由于数据量大且并发严重，不能不考虑头部，从图5～图7 中也可以看出头部显然是偏离幂律分布的。所以，群组用户访问信息系统的间隔时间可能不是服从单一的分布。

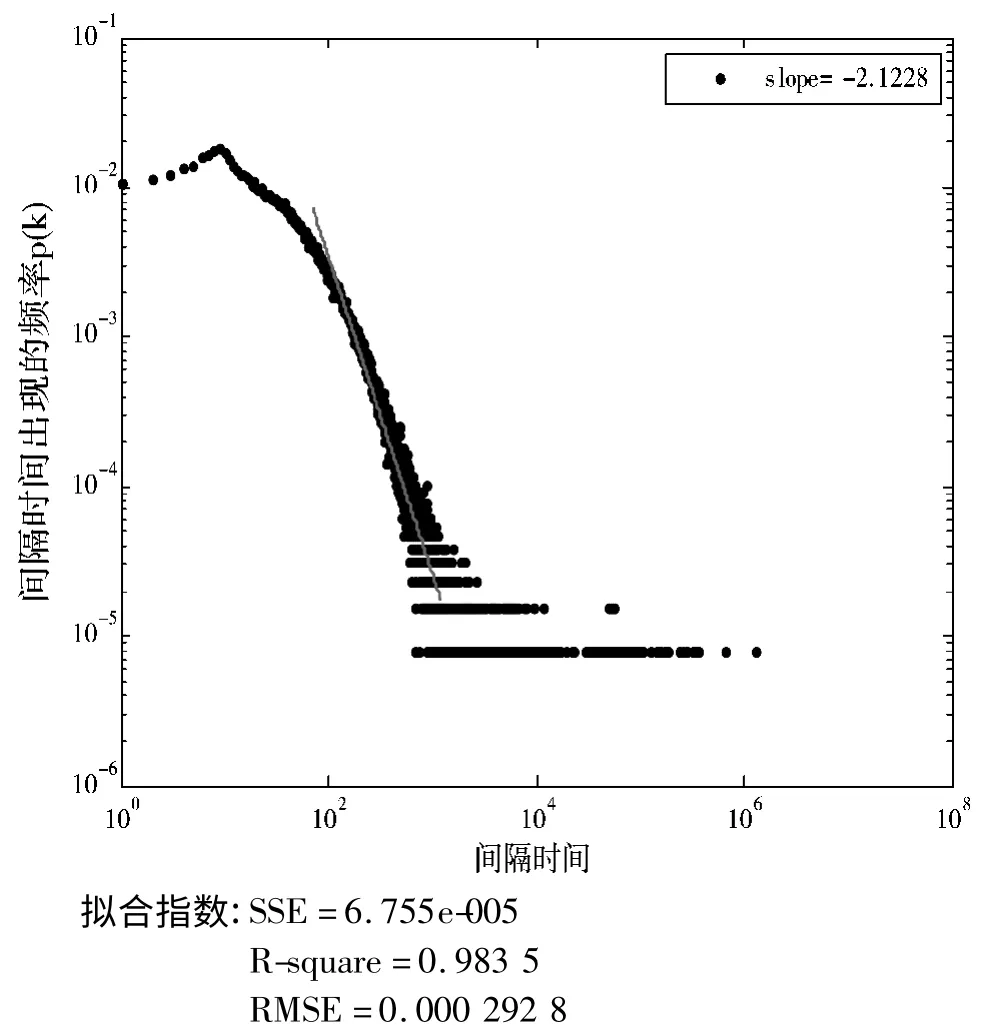
图5 群组1 的间隔时间幂律分布图

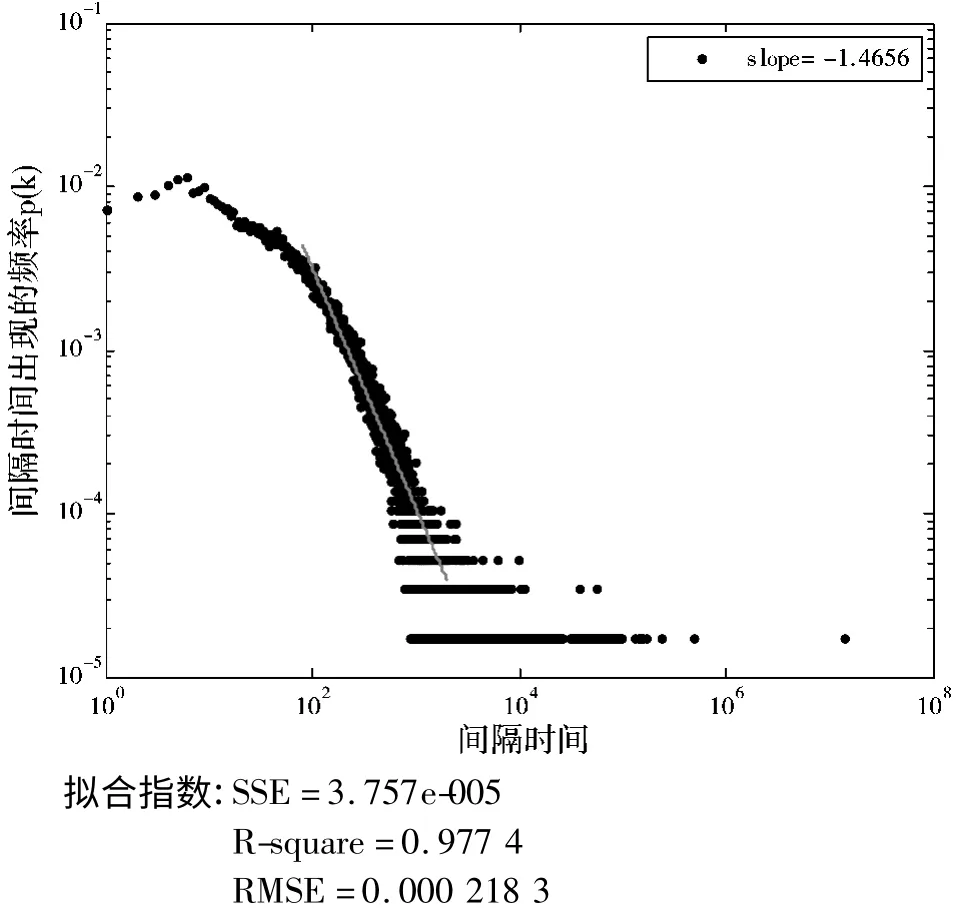
图6 群组2 的间隔时间幂律分布图

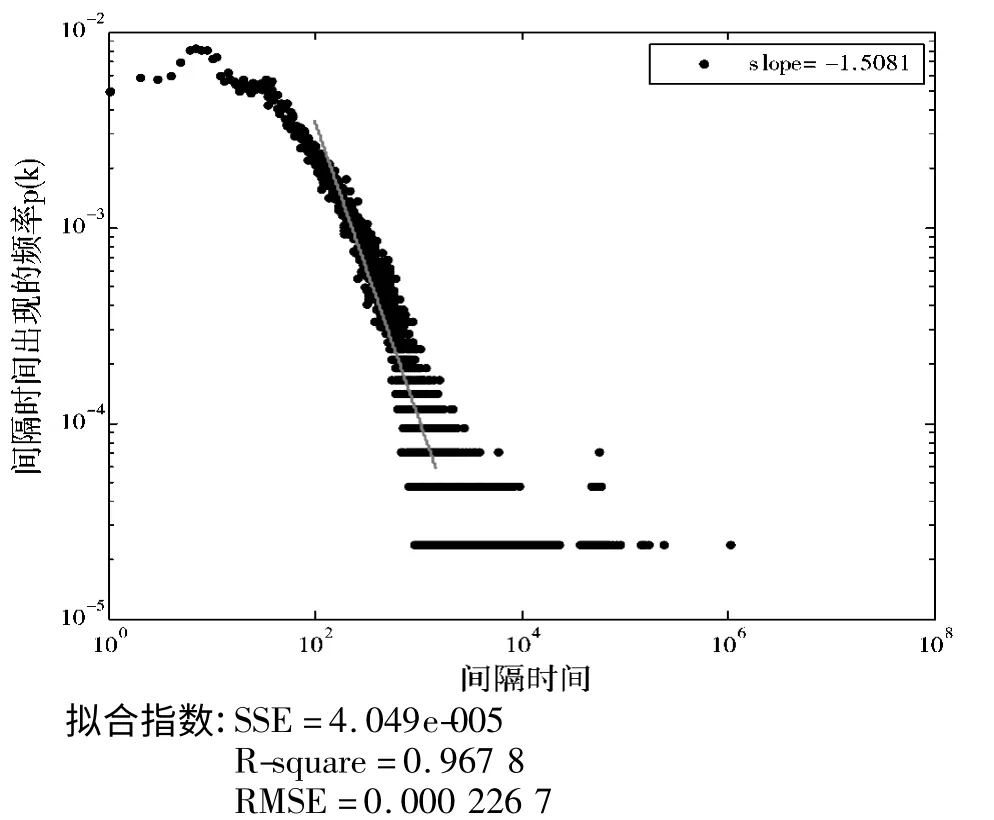
图7 群组3 的间隔时间幂律分布图

为了更加精准地拟合群组数据，本文采用指数分布与幂律分布的混合分布，即带指数截断的幂律分布，对3 个群组的数据重新进行拟合，拟合函数如下:

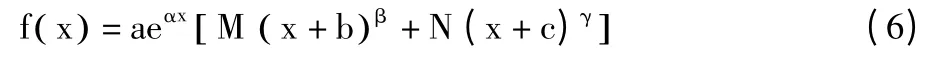
拟合结果如图8～图10 所示。

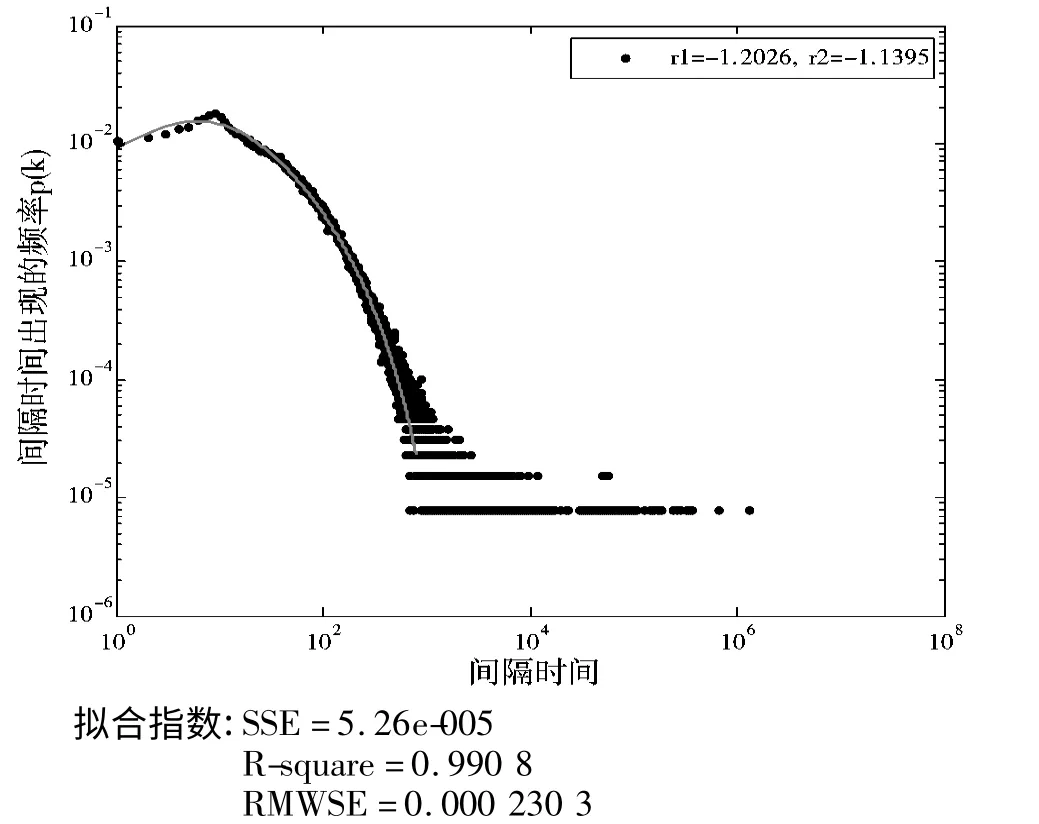
图8 群组1 的间隔时间混合分布图

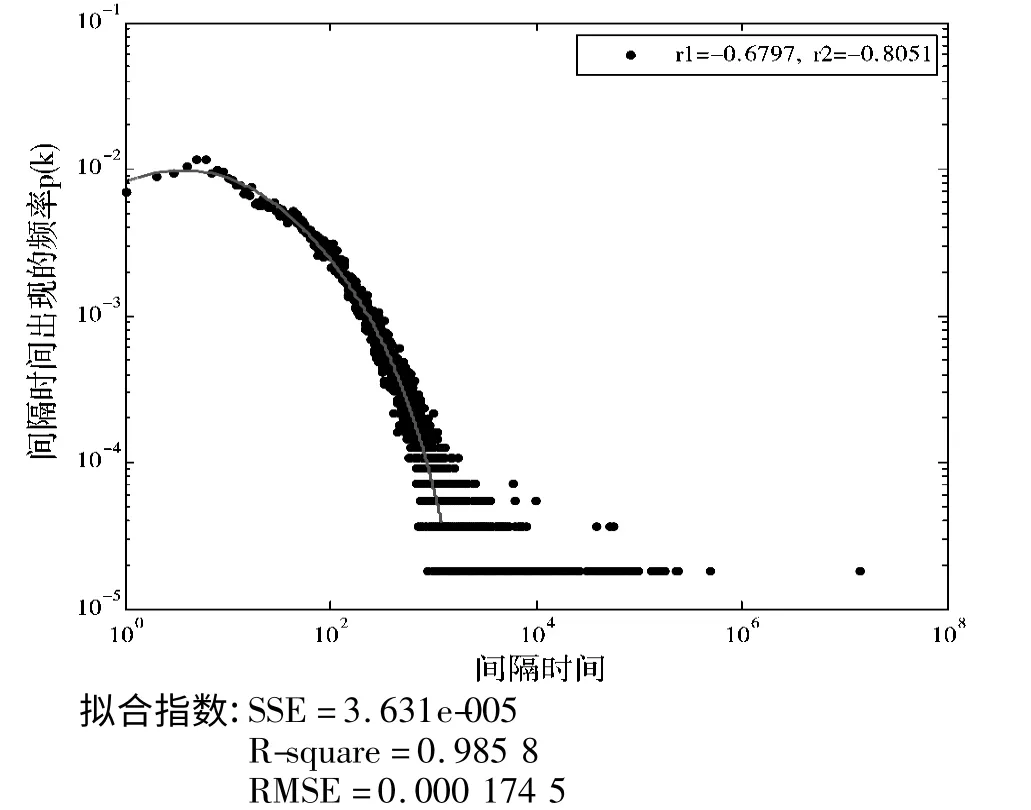
图9 群组2 的间隔时间混合分布图

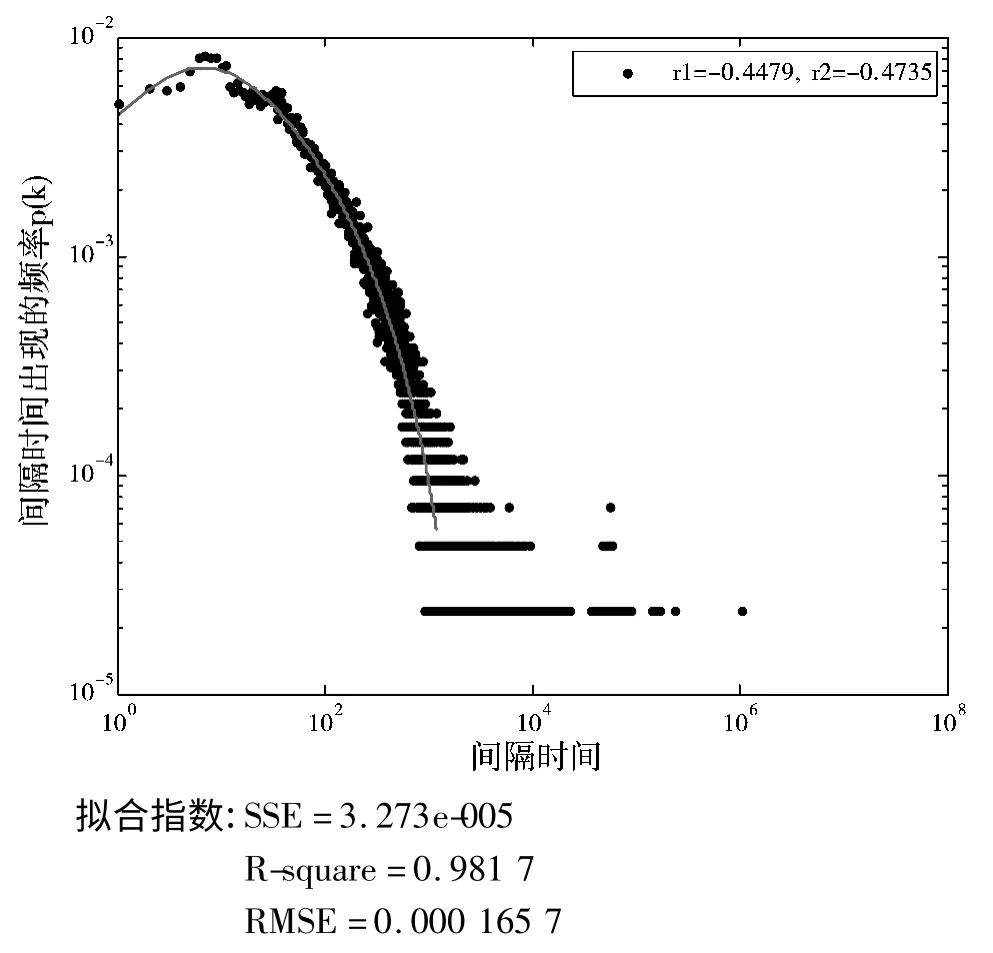
图10 群组3 的间隔时间混合分布图

从图8～图10 可以看出，相比单纯的幂律分布，混合分布的拟合指数更优，对3 个群组用户访问信息系统的行为拟合更加精准。为什么服从幂律分布的个体叠加，为什么会偏离幂律分布?一方面是因为对个体用户访问行为头部数据的忽略，这些忽略偏差的累积导致了群组访问行为产生了指数因子;另一方面是信息系统员工访问行为的特性，个体用户很少会在10 秒内大量并发地访问信息系统，在对个人访问行为数据统计时发现，虽然有10 秒内连续访问信息系统的情况，但是这包含了一定的误操作和非规范操作，所以在对个人用户访问行为的间隔时间分布拟合时，没有考虑间隔时间在10 秒内的情况，而对于群组的数据则不然，每天对信息系统的访问交叉在一起，存在大量的并发情况，导致小的间隔时间所占比例增加，从图中也可以看到小的间隔时间出现概率增大，同时由于每个群组数据只包含了10 个个体用户，数据量相对不是很大，导致10 秒内的并发情况近似平缓，正如图8～图10 中所展示的，体现了一定指数分布的特性。

此外，通过对3 个群组数据拟合得到的幂律分布函数，对比混合分布所包含的2 个幂律部分，可以发现群组1 的幂律指数最大，而群组3 的幂律指数最小，这是源自用户活跃程度的不同所造成的，群组1包含的访问行为数据最多，整体活跃性程度最大，每天的并发访问情况最大，导致小的间隔时间所占比例大于另外2 组，大的间隔时间所占比例则小，从而导致在幂律指数在3 组中是最大的。而群组3 正好相反，整体的活跃性程度在3 个群组中最小，即并发访问情况相对较轻，小的间隔时间所占比例小，大的间隔时间占的比例大，即体现在幂律指数是3 个群组中最小的。

3.3 全体行为分析

3.1 节和3.2 节对管理信息系统的个体用户访问系统行为规律进行了统计和分析，对分成3 个群组的个体用户进行了群组访问行为规律的分析，得到了与个体用户行为不同的群组特性。下面将从数据库日志文件中获得的访问行为数据进行整体研究。

研究发现，虽然全体行为的间隔时间分布在超过2 个数量级范围服从幂律分布P(τ)～τ-α，但是实证数据的头部显然兼具着指数分布的特性。用指数截断的幂律分布对数据进行拟合，发现拟合参数中的R2值仅为0.501 2，如图11 所示，没有找到合适的指数截断的幂率函数形式，所以除了混合形式的分布，用分段形式的分布来表示更好。如图12 所示，头部的数据用指数分布拟合，中尾部的数据用幂律分布拟合，拟合曲线和实证数据高度吻合。

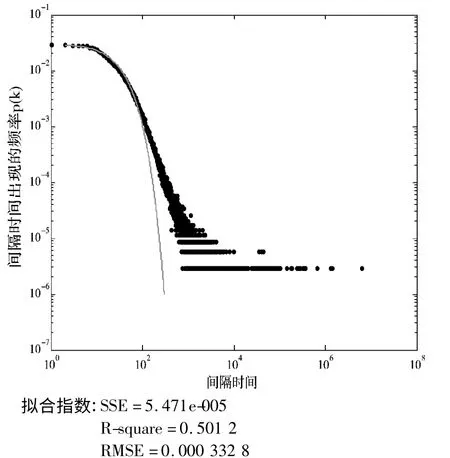
图11 全体用户访问的间隔时间混合分布图

从图中可以看到，在60 秒内的间隔时间服从指数分布，超过60 秒后的间隔时间服从幂律分布。由于相对只有10 个个体用户访问行为数据的群组而言，全体访问有314 位用户，每个工作日都会有更严重的并发访问信息系统。从图12 中也可以看到，小的间隔时间概率在增大，从而导致对比个体用户和群组访问行为的间隔时间，全体访问行为间隔时间数据的头部更加的平缓，更加趋向指数分布，从拟合效果也可以看到，60 秒内间隔时间用指数分布拟合和实证数据的吻合(R2=0.999 1)，即全体用户在60 秒内对成本管控系统的访问服从泊松分布;而随着间隔时间的增大，分布逐渐偏向幂律分布(R2=0.989 9)，幂指数是2.268 9。对比个人访问行为，全体访问行为数据中段部分的幂律分布指数更大，原因是随着访问人数的增多，并发访问变大，小的访问间隔时间所占比例增大，大的间隔时间所占比例变小，导致幂指数变大;全体用户的访问行为的间隔时间在头部出现较大差异，一方面是由于对个体行为拟合的弱小误差，另一方面是并发情况的加剧所导致。所以，可以大胆设想，如果系统用户有无穷多个用户，日常访问的并发情况应该更严重，可能会导致访问行为60 秒内的间隔时间分布也偏离指数分布，趋向幂律分布。

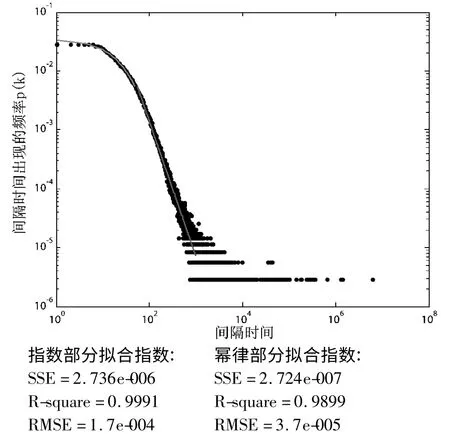
图12 全体用户访问的间隔时间分段分布图

4 结论与讨论

通过对信息系统用户的个体——群组——全体3 个层面的实证分析，探讨系统用户访问行为特征，实证结果表明:

1)信息系统用户行为的统计规律在个体层面上表现出单一的幂律分布，在群组层面具有混合分布的特征，在全体层面却表现出分段的分布形态，展现了人类行为的高度复杂性和多重标度特性。

2)信息系统用户在个体——群组——全体3 个层面都表现出了严重的胖尾特征，个体用户的访问有很强的阵发性和弱记忆性，幂指数和活跃度存在正相关关系。

3)个体——群组——全体3 个层面表现出的幂律指数的差异，是由并发访问情况的差异所决定，并发性越大则小的间隔时间所占比例越大，大间隔时间所占比例则小，幂指数越大。

笔者得到和以往学者针对用户行为研究的不同:信息系统用户的访问行为在个体到群组再到全体展现出不同的标度特性，表现出人类行为的高度复杂性，对于用户行为的规律的研究有更深层次的意义，为了更加深刻地理解人类行为提供一定的理论和实证提供一定的参考价值。同时仍有一些问题值得进一步研究，比如，笔者指出了用户行为的幂律特征和用户的并发访问有深刻的联系，并发访问的严重程度决定了幂律指数和泊松特征，需要扩展数据量来实证分析;另外分析用户对信息系统的使用频度，对各个功能业务模块访问的差异性等;同时建立一个信息系统用户访问行为的动力学模型来预测用户行为也是笔者急需解决的问题。

［1］Petter S，DeLone W，McLean E R.The past，present，and future of“IS Success”［J］.Journal of the Association for Information System，2012，13(5):341-362.

［2］Barabási A L.The origin of bursts and heavy tails in human dynamics［J］.Nature，2005，435(7039):207-211.

［3］Oliveira J G，Barabási A L，Human dynamics:Darwin and einstein correspondence patterns［J］.Nature，2005，437(7063):1251.

［4］李楠楠，张宁，周涛.人类通信模式中基于时间统计的实证研究［J］.复杂系统与复杂性科学，2008，5(3):43-47.

［5］Johansen A.Probing human response times［J］.Physica A:Statistical Mechanics and Its Applications，2004，338(1-2):286-291.

［6］Vázquez A，Oliveira J G，Dezsö Z，et al.Modeling bursts and heavy tails in human dynamics［J］.Physical Review E，2006，73(3):036127-1-036127-19.

［7］Zhou Tao，Kiet H A T，Kim B J，et al.Role of activity in human dynamics［J］.Europhysics Letters，2008，82(2):28002.

［8］Candia J，Gonzalez M C，Wang P，et al.Uncovering individual and collective human dynamics from mobile phone records［J］.Journal of Physics A:Mathematical and Theoretical，2008，41(22):224015.

［9］顾亦然，谢鸿飞，李金发.移动通信网络中人类行为动力学的研究［J］.计算机技术与发展，2010，20(9):57-60.

［10］Jiang Zhiqiang，Xie Wenjie，Li Mingxia，et al.Calling patterns in human communication dynamics［J］.Proceedings of the National Academy of Sciences of the United States of America，2013，110(5):1600-1605.

［11］Scalas E，Kaizoji T，Kirchler M，et al.Waiting times between orders and trades in double-auction markets［J］.Physica A，2006，366:463-471.

［12］Guo Jin-li.Weblog patterns and modeling human dynamics with decaying interest［J］.Computer Science.2010，1008.0042v3.

［13］闫小勇，吴联仁，郑兰.微博社区中用户行为特征及机理研究［J］.电子科技大学学报，2013，42(3):328-333.

［14］Starnini M，Baronchelli A，Pastor-Satorras R.Modeling human dynamics of face-to-face interaction networks［J］.Physical Review Letters，2013，110(16):168701-168701-5.

［15］Gao Lei，Guo Jin Li，Fan Chao，et al.Individual and group dynamics in purchasing activity［J］.Physica A:Statistical Mechanics and its Applications，2013;392(2):343-349.

［16］Goh K I，Barabási A L.Burstiness and memory in complex systems［J］.Europhysics Letters，2008，81(4):48002-P1-48002-P5.