基于矩阵约简的Apriori 算法改进

2015-11-26任伟建于博文

计算机与现代化 2015年9期

任伟建，于博文

(东北石油大学电气信息工程学院，黑龙江大庆 163318)

0 引言

关联规则的挖掘是数据挖掘领域中的一个重要研究方向，旨在从海量数据中发现隐藏的关联关系、人们感兴趣的数据集合和与指定数据相关联的数据，来辅助人们快速做出决策。Apriori 算法则是挖掘关联规则的经典算法，其核心思想是通过扫描数据来获取频繁项集，然后根据得到的频繁项集生成关联规则。但Apriori 算法自身存在2 个主要缺陷［1］:1)Apriori 算法需要多次地重复扫描数据库，当有海量数据信息时会造成严重的输入输出负载;2)在查找频繁项集时会生成很多无实际操作价值的候选项集，占据大量存储空间。

许多学者针对Apriori 算法的现有缺陷提出了诸多改进思路，以提高Apriori 算法的执行效率。在文献［1］中，提出了基于数组的挖掘方法，降低了扫描数据库的次数，将多维数据存储在与之对应的数组中，在查找k-项集时，只需对数组维数不小于k 的数组进行扫描，但其依旧有大量的重复扫描操作，效率较低。在文献［2］中，提出基于向量的挖掘算法，该算法需要将数据中的事物和项目采用向量表示，通过遍历获取频繁k-项集，但所转换的向量占据了大量的存储空间。在文献［3］中，提出基于矩阵的挖掘算法，算法将数据信息转换成矩阵形式，其原事务转换为行，原项集转换为列，在矩阵中可以一次性生成所有频繁集或者候选集，但该算法同时也会生成大量没有操作价值的候选集。

综合上述算法，本文提出一种基于矩阵约简的Apriori 改进算法，通过对数据库进行一次扫描，建立与数据库对应的事务布尔矩阵，无需再对数据库进行扫描，降低原Apriori 算法对数据库扫描的次数，以及数据库的输入输出负载;用计算速度较快的向量间“与”运算和对矩阵的约简，简化原算法中的连接和剪枝步骤，减少候选项集的生成个数;随着频繁k-项集的生成，k 值越大其所对应的矩阵结构越简单，从而提高算法的执行效率。

1 关联规则Apriori 算法分析

Apriori 采用传统的迭代算法，通过频繁k-项来生成频繁(k +1)-项集。算法首先需要确定频繁1-项集，利用生成的频繁1-项集去找寻频繁2-项集，再利用生成的频繁2-项集去找寻频繁3-项集，以此类推，直到无法找到频繁k-项集，在算法执行的过程中查找每个频繁项集都会对数据库进行一次扫描。

Apriori 算法中，频繁项集中所有的非空子集都为频繁项集，算法根据这一特性查找频繁项集。在算法的连接步骤中将2 个频繁(k-1)-项集连接产生大量的候选项集，在算法的剪枝步骤中利用频繁项集的特性除去那些包含非频繁项集的候选项集，生成频繁k-项集。算法在每次连接和剪枝的过程中都会扫描多次数据库，假设生成的频繁项集中包含m-项集，在此过程中则需要对数据库进行m 次扫描，大大增加了输入输出负载。在随后的算法迭代过程中候选项集的个数成指数级增长，将会生成大量无实际操作价值的候选项集，很大程度影响了Apriori 算法的执行效率。

2 Apriori 算法的改进

2.1 定理证明

项目数和支持数:在数据库DB 对应的“0”、“1”矩阵中，每一行代表一个事务，所以该行中“1”出现的次数即为该事务中的项目数。每一列代表一个项目，所以该列中“1”出现的次数即为该项目的支持数。通过对矩阵中的列向量进行与运算即可求得该项目的支持数。

1)DB 中的项集Ij为:

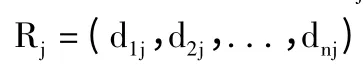
2)项集Ij的支持数为:

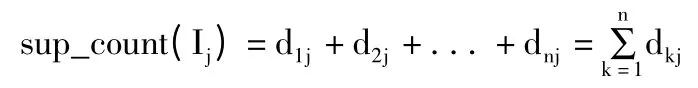
3)2-项集{Ii，Ij}的内积为:

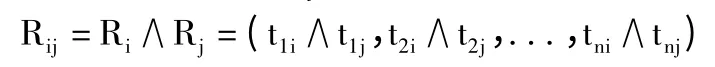
4)2-项集{Ii，Ij}支持数为:

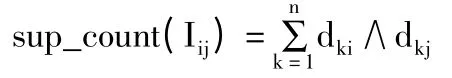
5)k-项集{Ii，Ij，...，Ik}的内积为:

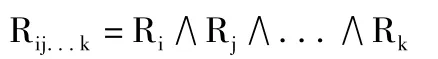
6)k-项集支持数为:

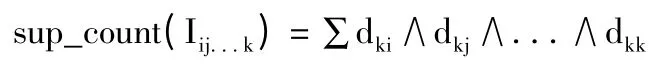
笔者根据项目数和支持数的概念及Apriori 算法的性质，给出如下定理:

定理1 矩阵中项Ij在频繁(k-1)-项集出现的重复次数若小于k-1，则可以直接从矩阵中去除与该项所对应的列。

证明:如果频繁(k-1)-项集中包含的候选(k-1)-项集子集的个数小于k，则k-项集不是最大频繁项集。由此得出频繁k-项集的集合元素在k-1 维数的频繁集出现的次数大于等于k-1。通过除去Ij所对应列的矩阵验证，在频繁(k-1)-项集中每个项集Ij出现的累积数都为k，从而说明含有Ij的k-1 候选项集都包含在频繁(k-1)-项集中，所以删除该列对挖掘结果没有影响。

定理2 在矩阵中若某一行的项目数小于k，则在求频繁k-项集时，可以直接删除该行。

证明:因为在求频繁k-项集的支持度时需要进行矩阵内列之间的与运算，计算与运算时只有所有元素均为“1”时，输出结果才为“1”。如果某行的项目数小于k，则该行中对应“1”的元素数必定小于k，在与其他行计算与运算项集的项目数必定小于k，因此可以直接删除该行。

定理3 当频繁k-项集集合中项集的个数小于(k+1)，则称频繁k-项集为最大频繁项集。

证明:在候选项集中的非空子集的支持数大于等于最小支持数的项集即为频繁项集，频繁项集中不在被其他项集包括在内的即为最大频繁项集。根据频繁项集的子集一定为频繁项集这一性质，频繁(k +1)-项集的一定有频繁k-项子集，而频繁(k+1)-项集的频繁k-项子集一定不少于=k +1)个。如果频繁k-项子集的个数小于k +1，则该事务数据库的最大频繁项集为频繁k-项集。

2.2 改进的Apriori 算法

由于Apriori 算法存在重复扫描数据库和产生大量无实际操作价值的候选项集的明显缺陷，提出基于矩阵约简对Apriori 算法进行改进，用矩阵Rm×n代替原数据库DB，根据上述项目数和支持数进行向量间运算求取候选项集的支持数，以此为依据确定频繁项集;根据上述定理对矩阵进行约简，简化原算法中的连接和剪枝步骤，降低数据库的输入输出负载，提高生成频繁项集的速度;为了提高算法效率，将矩阵中的各项按其支持数降序排列。

2.2.1 频繁k-项集的生成

根据上述改进思路制定如下频繁k-项集(k ＞2)的生成步骤:

1)首先扫描数据库生成与数据库对应的“0”、“1”矩阵R，为了方便后续计算，矩阵行为事务，列为项集。将包含m 条事物和n 个项目的事物数据库DB 转换成事物矩阵Rm×n。

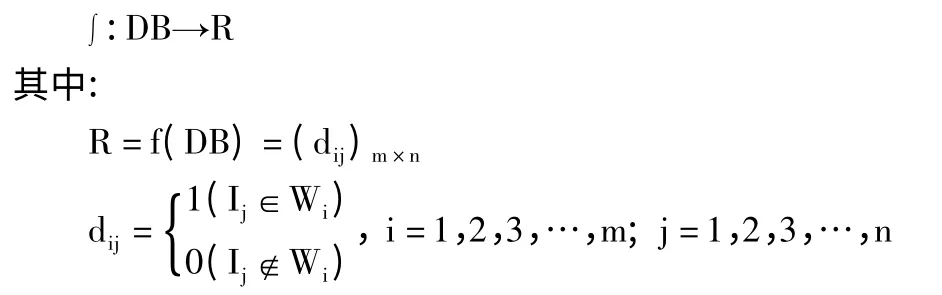
事物矩阵Rm×n中行代表事物，列代表项目，当事物Wi中包含项目Ij时，矩阵中对应的dij=1，否则dij=0。由于要对矩阵进行化简，在矩阵后方添加一列用来计算行合计(sum_hang)，即事务项目数;在矩阵下方添加一行用来计算列合计(lie_hang)，即项目支持数。

2)根据所给支持度确定最小支持数min_sup，通过向量间的“与”运算计算各项的支持数sup，对比矩阵的合计列数值，如果某项合计值小于min_sup，则删除该项所对应的矩阵列，余下的各项则是频繁1-项集。重新计算矩阵的行合计，若某事务的合计值为0，可直接删除该事务在矩阵中所对应的行，重新排序得到矩阵D1。

3)对矩阵D1进行结构约简，以便生成新的频繁k-项集。在生成频繁k-项集时，根据定理1 从矩阵中除去频繁(k-1)-项集中重复次数小于k 的项Ij所对应的矩阵列。重新计算矩阵的行合计，根据定理2，若事务数目的合计值小于k，则删除该事务在矩阵中所对应的行。重新计算矩阵的列合计，某个列合计小于min_sup 则删除矩阵中该元素所对应的列;按上述步骤重复化简矩阵结构，直到不能化简为止，得到矩阵Dk。

4)为了方便记录生成频繁k-项集的结果，为矩阵Dk设置一个辅助存储矩阵(设计成N×3 的矩阵，第1 列用来存储频繁k-项集的组合，第2 列用来存储事务支持数，第3 列用来存储项集个数)，主要存储频繁项集的组合和其出现的次数。按照k-项集来组合所对应的矩阵列，并一一对各个组合中的k 个向量进行“与”运算，然后统计“1”的个数，确定k-项集的支持数。根据计算结果，若k-项集的支持数大于等于min_sup，则该k-项集为频繁k-项集。将结果存在辅助存储矩阵中，按照其设计的方式存储信息。

5)根据定理3，当频繁k-项集集合中项集的个数小于(k+1)，则称频繁k-项集为最大频繁项集，终止此查找频繁项集的过程;若频繁k-项集集合中项集的个数不小于(k+1)，则重复步骤3)～步骤4)直至满足定理3 的条件。

通过上述步骤得到频繁k-项集，有效降低了原Apriori 算法对数据库的扫描次数，对矩阵的约简也避免了生成较多没有操作价值的候选集。

2.2.2 算法流程

输入:事务数据库DB;最小支持数min_sup

输出:数据库内事物的关联规则S

1)扫描事务数据库DB，生成与原数据对应的“0”、“1”矩阵R，计算矩阵R 的每一行及每一列中“1”的合计值，以此作为事务和项目的支持数求取频繁项集。删除列合计小于最小支持数的矩阵列，余下的即为频繁1-项集所对应的矩阵列，将矩阵列按支持数降序排列组成矩阵R1。

2)从R1矩阵中抽取任意矩阵列进行两两组合，通过向量间的“与”运算求取该组合的支持数，以此作为依据确定频繁2-项集。然后根据定理1 和定理2 对矩阵R1进行约简，重新排序后得到矩阵R2。

3)在确定频繁k-项集时(k ＞2)，按照2.2.1 节中叙述的频繁k-项集生成步骤3)～步骤5)执行，直到算法生成的频繁k-项集结果符合定理3，则此频繁k-项集即为最大频繁项集。

4)由频繁项集L 所生成的其所有非空集S，若某个集合S 和频繁集L 的支持数比值大于预设定的最小置信度，则可以生成强关联规则，即“S→L-S”。

2.3 算法分析

与传统Apriori 算法进行对比，改进的Apriori 算法优点如下:

1)通过上述算法的描述可以看出，改进的Apriori 算法只需对数据库进行一次扫描，生成与原数据库对应的事物矩阵(Rm×n)，之后的操作都是基于矩阵完成的;在生成频繁项集时，通过矩阵中列向量间的“与”运算求取候选项集的支持数，向量间计算的效率非常高的。根据项集组合的支持数确定频繁项集，生成频繁k-项集的时间复杂度为O(mkn);传统Apriori 算法在挖掘频繁k-项集时需要扫描k 次数据库，在“连接”和“剪枝”的过程中也需要重复扫描数据库，增加了数据库输入输出的负担，这一过程浪费了大量的系统资源，其生成频繁k-项集的时间复杂度为O(Wk+1)，在实际应用中w 的数值远远大于m;随着频繁k-项集的生成，k 值的增加使得与其对应的矩阵Dk结构越来越简单，减少相对不必要的计算量。

2)改进的Apriori 算法采用“0”、“1”矩阵代表对应的数据库信息，算法中的布尔变量占用的存储空间相对较少，大大减少数据信息所占用的存储空间。传统Apriori 算法在“连接”和“剪枝”的过程中产生大量的候选项集，造成了一定的存储空间浪费，而改进的Apriori 算法在生成频繁k-项集时，只需根据定理1和定理2 扫描行合计值大于等于k 的矩阵元素和矩阵中项在频繁(k-1)-项集出现的重复次数大于等于k-1 的矩阵元素，其他不符合条件的矩阵元素可以直接删除，对事务矩阵进行了约简，缩小了候选项集的生成规模，比原有算法占据更少的存储空间。

3)改进的算法将原有的数据库扫描过程转换成对内存的扫描，使数据扫描的效率得到了提高，并充分利用矩阵的结构信息简单易于操作的特点，根据上述定理对矩阵结构进行约简，查找频繁项集。

3 算法实验结果

3.1 实例分析

从UCI 数据集中的Thyroid+Disease 数据集选取若干条数据，对基于矩阵约简的Apriori 改进算法进行实例分析，通过数据预处理获得适合数据挖掘格式要求的目标数据，数据库如表1 所示，TID 为Thyroid+Disease 的分类，ITEM SET 为Thyroid+Disease 属性信息，设最小支持度为0.3。

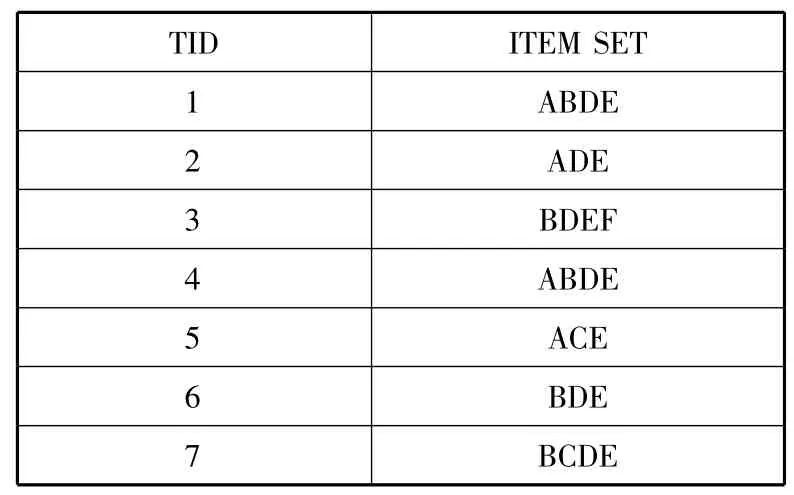
表1 Thyroid+Disease 分类明细

1)构造事物矩阵R，计算每个项集的支持数及项目个数，按照支持项目数对其进行降序排序，如下所示。

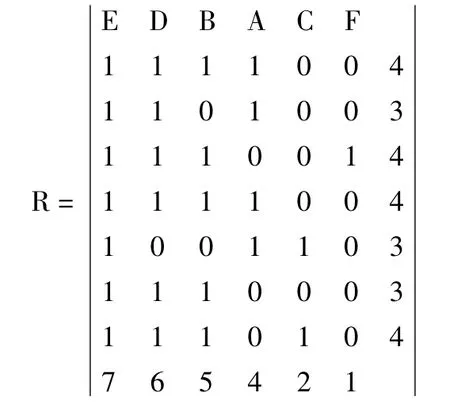
计算最小支持数为:

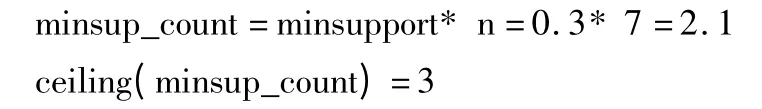
则最小支持数为3。

2)根据矩阵R 求频繁1-项集，重新布置矩阵R1。

由矩阵R 知，项F，C 的支持数为1、2 均小于最小支持数3，所以为非频繁集。删除第1 列和第2 列得到矩阵R1，如下所示。

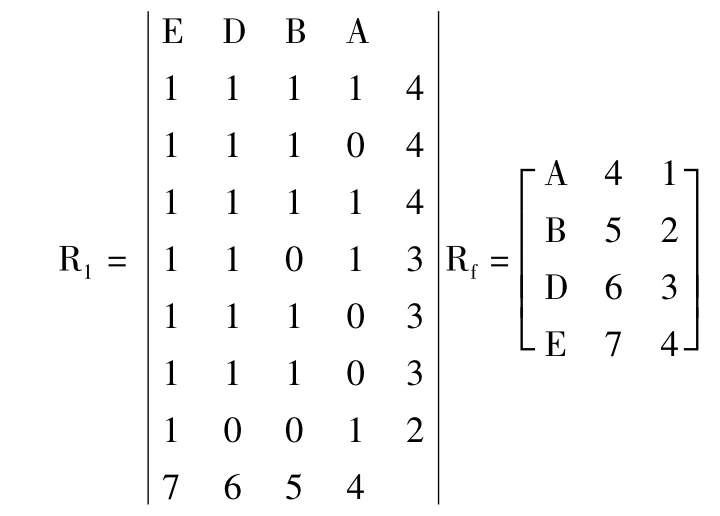
由矩阵得出频繁1-项集为L1={{A}，{B}，{D}，{E}}。

3)根据矩阵R1求频繁2-项集。

根据定理1 得到矩阵R2。

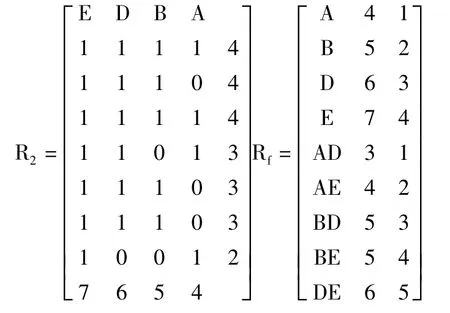
分别选取A 和D 进行与运算:

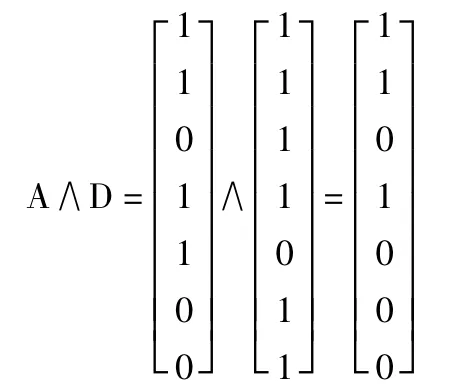
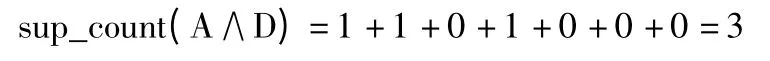
sup_count(A∧D)=minsup_count=3，所以频繁{A，D}为频繁2-项集，存储在L2中。根据上述计算步骤算出其它候选项集，得到L2={{AD}，{AE}，{BD}，{BE}，{DE}}。

4)利用3)的流程，求取3-频繁项集。

根据定理1 得到矩阵R2。

则余下的项组合 C3={{ABD}，{ABE}，{ADE}，{BDE}}，并进行与运算求出各个组合的支持数:count(ABE)=2，count(ADE)=3，count(ABD)=2，count(BDE)=5，由此看出只有{ADE}和{BDE}的支持数大于最小支持数，所以频繁3-项集为:L3{{ADE}，{BDE}}。根据定理3 可知频繁3-项集为此数据集的最大频繁集。由辅助矩阵Rf得出频繁项集:L=L1∪L2∪L3。由此证明了算法的可行性。

3.2 挖掘结果分析

为了验证改进算法的执行效率，在Intel(R)Core(TM)2 Duo CPU，内存为2 GB，系统为Windows7 的计算机上，用C#语言实现基于矩阵约简的Apriori 改进算法和传统的Apriori 算法，数据来自UCI 数据集中的Thyroid+Disease 样本数据集(http://archive.ics.uci.edu/ml/datasets/Thyroid+Disease)，该数据库中含有7 200 记条数据，连同一个22 个属性类别，在实验进行前对数据进行预处理，使其符合算法对数据的要求。做如下2 个实验:

实验1 在不同最小支持度的情况下对这2 种算法进行执行效率比较，结果如图1 所示，横坐标为支持度，纵坐标为时间(s)。在相同最小支持度的条件下，基于矩阵约简的Apriori 改进算法所用的时间明显较少，在支持度较小时改进的Apriori 算法处理效率更高。

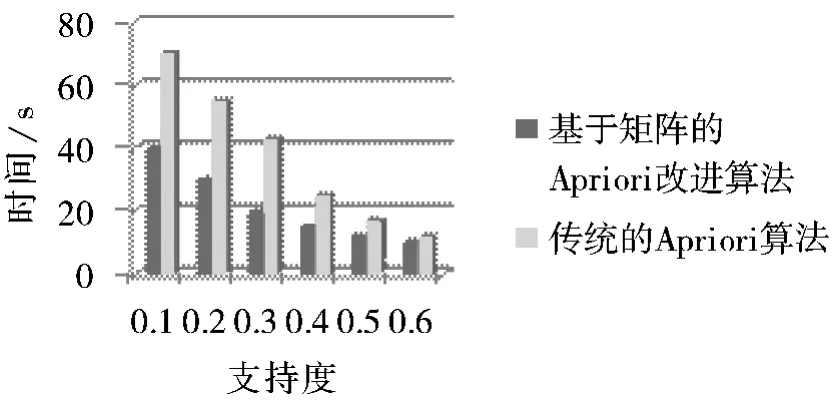
图1 改进的Apriori 算法与原Apriori 算法在执行时间上的对比

实验2 在不同最小支持度的情况下对这2 种算法进行生成频繁项集个数的比较，结果如图2 所示，横坐标为支持度，纵坐标为频繁项集的个数。在相同最小支持度的条件下，随着最小支持度的增加基于矩阵约简的Apriori 改进算法所生成的频繁项集个数与传统Apriori 算法的频繁项集个数趋近相等。

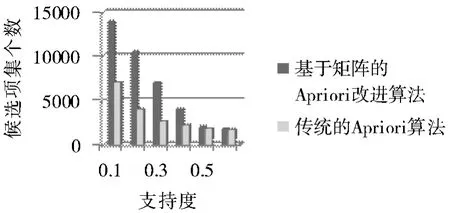
图2 改进的Apriori 算法与传统的Apriori 算法在生成候选项集个数上的对比

传统的Apriori 算法的执行效率与算法生成的候选项集个数和扫描数据库次数密切相关，改进的Apriori 算法很好地降低了这2 个指标，执行效率大幅度提高。

4 结束语

基于矩阵约简的Apriori 改进算法只需扫描事物数据库一次，有效地避免了相同候选集的生成，随着k-项集的k 值增加，矩阵变得越来越简单，求候选k-项集的支持数的时间也就越少;该算法将对数据库的扫描转换成对内存的扫描，大大提高挖掘关联规则算法的执行效率。综上所述，基于矩阵约简的Apriori改进算法克服了传统的Apriori 算法重复多遍扫描数据库的缺陷，节约了系统资源，提高了算法执行效率。

［1］孟祥萍，钱进，刘大有.基于数组的关联规则挖掘算法［J］.计算机工程，2003，29(15):98-99，109.

［2］张文东，刘新恩.一种基于向量的关联规则挖掘算法改进［J］.微计算机应用，2009，30(2):74-75.

［3］张忠平，李岩，杨静.基于矩阵的频繁项集挖掘算法［J］.计算机工程，2009，35(1):84-85.

［4］许晓东，李柯，朱士瑞.Web 使用挖掘中Apriori 算法的改进研究［J］.计算机工程与设计，2010，31(3):539-541.

［5］孙逢啸，倪世宏，谢川.一种基于矩阵的Apriori 改进算法［J］.计算机仿真，2013，30(83):245-249.

［6］黄治国，王淼.基于决策矩阵的可信关联规则挖掘方法［J］.计算机工程与设计，2014，35(8):2890-2895.

［7］苗苗苗，王玉英.基于矩阵压缩的Apriori 算法改进的研究［J］.计算机工程与应用，2014，49(1):159-162.

［8］Han Jiawei，Kamber Micheline.数据挖掘:概念与技术［M］.北京:机械工业出版社，2001.

［9］刘敏娴，马强，宁以风.基于频繁矩阵的Apriori 算法改进［J］.计算机工程与设计，2012，33(11):4235-4239.

［10］胡维华，冯伟.基于分解事务矩阵的关联规则挖掘算法［J］.计算机应用，2014，34(S2):113-116.

［11］罗森林，马俊，潘丽敏.数据挖掘理论与技术［M］.北京:电子工业出版社，2013:16-19.

［12］崔贯勋，李梁.关联规则挖掘中Apriori 算法的研究与改进［J］.计算机应用，2010，30(11):2952-2955.