基于量子信号处理的数字半色调算法

席 亮

(1.上海市普陀区业余大学信息工程系，上海 200062;2.上海开放大学普陀分校信息工程系，上海 200062)

0 引言

数字半色调技术是指把连续色调图像通过计算机程序转化成二值图像的方法［1］。由于目前大部分图像输出设备都是以二值图像的形式输出，因此数字半色调技术在打印、显示、纺织、印刷、传真、激光雕刻等领域得到了广泛应用［2-4］。半色调算法的优劣直接影响到输出图像的质量，实现半色调技术的关键是使生成图像中像素点的分布最优化，在视觉效果上尽可能地接近原始连续色调图像。

目前半色调的研究主要集中在抖动法、误差扩散法和迭代法3 种［5］。

1)抖动法的典型代表是利用bayer 设计的抖动矩阵与原图进行比较产生半色调图像，该方法将产生大量人眼能够辨别的人工纹理，并且细节丢失严重。

2)误差扩散算法把二值图像与原图像素值之差按一定比例分散到还未处理的其他像素上，因而具有自我校正能力，得到的半色调图像效果较好，但也会出现结构性纹理，且边缘模糊。许多学者对此进行了改进，Ostromoukhov 提出了快速误差扩散算法［6］，叶玉芬等提出了基于视觉差的误差扩散算法(PEBED)［7］等，但都无法完全消除纹理现象。

3)迭代法先用一种简单半色调算法得到二值图像，然后反复进行迭代处理，使每次得到的图像与原图相比误差更小，直到生成最优半色调图像。例如基于人类视觉模型(HVS)的DBS 算法和Pang 等以结构相似度(SSIM)模型为基础提出的SAH 算法［8］。迭代法虽然生成的半色调图像效果最好，但计算复杂度较高，很难用于实时处理场合。

近年来，基于量子力学理论的信息处理技术受到了学者们的极大关注，量子神经网络、量子遗传、量子粒子群优化等方面的研究成果层出不穷［9-10］。2001年Eldar 等首次引入了量子信号处理(QSP)概念［11］，提出了QSP 基本框架。2003 年Tseng 等基于QSP 框架首次提出了量子数字图像处理的方法［12］。在国内，谢可夫教授提出了一种数字图像量子比特表示的统一形式［13］，并推导出量子衍生图像边缘检测［14］、基于量子理论的自适应中值滤波［15］等算法。付晓薇把量子概率统计的理论成功应用于医学图像的增强［16］，本文作者提出了一种基于量子衍生图像分解的图像融合方法［17］。

本文结合上述研究成果，提出一种基于量子信号理论的数字半色调算法，通过仿真实验表明该方法较之传统的半色调算法具有更好的视觉效果。

1 量子信号理论基本概念

1.1 量子比特

经典计算机使用比特(bit)作为信息存储的基本单元，用0 和1 表示2 种不同的状态，量子力学理论中也有一个类似的概念——量子比特(qubit)，量子信息理论是建立在量子比特基础上。类似于经典比特的2 个基本状态0 和1，量子比特也有2 个基态|0〉和|1〉，但量子比特是由2 个基态的线性叠加构成的双态量子系统。在量子力学中，这2 个基态可以分别对应电子的自旋向上方向或自旋向下方向，也可以对应光子的垂直偏振方向或水平偏振方向。量子比特可用如下方式来表示:

其中，a 和b 是2 个复系数，分别表示状态|0〉和|1〉的概率幅，并且它们满足归一化条件|a|2+|b|2=1，另外|a|2和|b|2分别表示2 个基态|0〉和|1〉出现的概率［18］。显然，当a=0 或b=0 时，量子比特退化到经典比特0 或1 的形式，因此可以认为经典比特是量子比特的特例。

在量子世界中，微观粒子的状态是不确定的，它可以不同概率处于多个不同的状态，但一旦经过量子测量后，将坍缩到一个确定的状态。量子比特不仅可以表示，2 个基态|0〉和|1〉，还可以表示|0〉和|1〉之间所有可能的连续状态，但经过测量会坍缩到基态|0〉或|1〉。

1.2 量子信号处理框架

美国麻省理工学院的Eldar 等人在2001 年首次提出了量子信号处理(QSP)的概念。QSP 是基于量子力学的基本理论和数学体系建立，在经典计算机上实现新的或改进的信号处理算法的框架。它不依赖于量子物理设备，不受量子系统的物理约束，可以充分发挥量子力学理论数学体系的优势，是量子衍生方法在信号处理领域应用的理论基础。QSP 是一种信号处理新算法的生成机制，为信号处理理论提供了一种新的思路，这一思路与神经网络、遗传算法相似，也是一种对自然现象仿真的算法框架。

QSP 框架对现有算法进行改进的过程包括3 个步骤，输入映射、QSP 测量和输出映射，如图1 所示。

图1 量子信号处理框架

1)将待处理的输入信号表示成量子比特的形式，即量子叠加态;

2)将现有信号处理算法表示成对量子态的测量，通过设计不同形式的测量算子和修改测量算子中的参数来改进已有的算法或生成新的算法，并充分利用量子系统数学框架的形式使其在经典计算机上得以实现;

3)将对量子态进行测量的结果转化成为信号原来的表示形式并输出。

目前大部分信号处理算法都可以利用QSP 框架抽象成为由输入信号通过相应处理得到符合要求输出的模式。图像处理是信号处理的一个重要分支，QSP 框架在图像处理领域必能得到有效应用，但目前国内外相关研究还比较少。

2 量子半色调算法

本文基于Eldar 等提出的QSP 框架，对传统数字半色调算法中的误差扩散算法进行改进，提出一种基于量子信号处理理论的数字半色调方法。

2.1 生成二值图像

假设f(m，n)为一幅经过归一化的灰度图像，f(m，n)∈［0，1］，首先将图像f(m，n)中的每一个像素值都转化成如下所示的量子比特形式:

其中，|a|2和|b|2分别是该量子比特经测量后出现基态|0〉和|1〉的概率，并且满足|a|2+|b|2=1。|a|2和|b|2的计算可以采用以下方法。

在传统误差扩散算法中半色调图像某一点的像素值取决于该点原始像素值和相邻已处理过的像素点的误差值，如图2 所示。

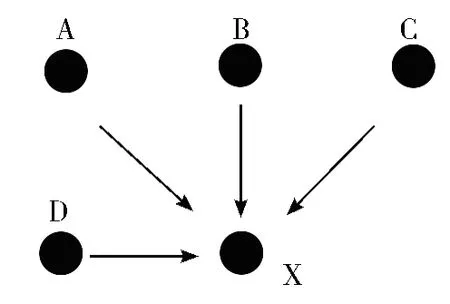
图2 误差扩散示意图

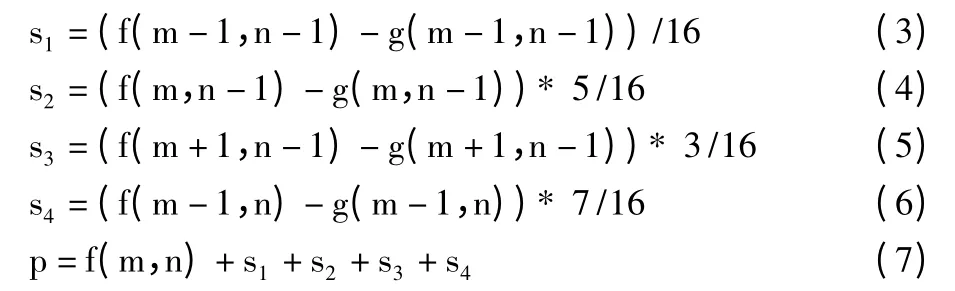
其中，s1～s4是已处理过的相邻像素点扩散到该点的误差值，g(m，n)是对应的二值图像。通过以下公式计算|a|2和|b|2:

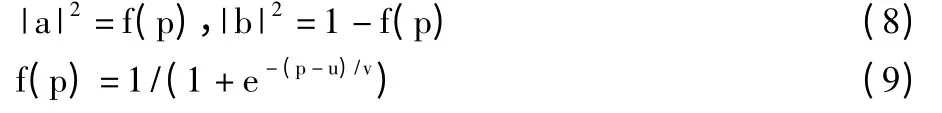
其中，f(p)为概率分布函数，参数u，v 为［0，1］之间的实数，经实验测试取u=0.1，v=0.01。

根据量子测量理论，量子比特|q(m，n)〉经过测量后将会以|a|2的概率坍缩成状态|0〉，以|b|2的概率坍缩成状态|1〉，从数字图像的角度看，可以认为坍缩成一幅二值图像，状态|0〉对应像素值0，状态|1〉对应像素值1。本文使用随机观测［10，12-13］的方式，对每一个量子比特进行随机测量，这种随机观测的方法虽然会产生一定程度上的不确定性，但经大量实验证明，这种不确定性只存在于很小的范围内，不影响定性分析。具体测量方法为:针对每一个量子比特|q(m，n)〉分别生成一个［0，1］范围内的随机数r，如果r∈［0，|a|2］则该量子比特坍缩到基态|1〉，对应二值图像的像素值为1，如果r∈(|a|2，1］则坍缩到基态|0〉，对应二值图像的像素值为0。由此灰度图像f(m，n)坍缩成了一幅二值图像g(m，n)。该二值图像与原图的误差为e(m，n)，e(m，n)=|f(m，n)-g(m，n)|。

2.2 误差反馈

半色调技术是用二值图像代替连续色调图像，因此处理后必将丢失一部分灰度信息，传统误差扩散算法虽然把误差传递到了周围像素，大幅减少了丢失的灰度信息，但也因此引入了人眼可见的结构性纹理，并且导致边缘模糊，过渡不连续，图像对比度降低等问题。因此，本文引入误差反馈机制，将二值图像g(m，n)与原始图像f(m，n)的误差e(m，n)乘以自适应反馈系数后对原图进行增强处理。反馈原则为对于较亮区域进行正反馈，使其亮度增加，灰度值趋近于1，对于较暗区域进行负反馈，降低其亮度，使其灰度值趋近于0，对增强过的图像再进行传统误差扩散处理得到的半色调图像将具有更高的对比度，并且能够减少结构性纹理现象。同时这种自适应误差反馈机制也可以把上文中量子随机观测带来的不确定性进一步降低。

设自适应反馈系数为H，表示误差e(m，n)对原图的影响程度，f'(m，n)为增强后的图像，反馈方程为:

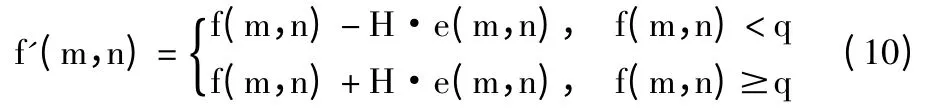
其中，q 是一个常量，可用来调节图像增强的效果，取q=0.196。反馈系数H 的计算借鉴文献［7］中的方法，使用以下公式:

其中，favg(m，n)为当前像素点及附近八邻域的像素均值，即:

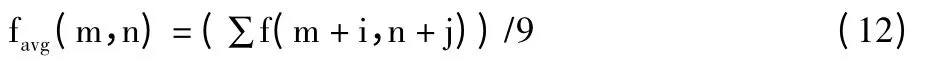
其中，-1 ≤i ≤1，-1 ≤j ≤1。

2.3 算法实现

本算法的具体实现过程包括以下几个步骤:

1)利用公式(3)～公式(9)计算|a|2和|b|2，把归一化后的灰度图像f(m，n)中的每个像素点表示成量子比特的形式。

2)对每一位量子比特分别生成一个［0，1］范围内的随机数，对其进行随机测量，利用量子坍缩原理得到二值图像g(m，n)，并计算该图像与原图的误差e(m，n)。

3)利用公式(11)计算自适应反馈系数H。

4)利用公式(10)对原图的每一个像素进行增强处理，得到新的连续调图像f'(m，n)。

5)对f'(m，n)按照传统误差扩散算法进行处理得到最终的半色调图像。

3 仿真实验及性能评价

3.1 仿真实验的主观评价

为了验证算法的有效性，本文选择了数字图像处理中常见的3 幅图像作为仿真实验对象，3 幅图像lean、peppers、barbara，均为8 bit 灰度图像，大小为512 ×512。仿真实验结果分别如图3～图5 所示。其中，子图(a)为原始图像，子图(b)为采用bayer 抖动矩阵得到的半色调图像，子图(c)为使用Floyd-Steinberg 滤波器的传统误差扩散算法得到的半色调图像，子图(d)、(e)分别是文献［19-20］中提出的算法得到的结果，子图(f)为本方法得到的半色调图像。虽然本文使用的量子随机测量导致最终产生的图像存在一定程度上的不确定性，但经实验测试，这种不确定性产生的差异肉眼很难直接察觉，故本文随机抽取了其中一幅半色调图像用来对比。图6 是使用本方法对lena 图片处理得到半色调图像的直方图，显然这是一幅二值图像，其余实验结果的直方图与此类似。

图3 图片lena 实验结果图

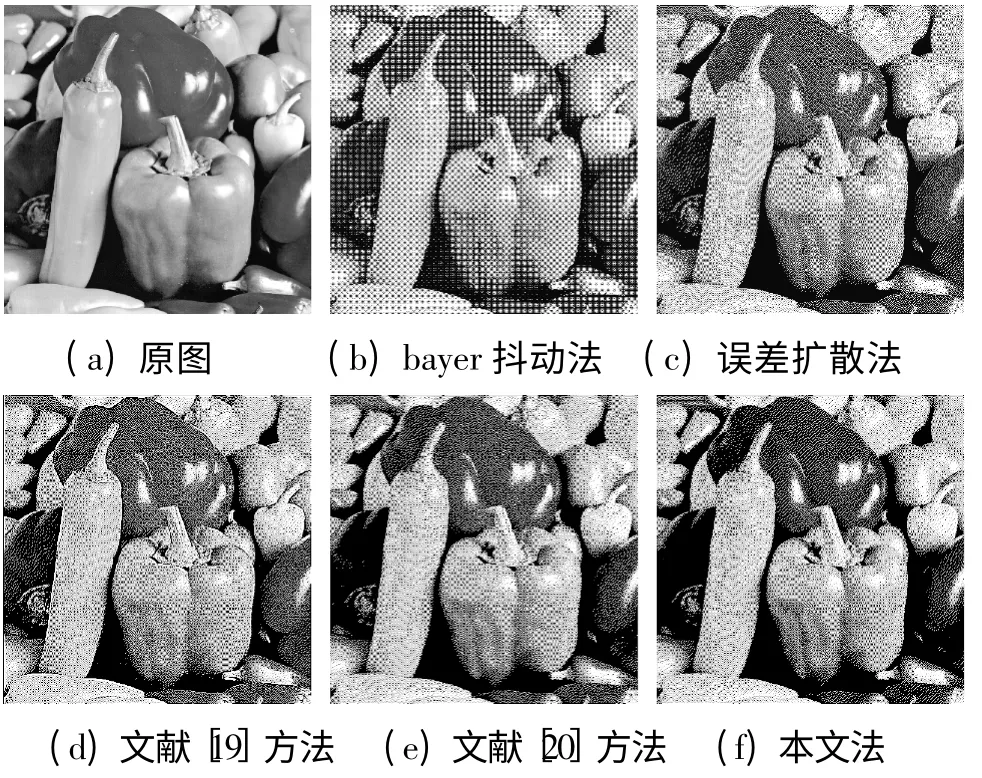
图4 图片peppers 实验结果图

图5 图片barbara 实验结果图

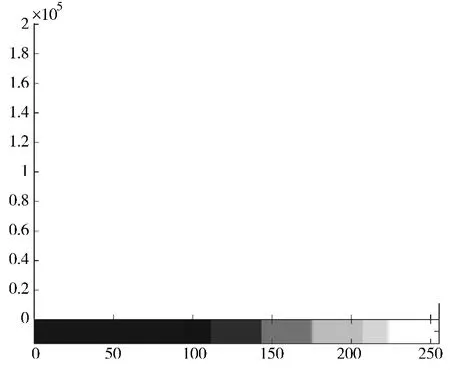
图6 本方法实验结果直方图(lena 图)

从3 组实验结果的主观感受分析，使用bayer 抖动矩阵得到的半色调图像比较模糊，点增益现象明显，使用传统误差扩散算法得到的结果清晰度较好，但有明显的人工纹理现象，且边缘过渡模糊，文献［19］提出方法的结果边缘特征明显，但人工纹理现象仍然严重，文献［20］提出的方法人工纹理现象得到大幅减少，本方法得到的半色调图像与文献［20］的结果比较接近，但人工纹理现象得到进一步减少，尤其黑色区域几乎没有纹理，并且图像对比度更高，整体视觉效果更好。

3.2 仿真实验的客观评价

由于人的主观评价容易受到情绪、环境、性格等影响，评价尺度很难把握，因此本文同时采用以下客观指标作为评价依据:

1)峰值信噪比(PSNR)。

峰值信噪比是指图像峰值信号能量与信号噪声方差的比值。该值主要反映图像亮度的相似性和噪声水平。PSNR 值越大说明半色调图像的质量与原图越接近，具体计算公式如下:

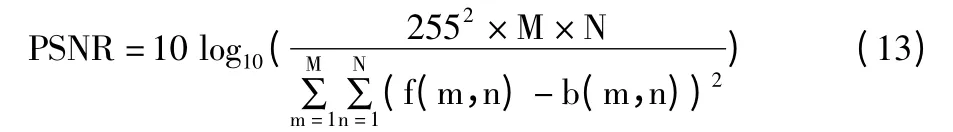
其中，M 和N 为图像的行数和列数，f(m，n)和b(m，n)分别为原始图像和半色调图像的灰度值。

2)归一化均方误差(NMSE)。

归一化均方误差的计算方法为半色调图像与原图对应像素灰度值之差的平方和，与原图所有像素灰度值平方和的比值。该评价指标能够在一定程度上反映出2 幅图像之间的相似程度。NMSE 值越小，说明半色调图像与原始图像整体上越接近。具体计算公式为:

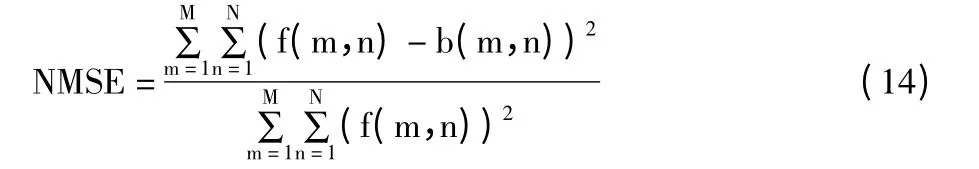
3)结构相似度(SSIM)。

结构相似度指标根据人眼的视觉特点，把亮度、对比度和结构3 个指标构成一个相似度系统来评价2 幅图像的相似程度［21］。具体计算公式为:

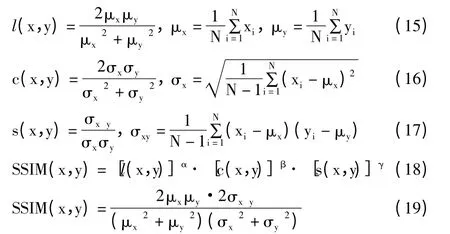
其中，l(x，y)，c(x，y)，s(x，y)分别为亮度、对比度和结构信息函数，α，β，γ 均为正数，用来调节三者的权重，一般取α=β=γ=1。通常SSIM 的取值范围在［0，1］之间，SSIM 值越大表明2 幅图像的相似度越高，差异越小。

对lean、peppers、barbara 3 幅图片分别使用bayer抖动法、传统误差扩散法、文献［19］和文献［20］提出方法和本方法计算上述3 个评价指标值。考虑到本方法在量子随机观测时会产生一定程度的不确定性，仿真实验时对此进行了大量测试，表1 中的数据是lena 图片经过10 次实验后的3 个客观评价指标值。从表中可以看出，这种不确定性带来的差异在客观评价指标上只体现在小数点后第3 位，不影响对其进行客观评价，故本文随机抽取其中一组数据与其他算法进行对比。

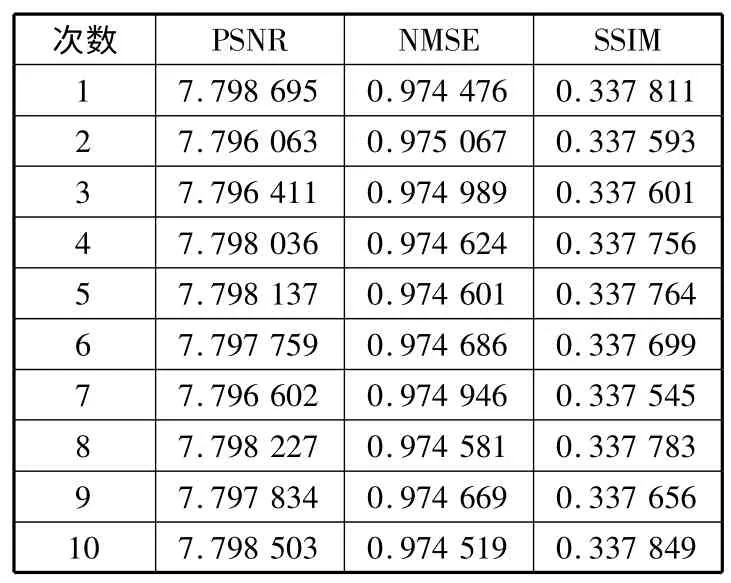
表1 本方法10 次实验结果对比表(lena 图)

表2～表4 中的数据是对3 幅实验图片分别使用本方法等5 种方法计算得到的客观评价指标值。

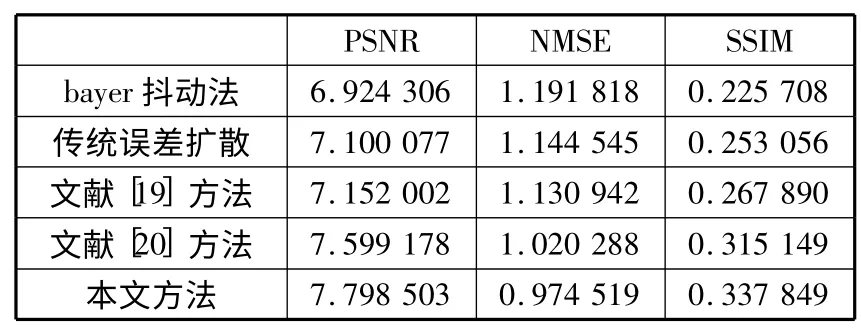
表2 图片lena 实验结果对比表

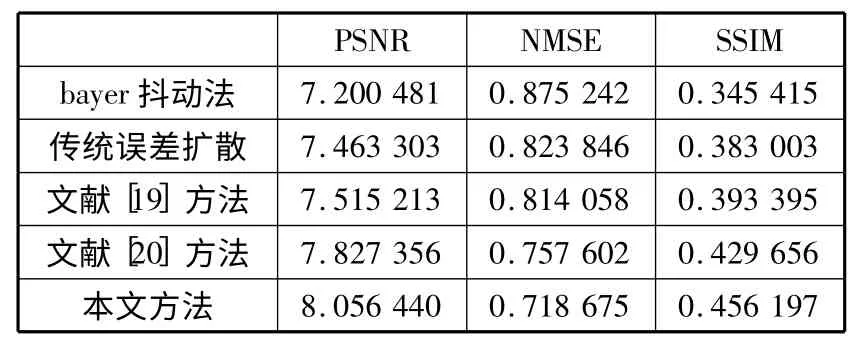
表3 图片peppers 实验结果对比表

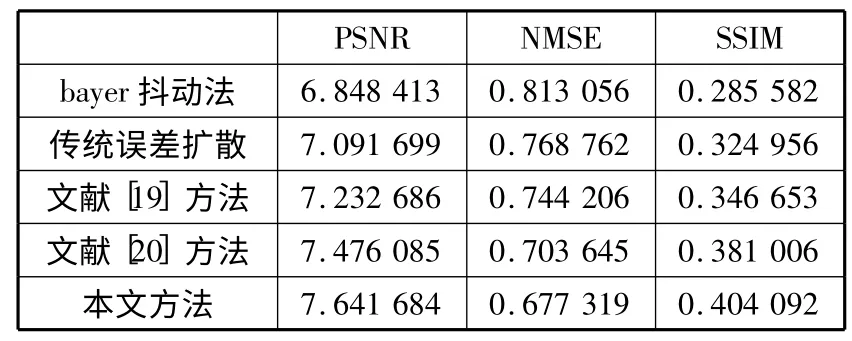
表4 图片barbara 实验结果对比表

从3 张表中的实验数据可以看出，使用本方法得到的半色调图像PSNR 值和SSIM 值最大，NMSE 值最小，说明它与原图最接近，相似度最高，差异最小。因此从客观评价指标上分析，本文提出的方法也优于其他几种方法。

4 结束语

本文基于量子信号理论和传统的误差扩散算法，提出了一种新的数字半色调方法，通过仿真实验表明使用该方法得到的半色调图像效果较好，主、客观评价均优于传统的半色调算法。该方法为研究数字半色调技术提出了一种新的思路，但视觉效果上相比迭代法的仍有一定差距，后续研究将结合迭代法对其进行进一步优化，以期获得更好的视觉效果，同时降低迭代法计算的复杂度。此外进一步降低量子随机观测带来的不确定性，或使用更好的量子测量方法也是今后进一步研究的方向。

［1］徐国梁，谭庆平.图像半色调化算法研究综述［J］.计算机工程与科学，2012，34(12):87-97.

［2］冯起芹，曹小龙，单武扬，等.印刷品水印图像的半色调算法比较［J］.包装学报，2012，4(3):34-38.

［3］陈若愚.AM-OLED 图像数字半色调算法研究［D］.武汉:华中科技大学，2011.

［4］徐向超，薛伟.模糊滤波误差扩散半色调技术在激光雕刻领域的应用［J］.山西科技，2014，29(3):45-47.

［5］史琳.数字半色调技术研究［D］.西安:西安电子科技大学，2007.

［6］Ostromoukhov V.A simple and efficient error diffusion algorithm［C］// Proceedings of the ACM SIGGRAPH Conference on Computer Graphics.2001:567-572.

［7］叶玉芬.数字半色调技术中的误差扩散算法研究［D］.西安:西安电子科技大学，2006.

［8］Pang W M，Qu Y，Wong T T，et al.Structure-aware halftoning［J］.ACM Transactions on Graphics，2008，27(3):89-97.

［9］Purushothaman G，Karayiannis N B.Quantum Neural Networks(QNNs):Inherently fuzzy feedforward neural networks［J］.IEEE Transactions on Neural Networks，1997，8(3):679-693.

［10］Han K H，Kim J H.Quantum-inspired evolutionary algorithm for a class of combinatiorial optimization［J］.IEEE Transactions on Evolutionary Computation，2002，6(6):580-593.

［11］Eldar Y C，Oppenheim A V.Quantum signal processing［J］.IEEE Signal Processing Magazine，2002，19(6):12-32.

［12］Tseng C C，Hwang T M.Quantum digital image processing algorithms［C］// The 16th IPPR Conference on Computer Vision Graphics and Image Processing.2003:827-834.

［13］谢可夫.量子衍生图像处理方法的研究［D］.长沙:中南大学，2007.

［14］谢可夫，许悟生.量子衍生图像分解和边缘检测［J］.计算机应用，2013，33(4):1089-1091.

［15］谢可夫，许悟生.基于量子理论的图像中值滤波［J］.计算机工程，2013，39(1):244-247.

［16］付晓薇，丁明跃，周成平，等.基于量子概率统计的医学图像增强算法研究［J］.电子学报，2010，38(7):1590-1596.

［17］席亮.基于量子力学和拉普拉斯金字塔的图像融合方法［J］.计算机与现代化，2015(4):37-41.

［18］Nielson M A，Chuang I L.量子计算和量子信息(一)［M］.赵千川译.北京:清华大学出版社，2004:13-14.

［19］梁永峰.一种改进的误差扩散算法［D］.西安:西安电子科技大学，2013.

［20］叶玉芬，郭宝龙，马佳.自适应反馈视觉感知差的误差扩散半色调算法［J］.微电子学与计算机，2006，23(6):155-159.

［21］姚莉.数字半色调技术及其评价方法研究［J］.计算机工程与应用，2010，46(3):4-8.