改进的ISOMAP 算法在人脸识别中的应用

郭海凤，陈月霞，孙周宝

(1.金陵科技学院信息技术学院，江苏 南京 211169;2.河海大学计算机与信息学院，江苏 南京 210098)

0 引言

随着互联网技术的飞速发展，其蕴含的图片数量呈爆炸式的增长，而绝大部分的图像没有任何的标签类别信息，而且图像检索所面临的主要难题是“语义鸿沟”，即低层图像特征与高层用户语义间的巨大差异，从而使得图像检索的效果很难让用户满意。目前图像检索的方法主要是基于内容的图像检索。

在图像检索过程中，一幅大小为64 ×64 的人脸图像在空间中需要用4096 维的向量进行表示，显而易见的是这个向量太大，导致任何算法在处理时都非常困难，为了避免维数灾难问题，需要对图像进行降维处理。传统的降维方法包括主成分分析(PCA)［1］、独立分量分析(ICA)［2］以及多尺度变化(MDS)［3］等，从几何学角度来看，这些线性的降维方法首先都假设数据具有全局的线性结构，而人脸图像的集合可以看作是以位置、姿态、光照等为参数的一个高维数据空间，当人脸在表情和姿态有变化的时候会带来很多非线性变形，其相应的特征变化可看作嵌入在高维人脸图像空间中的一个低维非线性子流形，这时传统的降维方法则无法揭示非线性高维数据的内在本质结构。流形是一种非欧几何空间，用已知的局部逼近未知的全局几何结构，目的是在流形空间结构下挖掘非线性高维数据的内在结构及规律。所以流形学习技术能够真正地揭示人脸图像空间的内在低维结构，可以有效地用来对人脸图像进行识别。目前，应用比较广泛的流形学习方法包括ISOMAP(Isometric Mapping)［4-5］、LLE (Locally Linear Embedding)［6-14］以及LE(Laplacian Eigenmap)［15］等。相比传统的降维方法，流形学习方法具有很多优势:参数较少，只有近邻参数k 及内在维数估计参数d;其次是计算性能对数据的非线性流形结构具有一定的自适应性。

人脸图像的识别主要包括特征提取和人脸识别2 部分。

1)特征提取主要是抽取出具有最大像素分类特征的像素点，从而降低人脸识别过程的复杂度;

2)人脸识别主要是利用提取的特征及人脸信息进行比较，采用分类算法进行分类，达到识别的目的。

本文结合特征提取算法SIFT［16-17］及改进的流形学习方法ISOMAP，在ORL 标准人脸数据集上进行人脸识别实验。利用SIFT 算法提取人脸图像的局部描述子，在获取每张人脸图像的128 维高维特征向量后，使用改进的ISOMAP 算法进行降维，并使用最近邻分类器分类。本文在使用ISOMAP 算法过程中，主要分析探讨近邻参数以及内在本征维数的大小对人脸图像识别效果的问题。

1 SIFT 与ISOMAP 算法

1.1 SIFT 概述

SIFT 特征是哥伦比亚大学的David Lower 于1999 年提出的局部特征描述子，2004 年David Lower又对SIFT 进行更深层次的研究和扩展，SIFT 分辨力强，信息量大，具有很好的仿射不变性。SIFT 基本思想是通过高斯核进行滤波提取图像的尺度空间中的稳定点。这种方式获得的特征点具有旋转、缩放、平移和部分仿射不变性，进一步将特征向量的长度归一化。SIFT 特征提取算法用于人脸识别时，相似的人脸的SIFT 特征是比较接近的，不相似的人脸其特征则差别较大。SIFT 特征是图像的局部特征，描述的是图像关键区域的梯度直方图分布情况，SIFT 算法的实质是从人脸图像中提取SIFT 关键点(keypoints)的过程，算法包括4 个主要的步骤:

1)尺度空间的构建与极值检测;

2)特征点精确定位;

3)特征点主方向确定;

4)SIFT 描述子生成。

具体过程参见文献［7-8］。针对ORL 人脸图像中最后一个人的数据集，使用SIFT 算法，在其中2 张图像上生成的关键点和描述子及匹配情况如图1 所示。

图1 关键点及匹配情况

1.2 ISOMAP 算法

ISOMAP 算法是利用局部近邻距离对全局流形测地线距离进行估计，通过建立原数据的测地距离与降维数据空间距离的对等关系，实现数据降维。ISOMAP 算法可以挖掘出高维数据本质对应的低维嵌入结构，主要是因为其使用的测地距离能够内在地反映数据的本质流形几何特征。算法主要步骤如下:

1)运用ε-邻域或k 近邻方法对原始数据构建近邻图G;

2)计算任意节点对在近邻图G 中的最短路径，用来逼近相应的测地距离;

3)将步骤2)中获得的测地距离矩阵作为输入，应用MDS 算法计算数据的低维空间表示，将数据映射到低维可视空间中。

对于给定的人脸数据集，通过使用SIFT 特征提取算法获得高维的人脸特征向量后，ISOMAP 能否成功地降维取决于邻域大小k 的选择，以及人脸图像的内在维数d 的估计是否合适，因为只有合适的k 才可以保证对测地距离的计算及逼近，如果k 过大，则可能严重破坏原始流形的连通性;如果k 过小，则可能导致流形结构被划分成许多包含“孔洞”的不连通区域。在近邻因子k 的大小选取时，为了自适应确定最优邻域参数k，在可以有效保持拓扑结构不变的前提下，对于给定的邻域因子的范围k1，k2，…，ki，…，kn，计算每个 ki的映射损失函数 L (ki)=‖τ(DG)-τ(DY)‖2，取最小的L(ki)所对应的k 组成初始候选集合Z，对每个k∈Z，使用改进后的LLE算法并计算相应的误差，误差标准采用公式(1):

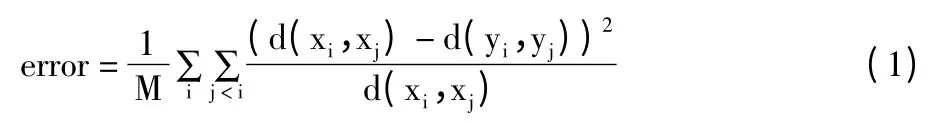
在内在维数d 的估计过程中，如果d 过小，则高维空间中的点在映射到低维空间中会有重叠等现象，从而导致数据不能正确识别;相反，则可能包含噪声数据在内的多余信息，为后续的识别造成不可估计的影响。本文采用向量的重构残差(1 -，其中ρ为测地距离矩阵DX(K)和低维空间中的欧式距离矩阵D(Y)的相关系数)以及最大似然估计2 种方法来估计内在维数的大小。通过建立近邻间距离的似然函数，得到本征维数的极大似然函数，从而得到最后的极大似然估计值。对人脸空间中的样本随机采样X1，X2，…，Xn，构造泊松分布:

对于给定的邻域k，则点xi的内在维数最大似然估计为:

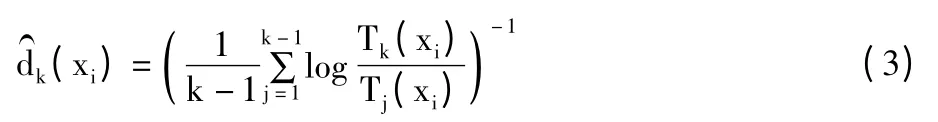
采用极大似然估计法对式(2)中的x 进行遍历，可得到n 个局部本征维数的估计值，然后取其平均值作为内在的嵌入维数，即:。最大似然估计法从人脸数据的局部结构性质出发，通过一定的描述方式来估计本征维数，并采用概率统计方法，可较好地估计数据的内在维数，计算速度也较快。

2 实验结果与分析

本文在ORL 人脸数据集上进行实验分析。该数据库共包含40 个人的400 张人脸图像，每人平均10张图像，尺寸为92 ×112 像素。这些人脸图像经过了中心化和标准化，由于该数据集不涉及到光照，所以人脸图像的变化主要是姿态和表情，图2 为数据集中某个人的人脸图像。因为不同的训练样本数对识别的结果有着重要的影响，所以本实验采用随机选取每个人10 张中的5 张作为训练样本，剩余5 张图像作为测试集。实验中，选择使用简单方便的最近邻分类器来判别特征提取算法的分类效果。实验环境为128 核的CPU，63 G 内存，实验平台为Matlab 7.1。

图2 部分ORL 人脸图像

2.1 特征提取

针对ORL 人脸图像数据集，本文首先通过SIFT算法对人脸图像进行特征提取。对于获得的128 维特征向量，使用流形学习中的等距映射算法ISOMAP进行降维，在200 张人脸测试数据集上进行测试，并且将该算法与直接使用ISOMAP 算法得到的结果进行比较，在降维过程中，嵌入的维数和近邻参数默认为10，测试结果如表1 所示。

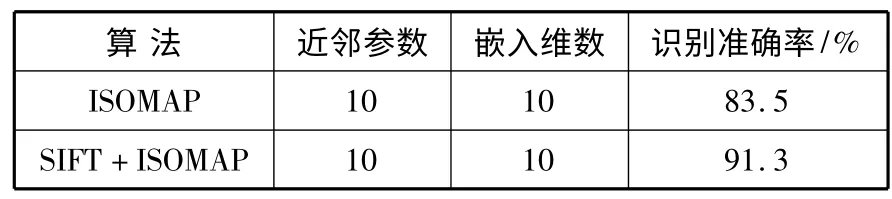
表1 ORL 人脸数据集上2 种算法比较

由表1 可以看出，在嵌入维数与构建近邻图时近邻参数设置相同的情况下，基于SIFT 算法提取的特征在使用ISOMAP 算法后具有更高的识别率，因为SIFT 算法在对人脸图像特征提取时，其仿射不变性发挥了重要的作用，可以有效提取描述人脸图像的关键点。

在相同的近邻参数及嵌入维数情况下，训练样本的个数不同对识别率有着一定的影响。对于2 种方法，实验中分别选取3 个、4 个、5 个、6 个、7 个、8 个样本作为训练集，剩余的7 个、6 个、5 个、4 个、3 个、2个作为测试样本，并且每次实验重复10 次取平均值作为识别结果，此时的近邻参数及嵌入维数仍设置为10，实验结果如图3 所示。

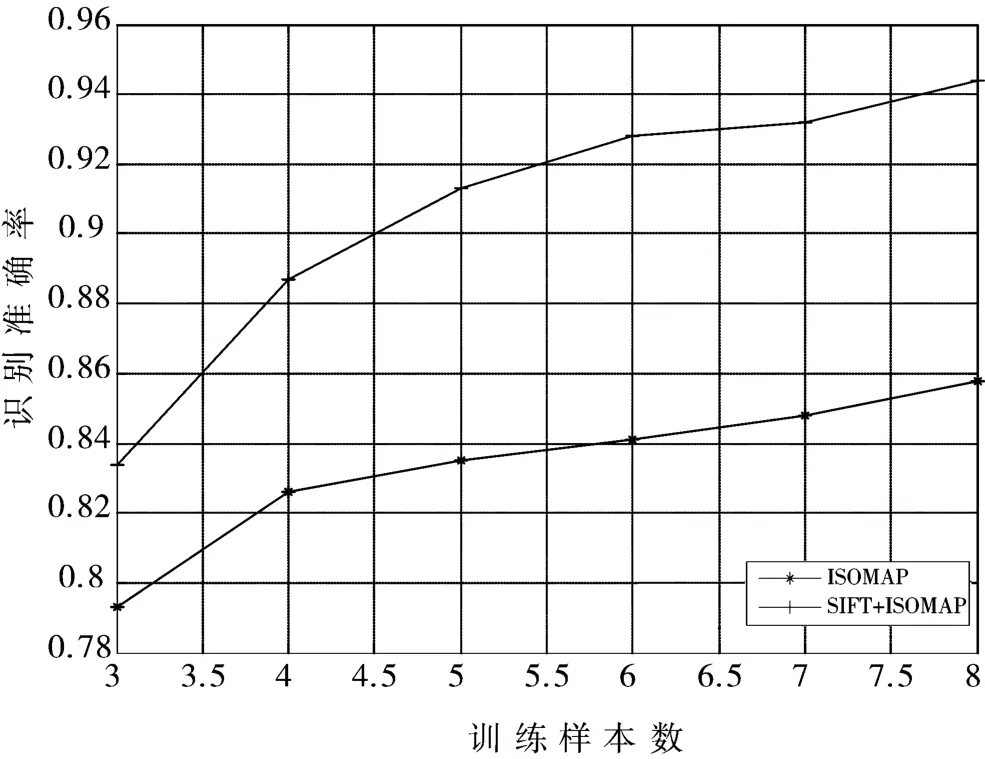
图3 识别率与训练样本数关系

2.2 近邻参数的选择

ISOMAP 算法是建立在局部线性假设的基础上，在计算低维流形结构时，其成功与否的关键在很大程度上取决于近邻参数的选择。在确定一个样本点线性近邻时通常包括2 个方面:测度距离和近邻参数的大小选择。在上述实验中，选择近邻参数为10，图4则为不同的近邻参数值对人脸图像数据的识别率的影响。

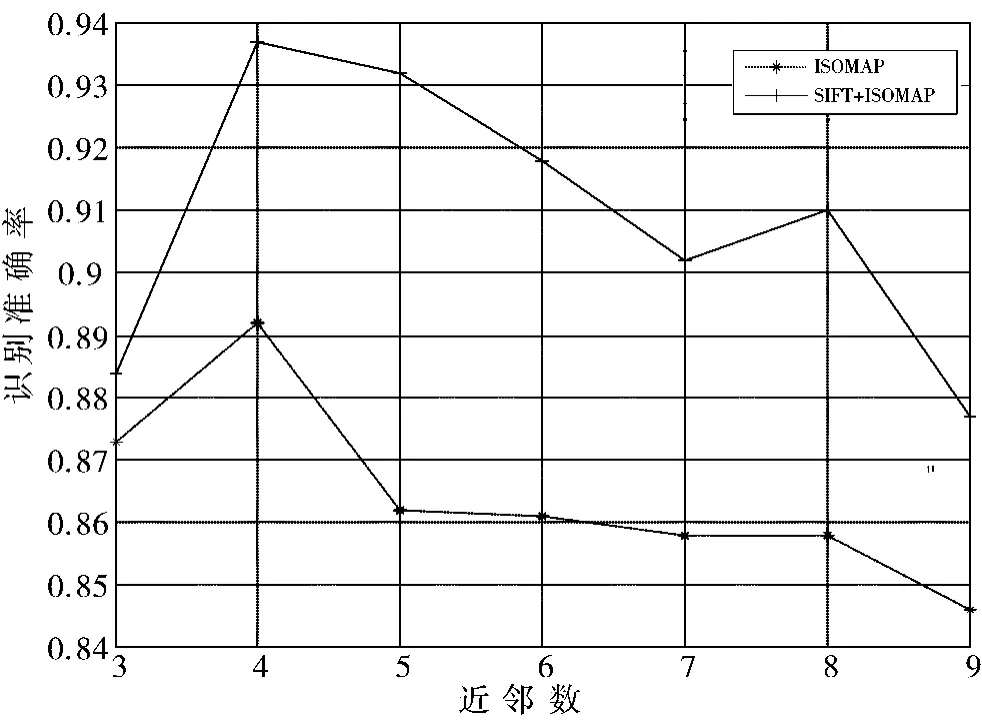
图4 识别率与近邻数关系

由图4 可知，近邻参数的大小选择对嵌入的结果有着很大影响。在固定嵌入维数(取值为10)时，算法在近邻值为5 时取得较好的识别效果。

2.3 嵌入维数的选择

样本数据的本征维数是嵌入在高位空间中低维流形的维数，本征维数的大小对低维空间的嵌入结果有着巨大的影响。因此，在流形降维的过程中需要解决高维数据的本征维数及嵌入到低维空间的维数的估计问题。在ORL 人脸图像上，本实验采用向量重构残差以及最大似然估计2 种方法进行维数的估计，实验结果如图5 所示。

图5 识别率、残差与嵌入维数关系

图5 对应的实验测试了该算法的识别率与嵌入维数、残差与嵌入维数的关系。本实验中固定近邻参数值设置为10。由图5(a)可知，在保持近邻数不变的情况下，随着嵌入维数的增加，识别率会逐步上升，但最后会趋于一个极限值附近，而ORL 人脸数据集在嵌入维数为10 时即可达到一个较高的识别率，图5(b)反映了嵌入维数估计时残差与维数之间的关系，可见ORL 人脸数据库的本征维数远比Swiss Roll或Yale 人脸数据集复杂，因为它包含了40 个人的不同姿态和表情人脸，这些与人们对人脸图像的理解也是一致的。

3 结束语

本文结合SIFT 特征提取算法与流形学习算法ISOMAP，在ORL 人脸图像数据集上进行图像检索实验。由实验可知，基于SIFT 算法提取的特征在使用ISOMAP 降维后具有更好的识别效果。在降维过程中，针对ISOMAP 算法依赖于近邻参数k 以及内在维数d 的大小难以选取的问题，本文使用最小残差及最大似然估计的方法来估计和选择近邻参数及内在维数的大小。由实验还可知，合适的近邻参数及内在维数对识别效果有着巨大的影响。

［1］Jolliffe I.Principal Component Analysis［M］.2nd ed.New York:Springer Verlag，2002.

［2］Comon Pierre.Independent component analysis:A new concept?［J］.Signal Processing，1994，36(3):287-314.

［3］Cox T F，Cox M A A.Multidimensional Scaling［M］.2nd ed.Chapman and Hall/CRC，2000.

［4］Tenenbaum J B，Silva V D，Langford J C.A global geometric framework for nonlinear dimensionality reduction［J］.Science，2000，290(5500):2319-2323.

［5］Tenenbaum J B.Mapping a manifold of perceptual observations［C］// Advances in Neural Information Processing Systems.1998，10:682-688.

［6］Wen Guihua，Jiang Lijun，Wen Jun.Kernel relative transformation with applications to enhancing locally linear embedding［C］// Proceedings of the International Joint Conference on Neural Networks.2008:3401-3406

［7］Roweis S T，Saul L K.Nonlinear dimensionality reduction by locally linear embedding［J］.Science，2001，2909(5500):2323-2326.

［8］Wang Heyong，Zheng Jie，Yao Zhengan，et al.Improved locally linear embedding through new distance computing［C］// Advances in Neural Networks.2006:1326-1333.

［9］Chang H，Yeung D.Robust locally linear embedding［J］.Pattern Recognition，2006，39(6):1053-1065.

［10］Valencia-Aguirre J，Álvarez-Mesa A，Daza-Santacoloma G，et al.Automatic choice of the number of nearest neighbors in locally linear embedding［C］// Progress in Pattern Recognition，Image Analysis，Computer Vision，and Applications.2009:77-84.

［11］Eftekhari A，Abrishami-Moghaddam H，Babaie-Zadeh M.k/K-Nearest neighborhood criterion for improvement of locally linear embedding［C］// Computer Analysis of Images and Patterns.2009:808-815.

［12］Goldberg Y，Ritov Y.LDR-LLE:LLE with low-dimensional neighborhood representation［C］// Advances in Visual Computing.2008:43-54.

［13］Zhang Shiqing.Enhanced supervised locally linear embedding［J］.Pattern Recognition Letters，2009，30(13):1208-1218.

［14］Hou Chenqing，Zhang Changhui，Wu Yi，et al.Stable local dimensionality reduction approaches［J］.Pattern Recognition，2009，42(9):2054-2066.

［15］Belkin M，Niyogi P.Laplacian eigenmaps for dimensionality reduction and data representation［J］.Neural Computation，2003，15(6):1373-1396.

［16］Lowe D G.Object recognition from local scale-invariant features［C］// Proceeding of IEEE International Conference on Computer Vision.1999，2:1150-1157.

［17］Lowe D G.Distinctive image features from scale-invariant keypoints［J］.International Journal of Computer Vision，2004，60(2):91-110.