CRTSⅠ型板式无砟轨道脱空状态对结构模态的影响

郭利康，张四放，杨荣山，赵坪锐，任娟娟

(西南交通大学高速铁路线路工程教育部重点实验室，成都 610031)

CRTSⅠ型板式无砟轨道脱空状态对结构模态的影响

郭利康，张四放，杨荣山，赵坪锐，任娟娟

(西南交通大学高速铁路线路工程教育部重点实验室，成都 610031)

以CRTSⅠ型板式无砟轨道作为研究对象，运用有限元软件ANSYS，建立有限元梁体模型，对轨道板不同脱空长度的轨道结构进行模态分析，为轨道结构的损伤识别提供理论指导。计算结果表明：随着轨道板脱空长度的增加，轨道结构的同阶固有频率减小；振型的波峰逐渐向脱空区域移动，在脱空区域轨道板的垂向位移增大，轨道板与凸台分离明显。

板式轨道；CA砂浆；脱空；模态分析；有限元

高速铁路的发展，对列车运行的安全性和舒适性提出了更高的要求。CRTSⅠ型板式无砟轨道作为客运专线高速铁路的主要轨道结构形式，为了满足轨道结构的高平顺性和高稳定性，对轨道结构的振动分析势在必行。CRTSⅠ型板式无砟轨道在长期服役过程中，它的振动形态会随着轨道结构状态变化而改变，扣件的性能、CA砂浆层的伤损和地基的沉降等都会对轨道结构的振动产生影响。采用模态分析理论研究CA砂浆层的伤损对CRTSⅠ型板式无砟轨道的振动特性的影响，建立有限元梁体模型，对CA砂浆层的不同伤损情况下的轨道结构进行模态计算，并进行振动分析。

1 模态分析简介

模态是多自由系统或连续体系统的一个固有属性，可由系统的特征值和特征向量表示。其中，固有频率就是系统特征值的平方根，系统的特征向量就是模态的振型。对于轨道结构，模态分析法就是利用模态振型矩阵的线性组合形式进行模态坐标变换，将其振动微分方程中的物理坐标变换成模态坐标，使方程解耦成为一组以模态坐标和模态参数描述的独立方程，可以像单自由度系统那样求出其模态响应，进而得到系统在物理坐标下的响应[1]。

轨道结构系统的振动方程为

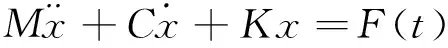
(1)

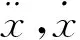
(2)

令x=φcosωt(φ为位移矢量的幅值)，并代入(2)可得

(3)

方程式(3)在任何时刻都成立，因此方程可以简化为

(4)

由线性代数可知，一个齐次线性方程组有非零解的充分必要条件是

(5)

2 有限元模型及参数

CRTSⅠ型板式无砟轨道主要由钢轨、WJ-7扣件、轨道板、凸台、CA砂浆层和底座板等组成[3]。

CA砂浆层的主要功能有施工调整、缓冲协调、提供少量的轨道竖向弹性等。CA砂浆层的伤损必然对轨道结构的振动产生影响，刘克飞等人基于车辆-板式轨道系统耦合动力学理论，研究了轨道板脱空(砂浆层伤损)对轨道结构振动响应的影响。其研究结果表明：随着轨道板脱空长度L的增大，当脱空长度L≤0.60～0.80m时，轮轨垂向力与减载率变化均很小，对行车安全影响较小；而当L≥0.60～0.80m时，最大轮轨垂向力呈明显增加的趋势，而最小轮轨垂向力明显减小，即减载率明显增大，表明行车安全性随之降低[4]。因此依据其研究结论，预设轨道板脱空长度分别为0、0.3、0.7和1.2m，通过模态分析轨道结构的固有频率和振型的变化。轨道板脱空示意见图1。

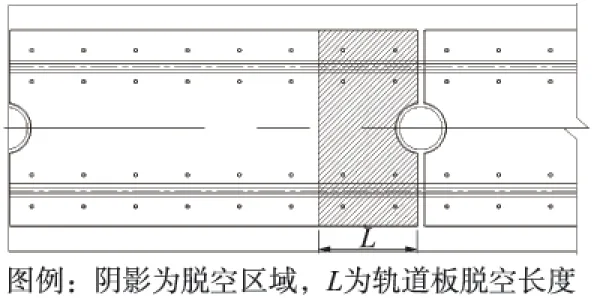
图1 轨道板脱空示意(俯视)

有限元模型共建立3块轨道板，这样能够有效地减弱边界效应的影响，更好地观察轨道板脱空区域的模态变化。钢轨采用三维梁单元BEAM188模拟；扣件采用线弹性弹簧单元COMBIN14模拟；轨道板、砂浆层和底座板都采用实体单元SOLID45模拟；地基采用线弹性弹簧单元COMBIN14模拟(地基刚度转换成弹簧的刚度)。CRTSⅠ型板式无砟轨道的有限元梁体模型如图2所示。

图2 CRTSⅠ型板式无砟轨道的实体模型(轨道板脱空0.7m时)

CRTSⅠ型板式无砟轨道的模型参数：钢轨线密度为60 kg/m，长度为15.026m，弹性模量206 GPa，泊松比0.3。扣件刚度为50 kN/mm，扣件间距0.629 m。轨道板的长、宽、厚分别为4.962、2.4、0.19 m，弹性模量35.5 GPa，泊松比0.2。砂浆层的长和宽与轨道板相同，厚0.05 m，弹性模量0.3 GPa，泊松比0.15。底座板的长15.026 m、宽2.4 m、厚0.3 m，弹性模量32.5 GPa，泊松比0.2。

3 计算结果与分析

3.1 固有频率

本文使用ANSYS有限元软件，采用BLOCK LANCZOS法对轨道结构进行计算[5]。根据实际经验，一般研究轨道结构的低阶模态，通常取前几阶或者几十阶模态已经满足分析要求，取得足够精确的结果。本文计算了轨道结构的前10阶模态，得到轨道板脱空状况下CRTSⅠ型板式无砟轨道的前10阶固有频率如表1所示，固有频率的变化趋势如图3所示。

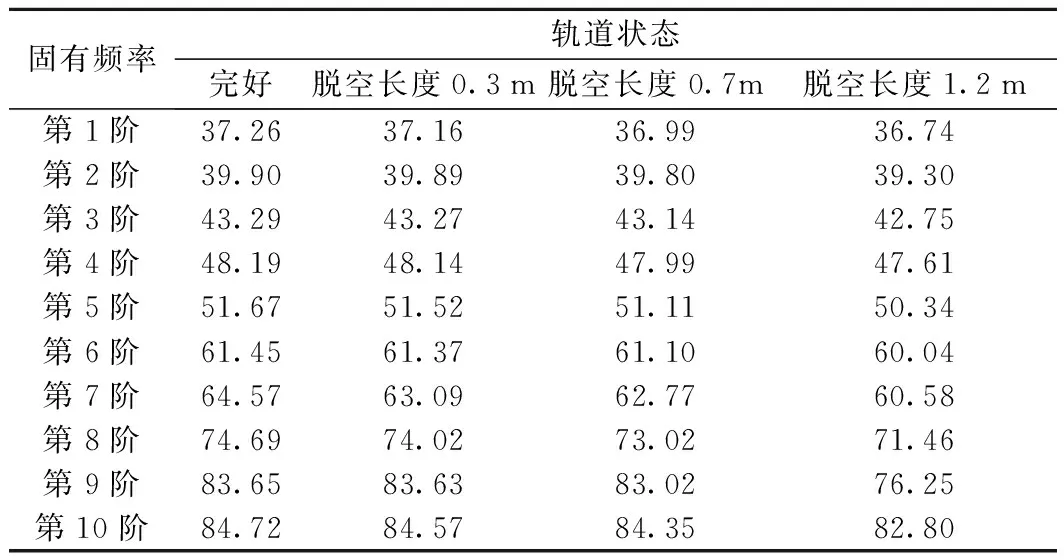
表1 轨道结构的固有频率 Hz

由表1和图3可知：(1)同一种轨道状态下，轨道结构的固有频率随着振动阶数的增加而变大；(2)4种轨道状态下的固有频率随着振动阶数的变化趋势基本相同；(3)随着脱空长度的增加，轨道板同阶固有频率减小；(4)随着振动阶数的增加，轨道板脱空长度越大，其同阶固有频率减小幅度越大。

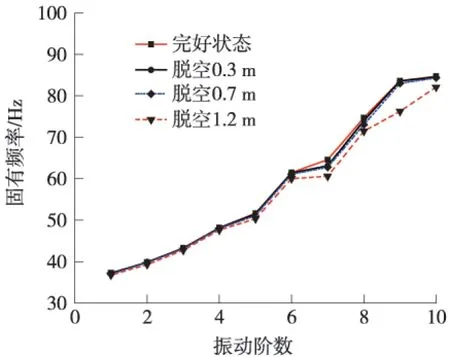
图3 轨道结构的固有频率变化趋势

3.2 振型

振型是结构的相对变形，反映了轨道固有的振动形态，它不随测试条件和测试方法而改变[6]。每一阶固有频率对应一种振型。计算结果表明：CRTSⅠ型板式无砟轨道的振型主要是以弯曲和扭转为主；1阶振型主要是横向振动；2阶振型主要是垂向振动；3阶振型主要是纵向和垂向振动的叠加；4阶振型主要是扭转振动；高阶振型主要是纵向、垂向和横向振动的叠加。

轨道板脱空长度为0.3，0.7，1.2 m时与轨道结构完好时的振型相似。限于篇幅，只列举同阶差异较大的振型进行对比分析。

由图4可知，不同脱空长度下轨道结构的第3阶振型都是垂向振动和纵向振动的叠加，波峰和波谷均出现在中间轨道板的两端。完好时轨道结构的第3阶振型呈余弦曲线形态，而脱空长度为0.3 m时轨道结构的振型呈正弦曲线形态，脱空长度为0.7 m和1.2 m时轨道结构的振型呈余弦曲线形态，说明在脱空长度为0.3 m时，轨道结构的振型会出现较大的差异，而随着脱空长度的增加，轨道结构脱空区域的振动变得剧烈，波峰出现在脱空区域，呈正弦形态。从脱空长度为0.7 m和1.2 m时的轨道结构振型可以看出，波峰出现在脱空区域，该处的垂向位移明显增大。

图4 CRTSⅠ型板式无砟轨道的第3阶振型

由图5可知，轨道结构在完好、脱空长度为0.3 m和0.7 m时轨道结构的振型以轨道中线呈反对称的空间扭转，在中间轨道板两端扭转位移最大；而脱空长度为1.2 m时轨道结构的振型为正弦曲线形态。随着脱空长度的增加，脱空区域的轨道板由扭转振动转变成垂向振动，板端垂向位移陡然增大，此时轨道板与凸台已经分离。

图5 CRTSⅠ型板式无砟轨道的第6阶振型

由图6可知，轨道结构的第7阶振型在完好状态时呈余弦曲线形态，在脱空长度为0.3 m和0.7 m时轨道结构的振型呈正弦曲线形态，在脱空长度为1.2 m时轨道结构的振型以轨道中心线呈反对称的空间扭转。当轨道板脱空长度在0～0.7 m时，轨道结构的振型基本相似，随着脱空长度的增加，振型的波峰逐渐向脱空区域移动，在脱空区域轨道板的垂向位移增大；当脱空长度为1.2 m时，轨道结构由弯曲为主变成以空间扭转为主的振动，在脱空区域轨道板板角受扭翘曲。

图6 CRTSⅠ型板式无砟轨道的第7阶振型

由图7可知，轨道结构在完好时呈正弦曲线形态，在脱空长度为0.3、0.7 m和1.2 m时轨道结构的振型呈余弦曲线形态。随着轨道板脱空长度的增加，轨道结构的振动逐渐变得平缓，振型的波峰逐渐移到脱空区域，轨道结构的波峰由3个(轨道状态完好时)减少到1个(脱空长度为1.2 m时)。当脱空长度为1.2 m时，轨道结构的振型在非脱空区域较为平缓，但是在脱空区域轨道板的垂向位移过大，与凸台已经分离。

图7 CRTSⅠ型板式无砟轨道的第9阶振型

4 结论

(1)4种轨道状态下的固有频率变化趋势基本相同，随着振动阶数的增加，轨道结构的固有频率逐渐增大。

(2)随着轨道板脱空长度的增加，轨道结构的固有频率减小。

(3)轨道结构的低阶振型以单方向(横向、垂向或纵向)振动为主，高阶振型主要是横向、垂向和纵向振动的叠加。

(4)随着脱空长度的增加，轨道结构的同阶振型差异性越来越大，同时振型的波峰逐渐移到脱空区域，轨道板脱空区域的垂向位移增大，在脱空长度为1.2 m时，轨道板与凸台分离。

通过分析CRTSⅠ型板式无砟轨道的轨道板脱空长度对固有频率和振型的影响可知，振型的变化更加显著，可以为轨道结构砂浆伤损的识别提供良好的理论指导。

[1]艾山丁.不同支承方式的橡胶隔振无砟轨道结构振动特性研究[D].北京:北京交通大学，2007.

[2]方远乔，陈安宁，董卫平.振动模态分析技术[M].北京:国防工业出版社，1993.

[3]李成辉.轨道[M].成都:西南交通大学出版社，2004.

[4]刘克飞.框架型板式轨道水泥乳化沥青砂浆伤损及维修标准研究[D].成都:西南交通大学，2013.

[5]商跃进，王红.有限元原理与ANSYS实践[M].北京:清华大学出版社，2012.

[6]梅早临，耿传智，梅早强，等.浮置板轨道结构振动模态分析[J].城市轨道交通研究，2004(5):54-56.

[7]耿传智，田苗盛，董国宪.浮置板轨道结构的振动频率分析[J].城市轨道交通研究，2007(1):22-24.

[8]耿传智，楼梦麟.浮置板轨道结构系统振动模态分析[J].同济大学学报，2006，34(9):1201-1205.

[9]代丰，刘亚航，徐金辉，等.减振型板式轨道的模态分析[J].铁道建筑，2011(9):103-106.

[10]耿传智，曲腾飞，王媛.三种浮置式轨道结构的振动模态对比分析[J].城市轨道交通研究，2012(9):38-42.

[11]刘学毅，王平.车辆-轨道-路基系统动力学[M].成都:西南交通大学出版社，2010.

[12]刘学毅，赵坪锐，杨荣山，等.客运专线无砟轨道设计理论与方法[M].成都:西南交通大学出版社，2010.

[13]梅早临，王娜，陈俭琳.振动模态分析在浮置板轨道结构上的应用[J].铁道标准设计，2014(11):3-6.

[14]陈士通，杜修力，等.结构参数变化对提梁机结构动力特性的影响[J].铁道标准设计，2014(8):95-97.

The Influence of CRTSⅠSlab Track Disengaging on Structural Modal

GUO Li-kang， ZHANG Si-fang， YANG Rong-shan， ZHAO Ping-rui， REN Juan-juan

(MOE Key Laboratory of High-speed Railway Engineering， Southwest Jiaotong University， Chengdu 610031， China)

CRTSⅠSlab Track is selected as the research object. A finite element beam-solid model is established with software ANSYS to analyze the modal of track structure with different disengaging lengths of slab track and provide theoretical guidance for identifying track damages. The results show that with the increase of disengaging length of slab track， the natural frequency of the track structure decreases; the peak of mode shape is moved gradually to the void region， the vertical displacement of the slab track is increasing， and the slab track and cam basement are obviously separated in void region.

Slab track; CA mortar; Disengaging; Modal analysis; Finite element

2014-12-02；

2014-12-16

中央高校基本科研业务费专项资金(SWJTU12BR043)；铁道部科技研究开发计划项目(2011G003)

郭利康(1973—)，男，讲师，E-mail：guolk@home.swjtu.edu.cn。

1004-2954(2015)09-0029-04

U213.2+44

A

10.13238/j.issn.1004-2954.2015.09.007