相邻墩高差对无砟轨道结构不平顺的影响研究
2015-11-25李文斐刘启宾
李文斐,刘启宾
(1.中铁七局集团第三工程有限公司,西安 710032;2.中铁第一勘察设计院集团有限公司,西安 710043)
相邻墩高差对无砟轨道结构不平顺的影响研究
李文斐1,刘启宾2
(1.中铁七局集团第三工程有限公司,西安 710032;2.中铁第一勘察设计院集团有限公司,西安 710043)
针对新建客运专线验收时相邻桥墩高差较大的桥上轨道结构不平顺超限现象,基于有限元分析方法结合实际桥梁工点情况,对简支梁、连续梁及连续刚构典型桥梁工点分别建立有限元分析模型,研究相邻墩高差温度效应对无砟轨道平顺性的影响;相邻墩高差温度效应对轨道10 m弦长不平顺影响很小,对轨道48a弦长不平顺有较大影响,与轨道结构既有不平顺叠加可能超限;轨道480a弦长不平顺的直接影响因素是最高桥墩的高度,与相邻墩高差没有必然关系。
客运专线;无砟轨道;相邻墩高差;温度效应;轨道不平顺
随着我国高速铁路线路不断向西部地区复杂地形的延伸,线路不可避免地会跨越大江、深谷,往往需要修建高墩大跨桥梁[1-4],相邻桥墩存在较大高差的桥梁工点比较普遍。相邻桥墩高差过大时,温度效应会引起各桥墩间产生竖向位移差,进而导致轨面产生附加不平顺[5-7],可能对轨道结构的平顺性产生影响。据现场反应,新建客运专线验收时,相邻桥墩高差较大的桥上轨道结构平顺性往往超限。因此,有必要开展相邻桥墩高差较大时温度效应对无砟轨道结构平顺性的影响。
为研究上述问题,基于有限元分析方法结合实际桥梁工点情况研究了温度效应对相邻墩高差过大的桥梁上无砟轨道结构不平顺的影响情况,为保证墩高差过大的桥梁上无砟轨道平顺性满足规范要求提供参考,同时为解决已出现的不平顺超限情况提供合理的整修建议。
1 研究思路
考虑桥梁结构形式的影响,对简支梁、连续梁及连续刚构3种结构形式的桥梁各选取一个典型工点进行建模研究。
对所建立的有限元模型,先单独施加桥梁梁体自重荷载计算钢轨变形,将此结果作为后续研究内容的基准值;再计算同时施加桥梁梁体自重及温度荷载时钢轨变形情况,此结果与基准值之间的差值即为单独由温度荷载引起的钢轨变形值。研究思路如图1所示。

图1 研究思路
2 典型工点
根据实际桥梁工点情况,对简支梁、连续梁及连续刚构3种结构形式的桥梁各选1个典型工点,如表1所示。
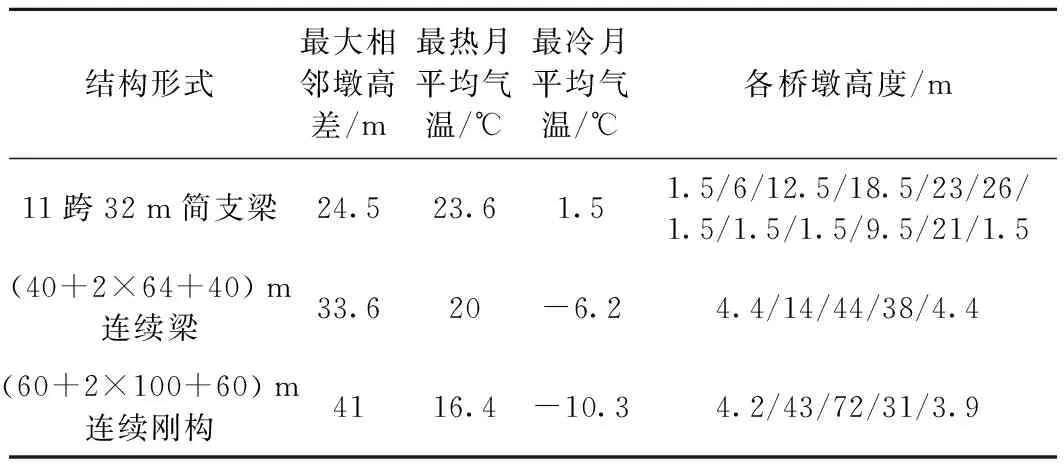
表1 典型工点情况
3 分析模型及荷载参数
3.1 模型基本参数
模型中混凝土密度2 100 kg/m3,线膨胀系数1×10-5m/℃,泊松比0.176;钢轨密度7 900 kg/m3;桥梁、轨道等结构几何参数及自重(包括二期结构恒载)参照设计图纸确定。
3.2 约束条件
本文主要研究的是相邻桥墩高差的温度效应对无砟轨道平顺性的影响,不考虑轨道结构自身存在的不平顺及其他外界因素的影响。因此,本文模型将桥梁墩台底部全约束。
3.3 计算模型
根据典型工点桥梁的实际情况,对简支梁、连续梁及连续刚构分别建立了钢轨-轨道板及底座板-梁体以及桥墩有限元模型。模型中梁体、钢轨、轨道板采用梁单元模拟,桥墩采用只受压不受拉的杆单元模拟。简支梁及连续梁的桥墩与梁体之间采用线性弹簧连接;连续刚构的桥墩与梁体之间固结。各层间采用线性弹簧单元连接,模型示意(以连续梁为例)如图2所示。

图2 有限元分析模型示意
3.4 限值标准
根据规范[8]要求,无砟轨道高低不平顺限值标准为:10 m弦长不平顺限值为2 mm;48a(a为相邻轨枕间距,下同)弦长不平顺限值为2 mm,测点间距8a;480a弦长不平顺限值为10 mm,测点间距240a。
3.5 荷载取值
桥梁墩台为大体积混凝土,其温度变化是一个非常缓慢的过程,几乎不受日温差的影响,只与月平均气温有关[9-12]。根据表1可知,简支梁、连续梁及连续刚构3个典型桥梁工点所处地区月平均气温变化幅度分别为22.1、26.2和26.7 ℃,月平均变化幅度的一半仅为13.4 ℃。考虑无砟轨道结构现场施工温度的要求,取20 ℃作为最大温差荷载进行保守计算。
4 计算结果
4.1 简支梁计算结果
采用所建立的钢轨-轨道板及底座板-梁体以及墩台有限元模型,计算出由桥墩温度变形引起的简支梁上钢轨变形及轨道不平顺,如图3~图5所示。
由图3~图5可以看出:由桥墩温度变化引起的钢轨10 m弦长最大不平顺值为0.059 mm,远小于2 mm的限值;48a最大不平顺值为1.30 mm,小于2 mm的限值;480a最大不平顺可近似认为等于桥梁区域内钢轨的最大垂向位移,即5.15 mm,小于10 mm的限值。
4.2 连续梁计算结果
采用所建立的钢轨-轨道板及底座板-梁体及墩台有限元模型,计算出由桥墩温度变形引起的连续梁上钢轨变形及轨道不平顺,如图6~图8所示。
由图6~图8可以看出:由桥墩温度变化引起的钢轨10 m弦长最大不平顺值为0.037 mm,远小于2 mm的限值;48a最大不平顺值为1.44 mm,小于2 mm的限值;480a最大不平顺可认为等于桥梁区域内钢轨的最大垂向位移,即8.49 mm,小于10 mm的限值。

图3 钢轨变形值

图4 10 m弦长不平顺
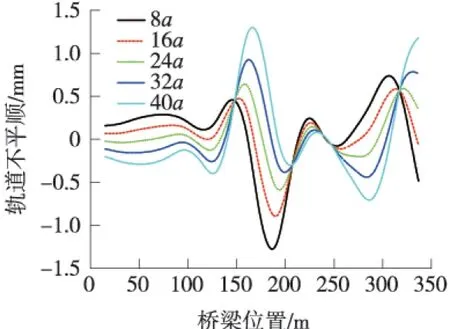
图5 48a弦长不平顺

图6 钢轨变形值

图7 10 m弦长不平顺
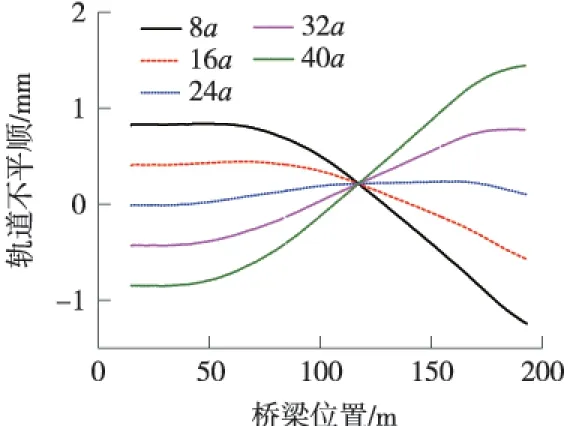
图8 48a弦长不平顺
4.3 连续刚构计算结果
采用所建立的钢轨-轨道板及底座板-梁体及墩台有限元模型,计算出由桥墩温度变形引起的连续刚构桥梁上钢轨变形及轨道不平顺,如图9~图11所示。
由图9~图11可以看出:由桥墩温度变化引起的钢轨10 m弦长最大不平顺值为0.021 mm,远小于2 mm的限值;48a最大不平顺值为1.43 mm,小于2 mm的限值;480a最大不平顺约为12.1 mm,大于10 mm的限值。

图9 钢轨变形值
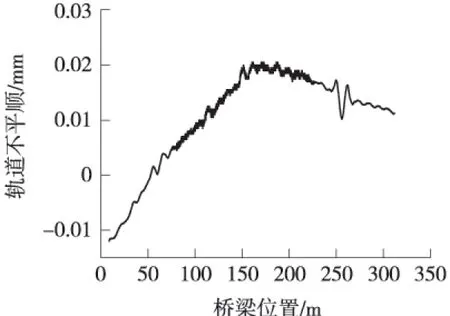
图10 10 m弦长不平顺

图11 48a弦长不平顺
5 结论
本文基于数值分析方法结合典型桥梁工点情况,研究了温度效应对轨道不平顺的影响。根据研究结果,得出的主要结论如下。
(1)相邻墩高差温度效应引起的轨道10 m弦长不平顺最大仅为0.059 mm,远小于2 mm的限值,几乎没有影响。
(2)相邻墩高差温度效应引起的轨道48a弦长不平顺最大为1.44 mm,小于2 mm的限值,但考虑到轨道结构自身存在的不平顺,不同因素导致的轨道结构不平顺叠加可能导致轨道48a弦长不平顺超限。
(3)影响轨道480a弦长不平顺的因素是桥梁中最高墩的绝对高度,与相邻墩高差没有必然关系。
(4)本文典型工点中,轨道480a弦长长波不平顺最大为12.1 mm,超过了规范限值,现场可通过控制无砟轨道在中间月平均气温施工或结合无砟轨道施工时月平均气温等综合因素对轨面设计高程进行修正,避免轨道长波不平顺超限。
(5)对已施工完成但轨道结构不平顺超限的情况,应通过计算分析、现场监测等方法,掌握轨面高程的变化规律,确定合适的轨面高程调整方案。
(6)为保证车辆运行的平顺性、安全性,应尽量避免道岔、伸缩调节器等设备布置在高墩及墩高差大的桥上。
[1]张扬.高墩大跨刚构-连续组合梁桥的设计[J].铁道标准设计,2011(4):80-82.
[2]夏修身,陈兴冲.铁路高墩桥梁基底摇摆隔震与墩顶减震对比研究[J].铁道学报,2011,33(9):102-107.
[3]周雁群,张晔芝,叶梅新,等.铁路桥梁新型柱板式高墩双柱模型的抗震性能[J].中南大学学报:自然科学版,2013(6):2506-2514.
[4]李登科.高墩大跨铁路桥梁动力特性分析[J].铁道建筑,2012(7):1-3.
[5]张梦楠,胡志鹏,巫裕斌,等.高墩大跨桥梁桥墩升温对桥上无缝线路的影响研究[J].铁道标准设计,2014(9):23-26.
[6]段翔远,荆果,徐井芒,等.高墩大跨桥梁变形对无砟轨道的影响[J].铁道建筑,2011(8):1-4.
[7]胡志鹏,谢铠泽,朱浩,等.高墩大跨桥梁桥墩沉降对桥上无缝线路的影响[J].铁道标准设计,2013(10):23-26.
[8]中华人民共和国铁道部.TB10621—2009高速铁路设计规范(试行)[S].北京:中国铁道出版社,2010.
[9]何义斌.混凝土空心高墩温度效应研究[J].铁道科学与工程学报,2007,4(2):63-66.
[10]李坤.高墩大跨连续刚构桥在温度作用下的轨道高低不平顺及对列车的动力影响[D].成都:西南交通大学,2011.
[11]赵亮.混凝土空心墩温度效应有限元分析[D].重庆:重庆大学,2007.
[12]肖新辉,刘扬,郭鑫,等.组合高墩大跨连续刚构桥箱梁日照温度场观测与效应分析[J].铁道科学与工程学报,2014,11(1):10-15.
Study on Track Structure Irregularities Influenced by Differences of Adjacent Pier Heights
LI Wen-fei1, LIU Qi-bin2
(1.The Third Engineering Co., Ltd. of China Railway Seventh Group, Xi’an 710032, China;2.China Railway First Survey and Design Institute Group Co., Ltd., Xi’an 710043, China)
With a view to the overrun of track irregularity influenced by obvious differences between adjacent pier heights on newly built dedicated passenger lines, this paper studies on track structure irregularities influenced by the differences of adjacent pier height by means of FE models of different types of railway bridges based on the finite element method as well as the site situations of bridges. As far as temperature effect is concerned, the differences of adjacent pier heights have little effect on chord irregularity of 10 millimeter, but have large effect on chord irregularity of 48a, and the track irregularity may overrun in the case of superposition with the existing track irregularities. The direct factor of chord irregularity of 480a is the height of the highest pier, and there is no inevitable relation with the differences of adjacent pier heights.
Dedicated passenger line; Ballastless track; Difference of adjacent pier height; Temperature effect; Track irregularity
2014-12-03;
2014-12-11
李文斐(1989—),女,助理工程师,工学学士,E-mail:987289505@qq.com。
1004-2954(2015)09-0022-03
U211.2
A
10.13238/j.issn.1004-2954.2015.09.005
