离散傅立叶变换及其应用

马月红 王雪飞 梁四洋

军械工程学院电子与光学工程系 河北石家庄 050003

离散傅立叶变换及其应用

马月红 王雪飞 梁四洋

军械工程学院电子与光学工程系 河北石家庄 050003

分析了离散傅里叶变换的原理及物理意义，分别将离散傅里叶变换技术应用在双音多频信号检测和雷达信号处理中，加深学生对离散傅里叶变换概念的理解，扩展离散傅里叶变技术应用，达到提高教学质量的目的。

雷达信号处理；离散傅里叶变换；双音多频

仪器设备是高校开展教学、科研和服务社会的物质基础，直接制约着高等教育教学质量和科研水平的提高，做好仪器设备管理工作，使其在人才培养与科学研究中发挥良好效能，是当前各高校普遍面临的共同难题。

信号是信息的载体，它携带着有用信息，如频率、幅度、相位等。信号如果时域特性不明显，我们可以采用傅里叶变换，将时域信号转换到频域中进行分析和处理。一段时域信号如图1所示。

图1 时域信号

从时域图上不能看出信号中含有几个频率分量，有没有噪声存在。显然转到变换域进行分析是一条途径。通过对信号作傅立叶变换后，如图2所示。

图2 频域信号

由于噪声的功率均匀分布在整个频率轴，而信号的频率分量只集中在某个频率附近，表现为较高的谱峰，从而可以将信号从噪声中分辨出来。因此频域中完成对信号的分析和处理，是信号处理的另一个有效的途径。能够将时域中信号转换频域的变换就是傅里叶变换，冈萨雷斯版《图像处理》里面的解释非常形象：一个恰当的比喻是将傅里叶变换比作一个玻璃棱镜。棱镜是可以将光分解为不同颜色的物理仪器，每个成分的颜色由波长（或频率）决定。傅里叶变换可以看作是数学上的棱镜，将函数基于频率分解为不同的成分。当我们考虑光时，讨论它的光谱或频率谱。同样，傅立叶变换使我们能通过频率成分来分析一个函数。

傅里叶变换分为4种［1］：傅里叶级数（FS）、傅里叶变换（FT）、离散时间信号傅里叶变换（DTFT），离散傅里叶变换级数（DFS），这4种傅里叶变换有各自应用领域和特点，都不能用于计算机上进行信号频谱的快速处理，我们希望理想的傅里叶变换是：时域、频域均为有限长且是离散的傅里叶变换对，这就是离散傅里叶变换（DFT）。

1 离散傅里叶级数

连续时间信号时域抽样，数学上就是用时域中的抽样冲激串序列与时域信号相乘，完成时域抽样，得到抽样后的离散时间信号。时域抽样对应频域信号的周期延拓，但序列的频谱仍是连续的频谱，所以需要频域抽样，就是用一系列等间隔的冲激串函数与DTFT相乘。

2 离散傅里叶变换

N点离散傅立叶变换是离散信号的DTFT在一个周期内的N点等间隔抽样，即：

经过频域抽样得到频域离散，时域离散的傅里叶变换对，就是离散傅里叶级数DFS：

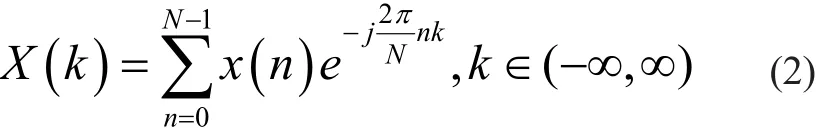
为了适应实际信号处理中，序列有限长特点，将信号加以截断，取DFS一个周期，从而得到DFT变换式：

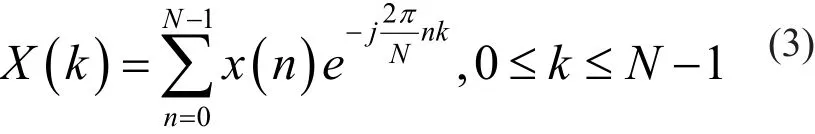
如何根据离散傅立叶变换恢复出原信号呢？离散傅立叶逆变换（IDFT）：

说明：由于时域的离散导致频域的周期，频域的抽样导致时域的周期，所以，尽管DFT的表达式中只取了N点序列值，但是它的时频域都是来自于周期序列的一个周期，即DFT隐含周期性。

离散傅里叶变换的物理意义［2］：序列的N点DFT是序列的连续谱在区间［0，2π］上的N点等间隔抽样，DFT所求的仍是序列频谱，是离散谱。由频域的抽样过程可知，利用DFT可以对信号的连续频谱做近似，可以实现连续频谱的数字化处理。

3 离散傅里叶变换的应用

3.1 DFT在语音信号处理中应用

双音多频（Dual Tone Multi Frequency，DTMF）信号是电话系统中电话机与交换机之间的一种用户信令，由美国AT&T贝尔公司实验室发明。这种信号制式具有很高的拨号速度，且容易自动监测识别，很快就代替了原有的用脉冲计数方式的拨号制式。双音多频的拨号键盘是4×4的矩阵，每一行代表一个低频，每一列代表一个高频。这样8个频率形成16种不同的双频信号。每按一个键就发送一个高频和低频的正弦信号组合，DTMF信号是采用8中取2的方式，从高低两个音组中各取一个音频复合而成来代表0～9的号码和其他功能码，在接收端，要对收到的双音多频信号进行检测，检测两个正弦波的频率是多少，以判断所对应的十进制数字或者符号。显然这里仍然要用数字方法进行检测。检测的方法是用DFT对双音多频信号进行频谱分析，由信号的幅度谱，判断信号的两个频率，最后确定相应的数字或符号。例如，号码‘2’是于由某两个双音多频键的频率相混合叠加，但在时域中很难分辨出，通过离散傅里叶变换将信号转换到频域中，对应的归一化频率分别为≈0.08和≈0.17，对应的实际频率为f1=697Hz和f2=1366Hz相混叠，如图3所示，国际上规定双音多频信号的抽样频率为Fs=8kHzz 。

图3 ‘2’在双音多频信号检测中应用

3.2 DFT在雷达信号处理中的应用

在工程实践中，例如雷达系统中，DFT也发挥着重要的作用。

军事雷达的任务是对运动目标如飞机进行定位。但是大量的地物杂波、云雨杂波、鸟群杂波，同运动目标的回波信号一同进入接收机。运动目标的回波电平往往比杂波电平低很多倍，使运动目标被淹没。这时，在时域中将它们区分已不可能。

根据运动目标和杂波相对雷达的径向运动速度不同，回波具有不同的多普勒频率，我们将转向频域根据多普勒频谱的差别来区分运动目标和杂波。假设运动目标的径向运动为Vr，则回波脉冲串的幅度会受到多普勒频率的调制：

MTD多普勒滤波器组是具有N个输出的横向滤波器组，横向滤波器有N-1根延迟线，每根延迟线的延迟时间为Tr，N个输出端的加权值为：

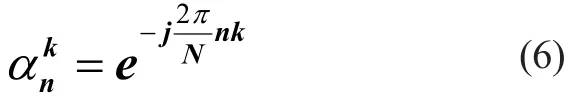
n表示第n个抽头，k的取值从0到N-1，不同的k值对应不同的多普勒器响应，窄带滤波器组就是按DFT定义式展开，加权因子按DFT定义，所以DFT是一种特殊的横向滤波器，当N=8时，8个相邻的窄带滤波器组，如图4所示。

图4 多普勒滤波器组

对同一距离单元的回波脉冲串作频谱分析，用频率过滤的方法检测出运动目标的多普勒频率谱线，滤除干扰杂波的谱线，可使雷达从强杂波中分辨出目标信号。因此，雷达接收机的动目标检测本质上相当于是一种频谱分析仪。

离散傅立叶变换的应用远不止于此，自从1965年Cooly和Turky提出了离散傅立叶变换的快速算法之后，离散时间信号的许多时域运算如卷积、滤波，都可以转化到频域来高效地实现，从而节省运算时间，提高运算效率。凡是在大数据量实时计算的场合，几乎都离不开离散傅立叶变换的影子。因此，可以毫不夸张地说，离散傅立叶变换是数字信号处理的基石，数字信号处理领域核心算法之一。

4 结束语

通过离散傅里叶级数的概念引出离散傅里叶变换的定义，阐述离散傅里叶变换的物理意义，将离散傅里叶变换和实际工程应用相结合，利用Matlab将离散傅里叶变换技术分别应用于语音信号处理和雷达信号处理中，即加深学生对抽象理论的理解，又拓展离散傅里叶变换的实际工程应用背景，有助于提高学生实际动手能力和工程应用能力。

［1］程佩青.数字信号处理教程［M］.第二版.北京:清华大学出版社，2007.

［2］陈后金，薛健，胡健.数字信号处理［M］.第二版.北京:高等教育出版社，2008.

Discrete Fourier Transform and its Application

Ma Yuehong， Wang Xuefei， Liang Siyang
Ordnance Engineering College， Shijiazhuang， 050003， China

This paper describes the principle and the physical significance of the discrete Fourier transform， the application of the discrete Fourier transform technique in the dual tone multi frequency signal detection and radar signal processing， respectively. Enhance the students understanding of the concept of discrete Fourier transform， Expansion technology application of discrete Fourier Transform， to achieve the purpose of improving teaching quality.

radar signal processing； discrete Fourier transform； dual tone multi frequency

2015-01-18

马月红，博士，讲师。