基于无拉力Winkler地基梁的原位测试方法

尹 静，邓荣贵，王 潘，孙春平

(1.西南交通大学土木工程学院， 成都 610031； 2.四川大学水力学与山区河流开发保护国家重点实验室，成都 610065； 3.中建地下空间有限公司，成都 610081)

基于无拉力Winkler地基梁的原位测试方法

尹 静1，2，邓荣贵1，2，王 潘1，2，孙春平3

(1.西南交通大学土木工程学院， 成都 610031； 2.四川大学水力学与山区河流开发保护国家重点实验室，成都 610065； 3.中建地下空间有限公司，成都 610081)

基于梁与无拉力Winkler地基的相互作用，提出一种用于测试基床系数的岩土工程原位测试新方法，对现有测试技术进行补充和发展。在无拉力Winkler弹性地基梁中点处作用一个垂直于地面的集中力，通过测量集中力作用点处的弯矩和垂直于地面的位移，反推出地基的基床系数。讨论测试梁的尺寸和制作材料，介绍试验数据的处理方法。理论计算表明，梁与地基的相互作用范围只与地基系数相关，与力的大小无关，据此可验证测试梁的长度是否符合测试要求，确保测试结果的精确度。

弹性地基梁；原位测试；无拉力Winkler地基；岩土工程

原位测试技术是岩土工程的一个重要分支，是获得岩土体设计参数和土木工程施工质量检验的重要手段。根据我国的国家标准[1]，目前应用于岩土工程原位测试的方法和技术主要包括：载荷试验，触探试验，剪切试验，侧胀试验，应力测试，动力参数测试等。基床系数是应用Winkler弹性地基模型进行设计的重要参数，目前用于确定基床系数的方法有载荷试验、按压缩资料确定、按经验确定以及由土的变形模量和泊松比换算得到等方法[2]。基于无拉力Winkler弹性地基梁理论，提出一种新的梁式载荷原位测试技术，用于测试基床系数，对现有测试技术进行补充和发展。基于Winkler假设的弹性地基梁是一种常用的计算梁与地基相互作用的计算模型，然而，它也存在一些缺陷，例如地基土只能承受梁对其的压力，不能承受拉力，Winkler假设忽略了这一点，因此许多学者对无拉力Winkler地基进行了研究[3-8]。将对单个集中力作用下的无拉力Winkler弹性地基梁进行具体分析，推出梁式载荷原位测试方法的理论公式。

1 测试原理

无拉力Winkler弹性地基模型，即是将地基看成是许多互不联系的弹簧，弹簧只承受压力，不承受拉力，弹簧的刚度即是基床系数k。本文提出如图1的测试技术，1根足够长的梁与地基相互作用，在梁中点作用集中力F，在忽略梁的重力的情况下，梁的两端将翘起，与地面脱离。本试验通过量测梁中点产生的垂直于地面的位移y0、梁中点的弯矩M0，计算地基的基床系数。最后通过推算梁与地基的作用范围c验证梁长是否合适。由于是利用集中力作用下的柔性梁进行测试，可称之为梁式载荷试验。

图1 梁式载荷试验示意

如图1所示，建立原点位于梁中点图示坐标系。计算虽然是基于无拉力Winkler弹性地基模型，但在只有1个集中力作用的情况下，梁与地基的相互作用范围内依然满足一般Winkler弹性地基梁的典型方程

(1)

(2)

式中，b、h、I、E分别为梁的宽度、高度、截面惯性矩及弹性模量。

一个集中力作用下的无拉力Winkler弹性地基梁还满足以下边界条件：x=c处的位移、弯矩、剪力都为0；根据对称性，x=0处的转角为0，剪力为作用集中力的一半。其数学表达式如下

(3)

由上式5个边界条件联立方程(1)可得

(4)

式中，φ1=(sinh(π-λx)+sinh(-λx))sin(λx)

φ2=(cosh(π-λx)+cosh(-λx))cos(λx)

并得到梁与地基相互作用范围

(5)

把式(2)代入式(5)，得

(6)

令式(4)中x=0，可得梁中点处垂直于地面的位移

(7)

把式(2)代入式(7)，得

(8)

对式(4)求二阶导后两端同时乘以-EI，得梁的弯矩

(9)

令x=0，则梁中点处的弯矩为

(10)

把式(2)代入式(10)，得

(11)

从上面可以看出，梁中点的位移和弯矩都和作用力的大小成正比，梁宽对梁承受的弯矩无影响，这些都方便测试人员进行数据的处理。式(8)和式(11)是计算基床系数的两个理论公式。在实际的测试中，梁中点处垂直于地面的位移可以直接测量，弯矩可通过测量应变间接得到，因而采用以上两个公式都可以得到基床系数，且可以进行对比分析。从式(5)可以看出，梁与地基的相互作用范围只与地基系数相关，集中力的大小对其不产生影响。在得到基床系数k后，可以通过其验算测试梁的长度是否合适。并在测试过程中仔细观察梁与地基的相互作用范围，做好记录，以验证测试的精确性。

2 测试梁的制备

由于梁作为测试构件的关键部分，合理的材料和尺寸的选择尤为重要。为满足测试要求，可选择密度在1 g/cm3左右、抗弯模量在1.5 GPa左右的pp塑料制作用于测试的梁。由文献[9，10]可知，基床系数的取值大多位于5×10-6～5×10-5kN/mm3。当h=150 mm时，由式(6)可知c的取值位于673～1 198 mm；当h=100 mm时，c的取值位于496～884 mm。当测试淤泥、松散砂土等构成的基床系数较低的地基时，宜选择梁高和弹性模量都较低的测试梁；反之，则宜选择梁高和弹性模量都较高的测试梁。

以上材料制作的测试梁可用于一般工程的测试，对于大型重要的工程，测试梁可直接用钢筋混凝土制作，此时测试梁的尺寸较大，需要施加的载荷也较大。

3 数据处理示例

假设现有一地基需要测试基床系数，采用的测试梁的参数如表1所示。

表1 测试梁参数

测试中荷载分8级进行加载，每一级施加0.1 kN荷载，施加一级荷载后，待沉降稳定后，测试梁中点位移，并通过测梁中点应变计算其弯矩，然后再施加下一级荷载。测得的数据见表2，从表中可以看出，施加的最大作用力仅0.8 kN。如果采用重力加载，只需要质量80 kg的重物，比较容易满足加载要求。从位移的大小可以看出宜采用千分表进行位移的测量；弯矩采用普通的应变测试仪器就能间接得到。

表2 测试采集的数据

从理论分析知梁中点位移y0和弯矩M0都与作用力F成正比，因此可通过作图法或者最小二乘法处理试验所得数据。图2和图3分别是测得数据的F-y0曲线拟合曲线和F-M0曲线拟合曲线，并在图中标明了采用最小二乘法拟合的曲线的表达式及其相关系数。

图2 F-y0曲线拟合曲线

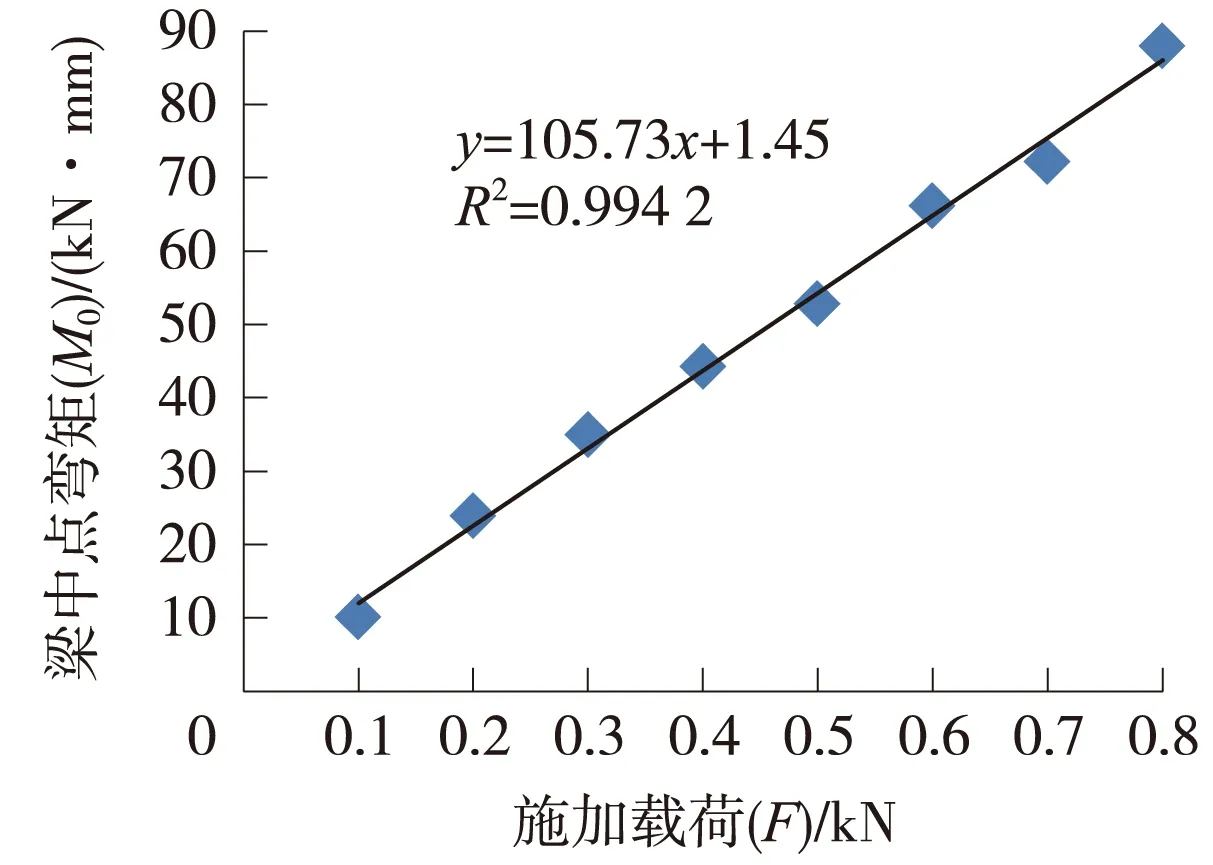
图3 F-M0曲线拟合曲线

由图2和图3中的数据可得

分别代入式(8)和式(11)，得

k1=21 249kN/m3

k2=22 086kN/m3

基床系数取两者的平均值

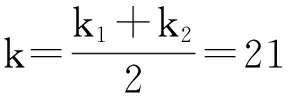
代入式(6)得

c=612.22mm

知l>2c，梁长满足要求。

4 结论与展望

如果梁足够长，单个集中力作用下的Winkler弹性地基梁具有如下特点：梁与地基的作用范围只与地基系数λ相关，即c=π/2λ；梁中点的位移与作用力成正比；梁中点的弯矩与作用力成正比。基于这些特点，提出了一种基床系数原位测试新方法，给出了制作测试梁的建议材料和建议尺寸，并对数据处理进行了示例说明。示例计算表明，该测试方法加载简单，数据采集与处理方便易行，值得在实践中推广应用。

虽然本文推导了梁式载荷试验相应的理论计算公式，如要应用于实践，还需进行相关试验研究，用实测数据验证公式的实用性。

[1] GB50021—2001岩土工程勘察规范[S].北京:中国建筑工业出版社，2002.

[2] 张季容，朱向荣.简明建筑基础计算与设计手册[M].北京:中国建筑工业出版社，1997.

[3] 夏桂云，李传习，张建仁.考虑水平摩阻和双重剪切的弹性地基梁分析[J].土木工程学报，2011，44(12):93-100.

[4] 李永彪，方亚非，郑璐石.无拉力Winkler地基上自由薄板的接触区及其影响因素分析[J].岩石力学与工程学报，1999，18(6):713-717.

[5] 赵明华，马缤辉，罗松南.考虑底面摩阻效应的弹性地基梁微分算子级数法[J].水利学报，2011，42(4):469-475.

[6] 马建军，刘齐建，王连华，等.Winkler地基上有限长梁非线性自由振动[J].工程力学，2012，29(8):58-62.

[7] Nikolaos I， Ioakimidis. Inequality constraints in one-dimensional finite elements for an elastic beam on a tensionless Winkler foundation[J]. Finite Elements in Analysis and Design， 1996(24):67-75.

[8] E.J. Sapountzakis， A.E. Kampitsis. Nonlinear dynam-ic analysis of Timoshenko beam-columns partially supported on tensionless Winkler foundation[J]. Com-puters and Structures， 2010(88):1206-1219.

[9] 仲锁庆，张西平，潘海利.地基土基床系数研究[J].地下空间与工程学报，2005，1(7):1109-1112.

[10]周宏磊，张在明.基床系数的实验方法与取值[J].工程勘察，2004(2):11-15.

[11]王朝晖，李学乾.秦沈客运专线地基系数检测及影响因素探讨[J].铁道标准设计，2001，21(10):43-45.

[12]李俊，强士中，李小珍.地基系数的比例系数m的确定[J].铁道标准设计，2004(11):83-85.

In-situ Testing Method for Tensionless Winkler Foundation Beams

YIN Jing1，2， DENG Rong-gui1，2， WANG Pan1，2， SUN Chun-ping3

(1.School of Civil Engineering， Southwest Jiaotong University， Chengdu 610031， China;2.State Key Lab. of Hydraulics and Mountain River Engineering， Sichuan University， Chengdu 610065， China;3.China Construction Underground Space Co.， Ltd.， Chengdu 610081， China)

Based on the interaction of the beam and the tensionless Winkler foundation， a new method for in-situ testing of the coefficient of sub-grade reaction is proposed to supplement and develop the existing test technology. A concentrated force is acted on the midpoint of the beam on tensionless Winkler foundation to deduce the coefficient of sub-grade reaction by measuring the bending moment and the vertical ground displacement at the point of the force. The proper material and size about the tested beam are discussed， including the method of processing testing data. The results indicate that the interaction range between the beam and the foundation is only related to the coefficient of sub-grade independent of the force scale， which can be used to verify the compliance of the length of the tested beam with test requirement and ensure measurement accuracy.

Elastic foundation beam; In-situ test; Tensionless Winkler foundation; Geotechnical engineering

2014-05-21；

2014-06-27

高等学校博士学科点专项科研基金(20120184110023)；四川大学水力学与山区河流开发保护国家重点实验室开放基金(编号：1208)

尹 静(1982—)，女，博士研究生，E-mail：yinjingswjtu@qq.com。

1004-2954(2015)03-0026-03

TU471

A

10.13238/j.issn.1004-2954.2015.03.006