各向异性亚铁磁链的自旋波理论

彭 亮， 陈 斌，2

（1.上海理工大学 理学院，上海 200093；2.杭州师范大学 理学院，杭州 310018）

近几十年来，一维的亚铁磁链由于表现出很多奇特的物理现象，而引起了人们的极大兴趣和广泛关注.亚铁磁链是由两种自旋不同的磁性离子通过自旋－自旋相互作用（交换积分）而形成的一维晶格，最简单的亚铁磁链由自旋为1和自旋为组成.利用自旋波理论（SWT）［1－2］，可以得到亚铁磁链的长波色散关系与波矢的平方成正比，这与铁磁链的色散关系相同，而反铁磁链的长波色散关系与波矢成正比［3］.这说明虽然亚铁磁链近邻格点上的自旋排列方式与反铁磁链的相同，但是它的物理性质更像是铁磁链.随着人们认识的提高和对亚铁磁链的进一步研究，又产生了许多新的理论，其中包括修正的自 旋 波 理 论（MSWT）［4］、自 洽 平 均 场 理 论（SCMFT）［5］和 薛 温 格 玻 色 子 平 均 场 理 论（SBMFT）［6－7］.近年 来，人 们 又 发 展 了 一 些 新 的 计算方法，例如密度矩阵重整化群（DMRG）［8］方法和量子蒙特卡罗（QMC）［9］方法.随着新的理论和科学的计算方法的出现，人们对亚铁磁链物理性质的了解将会更加全面.

研究各向异性［10］的亚铁磁链，可以提高人们对物质磁性的认识，同时可以为新型磁性材料的研发和应用提供理论上的依据，因此具有理论和实践上的重要意义.出于对上述原因的考虑，本文研究了各向异性亚铁磁链的物理性质.经过研究发现，在各向异性的亚铁磁链中，在一定数值范围内的各向异性因子会对系统中准粒子的激发起到抑制作用，它就像该系统的开关.

1 各向异性亚铁磁链的自旋波理论

对于各向异性的亚铁磁链，其海森堡哈密顿量可表示为

式中，J 是亚铁磁链中两格点磁性离子上电子间的交换积分，且令J＝1；η 是近邻格点间的位置矢差；D 是各向异性因子；是自旋Si在z 轴方向上的投影分量.将系统分为两个子格，其中子格A 的自旋向上，子格B 的自旋向下；N 为每个子格的格点总数，且取晶格长度为单位长度；Si代表子格A中i格点上的自旋，其值为S＝1；si代表子格B中i 格点上的自旋，其值为

将式（1）改写为

子格A：

子格B：

考虑低激发态（即低温区）时，在亚铁磁链中有

利用式（3）和式（4），将亚铁磁链的哈密顿量式（2）展开，并略去算符a，b 的四次项，得到低温近似下的哈密顿量

式中，Z 为晶格的配位数，对于亚铁磁链有Z＝2.对式（5）作傅里叶变换，分别引入子格的自旋波算符ak，bk

利用式（6），各向异性亚铁磁链的哈密顿量式（5）可表示为

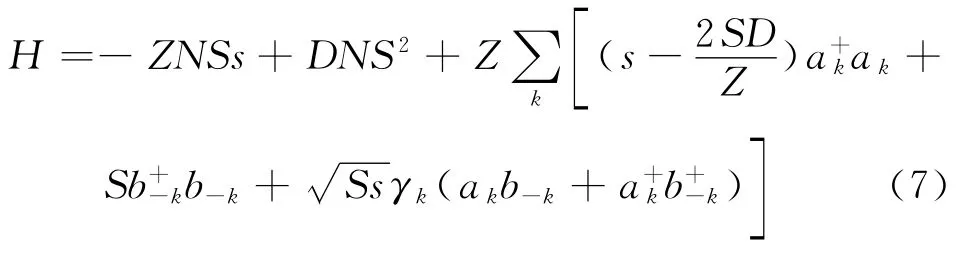
为了消除交叉项，使式（7）对角化，引入玻戈留玻夫正则变换［12］

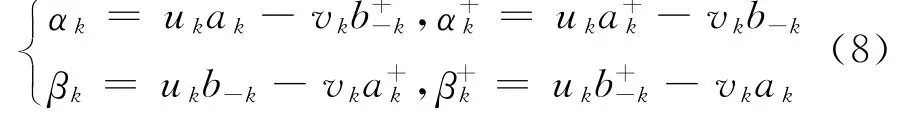
其中，变换系数uk，vk满足关系式

利用式（8），得到对角化的哈密顿量

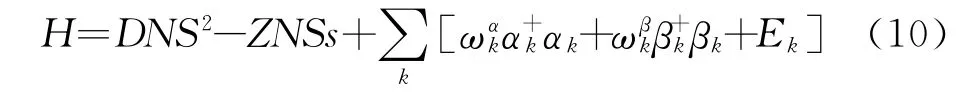
式中

由式（12）可以得出，由于各向异性因子D 的作用，使得一些波矢k 无法在系统中存在，即它会抑制一些准粒子的激发.图1是此系统的两个激发能谱，即声学支（）和光学支.可以看出，随着各向异性因子D 的增加，能谱下降.当D 取0.09时，系统的激发能谱分成了两段.而且D 越大，能谱分得越开，即这种抑制准粒子激发的作用越强.但是，如果D 的取值超过临界值，这种抑制作用又会消失.通过研究，得到在此亚铁磁链系统中存在两个临界值.一般地，此两个临界值可表示为

由以上两式可得到系统中的临界值分别为0.086和2.914.当各向异性因子D 的取值在这两个临界值之外时，即D＜0.086或D＞2.914，它对系统中准粒子的激发没有影响.当D 的取值在这两个临界值之间的时候，即0.086＜D＜2.914，这个各向异性因子就会抑制系统中准粒子的激发.在各向异性的亚铁磁链系统中，各向异性因子D 起到开关的作用.

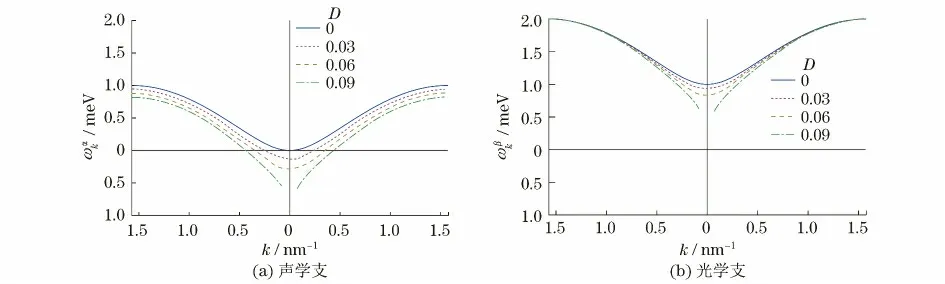
图1 各向异性亚铁磁链的激发能谱Fig.1 Energy spectrum of the anisotropic ferrimagnetic chain

2 各向异性亚铁磁链的物理性质

下面来研究各向异性亚铁磁链的物理性质.由哈密顿量式（10），可以得到该体系单格点的自由能

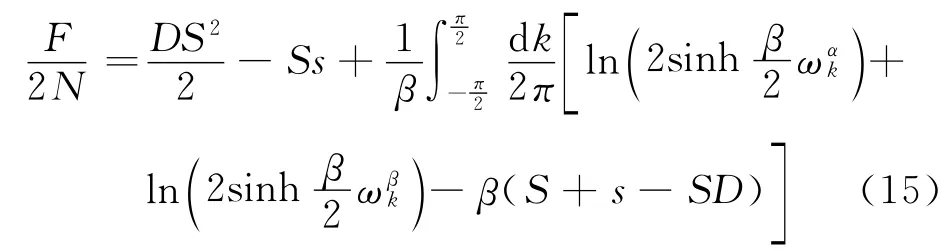
进而，各向异性亚铁磁链的低温比热容由式（16）求得

各向异性亚铁磁链比热容的低温曲线如图2所示（见下页）.可以看到，当温度T＞0.1Κ 时，随着各向异性因子的增加，系统的比热容在增大.各向异性亚铁磁链的比热容与温度成正比，与实验结果相符.

接下来研究外磁场对各向异性亚铁磁链物理性质的影响.处于外磁场H 作用下的各向异性亚铁磁链的哈密顿量可表示为

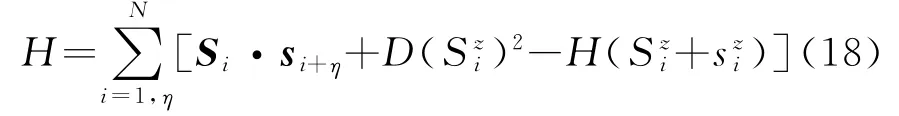
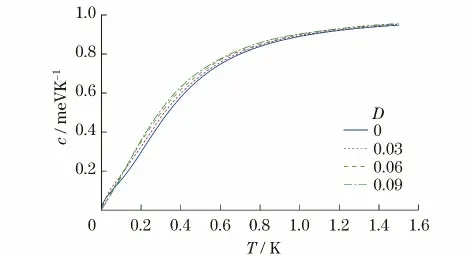
图2 各向异性亚铁磁链的比热容Fig.2 Specific heat of the anisotropic ferrimagnetic chain

式中，取朗德因子g＝1，玻尔磁子μB＝1.利用HP变换，傅里叶变换和玻戈留玻夫正则变换，得到系统对角化的哈密顿量为

式中

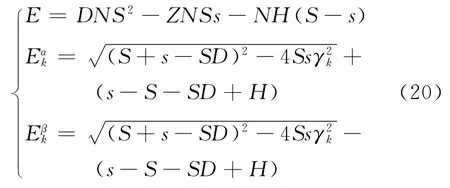
此时体系的自由能可表示为

求得此时系统原胞的磁化强度为

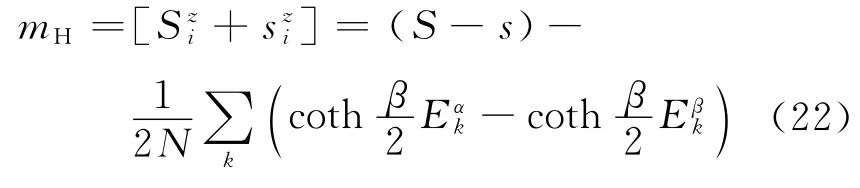
各向异性亚铁磁链的磁化强度曲线如图3 所示，磁化强度曲线在m ＝0.5 处呈现一个平台，满足条件［13］

式中，S 为原胞中所有格点自旋之和；m 为原胞的磁化强度；n 为整数.随着各向异性因子D 的增加，磁化强度平台在缩短，且有消失的趋势，这与实验结果相符.但是，此时各向异性因子D 的取值很小.当D 的取值相当大的时候，所得结果与实验不符，需对自旋波理论进行修正.

图3 各向异性亚铁磁链的磁化强度Fig.3 Magnetization of the anisotropic ferrimagnetic chain

3 结 论

利用自旋波理论，研究了各向异性的亚铁磁链的物理性质.研究发现，各向异性亚铁磁链中存在着两个临界值，当各向异性因子的取值在这两个临界值之间的时候，它会对系统中准粒子的激发起到一定的抑制作用，而且这种抑制作用会随着各向异性因子的增加而增强，这个各向异性因子就像是该系统的开关.同时考虑了外磁场的作用，在外磁场作用下，系统的磁化强度曲线呈现出一个平台，它随着各向异性因子的增加而缩短.

［1］Pati S K，Ramasesha S，Sen D.Low－lying excited states and low－temperature properties of an alternating spin－1／spin－1／2 chain：A density matrix renormalization group study［J］.Physical Review B，1997，55（14）：8894－8897.

［2］Pati S K，Ramasesha S，Sen D.A density matrix renormalization group study of low－energy excitations and low－temperature properties of alternating spin systems［J］.Journal of Physics：Condensed Matter，1997，9（41）：8707－8716.

［3］Auerbach A.Interacting electrons and quantum magnetism［M］.New York：Springer－Verlag，1994.

［4］Yamamoto S，Brehmer S，Mikeska H J.Elementary excitations of Heisenberg ferrimagnetic spin chains［J］.Physical Review B，1998，57（21）：13610－13613.

［5］Chen B，Zhang Z F，Han R S.Self－consistent meanfield theory for spin 1 and spin 1／2ferrimagnetic chain［J］.Physica B：Condensed Matter，2004，349（1）：1－9.

［6］Wu C J，Chen B，Dai X，et al.Schwinger boson mean field theory of the Heisenberg ferrimagnetic spin chain［J］.Physical Review B，1999，60（2）：1057－1060.

［7］Li Y X，Chen B.Schwinger－boson mean－field theory of an anisotropic ferrimagnetic spin chain［J］.Physics Letter A，2010，374（34）：3514－3519.

［8］Yamamoto S，Fukui T，Sakai T.Characterization of ferrimagnetic Heisenberg chains according to the constituent spins［J］.The European Physical Journal B，2000，15（2）：211－219.

［9］Brehmer S，Mikeska H J，Yamamoto S.Low－temperature properties of quantum antiferromagnetic chains with alternating spins s＝1 and s＝1／2［J］.Journal of Physical：Condensed Matter，1997，9（19）：3921－3924.

［10］谢桂兵，耿滔，王燕.铁磁共振下磁各向异性材料的负折射特性研究［J］.上海理工大学学报，2013，35（5）：439－442.

［11］Holstein T，Primakoff H.Field dependence of the intrinsic domain magnetization of a ferromagnet［J］.Physical Review，1940，58（12）：1098－1113.

［12］李正中.固体理论［M］.2 版.北京：高等教育出版社，2002.

［13］Sakai T，Okamoto K.Quantum magnetization plateau of an anisotropic ferrimagnetic spin chain［J］.Physical Review B，2002，65（21）：4403－4406.