基于Vague集及隐马尔科夫的大学生心理危机预测

高广银， 刘 姜， 丁 勇

（1.南京理工大学 泰州科技学院 计算机科学与技术系，泰州 225300；2.上海理工大学 管理学院，上海 200093）

大学校园里因心理问题引发的心理危机事件呈上升趋势，各种从压力、抑郁到自伤、他伤等失控行为并不鲜见.专家学者积极研究大学生心理健康教育，分析影响心理健康的因素，并提出了从学生心理委员到学校心理咨询中心层层报送的高校心理危机监控报送体系［1］，及以建设校园文化、确立价值观导向为核心的心理危机干预机制［2］，这促进了人们对心理危机问题的关注和思考.然而，这些研究大都停留在心理健康教育的层面，缺乏有效的手段预知大学生是否产生了心理危机.人的心理活动极其复杂，其变化过程也不可见，通过心理危机预测能够尽早地发现问题，及时采取干预措施，有效避免心理危机形成、恶化带来的后果.

隐 马 尔 科 夫 模 型（hidden Markov model，HMM）［3］作为一种统计分析模型，创立于20世纪70年代，80年代得到了传播和发展，并应用于语音人工合成、图像处理、模式识别及生物信号处理等领域［4］.近年来，该模型被应用于金融市场的波动性分析、经济预算、网络安全［5］、人的行为分析［6］等诸多领域，从而被证明对于解决一类问题，即系统中表层可见事件可能由低层隐藏状态引发，具有重要意义.

本文将隐马尔科夫模型应用于高校学生心理危机的预测，在分析影响大学生心理健康因素的基础上，利用Vague集理论［7］建立核心因素集，由此确定可观察序列集，建立隐马尔科夫模型，对模型参数进行训练，并将训练后的模型应用于心理危机预测.实例分析结果表明基于该模型预测大学生心理危机是可行的.

1 心理危机因素

1.1 影响大学生心理健康的因素分析

在大学生心理健康教育研究中，不同的学者由于研究工具和研究对象的不同而得出了许多不同的结论.针对综合性大学新生的心理调查发现，大学新生的主要心理问题是学习压力大、人格缺陷和人际交往障碍［8］.基于高职学生的研究表明，导致心理压力因素主要是学习、就业和情感等［9］.这些研究成果都从不同层面指出了影响大学生心理健康的因素，但是关于这些因素对心理危机产生的影响程度并未阐明.本文首先在已有研究成果的基础上，结合某独立学院的实际情况，通过与学院心理辅导教师和辅导员的访谈，概括影响大学生心理健康有4大因素共19项指标：家庭因素（氛围、父母教养方式、经济条件、重大变故）、社会因素（价值多元化、扩招学费高、竞争就业难）、学校因素（学习压力、教育方式、管理制度、设施条件、教工素质）及个人因素（认知方式、应对方式、归因方式、自我定位、人际关系、社会认同、生理疾病）；其次基于Vague集对这些因素约简得出影响心理危机产生的核心因素［10］.

1.2 建立核心因素集

根据上述分析的19项指标，可以建立大学生心理健康影响因素的完备集D＝｛a1，a2，…，am｝，其中m ＝19.然而这些因素对于心理危机的形成作用不等，只有那些起关键作用的因素对于开展心理危机预测有意义，即核心因素.

首先，组建能够代表心理健康教育各层面的专家组，组员有市教育局心理咨询师、高校心理学专业教师、辅导员、其他心理健康教育工作者及家长代表共n 名，并请这n 位专家，对m个因素的重要性表态，分重要、不重要和不好判断，并分别记为1，－1和0.其次，汇总专家意见，确定每个因素的重要程度，并用Vague集表示［11］.

从而，因素完备集D 到核心因素集C 的关系R（D→C）可以定义为一Vague 集关系.每一指标ai（i＝1，2，…，m）的 重 要 程 度 可 以 表 示 为（t（ai），1－f（ai））.其中，t（ai）表示指标ai对大学生心理危机产生重要影响的成分；f（ai）表示指标ai不对大学生心理危机产生重要影响的成分.t（ai）及f（ai）定义如下：

最后，计算核函数H（ai），并给出重要性标准α（0＜α＜1），当H（ai）≥α 时，ai入选核心因素集C.核函数H（ai）可以解释为因素ai对心理危机产生重要影响的重要程度，其定义为

根据经验，取α＝0.3，并用H（ai）≥α 作为判断准则，从19个因素中筛选出5个核心因素，得到核心因素集C＝｛父母教养方式、重大变故、竞争就业难、教工素质、人际关系｝，如表1所示（见下页）.

表1 专家评分表Tab.1 Expert score table

2 心理危机预测建模

2.1 隐马尔科夫模型

隐马尔科夫模型是一种用参数表示的用于描述随机过程统计特性的概率模型，是一个双重随机过程.它由马尔科夫链和一般随机过程两部分组成，其中马尔科夫链用转移概率矩阵描述状态的转移，而一般随机过程则用观察概率矩阵描述状态与观察序列间的关系［12］.HMM 定义如下：

a.X 表 示 一 组 状 态 集 合，X ＝｛S1，S2，…，SN｝，状态数为N，并用qt表示t 时刻的状态；

b.O 表示一组可观察序列的集合，O＝｛V1，V2，…，VM｝，其中，M 是从每一个状态可能输出的不同观察值数目；

c.状态转移概率矩阵A＝｛aij｝，其中，aij＝P｛qi＋1＝Sj｜qi＝Si｝，i≥1，j≤N；

d.状态Sj的观察概率矩阵B＝｛bj（k）｝，表示状态Sj输出相应观察值的概率，其中bj（k）＝P｛Ot＝Vk｜qt＝Sj｝，1≤j≤N，1≤k≤M；

e.初始化状态分 布π＝｛πi｝，πi＝P｛q1＝Si｝，1≤i≤N.

由上，HMM 可以定义为一个五元组λ＝（X，O，π，A，B），并简写为λ＝（π，A，B）.

HMM 主要解决3类问题：评估、解码和学习.

a.评估.给定模型参数λ＝（X，O，π，A，B）及观察序列O＝｛V1，V2，…，VM｝，根据此模型计算此观察序列的概率P（O｜λ）.

b.解码.根据给定的模型λ＝（X，O，π，A，B）及一个观察序列，选择最符合该观察序列的状态序列.

c.学习.给出一个观察序列，调整模型的参数A，B，π，使得P（O｜λ）最大.

2.2 初始模型的建立

建立预测大学生心理危机的隐马尔科夫模型，即要确定隐马尔科夫模型的5个要素，可通过5个步骤完成［13］.

步骤1 通过心理专家对大学生心理状态进行评估，确定其状态的几种可能情况，一般描述为心理健康、心理亚健康、心理危机等，以此作为预测大学生心理危机的隐马尔科夫模型的隐状态，定义隐状态集合为：X＝｛S1，S2，…，SN｝，N＝3，其中，S1，S2，S3分别为心理危机、心理亚健康、心理健康3种心理状态.

步骤2 将核心因素集C＝｛父母教养方式，重大变故，竞争就业难，教工素质，人际关系｝记为C＝｛a1，a2，a3，a4，a5｝，为了便于描述这些因素对心理危机产生的影响以及建立隐马尔科夫模型，本文采用这5个因素的一个组合V 表示，定义为

其中显然，V 是由0或1组成、长度为m 的串，且可以通过学生问卷调查或心理测试等方式获得，从而可以作为隐马尔科夫模型的可观察状态，定义可观察序列集合为：O＝｛V1，V2，…，VM｝，M＝2m.

步骤3 设置初始状态转移概率矩阵

步骤4 根据大学生心理健康评估历史数据分别统计心理健康、心理亚健康、心理危机3种状态下各影响因素组合V，即观察状态的概率B.

步骤5 设置π＝｛1，0，0｝，即假设大学生入校时不存在心理危机问题.

通过以上步骤，预测大学生心理危机的隐马尔科夫初始模型λ＝（π，A，B）已建立，然而其中的参数未进行优化，无法真正应用于心理危机的预测中，因此需要对模型中的参数进行训练和优化.

2.3 模型训练

初始模型λ＝（π，A，B）经过Baum－Welch算法优化后，可以得到模型λ′＝（π′，A′，B′），其参数经过大量训练数据训练得出，具体的训练优化流程如下：

a.引入两个变量εt（i，j）和γt（i，j），其中

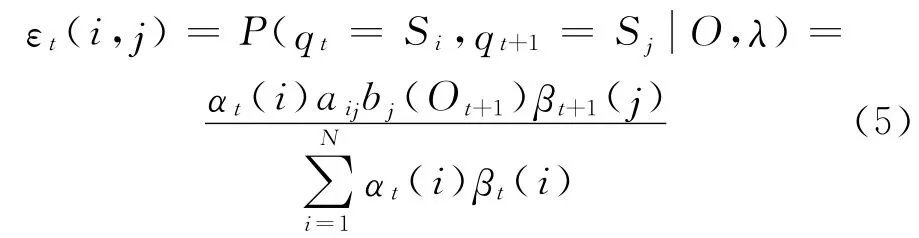
式中，εt（i，j）为给定隐马尔科夫模型λ 和观察序列O 的前提下，在t 时刻状态为Si且在t＋1时刻状态为Sj的概率；αt（i）为前向变量，表示t 时刻状态为Si，且t 时刻之前（包括t 时刻）满足给定观测序列的概率；βt（i）为后向变量，表示t 时刻状态为Si，且t 时刻以后满足给定观测序列的概率.

式中，γt（i）为给定隐马尔科夫模型λ 和观察序列O 的前提下，在时刻t 状态为Si的概率.合并后得到

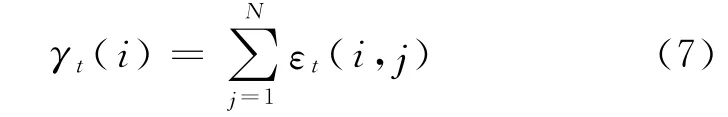
b.利用前面定义的变量εt（i，j）和γt（i），可得出状态转移概率矩阵A 的优化算法，具体推导过程为

最后得出经过优化后的aij为

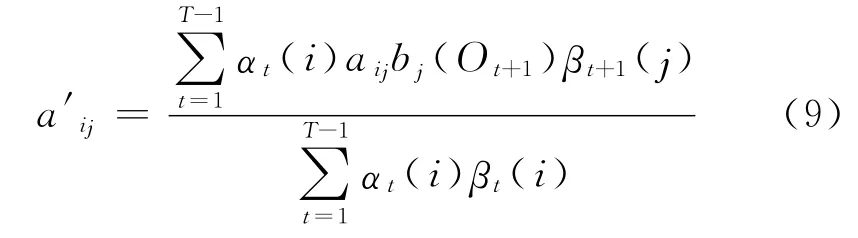
c.观察值概率分布B 的优化算法为

d.初始状态概率分布π 的优化算法为

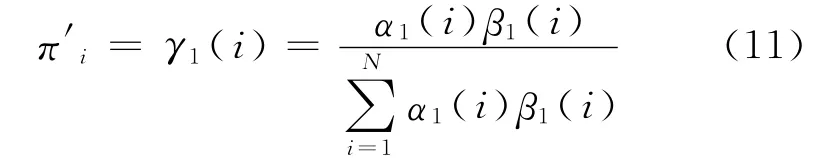
通过式（9）、式（10）及式（11）分别对转移概率矩阵A、观察概率矩阵B 及初始化状态分布π 进行优化，得到训练后的模型λ′＝（π′，A′，B′），并用于心理危机预测.

2.4 模型应用

模型λ′＝（π′，A′，B′）应用于心理危机预测，根据核心因素的观察序列，寻找生成该观察序列最可能的隐状态序列，即学生的心理状态，达到预测的目的.这属于隐马尔科夫模型中的解码问题，使用Viterbi算法解决，具体算法过程如下：

a.t＝1时，δ1（j）＝π（j）bjk1；

b.t＞1时，δt（j）＝maxi｛bjktδt－1（i）aij｝；

c.t＝T 时，计算δT（j），选择包含最大局部概率的状态，相应的局部最优路径即为全局最优路径；

d.反 向 指 针φt（j）用 于 回 溯，φt（j）＝arg maxi｛δt－1（i）aij｝.

3 实例分析

模型训练及预测程序基于Eclipse平台，采用Java语言及google jahmm－0.6.1包编写.

实例分析数据来自南京理工大学泰州科技学院大学生心理健康教育与咨询中心近两年来学生心理健康评估原始记录约2 000条.根据前文定义的隐状态集合及可观察序列集合对心理健康评估原始数据进行预处理，得到观测符号对应隐状态的记录，其中观察符号是由0，1组成的长度为5的字符串，共32种，隐状态共3种.将预处理后的数据分成两部分：训练数据和测试数据，分别用于模型训练和预测.

分析结果表明，随着训练样本容量的增加，模型的预测准确率逐步提高，并在达到一定数目后趋于稳定，模型是收敛的，如图1所示.使用单个因素的预测效果远低于使用核心因素集，使用核心因素集的预测准确率能够达到90%以上；另一方面，各因素对预测结果的影响程度是不等的，其中“父母教养方式、重大变故、竞争就业难”这3个因素对预测影响较大.

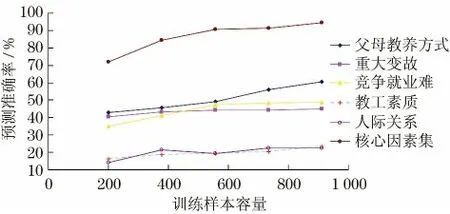
图1 基于各因素及核心因素集的预测结果Fig.1 Prediction result based on single factor and core factor set

此外，将该模型应用于在校一年级学生心理危机预测，并与心理卫生测试国际通用标准UPI筛选及SCL－90进行比较，其中UPI是大学人格问卷，SCL－90是心理健康测试量表.从表2中数据可以看到心理卫生测试标准的评测结果具有一致性，即UPI与SCL－90对S1，S2，S3这3种状态样本数的统计结果保持一致.但两者都倾向于将样本由S3评测为S2，由S2评测为S1，继而采取后续约谈等干预手段实施心理健康教育；使用HMM 的预测结果与使用测试标准的评测结果基本吻合，且准确率更高一些，表3中准确率的比较也说明了这一点.

表2 实际预测与标准评测Tab.2 Practical prediction and standard evaluation

表3 准确率对比Tab.3 Accuracy comparison among various methods %

4 结束语

为了解决大学生心理危机预测问题，基于Vague集理论分析并建立了影响大学生心理危机的核心因素集，构造了可观察序列集合，建立了预测大学生心理危机的隐马尔科夫模型.运用Baum－Welch算法对模型参数进行训练，并将训练后的模型应用于心理危机预测，通过基于真实数据的实例分析验证模型的正确性.研究结果表明，单个因素无法准确预测，而采用核心因素集能够显著提高预测的准确率，且各因素对预测所起的作用不等.下一阶段将继续研究更合理的因素组合，对模型进行优化，运用序列挖掘方法挖掘大学生心理活动变化的规律，细化隐状态及隐状态之间的转移，提高预测的精度，通过反向算法还原心理危机的产生过程，分析并给出合理的干预措施建议.

［1］王群，刁静，林磊.大学生心理危机预防与干预体系的研究［J］.上海中医药大学学报，2013，27（2）：88－92.

［2］陈小红，李三岗.生命教育视角下大学生心理危机及其干预探析［J］.渭南师范学院学报，2013，28（12）：78－80.

［3］Rabiner L R.A tutorial on hidden Markov models and selected applications in speech recognition ［J］.Proceedings of the IEEE，1989，77（2）：257－286.

［4］Yamato J，Ohya J，Ishii K.Recognition human action in time sequential images using hidden Markov model［C］∥Proceedings of IEEE Conference on Computer Vision and Pattern Recognition.Champaign，IL：IEEE，1992：379－385.

［5］Bilmes J A.What HMMs can do ［J］.IEICE Transactions on Information and Systems，2006，89（3）：1－24.

［6］邬书跃，田新广.基于隐马尔可夫模型的用户行为异常检测新方法［J］.通信学报，2007，28（4）：38－43.

［7］Gau W L，Buehrer D J.Vague sets ［J］.IEEE Transactions on Systems，Man and Cybernetics，1993，23（2）：610－614.

［8］刘伶俐，王朝立，于震.CHMM 语音识别初值选择方法 的 研 究［J］.上 海 理 工 大 学 学 报，2012，34（4）：323－326.

［9］马广水.基于系统动力学大学生心理安全预警技术研究［D］.武汉：武汉理工大学，2012.

［10］林志贵，徐立中，刘英平.Vague集理论及其在模糊信息处 理 中 的 应 用［J］.信 息 与 控 制，2005，34（1）：54－59.

［11］张丽，马良.基于粗糙集属性约简的模糊模式识别［J］.上海理工大学学报，2003，25（1）：50－53.

［12］彭子平，张严虎，潘露露.隐马尔科夫模型原理及其重要应用［J］.计算机科学，2008，35（4）：138－139.

［13］闫新娟，谭敏生，严亚周，等.基于隐马尔科夫模型和神经网络的入侵检测研究［J］.计算机应用与软件，2012，29（2）：294－297.