拉盖尔-高斯涡旋光束的传输特性研究
2015-11-22侯乐鑫董祥美
侯乐鑫, 耿 滔, 董祥美
(上海理工大学 光电信息与计算机工程学院,上海 200093)
涡旋光束是具有连续螺旋状相位分布的光束,其光场表达式中有一项形式为exp(i lφ)的相位因子,其中,l 称为拓扑荷,φ 为柱坐标系中的角向坐标。涡旋光束的每个光子携带lħ 的确定光子轨道角动量,ħ 为约化普朗克常量。早期涡旋光束主要集中应用于光学微操控,如对微粒和原子的光陷阱[1]、捕获和 引 导 粒 子[2-3]、驱 动 微 粒 旋 转[4-5]等。近年来,研究者发现其可以用于保密[6-7]、高密度通信[8-10],因此,越来越多的研究开始集中到涡旋光束的传输特性方面[11-13]。
基模高斯光束在自由空间传播时能保持其自身的表达形式不变,因为,其本身就是一个自傅立叶变换过程。然而对于高阶涡旋光束在自由空间的传播是否也能保持其自身表达形式的不变性,针对这一问题的研究较少。最近,文献[13]利用菲涅耳衍射理论研究了拉盖尔-高斯涡旋光束的传输特性,由于衍射积分的复杂性,文献[13]中的入射面电场只考虑了n=0的情况,即拉盖尔多项式恒等于1。n为拉盖尔多项式过零次数.因此,得到的结果无法应用到任意阶(n≠0)的拉盖尔-高斯涡旋光束。
本文从菲涅耳衍射理论出发,以自由空间为例,利用柯林斯公式推导出任意阶拉盖尔-高斯光束的传播形式,证明了任意阶拉盖尔-高斯涡旋光束在自由空间传播时都能保持自身表达形式的不变性。更为重要的是,本文的研究方法可以拓展到满足傍轴条件的任意光学系统。
1 理论推导
在傍轴条件满足的情况下,光学系统对光线的变换作用可由其变换矩阵表示,如图1所示。
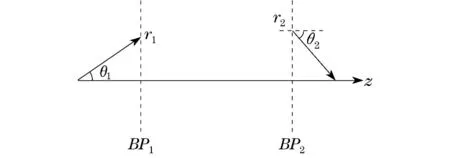
图1 光学系统对光线的变换作用Fig.1 Transformation by the optical system
r 为光线离轴线z 的距离,θ 为光线传播方向与z 轴的夹角,BP1和BP2分别为入射面和出射面。入射光线与出射光线的参数关系可表示为

式中,T 为光学系统的光学变换矩阵;A,B,C,D 是矩阵T 的元素,取值由光学系统决定。
由光学变换矩阵原理可知,无论一个光学系统有多复杂,只要知道其光学变换矩阵,即可求得出射光线的位置与方向。利用光学矩阵变换原理可以大大简化光线在复杂光学系统中的传输问题。
将以上光学矩阵原理应用于菲涅耳衍射公式
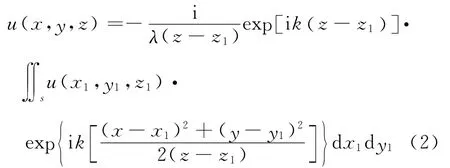
得到柯林斯公式[14]

式中,λ 为波长;k=2π/λ;u 为光束的横向复振幅分布;观察平面坐标由x,y,z 表示;入射平面坐标由x1,y1,z1表示.
先考虑厄米-高斯波在自由空间的传播行为,令入射面z1=0在高斯光束束腰处,则有
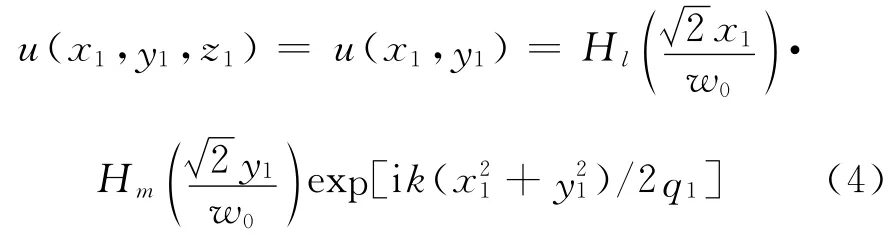
式中,w0为束腰半径;为模式指数(l,m =0,1,…);Hl(·),Hm(·)为厄米多项式。
将式(4)代入式(3),整理可得观察平面z 上的场分布

其中
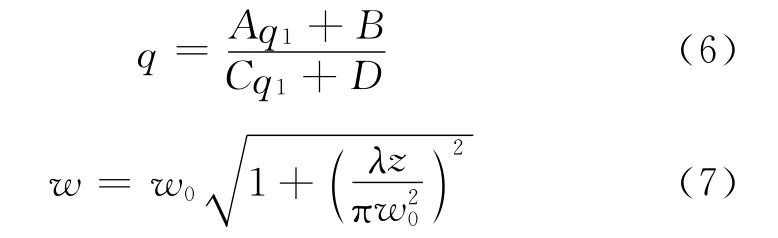
在自由空间传播时,有A=D=1,B=z,代入式(5)并整理得
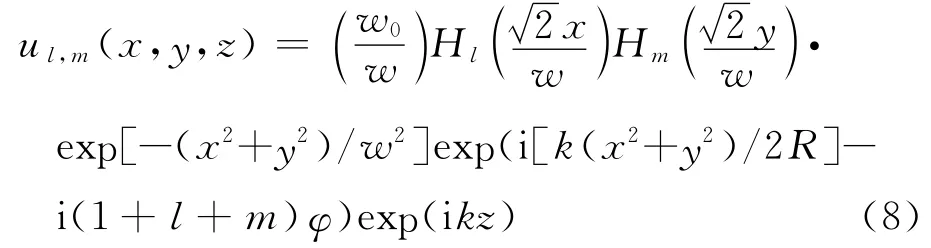
其中
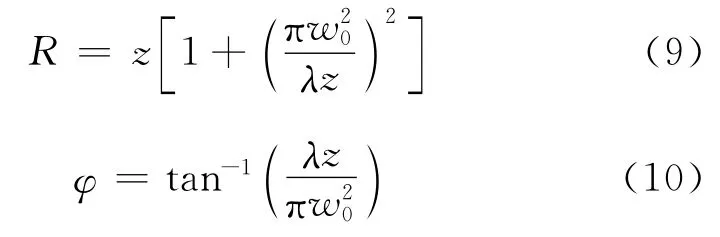
式(8)即为厄米高斯光束的电场分布。
拉盖尔多项式可以用厄米多项式展开,其展开式为[15]
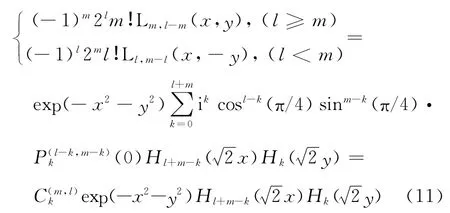
其中
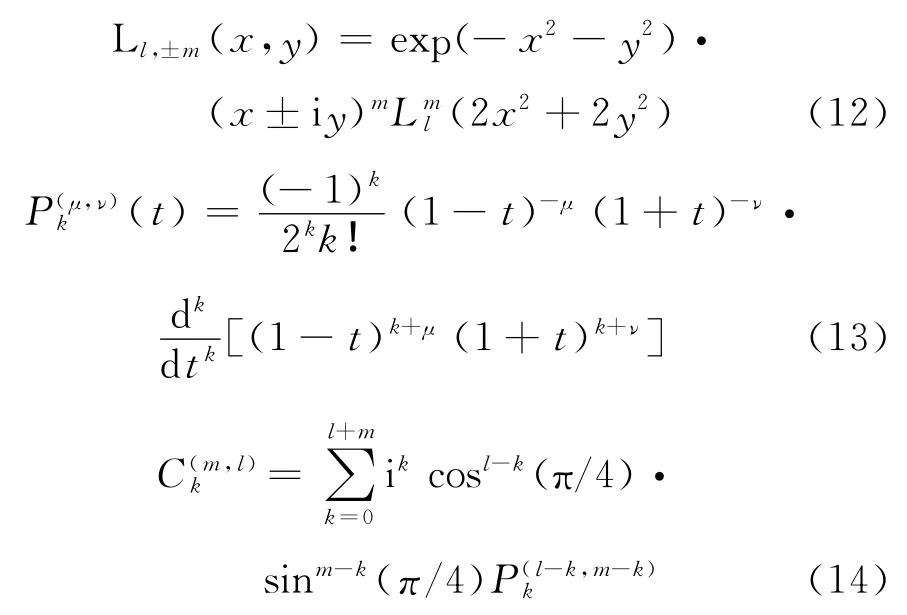
式中,Ll,±m(x,y)即拉盖尔-高斯光束的横模场分布;)为拉盖尔多项式;为Jacobi多项式。
由式(11)可知,在入射面(z=0)的任意阶拉盖尔-高斯涡旋光场可以写成厄米高斯光的线性组合,由于积分后不改变线性叠加特性,将式(11)代入式(8),然后将直角坐标转化为柱坐标,并进行化简整理,得到任意阶拉盖尔-高斯光束经自由空间传播后在任意z 平面上的场分布
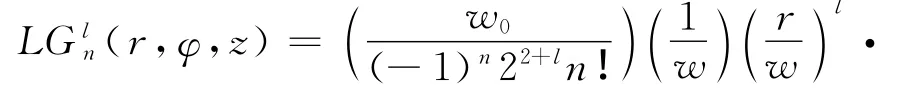
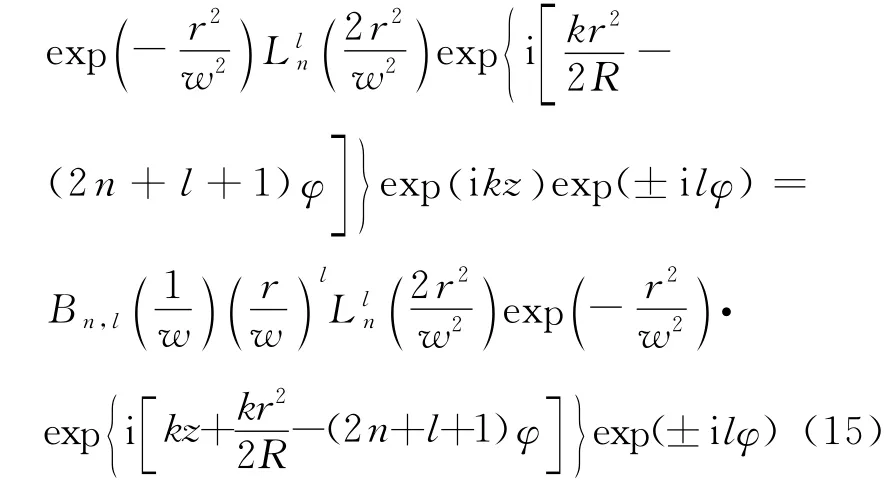
通过求解傍轴条件下的波动方程,获得拉盖尔-高斯光束的电场形式为[16]

式中,An,l为常系数。
比较式(15)和式(16)发现,它们的表达形式完全一样,这就证明了任意阶拉盖尔-高斯涡旋光束在自由空间的传播能保持自身表达形式的不变性。
2 仿真模拟和分析
图2为涡旋光束在自由空间传播1m 后的强度分布图,由于相位奇点的存在,中心都为暗核,横截面上径向截线圆数由拉盖尔多项式的过零次数决定,取决于n。光束的扩散速度与阶数有关,在同样的衍射距离上,n 值相同时,l 值越大,则光束半径越大;l值相同时,n 值越大,光束半径越大。
在源平面上,光束相位因子为exp(±i lφ),其等相位线为由中心出发沿半径方向的直线,同时n决定平面上相位分布在径向上的截线数。经过空间传输之后,光束相位分布发生了变化,其横截面上的等相位线不再是直线。由式(15)可知,光束经自由空间传播之后光束横截面上的相位因子变为
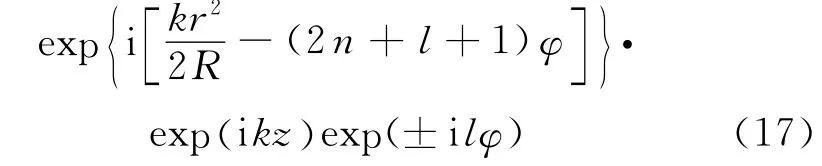
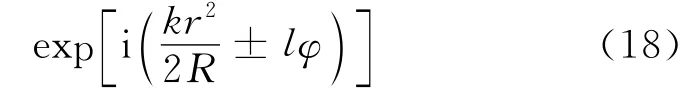
在z=z1处,exp[-i(2 n+l+1)φ]exp(i kz1)为常相位项,不影响相位分布,此时相位分布由决定。由式(18)可知,当光束离开源平面后(z=0),任意点的相位分布不仅与φ 有关,还受到了r的影响,相位随着r 的增大逐渐增加,造成了等相位线的弯曲,弯曲方向由拓扑荷数的正负决定。当n≠0时,拉盖尔多项式每次过零,相应位置增加π的相位差,如图3所示(见下页)。在源平面上,等相位线为由坐标中心出发的射线。等相位线周期数等于拓扑荷l的绝对值。经过一段距离的传播后,光束横截面上等相位线发生弯曲,弯曲方向取决于l的正负取值。在z=1m处的横截面上,当l 为正时,等相位线的弯曲方向为逆时针方向;当l 为负时,等相位线弯曲方向为顺时针方向。n=3时,拉盖尔多项式3次过零,横截面上相位分布发生3次跃变。
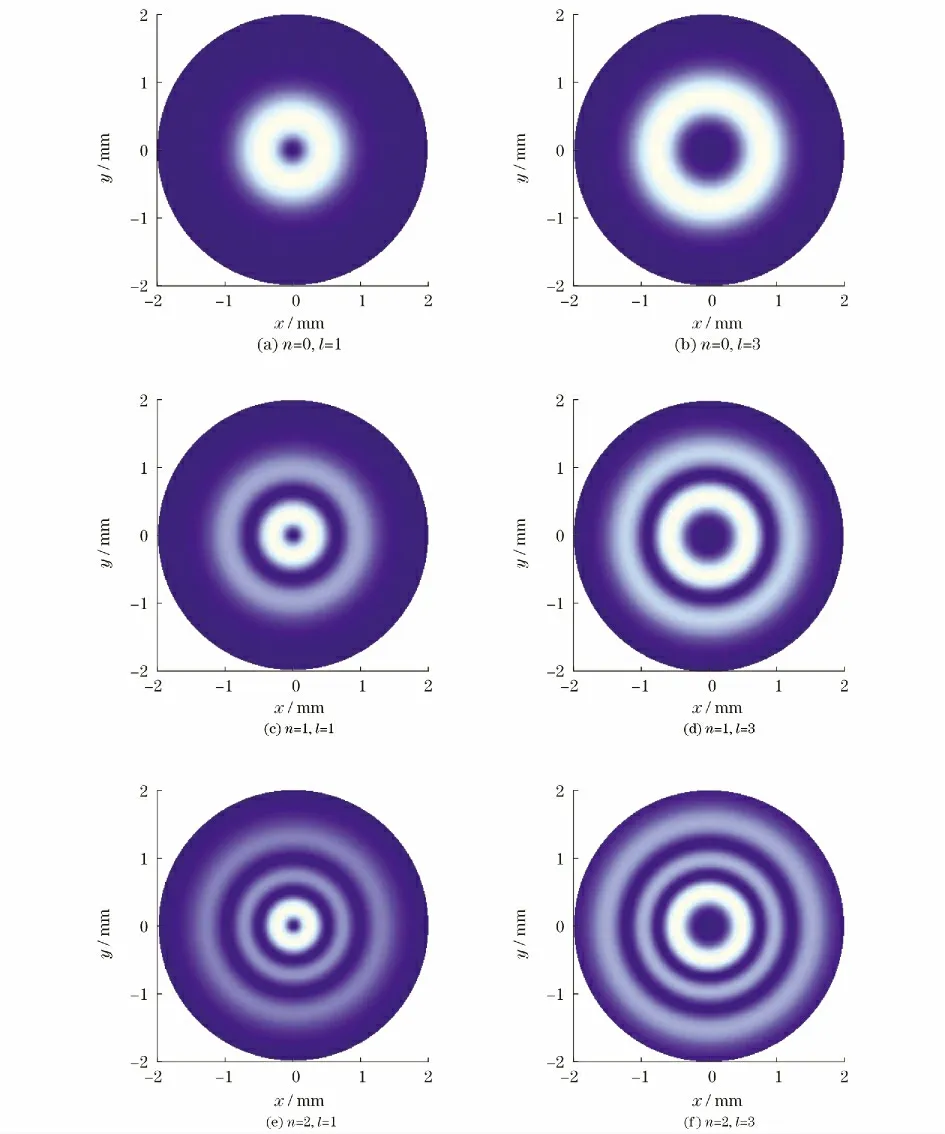
图2 z=1m 处不同阶数拉盖尔-高斯光束的强度分布Fig.2 Intensity distribution of Laguerre-Gaussian beams of different orders at z=1m
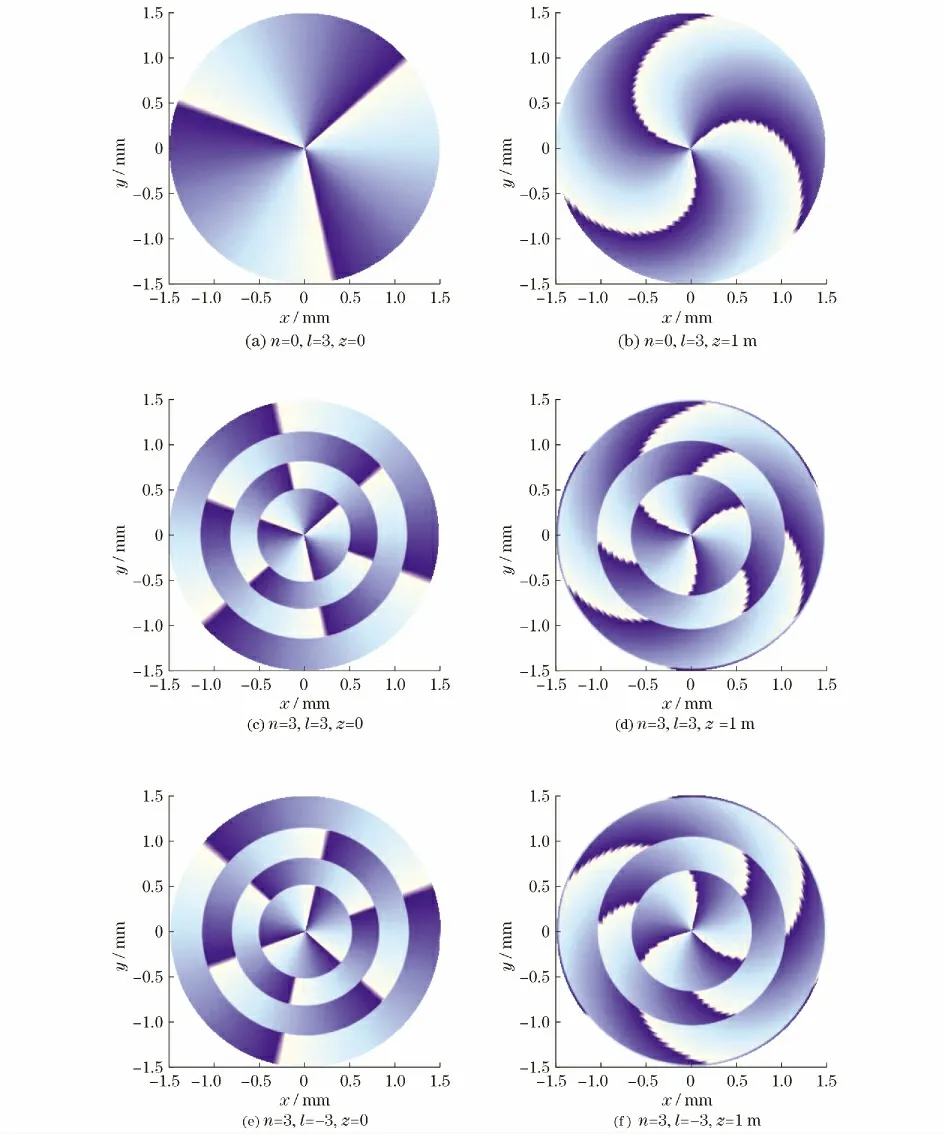
图3 z=0m 处和z=1m 处不同阶数拉盖尔-高斯光束的相位分布Fig.3 Phase distribution of Lagueere-Gaussian beams of different orders at z=0mand z=1m
3 结 论
得到式(15)等价于式(16)的结论是合理的,因为,式(16)是通过直接求解柱坐标系下傍轴波动方程获得的,而菲涅耳衍射公式(式(2))也源自于傍轴条件下的波动方程,由于理论的自洽性,同一个问题通过这两种方法得到的结果必然是等价的。因此,在探讨拉盖尔-高斯涡旋光束在自由空间的传播特性时,并不需要再作复杂的衍射积分,而可以直接使用拉盖尔-高斯光束的表达式。更为重要的是,本文虽然只推导了拉盖尔-高斯光束在自由空间的传播行为,但只要选取合适的A,B,C,D 系数,本文的研究方法适用于满足傍轴条件的任意光学系统。例如,只需将A=D=1,B=-1/f 代人式(5),经过相同的推导过程即可获得任意阶拉盖尔-高斯涡旋光束经过理想薄透镜的解析表达式。因此,本文的研究方法可应用于涡旋光束经过复杂光学系统时的研究。
[1]Gahagan K T,Swartzlander G A.Trapping of lowindex microparticles in an optical vortex[J].Journal of the Optical Society of America B,1998,15(2):524-534.
[2]Xu X Y,Kim K,Jhe W,et al.Efficient optical guiding of trapped cold atoms by a hollow laser beam[J].Physical Review A,2001,63(6):063401-063404.
[3]Song Y,Milam D,Hill W T.Long,narrow all-light atom guide[J].Optics Letters,1999,24(24):1805-1807.
[4]He X D,Xu P,Wang J,et al.Rotating single atoms in a ring lattice generated by a spatial light modulator[J].Optics Express,2009,17(23):21014-21021.
[5]Gao M W,Gao C Q,He X Y,et al.Rotation of particles by using the beam with orbital angular momentum[J].Acta Physica Sinica,2004,53(2):413-417.
[6]Gibson G,Courtial J,Padgett M J,et al.Free-space information transfer using light beams carrying orbital angular momentum[J].Optics Express,2004,12(22):5448-5456.
[7]Su Z K,Wang F Q,Lu Y Q,et al.Study on quantum cryptography using orbital angular momentum states of photons[J].Acta Physica Sinica,2008,57(5):3016-3021.
[8]Wang J,Yang J Y,Fazal I M,et al.Terabit free-space data transmission employing orbital angular momentum multiplexing[J].Nature Photonics,2012,6 (7):488-496.
[9]Willner A E,Wang J,Huang H.A different angle on light communications[J].Science,2012,337(6095):655-656.
[10]Liu Y D,Gao C Q,Gao M W,et al.Realizing high density optical data storage by using orbital angular momentum of light beam[J].Acta Physica Sinica,2007,56(2):854-858.
[11]Paterson C.Atmospheric turbulence and orbital angular momentum of single photons for optical communication[J].Physical Review Letters,2005,94(15):153901-153904.
[12]Rodenburg B,Lavery M P J,Malik M,et al.Influence of atmospheric turbulence on states of light carrying orbital angular momentum[J].Optics Letters,2012,37(17):3735-3737.
[13]Ding P F,Pu J X.Propagation of Laguerre-Gaussian vortex beam[J].Acta Physica Sinica,2011,60(9):0942041-0942045.
[14]Svelto O.Principles of lasers[M].4th ed.Beijing:World Publishing Corporation,2008:148-158.
[15]Abramochkin E G,Volostnikov V G.Generalized Gaussian beams[J].Journal of Optical A:Pure and Applied Optics,2004,6(5):S157-S161.
[16]Kogelnik H,Li T.Laser beams and resonators[J].Proceedings of the IEEE,1966,54(10):1312-1329.
