Elasto-plasticity and pore-pressure coupled analysis on the pullout behaviors of a plate anchor
2015-11-21CunHuFuPingGao
Cun Hu∗,Fu-Ping Gao
Key Laboratory for Mechanics in Fluid Solid Coupling Systems,Institute of Mechanics,Chinese Academy of Sciences,Beijing 100190,China
Elasto-plasticity and pore-pressure coupled analysis on the pullout behaviors of a plate anchor
Cun Hu∗,Fu-Ping Gao
Key Laboratory for Mechanics in Fluid Solid Coupling Systems,Institute of Mechanics,Chinese Academy of Sciences,Beijing 100190,China
A R T I C L E I N F O
Article history:
Received 23 October 2014
Accepted 9 January 2015
Available online 25 February 2015
Plate anchor
Bounding-surface plasticity model
Pore pressure
Coupled analysis
A numerical method is proposed for the elasto-plasticity and pore-pressure coupled analysis on the pulloutbehaviors ofa plate anchor.The bounding-surface plasticity(BSP)modelcombined with Biot’s consolidation theory is employed to simulate the cyclic loading induced elasto-plastic deformation of the soil skeleton and the accompanying generation/dissipation of the excess pore water pressure.The suction force generated around the anchor due to the cyclic variation of the pore water pressure has much effect on the pullout capacity of the plate anchor.The calculated pullout capacity with the proposed method(i.e.,the coupled analysis)gets lower than that with the conventional total stress analysis for the case of long-term sustained loading,but slightly higher for the case of short-term monotonic loading.The cyclic loading induced accumulation of pore water pressure may result in an obvious decrease of the stiffness of the soil-plate anchor system.
©2015 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license(http:// creativecommons.org/licenses/by-nc-nd/4.0/).
The current evaluation for the pullout capacity of plate anchors in the seabed is usually on the assumption ofundrained conditions,which could not capture the effect of cyclic pore pressure[1].The cyclic loading onto the plate anchor may soften and remould the neighboring soiland even further generate pore pressures,thereby both the strength and stiffness of the soil would be changed significantly[2].Moreover,the dissipation of the pore pressure under the long-term sustained loading may further bring the regaining of the stiffness and recovery of the strength[3].Therefore,an accurate evaluation of the strength and stiffness of the soil within an effective stress framework is necessary for determining the bearing capacity of a plate anchor.
The undrained ultimate pullout capacity of the plate anchor has been studied experimentally[4]and theoretically[5],in which the total stress analysis method was adopted with neglecting the interaction between the pore water and the soil skeleton throughout the life time of the plate anchor.Previous efforts on the cyclic pullout behavior of the plate anchor were mainly physical modeling[6,7],where the pore pressures were rarely obtained.Similar coupled analyses on the pipeline are available,however,in which the soil was assumed as a porous elastic rather than an elasto-plastic media in the prediction of the pore pressure dissipation[8].It would be erroneous if the plastic deformation of the soil is not taken into account in the process of the plate anchor being pulled out.Chatterjee et al.[9]adopted the modified cam-clay plasticity(MCC)soil model to study the effects of the dissipation and generation of pore water pressure on the breakout resistance of the embedded pipeline.The MCC model is not capable of describing the cyclic behavior of soils.
In this study,a numerical method for the elasto-plasticity and pore-pressure coupled analysis on the pullout behaviors of a plate anchor is proposed,in which the bounding-surface plasticity(BSP)model[10,11]combined with the Biot’s consolidation theory is employed to model the cyclic loading induced elastoplastic deformation ofthe soilskeleton and the accompanying generation/dissipation of the excess pore water pressure.The finite element mesh of a plane strain model and its boundary conditions are schematically shown in Fig.1.As the drag force is vertically loaded onto the plate anchor,the symmetry condition is used with a vertical axis passing through the center of the plate anchor.The main focus here is on elasto-plastic deformation ofthe soilskeleton and the development of the pore water pressure.The plate anchor model is treated as a rigid body,which is fully bonded with soil element.
In this coupled analysis,the equilibrium equation of the soil element,the effective stress principle,the stress-strain equation for the soil skeleton and the continuity equation of the water flow should be satisfied.The main governing equations are given as follows:
(1)BSP model to control the elasto-plasticity deformation of the soil skeleton


Table 1Soil parameters for the BSP model.
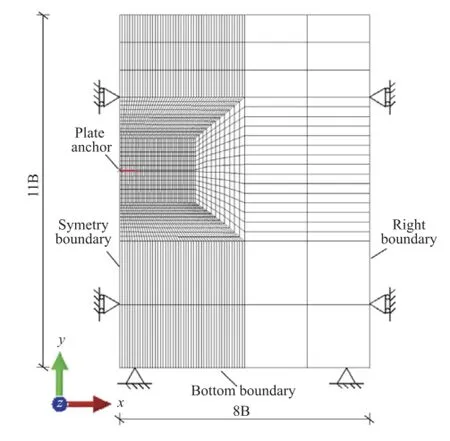
Fig.1.Schematic of finite element mesh of a plane strain model and the boundary conditions.
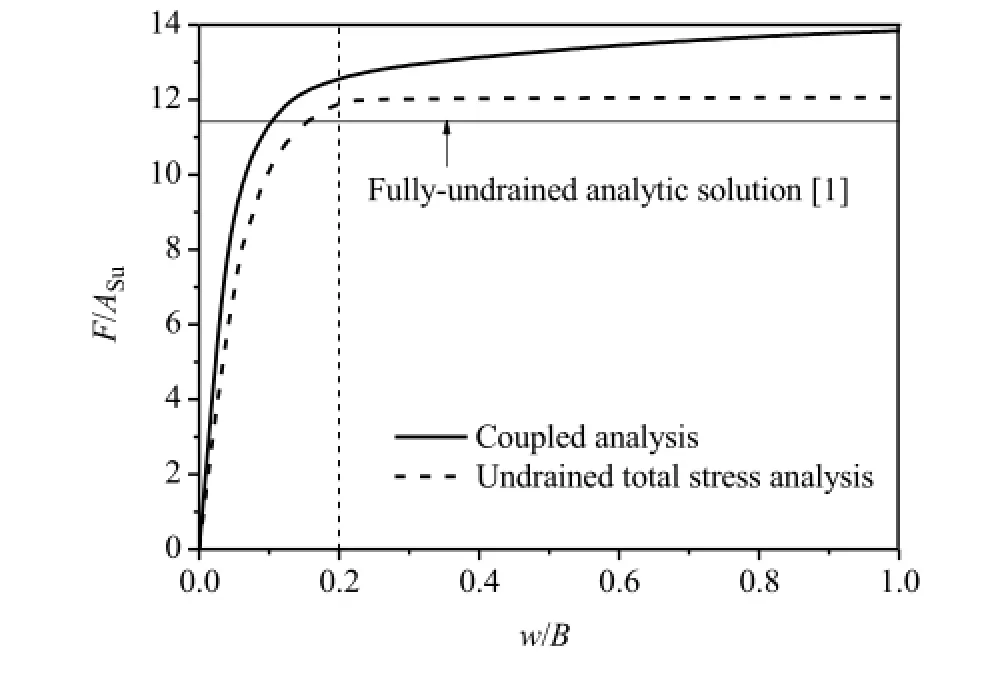
Fig.2.Normalized load-displacement curve.
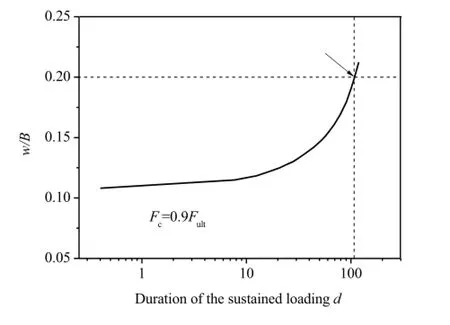
Fig.3.Normalized displacement vs the loading time.
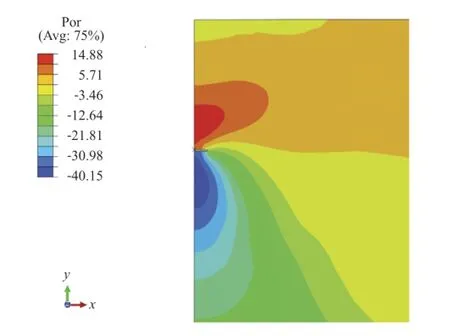
Fig.4.The generation of the pore water pressure.

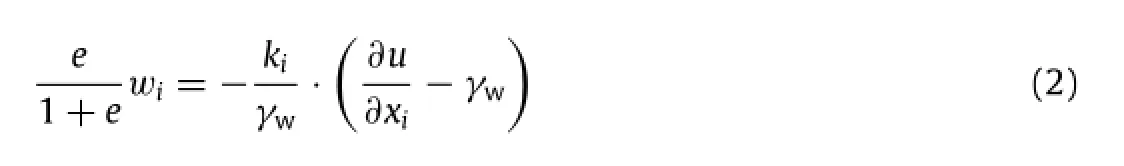
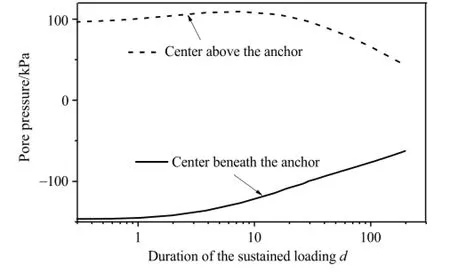
Fig.5.The dissipation of the pore water pressure.
where e is the void ratio,withe fluid velocity,kiis the permeability of the soil,xiis the position,γwis the specific weight of the water,and u is the pore water pressure.The advantage ofcoupled analyses is its capability for evaluating the effects of the dissipation of pore pressure on the ultimate pullout capacity,and the effects of the generation of pore water pressure on the weakening of the shear strength.
A uniform pressure of 110 kPa is applied on the surface of the soil to alleviate numerical problems associated with the very low shear strength of the soil at the mudline and minimize the variation of soil properties with depth[9].Similar to the MCC model,the initial shear strength also depends on the pre-consolidation pressure p0in the BSP model.Parameters of the BSP model include the criticalstate one and hardening modulus parameters(see Table 1),which are typical properties for a Kaolin clay.For plane strain conditions,the undrained shear strength can be expressed as follows[9]
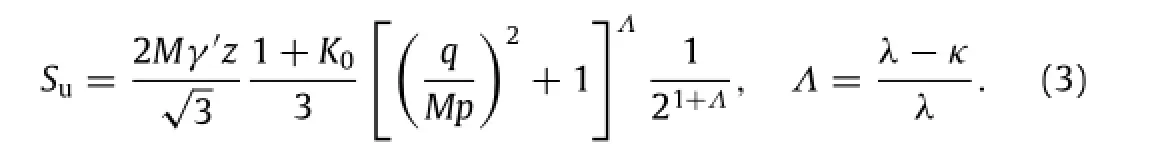
Thus,the normalization of the pullout capacity factor can be more straightforward.The undrained total stress analysis is further performed using the elastic perfectly plastic modelwith the Mises failure criterion,which is an approximation to Tresca failure criterion and provides a better fit to the hexagon in a deviatoric stress plane of the Tresca criterion[12].The parameters of the elastic perfectly plastic model can be determined with
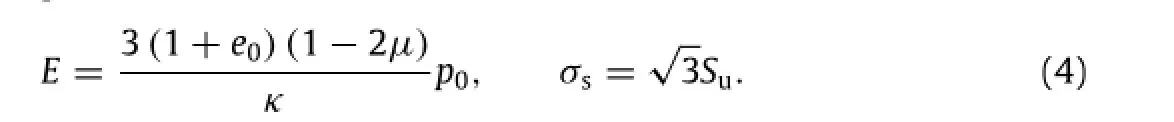
Figure 2 shows the numericalresults for the ultimate pulloutresponse ofa plate anchorcalculated with differentmethods,including the fully-undrained analytical solution,undrained total stress analysis,and the present coupled analysis.Note that the pull velocity v is set as 0.06×10-3m/s in the coupled analysis.The ultimate capacity factor is chosen at a value of w/B=0.2,which has been widely used as a failure criterion.It is indicated that the ultimate capacity factor obtained by the coupled analysis is slightly higher than that by the analytical solution[7]and that with the assumption ofthe fully undrained condition.This is due to that,in the coupled analysis,the soil is normally not fully undrained,and the shear strength would be higher correspondingly.When the nondimensional velocity v B/cv≥100(c v is the consolidation coefficient),the soil response can be assumed to be undrained[9].Inthis simulation,v B/cv=53.4,thus partial dissipation of the pore pressure occurs.

Fig.6.Cyclic responses of the seabed-plate anchor system.
To further investigate the effect of the dissipation of the pore pressure,a long-term sustained loading with the amplitude of Fc=0.95 Fult(Fultis the ultimate pullout capacity)is applied on the plate anchor in 12 h,then kept constant.With loading time increasing,the plate anchor displacement(see Fig.3)and the pore pressure dissipation occurs(see Figs.4 and 5).As shown in Fig.5,the dissipation of the pore pressure reduces the suction force at the bottom of the plate anchor.As the sustained uplift load keeps constant,the plate anchor moves upwards accordingly due to the force unbalance.The movement of the plate anchor may further induce the generation of the pore pressure in the soil and the change of suction force onto the structure.Meanwhile,the newly generated pore pressure would be dissipating with time again.An equivalent reduction of the positive excess pore pressure exists at the top of the anchor,so the movement of the plate anchor would be updated again until reaching the failure state.The allowable duration of the sustained loading can be determined from Fig.3. Under the sustained loading of the amplitude of 0.95 Fult,the plate anchor can last 110 days without failure.Therefore,in the evaluation of the undrained ultimate pullout capacity,it might be dangerous when a long-term sustained loading exists,such as the seasonalcurrent loops,throughout the lifetime of the plate anchor.
Figure 6(a)shows the typical development of the pore water pressure at the point above the center of the top surface of the plate anchor under a one-way cyclic loading(i.e.,a mean load Qmcombined with a superimposed cyclic load Qcyc).The accumulation of pore water pressure increases rapidly(see Fig.6(a)),which implies the decrease both in effective stress(see Fig.6(b))and in shear strength of the soil.The corresponding displacement history is given in Fig.6(c).It is indicated that for the cyclic loading with a constant amplitude,the displacement increment per cycle increases with the loading cycles,which means that the cyclic stiffness decreases.Actually,the sum of Qmand Qcycis still lower than the ultimate pullout capacity,the failure state is reached in a few cycles,indicating that the cyclic nature of loading may reduce the soil strength and stiffness.That is,the remoulding effect could be dominant in the process of the plate anchor being pulled out under the cyclic loading.
This work was supported by the National Natural Science Foundation of China(51309213)and the 973 program of China(2014CB046200).
[1]Det Norshke Veritas,Design and installation of fluke anchors in clay.DNV RPE302,2002.
[2]M.S.Hodder,D.J.White,M.J.Cassidy,An effective stress framework for the variation in penetration resistance due to episodes of remoulding and reconsolidation,Geotechnique 63(2013)30-43.
[3]E.C.Cluckey,J.S.Templeton,M.F.Randolph,Suction caisson response under sustained loop current loads,in:Offshore Technology Conference,Houston,OTC16843,2004.
[4]B.Wilde,Programof Centrifuge and Field Tests on the Suction Embedded Plate Anchor,Report to SEPLA JIP,Inter Moor Inc,Houston,2005.
[5]R.S.Merifield,S.W.Sloan,H.S.Yu,Stability of plate anchors in undrained clay,Geotechnique 51(2001)141-153.
[6]L.Yu,Q.Zhou,J.Liu,Experimental study on the strain softening behavior of plate anchors in clay under cyclic loading,in:Proceedings of the ASME 2014 33rd International Conference on Ocean,Offshore and Arctic Engineering,San Francisco,June 8-13,2014.
[7]S.P.Singh,S.V.Ramaswamy,Influence of frequency on the behaviour of plate anchors subjected to cyclic loading,Mar.Georesources Geotechnol.26(2008)36-50.
[8]K.Krost,S.M.Gourvenec,D.J.White,Consolidation around partially embedded seabed pipelines,Geotechnique 61(2011)167-173.
[9]S.Chatterjee,Y.Yan,M.F.Randolph,D.J.White,Coupled consolidation analysis of pipe-soil interactions,Can.Geotech.J.50(2013)609-619.
[10]C.Hu,H.X.Liu,W.Huang,Anisotropic bounding-surface plasticity model for the cyclic shakedown and degradation of saturated clay,Comput.Geotech.44(2012)34-47.
[11]C.Hu,H.X.Liu,Implicit and explicit integration schemes in the anisotropic bounding surface plasticity model for cyclic behaviors of saturated clay,Comput.Geotech.55(2014)27-41.
[12]D.M.Potts,L.Zdravkovic,Finite Element Analysis in GeotechnicalEngineering: Theory,Thomas Telford Publishing,London,1999.
∗Corresponding author.
E-mail addresses:hucun@imech.ac.cn(C.Hu),fpgao@imech.ac.cn(F.-P.Gao).
*This article belongs to the Solid Mechanics
杂志排行
Theoretical & Applied Mechanics Letters的其它文章
- Failure mechanisms of a spudcan penetrating next to an existing footprint
- Difficulties and measures of driving super long piles in Bohai Gulf
- Assessment of pipeline stability in the Gulf of Mexico during hurricanes using dynamic analysis
- Long-term dynamic behavior of monopile supported offshore wind turbines in sand
- Coupling model for waves propagating over a porous seabed
- Experimental study on the stability of plate anchors in clay under cyclic loading
