Coupling model for waves propagating over a porous seabed

C.C.Lio，Z.Lin，Y.Guo，D.-S.Jeng

aDepartment of Civil Engineering，Shanghai Jiao Tong University，Shanghai 200240，China

bSchool of Engineering，University of Aberdeen，Aberdeen，UK

cGriffith School of Engineering，Griffith University Gold Coast Campus，Queensland，QLD 4222，Australia

dSchool of Engineering，University of Bradford，BD7 1DP，UK

Coupling model for waves propagating over a porous seabed

C.C.Liaoa，Z.Linb，Y.Guod，D.-S.Jengc，∗

aDepartment of Civil Engineering，Shanghai Jiao Tong University，Shanghai 200240，China

bSchool of Engineering，University of Aberdeen，Aberdeen，UK

cGriffith School of Engineering，Griffith University Gold Coast Campus，Queensland，QLD 4222，Australia

dSchool of Engineering，University of Bradford，BD7 1DP，UK

A R T I C L E I N F O

Article history:

Received 23 October 2014

Accepted 29 December 2014

Available online 11 March 2015

Coupled model

Momentum source

Internal wave-maker

Seabed response

Pore pressure

Liquefaction

The wave-seabed interaction issue is of great importance for the design of foundation around marine infrastructures.Most previous investigations for such a problem have been limited to uncoupled or oneway coupled methods connecting two separated wave and seabed sub models with the continuity of pressures at the seabed surface.In this study，a strongly coupled model was proposed to realize both wave and seabed processes in a same program and to calculate the wave fields and seabed response simultaneously.The information between wave fields and seabed fields were strongly shared and thus results in a more profound investigation of the mechanism of the wave-seabed interaction.In this letter，the wave and seabed models were validated with previous experimental tests.Then，a set of application of present model were discussed in prediction of the wave-induced seabed response.Numerical results show the wave-induced liquefaction area of coupled model is smaller than that of uncoupled model.

©2015 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license（http:// creativecommons.org/licenses/by-nc-nd/4.0/）.

The wave-seabed interaction problems have been extensively studied by marine geotechnical engineers in recent years.One of reasons for this growing interest is that numerous marine installations have been reported to be damaged by wave-induced seabed instability［1］，rather than by construction or material failure.Most existing studies for the phenomenon of wave-seabed interactions have been limited to either uncoupled or one-way coupling approach，which may not represent the real process in the marine environments.Therefore，it is necessary to develop a coupling model to provide better prediction of the wave-induced soil response in a porous seabed.

In this study，both oscillatory and residual mechanisms of the wave-induced pore pressure are considered.The oscillatory mechanism was modeled by the Biot consolidation theory［2］，while the residual mechanism was modeled by plastic theory under cyclic loading.The existing plastic model for residual mechanism［3］will be extended to two-dimensional before we coupled it with the wave model.The wave process was simulated using a momentum source function.Both the wave process and seabed process were built in COMSOL Multiphysics environments. The advantage of this coupled model is to allow us to see the effects of both components（wave and seabed）on wave-seabed interaction，unlikely previous one-way integrated models［4］.To the authors’best knowledge，this paper may be the firstone solving the wave field and seabed response simultaneously in this field.

Two sub-modules are included in the proposed coupled wave-seabed model:wave generation module and seabed module. The wave module is established for generating waves and describing their propagation in a viscous fluid.The seabed module is used to determine the seabed responses to the waves，including the pore pressure，soildisplacements，and effective stresses.Unlike any previous one-way integrating model，these two sub-modules are strongly coupled in COMSOL Multiphysics，in which wave and seabed model are simultaneously calculated.

In the wave model，the flow field inside and outside of the porous media is determined by solving the revised Reynoldsaveraged Navier-Stokes（RANS）equations，which are derived by integrating the momentum source term over the traditional RANS equations.The flow motion of an incompressible fluid can be described by Navier-Stokes equations

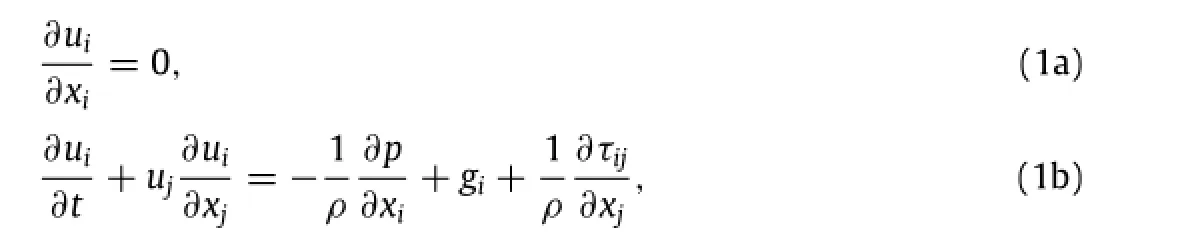
where i，j=1，2，3 are for three-dimensional flows，uiis the i-th component of the velocity vector，ρis density，p is pressure，giis the j-th component of the gravitational acceleration，andτijis the element of viscous stress tensor.

Equation（1a）represents the conservation of mass，which has been reduced to the requirement of zero divergence of velocity vector for incompressible fluids.Equation（1b）denotes the conservation of momentum.Generally speaking，there are several options to numerically generate a required wave via an internal wave-maker.One is to add a mass source term in the mass conservation equation（1a）.Another is to introduce a momentum source term in the momentum conservation（1b）.One can also use both the mass and momentum sources to generate a train of wave.Theoretically，this mass/momentum source could be a point source，a line source，or a finite volume source［5］.In this study，we used an internal wave-maker method for generating essentially directional waves in a two-dimensional domain using a momentum source function of the RANS equation［6］.More detailed information for wave generations，readers can refer to Ref.［6］.

In the seabed model，the wave-induced pressure and stress oscillations，denoted by Pb（x，t）andτb（x，t），that further induce the pore pressure p at a generic point in the soil bed to vary with time from the hydrostatic value ps.Let pe=p-psdenote the wave-induced excess pore pressure at a point at the time（t）.As suggested in Ref.［3］，peconsists of two components，i.e.，

The poro-elastoplastic theory was adopted in the present study intending to solve the wave-induced pore pressure，which consists of two components:elastic part for oscillatory pore pressure and plastic part for residual pore pressure.More detailed information，readers can refer Ref.［7］for oscillatory mechanism and Ref.［3］for residual mechanism.

To solve the flow and seabed fields，severalboundary conditions are required.As to the wave module，first，the upper boundary of air layer in wave-module is set as a pressure outlet，where the pressure can flow in and out without any constrain.Second，continuity of pressure and fluid displacement is applied at the air/water interface.Then，at the bottomboundary ofwater domain，the displacement of the water particles is equal to that of the seabed surface.

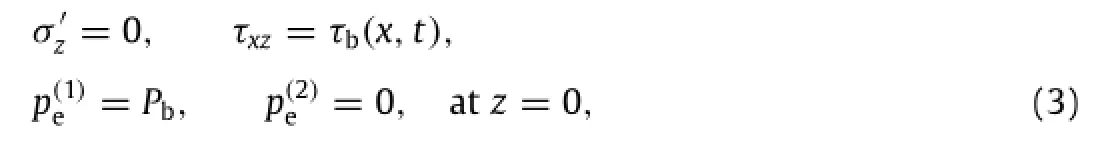
where Pb（x，t）andτb（x，t）are the dynamic wave pressures and bottomwave shear stresses atthe seabed surface，respectively，and both can be obtained fromthe wave modeloutlined in Eqs.（1a）and（1b）.

Second，for the soil resting on an impermeable rigid bottom，zero displacements are assumed.Furthermore，no vertical flow occurs at the horizontal bottom，i.e.，

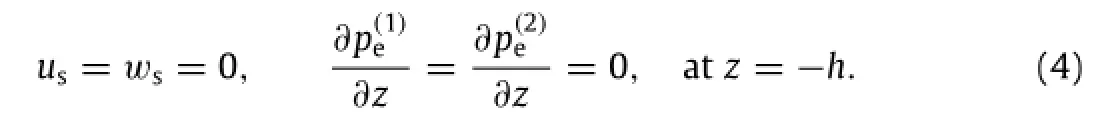
In coupling process，wave module is responsible for the simulation of the wave propagation and determines the pressure and stress acting on the seabed surface.Laminar two-phase（air and water）flow theory with level set method and moving mesh method are used to model the fluid flow of two different，immiscible fluids，when the exact position of the interface is of interest.The interface position is tracked by a moving mesh，with boundary conditions that account for surface tension and wetting，as well as mass transport across the interface.The level set method tracks the fluid-fluid interface using an auxiliary function on a fixed mesh.Since the displacement of seabed surface from seabed module will definitely affect the flow field in the wave module，the authors used the moving mesh method to track the timedependent displacement of seabed surface as well.

The seabed is modeled with the PDE interface to solve all the equations describing the elastoplastic soil.Both the oscillatory pore pressure and residual pore pressure were considered in the present theory.The pressure/force acting on the seabed were determined by the wave module and were provided to the seabed module to calculate the dynamic response of the seabed including the displacements，pore pressure and the effective stresses. Meanwhile，the information of seabed will in return feed backed to the wave module to adjust the computation of flow field.Within a same time step，the information of seabed response and the flow field were strongly coupled and shared without any time lag.

In this letter，we re-produced the wave and seabed models within COMSOL Multiphysics environments.The main contribution ofthis study lies on the coupling two models through COMSOL，which is a challenge with the previous models.

Two kinds of seabed response will be verified here:oscillatory mechanism and residual mechanism.The oscillatory mechanism will be compared with a one-dimensional compressive test conducted by Liu and Jeng［8］.Then，the residual mechanism will be compared with the centrifuge tests under progressive wave and standing wave，seperatively.

It should be noted that in their experiment，only the onedimensional cylinder model facility was used.Thus，the wave length should be revised as infinite in the present model.Other input data used is also included in Fig.1.As shown in the figure，the present model overall agrees with the one-dimensional experimental data，indicating a promising prediction of oscillatory pore pressure by present coupling model.

Fig.1.Comparison with one-dimensional experimental data［8］.

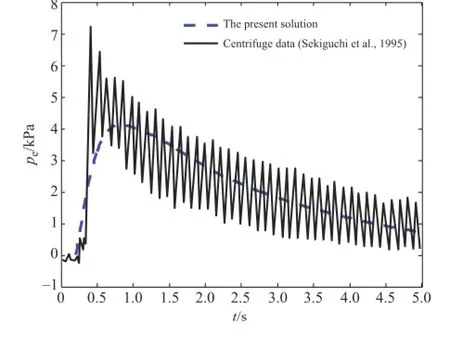
Fig.2.Comparison with centrifuge test data［9］.

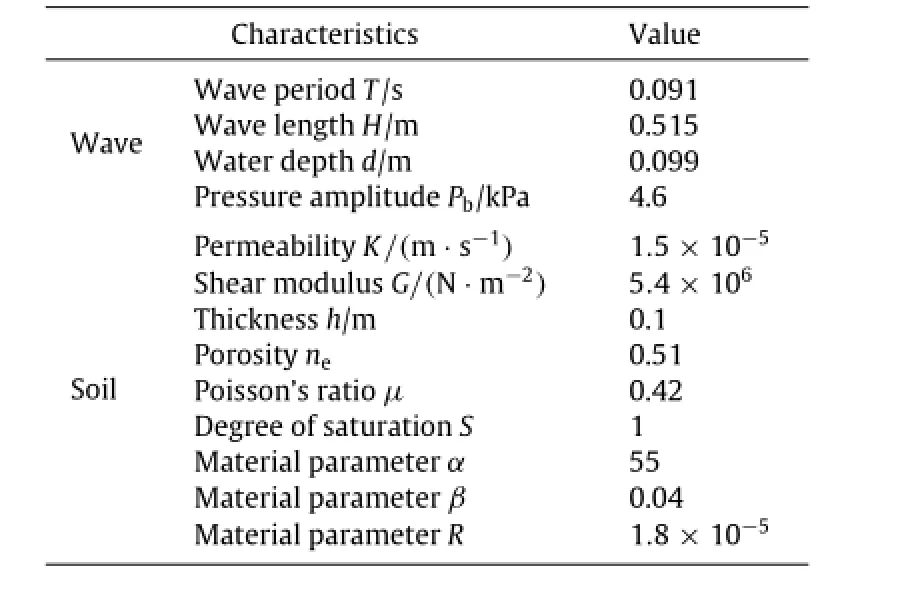
Table 1Details of centrifuge wave tests on loose deposits of sand［3］.

The first centrifugal standing wave tests were conducted by Sekiguchi et al.［9］using a balanced-beam centrifuge in order to investigate the wave-induced instability of horizontal deposits of sand.In their study，standing waves were formed when the fluid was excited at a frequency f=8.8 Hz under a steady-state centrifugal acceleration of 50g，with a fluid depth d=47 mm. These conditions correspond to d=2.35 m and f=0.176 Hz in the ordinary gravitational conditions.The amplitude of the input pressure fluctuation was p0=1.7 kPa.The plastic parameter βis 1.4（corresponding to the parameter‘‘α’’in Ref.［9］）.Other parameters wereα=55，R=1.8×10-5，and porosity ns=0.5. More details can be found in Ref.［9］.The excess pore pressure response measured in the centrifuge test is now compared with the prediction from the present poro-elastoplastic solution.In this comparison，the authors only choose the pore pressure-time histories for elevation z/h=-0.25.As shown in Fig.2，the predicted maximum pore pressure is slightly smaller than that of the centrifugal test.Except this，the prediction overall agrees with the centrifugal data under standing waves.

Another centrifugal progressive-wave tests were conducted on beds of fine-grained sands by Sassa and Sekiguchi［3］.The experiment was concerned with loose deposits of Leighton Buzzard sand under a centrifugal acceleration of 50g.Details of the centrifuge wave tests are summarized in Table 1.Figure 3 shows that the predicted results capture the essential features of the measured results with respect to the residual pore pressure.Both the maximum pore pressure and the build-up（and dissipation）of the pore pressure can be predicted well.Overall，the present model works well in trend with the measured pore pressure under progressive waves.

In this letter，two issues will be discussed in detail with the coupling model:the effect of plasticity on seabed response and the influence ofcoupling on wave-induced liquefaction.The input data that may be used in this section is summarized in Table 2.

Compared to the elastic soil model，the soil plasticity may have some different effects on the full soil behavior.To have a clear understanding of the influence of soil plasticity，a series of numerical studies is undertaken in this case.To demonstrate the effects of soil plasticity，the soil depth is chosen as infinite in this example.The input data is shown in Table 2.As illustrated in Fig.4，the difference between elastic model and elastoplastic model can not always be ignored.It clearly shows that the pore pressuregap between these two models enhances when the loading cycles increases.

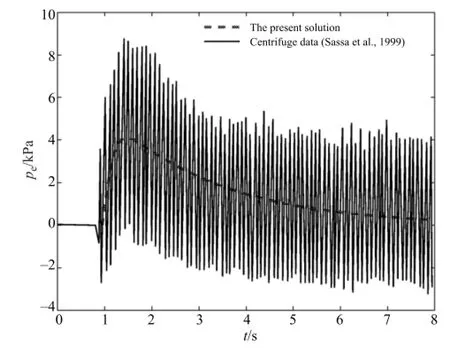
Fig.3.Comparison with centrifugal test data［3］.

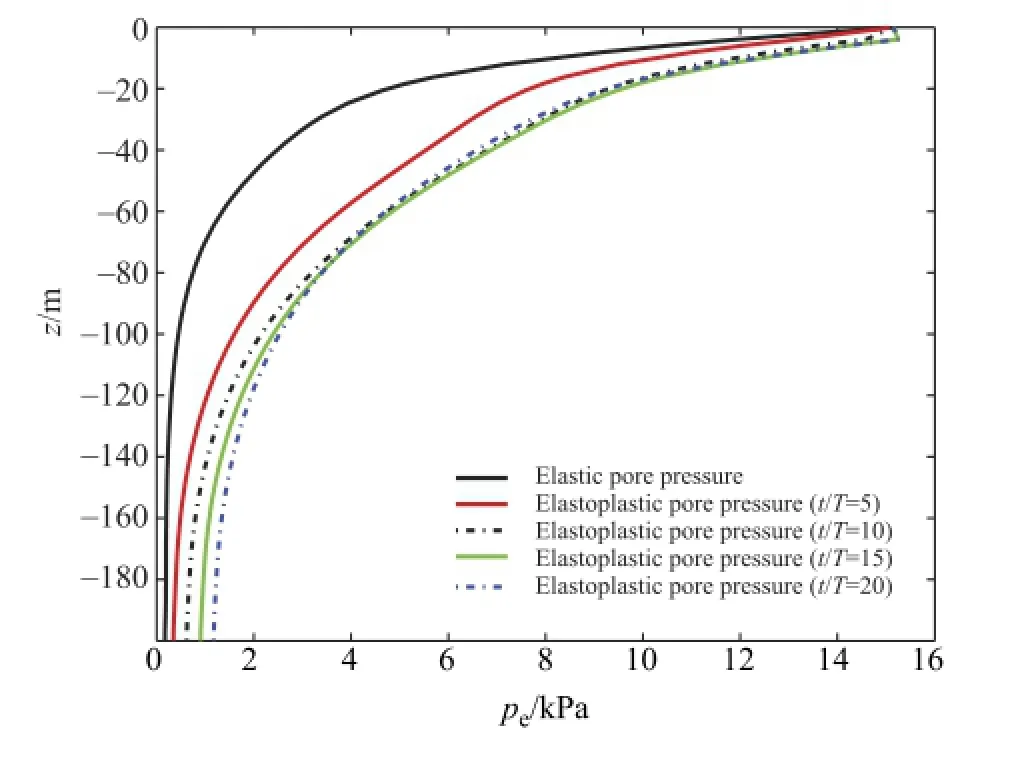
Fig.4.Vertical distribution of wave-induced pore pressure between elastic and elastoplastic models.

Table 2Input data for application of present model.

To examine the difference between the coupled and uncoupled model on wave-induced liquefaction，the development of waveinduced liquefaction areas are presented in Fig.5.To control other variables（like plasticity）thatmay affect the liquefaction area，both models are only applied the elastic theory to modeling the seabed response.Other parameters are the same illustrated in Table 2. As shown in Fig.5，it can be concluded that the wave-induced liquefaction area in coupled model is small than that in the uncoupling model.Considering that the displacement of the seabed surface may affect the flow field from the wave generation model，which is not considered in previous one-way model，the water pressure acting on the seabed will decrease by the seabed motion. Therefore the soil response may be slightly small than the uncoupled model，and so does the liquefaction area.

Fig.5.Comparison of liquefaction zone between coupled and uncoupled models.

Acknowledgment

This work was supported by the National Natural Science Foundation of China（41176073）.

［1］B.M.Sumer，J.Fredsøe，The Mechanism of Scour in the Marine Environment，World Scientific Pub.，New Jersey，2002.

［2］M.A.Biot，General theory of three-dimensional consolidation，J.Appl.Phys.12（1941）155-164.

［3］S.Sassa，H.Sekiguchi，Wave-induced liquefaction ofbedsofsand in a centrifuge，Géotechnique 49（1999）621-638.

［4］D.S.Jeng，J.H.Ye，J.S.Zhang，P.F.Liu，An integrated model for the waveinduced seabed response around marine structures:Model verifications and applications，Coast.Eng.72（2013）1-19.

［5］P.Lin，P.L.F.Liu，Internal wave-maker for Navier-Stokes equations models，J. Waterway，Port，Coast.Ocean Eng.，ASCE 125（1999）207-217.

［6］J.Choi，S.B.Yoon，Numerical simulations using momentum source wave-maker applied to RANS equation model，Coast.Eng.56（2009）1043-1060.

［7］D.S.Jeng，Porous Models for Wave-seabed Interactions，Spring，Berlin，2013.

［8］B.Liu，D.S.Jeng，The Laboratory study for pore pressure in sandy bed under wave loading，in:The 23rd International Offshore and Polar Engineering Conference（ISOPE2013），Anchorage，Alaska，2013.

［9］H.Sekiguchi，K.Kita，O.Okamoto，Response of poro-elastoplastic beds to standing waves，Soils Found.35（1995）31-42.

∗Corresponding author.

E-mail address:d.jeng@griffith.edu.au（D.-S.Jeng）.

*This article belongs to the Solid Mechanics