图上低频信号谱域变换中的边权重优化设计

史雪松，冯 辉，杨 涛，胡 波，2

（1.复旦大学 电子工程系，上海 200433；2.复旦大学 电磁波信息科学教育部重点实验室，上海 200433）

网络化数据处理的需求出现在无线传感器网络、移动通信、互联网大数据等多个研究领域.与等间隔采样的时域或者空域信号相比，网络中的数据位置分布不规则，数据之间存在拓扑联系，因此无法直接采用传统的信号处理工具进行分析.在近两年的研究中，图上信号处理理论［1］和相关应用方兴未艾，这些研究中将网络抽象为图，将网络中的数据看作分布于图中各节点上的信号，以传统数字信号处理理论中的方法为参照，发展出图上信号的采样和滤波理论［2－5］.根据图上信号处理理论，图上信号可以通过图上傅里叶变换投影到谱域，从而得到信号在图上的频谱，而投影的方向取决于图中节点间的边连接关系和边的权重.图上信号的频谱与传统数字信号的频谱有相似的物理意义，直观上，信号频谱的低频成分较强说明信号在图上分布较为平滑，即图中相邻的节点上具有较为接近的信号值，而高频成分较强说明信号在图上变化较为剧烈.

图上信号处理理论催生了一批用于网络化数据的降噪［6］、压缩［3］、异常检测［7］等应用的新算法.这类算法通常假设图的拓扑体现了数据的某些内在结构，从而使得无噪声、无异常的信号在图上分布较为平滑，即其频谱主要分布于图谱的低频部分［8］.然而，图上信号的频谱分布不仅取决于图的拓扑，还受到图中边权重的影响.绝大多数网络化数据处理应用中并没有图的边权重的先验定义，因此边权重的优化设计是当下值得研究的课题.

现有的关于图上信号处理的文献中针对图中边的权重设计的研究较为缺乏，绝大多数文献或跳过这一步骤，或将其认为是经验性的，简单地选用一些未经论证的权重计算方法［1］.另有少量研究针对特定应用中的权重设计问题进行了分析，但其结论缺乏通用性［9－13］.在网络一致性算法相关的应用中，对图的边权重的优化可以表述为对加权图的拉普拉斯矩阵的某些特征值的优化［10－11］.Shafi等人提出了一种通用性的优化图的拉普拉斯矩阵的特征值的方法［14］，可以使构造出的边权重满足对拉普拉斯矩阵的任意多个特征值进行的约束.然而，相比于拉普拉斯矩阵的特征值，图上的信号处理研究中更关注拉普拉斯矩阵的特征向量，因为特征向量决定了信号从点域向谱域投影的方向.针对图上信号处理的通用性权重设计方法的研究非常少，最近由Dong等人提出的一种基于信号平滑性假设的权重优化算法［8］，适用于在无结构信息的数据集中构造加权图.

网络化数据是有网络结构信息的数据集，在这类场景中构造的图的拓扑必须保持网络拓扑不变.本文即研究图上低频信号在拓扑约束情况下图的边权重设计问题.首先，对图上信号的低频程度提出一种量化指标，并证明其与图上的平滑性在数学上等价.然后将拓扑约束下的边权重设计问题描述为最优化问题，使信号在设计得到的图上具有最显著的低频特性.另外，面对分布式处理的实际需求，本文设计了分布式权重优化（Distributed Optimal Weighting，DOW）算法.通过DOW 算法，网络中的每个节点仅需与相邻节点进行少量通信，即可通过计算获知自己与每个相邻节点间的最优边权重.

1 图上信号的谱域变换

考虑包含N 个节点的无向加权连通图G，其加权的邻接矩阵为对称阵W ∈ℝN×N，对任意i，j＝1，2，…，N，Wij＞0代表节点i和节点j 之间存在一条权重为Wij的边连接，Wij＝0代表节点i和节点j 之间不存在边连接.图G 的拉普拉斯矩阵L 定义为

其中1 表示元素全部为1的列向量，diag（W1）表示以向量W1 中的元素为对角元的对角阵.L 的特征值分解为

其中Λ＝diag（λ1，λ2，…，λN）为对角阵，其对角线元素构成图G 的谱.注意对于权重非负的无向加权图，其谱中的所有元素均为非负实数，且其中0的个数等于图的连通分支数［1］.不失一般性，假设图G 的谱是已排序的：0＝λ1＜λ2≤…≤λN.矩阵U＝（u1，u2，…，uN）中包含了L 的特征向量，且具有标准正交性：

图G 上的信号为关联到图的节点上的一组数据，以向量x∈ℝN表示.对任意i＝1，2，…，N，xi代表节点i上的数据.根据图上傅里叶变换［1］，信号x的频谱为

2 低频信号的谱域特征

许多图上信号处理应用，如降噪、数据压缩、异常检测等，要求信号的频谱的能量主要集中在低频区域［9，15］，以便于在谱域对信号和噪声进行区分.因此针对这些应用，在构造图的过程中，应当优化边权重使得信号在构造的图上尽可能呈现低频特性.本节对低频特性进行数学上的定量描述.

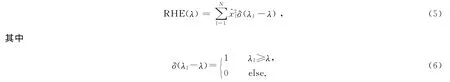
图1给出了一个包含10个节点的图上信号的能量分布的例子.

要使信号尽可能呈现低频特性，应当使信号的残留高频能量在每个频率上的值都尽可能小.为了量化这一标准，定义整体RHE为RHE在整个频谱上的积分，如图1（b）中的阴影部分所示.整体RHE越小，说明信号在图上越集中在低频段.定理1 给出了通过拉普拉斯矩阵计算信号的整体RHE 的方法.

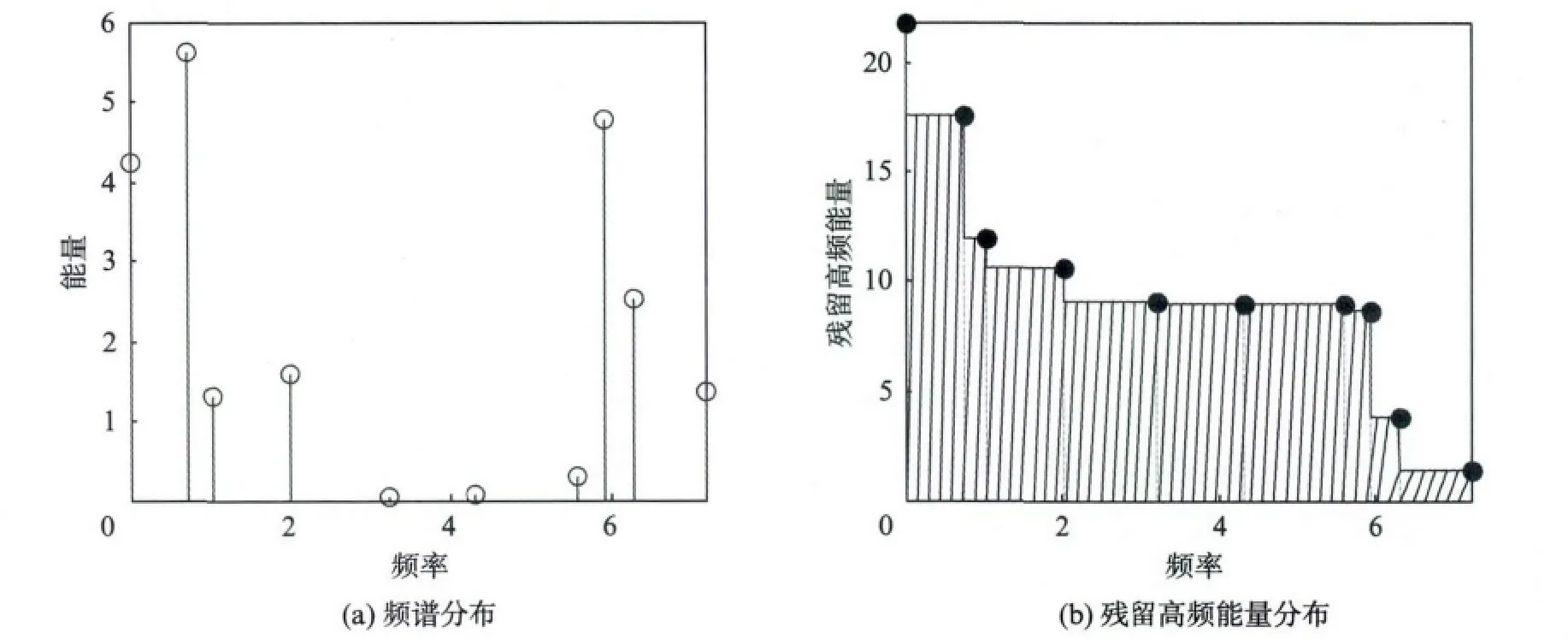
图1 图上信号的能量分布示例Fig.1 Example of the energy distribution of a graph signal

定理1 若图的拉普拉斯矩阵为L，则图上信号x的整体RHE为

证 根据式（5），可得

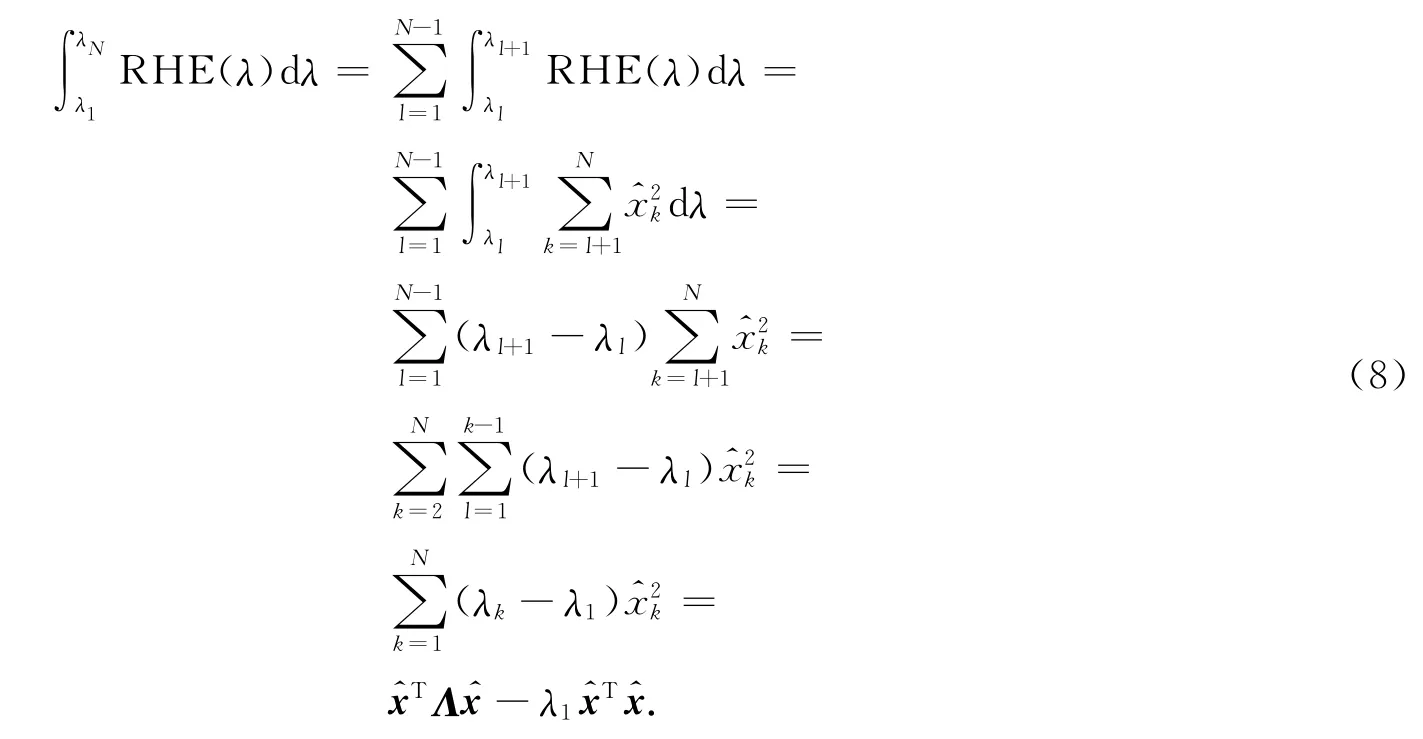
将式（4）和λ1＝0代入式（8），得到

又由式（2），得到式（7）.

定理1证明图上信号的整体RHE等于其针对拉普拉斯矩阵的二次型，而该二次型实际上是信号在图上的平滑程度的判据［1，8］，这表明了低频特性与平滑性的等价性，也佐证了以整体RHE 作为低频假设的衡量标准是合适的.

3 拓扑约束下的最优边权重

3.1 问题描述

考虑拓扑约束下的边权重优化问题.假设已知无向无权连通图G＝（ν，ε），其中点集ν＝｛1，2，…，N｝，边集ε＝｛（u1，v1），（u2，v2），…，（uM，vM）｝，u1，u2，…，uM，v1，v2，…，vM∈ν.目标是为ε中的边构造权重，使信号在构造出的加权图上尽可能呈现低频特性.由于在实际应用中图上的信号往往是随着时间不断产生或变化的，因此希望构造的权重能够体现信号的统计特性.将信号表示为随机变量x∈ℝN，根据上节中的结论，最小化其针对加权图的拉普拉斯矩阵L 的二次型的期望：

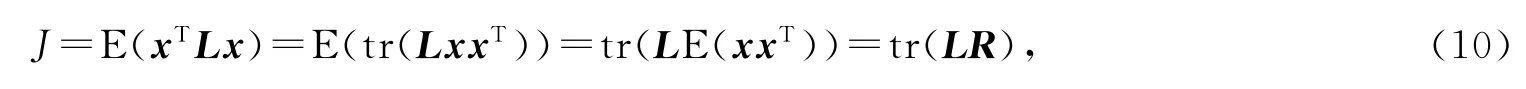
其中R＝E（xxT）为信号的二阶矩.

为了满足拓扑约束，构造的权重矩阵W 应满足如下条件

其中第一项保证权重优化过程不会导致边的增加，第二项保证权重优化过程不会导致边的减少，为预先设定的最大允许权重.注意在实际情况中，对于（i，j）∈ε，仅约束Wij＞0是不恰当的，因为若出现过小的Wij，意味着边（i，j）在信号处理过程中几乎不起作用，同样是对拓扑约束的违背.因此，有必要在目标函数中增加惩罚项，以避免出现过小的权重值.采用对数函数构造惩罚项，将式（10）中的目标函数改写为

式（12）中右边的项对较小Wij的施加较大的惩罚，并可通过参数μ 调节惩罚的力度.结合式（12）、式（11）和式（1），以及W 的对称约束，对边权重的构造可以描述为最优化问题：

3.2 问题求解

首先对式（13）中的问题进行形式简化，将优化变量W 向量化.定义关联矩阵B∈ℝN×M，其每一列对应ε中的一条边.具体地，

以pk表示边（uk，vk）的权重，即pk＝，并令p＝（p1，p2，…，pM）T，则易验证［16］

向量p 包含了矩阵W 中所有可优化的元素.将式（15）代入式（12），得到

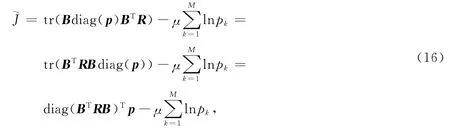
其中diag（BTRB）为包含矩阵BTRB 对角线元素的列向量.进一步，式（13）中的最优化问题可等价地描述为

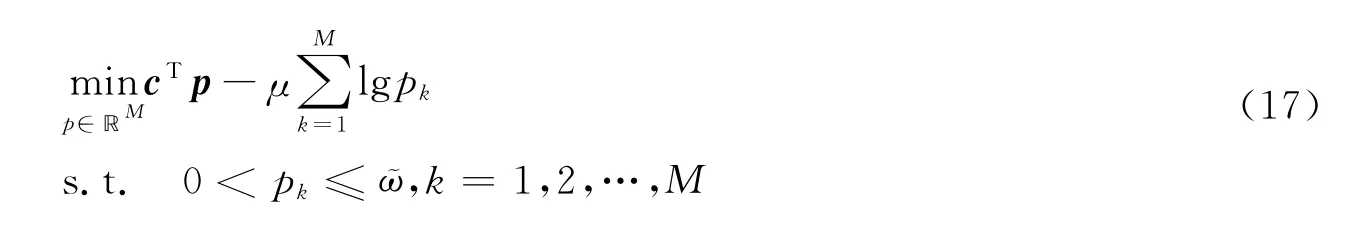
其中

定义bk＝（B1k，B2k，…，BNk）T，k＝1，2，…，M，则B＝（b1，b2，…，bM）.根据式（18），有

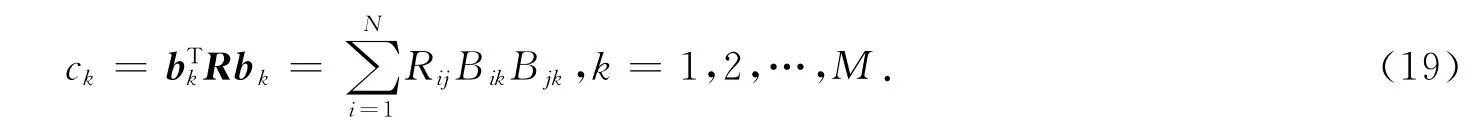
将式（14）代入式（19），得到

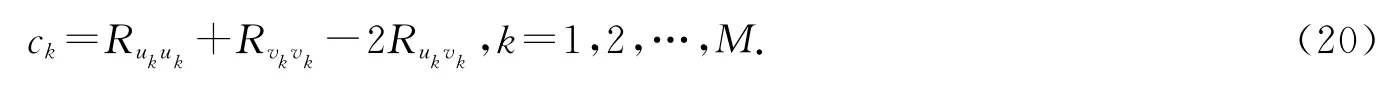
引理1 若x∈ℝN为随机变量，R＝E［xxT］，则有

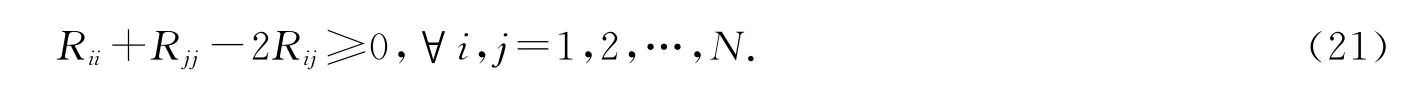
证 以Pr（X）表示随机变量（组）X 的（联合）概率密度函数，则有

注意（xi－xj）2≥0，Pr（xi，xj）≥0，∀xi，xj，因此有式（21）.

引理1证明了向量c中的元素是非负的，定理2给出了在该前提下最优权重的解析式.

定理2 假设式（21）成立，则式（17）中的问题的最优解为

证 记式（17）中目标函数为J～，其对pk的偏导数为

根据式（21）和式（20）可知ck≥0.由式（24），易知针对pk严格单调递减，在区间针对pk严格单调递增.因此当时，式（17）的最优解为时（包括ck＝0的情况），式（17）的最优解为

4 网络中的分布式权重优化算法

4.1 DOW 算法

在网络化数据处理中，图的拓扑通常来源于网络的拓扑.网络中的节点即为图中的节点，当且仅当两个节点相邻，即二者可以直接进行通信时，它们之间存在边连接.对于相邻节点i和j，根据式（23）和式（20），其间的最优边权重为

4.2 参数设置

参数T 为估计信号的二阶统计特性所用的样本数，其值越大，对信号的统计特性估计越准确，但算法需要执行的时间和通信及计算开销也越大.在实际应用中，DOW 算法得到的最优权重往往是后续信号处理算法的基础，过小的T 会影响估计的精度，进而影响后续算法的性能，而过大的T 会耽搁后续算法的执行.一般来说，T 的选择应当综合考虑应用的具体要求和信号的先验统计特性，若已知信号有较大的方差，则应当适当增加T 的值以得到较准确的估计，反之亦然.另外，当信号的统计特性发生较大变化时，应当重新执行DOW 算法以更新权重.

表1 DOW 算法Tab.1 DOW algorithm

5 仿真对比

其中（αi，βi）和（αj，βj）分别是节点i和j 的物理位置坐标，θ＞0为经验参数.当θ较大时，Wij≈1，∀i，j∈ε，此时构造的加权图接近于无权图.

每次仿真中，N 个节点均匀随机分布于单位方形区域内，两个节点相邻当且仅当两者之间的距离不大于最大通信距离d.节点在任意时刻t的数据数据x（t）∈ℝN服从均值为0、协方差为R 的高斯分布，其中

图2演示了一组通过上述方式生成的网络和数据，其中底部平面内的点和线分别代表网络中的节点和邻接关系，三维空间内的曲面高度代表各节点的数据值.

图3给出了当N＝10，d＝0.5时的一次仿真结果，其中高斯核函数法得到的图的边权重由式（28）确定，DOW 算法得到的图的边权重根据t＝1，2，…，20时的20组数据生成，图中横坐标为归一化的图的频谱，纵坐标为该20组数据在生成的图上的平均RHE 的归一化值.从图中可以看到，当高斯核函数法的θ参数值非常小时，得到的整体RHE（图中的曲线下面积）比DOW算法更小，但此时得到的图有多个接近于0的频率值，说明图被割裂为多个彼此几乎不连通的子图，这是由于过小的θ会导致出现非常小的边权重，从而破坏图的拓扑，这在实际情况中是应当避免的.当θ较大时，得到的结果与无权图非常接近，整体RHE较大，信号的低频特性不明显.而DOW 算法既得到较小的整体RHE，又避免了过小的边权重对图的拓扑的破坏.

图4为当N＝100，d＝0.2时的仿真结果，图中曲线为100次独立仿真的均值.由于每次仿真中生成的图的频谱不同，因此横坐标为频谱中频率值的编号.结果显示DOW 算法生成的图上的RHE 显著低于无权图和高斯核函数法得到的图，能够把信号能量更多地集中在低频区域.

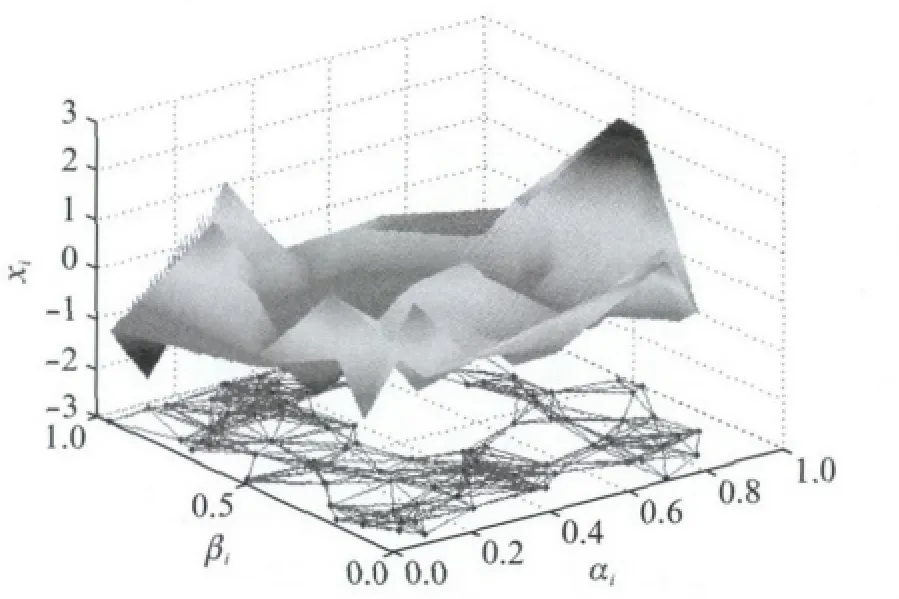
图2 包含100个节点的随机网络和高斯随机数据示例Fig.2 Example of a random network with 100nodes and Gaussian random data

图3 在一组包含10个节点的网络中得到的RHE曲线Fig.3 RHE from a network of 10nodes

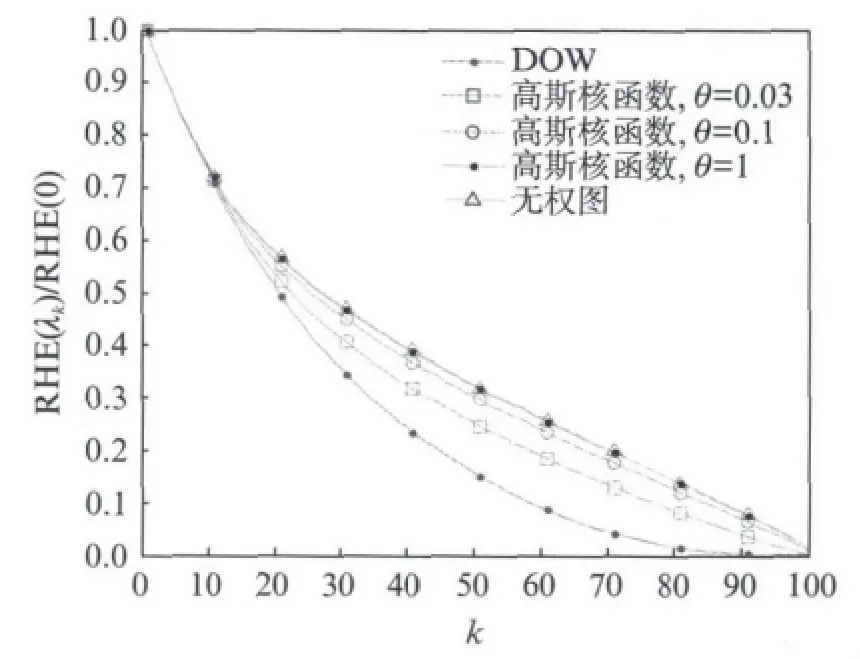
图4 在包含100个节点的网络中的平均RHEFig.4 Average RHE from networks of 100nodes

以上的仿真中均使用同样的数据样本作为DOW 算法的输入数据和计算RHE 时的输入数据.接下来用少量数据样本作为DOW 算法的输入，而用20组另外独立生成的数据来计算RHE，以测试DOW 算法得到的最优权重的泛化能力.图5给出了当DOW 算法的输入数据量T 分别为2，5和10时的仿真结果，图中显示DOW 算法得到的权重在面对新的数据时，仍能较好地反映其统计特性，将信号的能量集中在低频区域，且只需要少量数据即可达到较好效果.

接下来模拟无线传感器网络的观测方式，使用接近现实物理场的2维热扩散模型生成数据，根据该模型，位置（α，β）处在t时刻的值为

图5 通过少量训练数据得到的平均RHEFig.5 Average RHE from a small number of training data

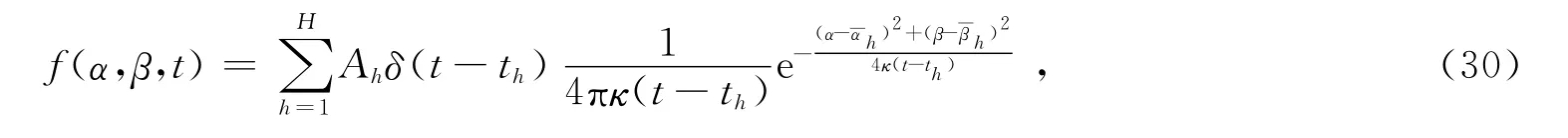
其中参数H 为热核的数目，Ah为第h 个热核的强度，th为其起始时间，为其中心位置的坐标，δ（·）为单位阶跃函数，κ为扩散因子.仿真中设置H＝50，κ＝10－4，在网络所在的单位方形区域内按均匀分布独立随机选取，th在区间［－2，－1］内按均匀分布独立随机选取，Ah在区间［－1，1］内按均匀分布独立随机选取.图6给出了一组以此参数生成的场在不同时刻的图形.在该模型下，节点i在t 时刻的数据数据即为f（αi，βi，t）.以前T 个时刻的数据为DOW 算法的输入，以t＝1，2，…，20时刻的数据计算RHE，仿真结果如图7所示，结果表明DOW 算法性能明显好于无权图和高斯核函数法.当T＝10时，DOW 算法将信号89.5%的能量集中在前20%的频率分量中，将98.5%的能量集中在前50%的频率分量中.

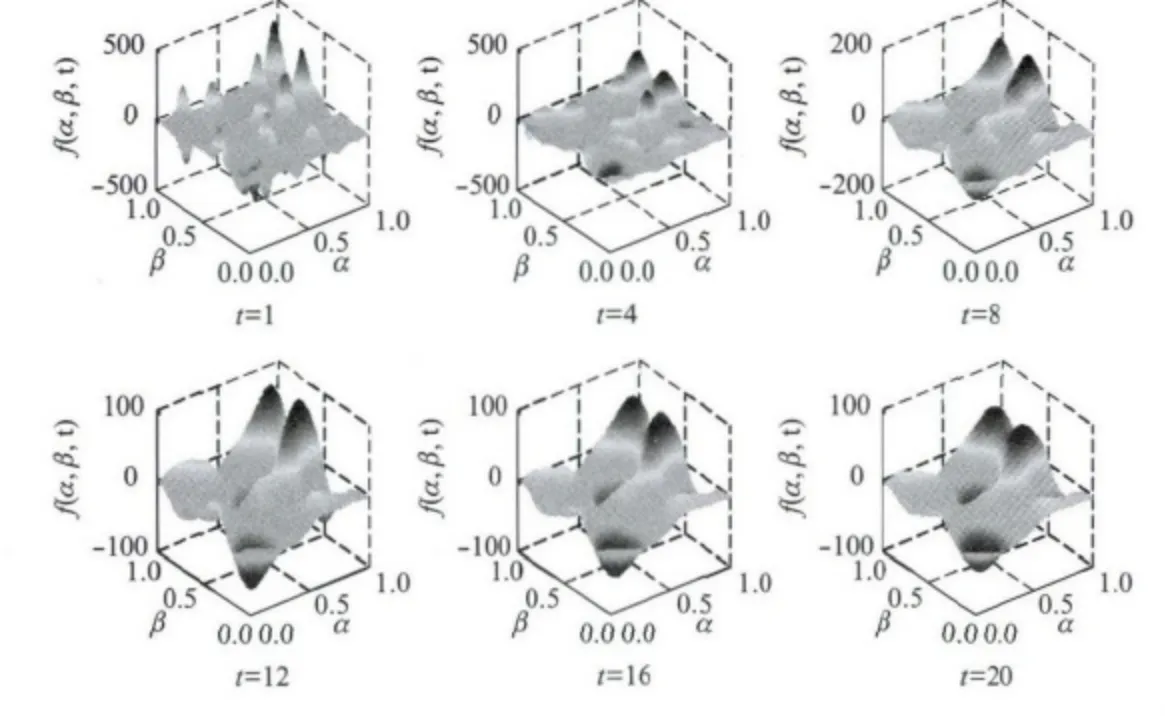
图6 2维热扩散模型得到的场Fig.6 Example of a random heat diffusion field

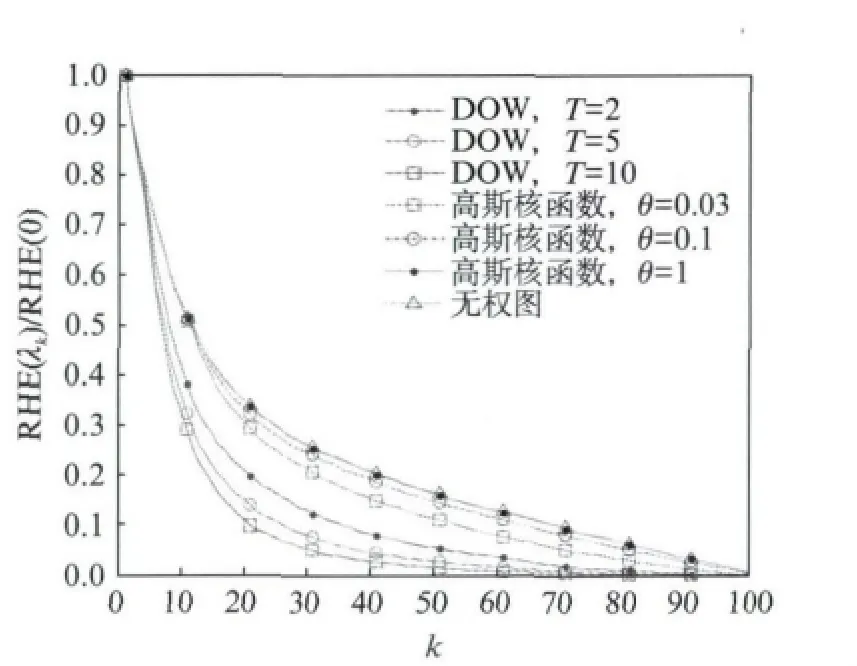
图7 以2维热扩散模型数据得到的平均RHEFig.7 Average RHE from random heat diffusion fields

6 结论

本文首先对图上的信号的低频特性进行了数学定义和分析，然后针对网络化数据处理的应用需求，提出了一种最优的边权重设计方法，使得数据在构造出来的图上的频谱可以集中在低频区段.另外，本文还提出了能够在网络中分布式计算最优权重的算法DOW，该算法基于节点的测量数据，反映了数据之间的统计特性.

本文提出的图中的边权重优化算法针对的是一般性的图上信号处理应用，而如何针对具体的图上信号处理问题设计与之匹配的边权重优化算法，使二者共同发挥最大的效益，是接下来值得研究的课题.

［1］SHUMAN D I，NARANG S K，FROSSARD P，et al.The emerging field of signal processing on graphs：Extending high－dimensional data analysis to networks and other irregular domains［J］.IEEE Signal Processing Magazine，2013，30（3）：83－98.

［2］SANDRYHAILA A，MOURA J M F.Discrete signal processing on graphs：Frequency analysis［J］.IEEE Transactions on Signal Processing，2014，62（12）：3042－3054.

［3］SANDRYHAILA A，MOURA J M F.Discrete signal processing on graphs［J］.IEEE Transactions on Signal Processing，2013，61（7）：1644－1656.

［4］ANIS A，GADDE A，ORTEGA A.Towards a sampling theorem for signals on arbitrary graphs［C］∥2014 IEEE International Conference on Acoustics，Speech and Signal Processing（ICASSP）.Florence，Italy：IEEE Press，2014：3864－3868.

［5］SHI X，FENG H，ZHAI M，et al.Infinite impulse response graph filters in wireless sensor networks［J］.IEEE Signal Processing Letters，2015，22（8）：1113－1117.

［6］SHUMAN D I，VANDERGHEYNST P，FROSSARD P.Chebyshev polynomial approximation for distributed signal processing［C］∥2011International Conference on Distributed Computing in Sensor Systems and Workshops（DCOSS）.Barcelona，Spain：IEEE Press，2011：1－8.

［7］EGILMEZ H E，ORTEGA A.Spectral anomaly detection using graph－based filtering for wireless sensor networks［C］∥2014 IEEE International Conference on Acoustics，Speech and Signal Processing（ICASSP）.Florence，Italy：IEEE Press，2014：1085－1089.

［8］DONG X，THANOU D，FROSSARD P，et al.Learning graphs from signal observations under smoothness prior［J］.arXiv preprint arXiv：1406.7842，2014.

［9］LIU D，FLIERL M.Motion－adaptive transforms based on the laplacian of vertex－weighted graphs［C］∥2014Data Compression Conference（DCC）.Snowbird，UT，USA：IEEE Press，2014：53－62.

［10］JALILI M.A graph weighting method for reducing consensus time in random geographical networks［C］∥2010IEEE 24th International Conference on Advanced Information Networking and Applications Workshops（WAINA）.Perth，WA，Australia：IEEE Press，2010：317－322.

［11］JAKOVETIC D A，XAVIER J，MOURA J M F.Weight optimization for consensus algorithms with correlated switching topology［J］.IEEE Transactions on Signal Processing，2010，58（7）：3788－3801.

［12］JALILI M，RAD A A，HASLER M.Enhancing synchronizability of weighted dynamical networks using betweenness centrality［J］.Phys Rev E Stat Nonlin Soft Matter Phys，2008，78（1Pt 2）：16105.

［13］SARDELLITTI S，BARBAROSSA S，SWAMI A.Optimal topology control and power allocation for minimum energy consumption in consensus networks［J］.IEEE Transactions on Signal Processing，2012，60（1）：383－399.

［14］SHAFI S Y，ARCAK M，EL GHAOUI L.Graph weight allocation to meet laplacian spectral constraints［J］.IEEE Transactions on Automatic Control，2012，57（7）：1872－1877.

［15］NARANG S K，GADDE A，ORTEGA A.Signal processing techniques for interpolation in graph structured data［C］∥2013IEEE International Conference on Acoustics，Speech and Signal Processing（ICASSP）.Vancouver，BC，Canada：IEEE Press，2013：5445－5449.

［16］GODSIL C D，ROYLE G.Algebraic graph theory［M］.New York：Springer，2001.