超声空化及絮体破碎过程的模拟与试验分析

郭 璇，杨艳玲，李 星，周志伟，马长红，张 洋 （北京工业大学，北京市水质科学与水环境恢复工程重点实验室，北京 100124）

超声空化及絮体破碎过程的模拟与试验分析

郭 璇，杨艳玲*，李 星，周志伟，马长红，张 洋 （北京工业大学，北京市水质科学与水环境恢复工程重点实验室，北京 100124）

为探究利于空化效应的超声条件及超声波破碎絮体机理，基于Matlab平台建立空化气泡模型及2种简化的有限扩散聚集（DLA）絮体破碎模型，进行计算机仿真，并通过试验分析得到实际絮体破碎模式.结果表明:随着超声频率的增加，空化效应减弱；声能密度的增加导致空化气泡振幅增大，声能密度为7W/mL时气泡振幅可达初始半径的200倍，空化效果较好.低声能密（0.03～3W/mL）和低超声频率（25～40kHz）处理絮体时，剥蚀作用为主导作用，超声后絮体粒径减小，分形维数增大；声能密度超过3W/mL或频率大于40kHz，大规模破碎占主导作用，实际絮体粒径减幅小且结构散.40kHz的超声频率更利于絮体的破碎，作用10min后，絮体粒径减幅达9.8%，分形维数为1.394，结构更加密实.

超声；空化效应；数值模拟；有限扩散聚集；絮体破碎

超声技术是近几年兴起的一种新型技术，在水处理及污泥预处理领域得到了广泛应用［1-3］.超声作用的主要机理为空化效应，即液体中的细微气泡被超声波激活、震荡、生长、收缩、破裂的过程［4］.空化效应是一个复杂的物理过程，空化气泡的运动受超声时间、声能密度、频率等多种因素影响［5］，对试验研究造成一定困难.本文根据热力学和运动学理论，对超声场作用下单个空化气泡的运动进行研究，分析得到超声场中气泡运动模型，考察不同频率、声能密度对空化效应的影响，从理论上探讨更利于超声作用的条件.的有效措施之一［6］，但空化效应会破坏絮体结构，改变絮体特性［7］.破碎前后絮体形态学的研究对理解超声破碎机理有重要意义，而在实际操作中很难监测破碎模式及絮体微观结构，可以借助仿真模拟来实现理论与试验的结合.近年来，一些学者借助扩散限制（DLA）模型完成了絮体生长的计算机仿真［8-9］，贺维鹏等［10］研究了破碎再絮凝的DLA絮体模型，但目前还没有关于对于超声破碎絮体的模型的报道.絮体破碎过程中存在两种破碎模式，分别为表面剥蚀和大规模破碎，前者使絮体表面的小颗粒剥落，导致小絮体颗粒浓度及尺寸范围增加，后者使絮体破碎成大小类似的碎片，而不引起小颗粒浓度变化［11-12］.本文基于以上2种絮体破碎模式，提出相应的简化超声破碎模型，在Matlab平台编写二维DLA模型，研究破碎前后DLA虚拟絮体的分形特征及超声破碎机理，同时通过超声基础试验进行分析验证.

1 试验材料与方法

1.1 超声空化气泡运动过程仿真

采用Rayleigh方程［13］的推导方法，并作出以下假设:超声场强度恒定，液体不可压缩且温度恒定，空化泡中的气体为理想气体，气泡壁只做径向运动，气泡运动过程中始终为球形且球心固定，忽略重力，考虑液体黏度和表面张力对气泡运动的影响.由质量守恒、动量守恒公式推导出多参数作用下气泡壁的运动方程:

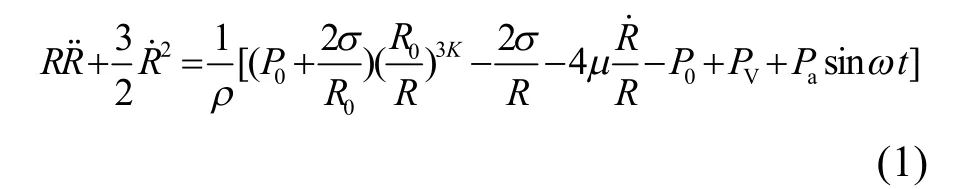
式中:R为空化泡的瞬时半径，m；R0为初始半径，m；R.为空化泡壁上质点的运动速率，m/s；R..为空化泡壁上质点的运动加速度，m2/s；ρ为液体密度，kg/m3；P0为标准大气压，Pa；Pv为空化泡内的蒸气压，Pa；Pa为超声波声压幅值，Pa；σ为液体的表面张力，N/m；k为绝热指数；μ为液体的黏度，Pa·s；ω为超声波角频率，rad/s.

通过matlab使用数值迭代法求解方程（1）并进行空化气泡运动过程的模拟.

1.2 二维DLA絮体破碎仿真

1.2.1 破碎模型建立 二维DLA絮体模型的建立与算法见文献［14］.絮体破碎过程可以看作是絮体强度与外界作用力相互竞争的结果.絮体强度的大小取决于絮体颗粒间的键的数量和强度.剥蚀作用中，絮体表面的颗粒在表面切应力作用下脱落，而絮体内部颗粒间的键不受影响［12］，基于以上思想，本文采用文献［10］的方法并加以改进，以圆心为种粒子、半径为Rb1（60、75和90）的圆截已知絮体，以模仿表面剥蚀作用.

大规模破碎作用中，施加在整个絮体中的拉应力起作用，破碎过程中絮体内部颗粒间的键被破坏，絮体整体被撕裂［12］，基于以上思想，在原絮体以外的界面随机生成的n个点，作为圆心，以圆心到生长中心距离Rb2为半径画圆截已知絮体，以此模仿大规模破碎作用.

1.2.2 参数计算 空隙率S计算公式如下［14］:

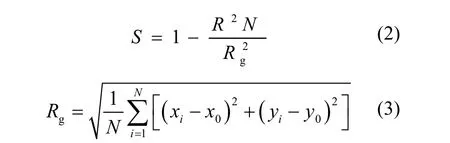
式中:N为凝聚体的粒子数；R为粒子半径；Rg为絮体最大回转半径； xi，yi为第i个粒子的坐标；x0，y0为虚拟质心坐标.

为保证模拟絮体与实际絮体参数一致性，采用图像法计算絮体二维分形维数.各条件下进行10次模拟，得10个模拟絮体，通过图像分析软件分析絮体的面积及最大长度，根据絮体投影面积与最大长度的函数关系来计算二维分形维数Df［15］:

式中:A为单个絮体的投影面积；L为单个絮体最大长度；Df为所有絮体的二维分形维数.

1.3 试验材料与方法

试验污泥为北京市某净水厂沉淀污泥，主要特性指标为温度:28.4℃，pH值:7.60，固体浓度（TS）:3.61g/L，悬浮固体浓度（SS）:2.73g/L，污泥絮体平均粒径:29.241μm，比表面积:80.282m2/g，密度:991kg/m3.

超声装置为槽式超声波反应器与探头式超声波反应器.取沉淀污泥15L至槽式装置的反应槽中（250mm×250mm×300mm），输入功率为450W，因其反应槽体积较大，有效声能密度较小，为0.03W/ml，但是超声频率可调范围较宽，因此采用槽式超声装置考察超声频率的影响.考察频率选择为25、40、125和160kHz，这几个频率较有代表性且均可通过超声装置实现.取样时间为超声10min后.

探头式超声装置的频率为25kHz，钛合金探头直径18mm，电功率0～1500W可调，本试验采用100、500和700W，对应的声能密度为1、5和7W/mL.取100mL泥样于250mL容量瓶中，将超声探头垂直伸入污泥液面10mm下，保持每次位置一致，作用过程中不控温.取样时间为超声10min后.

探头式超声装置的频率为25kHz，钛合金探头直径18mm，电功率0～1500W可调，因其反应容器较小，声能密度较大，但是超声频率可调范围有限，因此使用探头超声装置考察声能密度的影响.本试验采用30、100、300、500和700W的功率，对应的声能密度为0.03、1、3、5和7W/mL.试验中取100mL泥样于250mL容量瓶中，将超声探头垂直伸入污泥液面10mm下，保持每次位置一致，作用过程中不控温.取样时间为超声10min后.

1.4 实际絮体形态特征分析

通过光学显微镜（Olympus，BX51TF，日本）观察所截取絮体的图像，通过CCD摄像系统对絮体进行拍照，并用imageJ图像处理软件对所截取的絮体的图像、特征长度和投影面积进行分析，按式（4）计算实际絮体二维分形维数.

单个絮体粒径可用与投影面积A相等的圆直径d平均值来表征，即:

计算所截取所有絮体的当量圆直径d的均值，即为絮体平均粒径.

2 结果与讨论

2.1 空化效应模拟试验结果

空化效应受介质性质的影响，介质中的颗粒物可能减弱空化效应［4］，但由于净水沉淀污泥固体浓度较低，且密度、饱和蒸汽压等条件与水接近，各参数选择如下:R0=5μm，k=1.33，ρ=1000kg/m3，σ=0.072N/m，μ=0.001Pa·s，P0=101.3kPa，Pv=3.271Pa，初始条件t=0，R=R0，R.=0.为保证模拟试验与超声破碎污泥试验参数的一致性，选取25、40、125和160kHz为考察频率.图1反映了声能密度为0.03W/mL时，不同频率超声波作用下的模拟空化泡半径变化情况，纵坐标R（t）/R0为空化气泡瞬时半径与初始半径的比值，横坐标t/T为超声作用周期.图1中曲线在第1个周期均内有2个波峰，为稳态空化.第2个周期内，不同声频作用的空化气泡振幅有所增加，且均为瞬态空化.声频为25kHz时，空化气泡迅速膨胀，气泡达到共振，振幅可达初始气泡的45倍；超声频率继续增加，空化气泡增幅减小，125和160kHz的超声波作用下，空化气泡最大幅值仅为初始气泡的5倍左右.这是由于一方面，超声频率增大，膨胀相和压缩相时间缩短，气泡在膨胀相来不及生长成可以溃灭的空化泡，或者在压缩相来不及溃灭，导致空化效应难以进行；另一方面，频率大的超声波空化阈值较大，达到同样超声效果需要的声压较大；因此，低频率超声波更利于超声.其他试验条件相同时，应尽量采用低频超声波，以达到较好的空化效果.

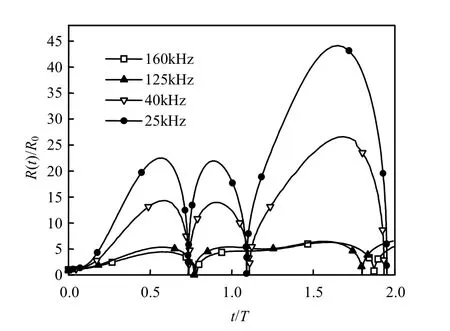
图1 不同超声频率下气泡半径随时间的变化Fig.1 Changes of cavitation bubbles radius with different ultrasound frequency

图2为其他条件不变，超声频率25kHz，声能密度为0.03、1、3、5和7W/mL的超声波作用下空化气泡变化情况.图2中除曲线1外均为瞬态空化，声能密度越大，气泡生长和溃灭越为激烈，7W/mL时空化气泡振幅可达初始半径的200倍.随着声能密度的增加，介质中超声波能量增加，负压区拉伸作用加强，空化泡生长迅速；正压区的挤压作用加剧，空化气泡迅速溃灭，气泡运动剧烈.声能密度大的超声波更有利于空化效应.

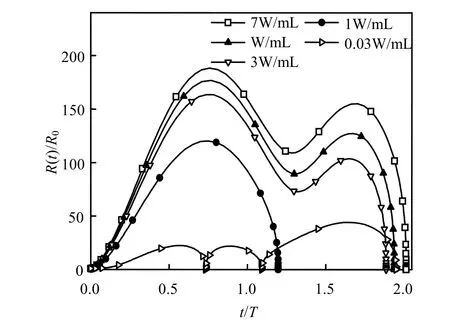
图2 不同声能密度下气泡半径随时间的变化Fig.2 Changes of cavitation bubbles radius with different energy density

2.2 DLA虚拟絮体破碎模拟试验结果

2.2.1 剥蚀作用模拟结果 超声空化气泡破裂时产生冲击波冲击固体表面，发生侵蚀、剥落作用，使絮体颗粒变小［16］.由2.1节超声空化效应的仿真结果可知，声能密度大、频率低的超声波易发生空化效应，利于破解污泥.现以破碎半径Rb的大小表示超声波破碎虚拟絮体的程度，进行剥蚀作用破碎絮体的计算机仿真.

图3反映了总凝聚颗粒数为10000、Rb为90、75、60时，破碎前后的虚拟絮体形态.由图3可知，破碎后絮体的骨架未被破坏，有明显的几何中心；絮体不规则枝杈减少，形状更加规则，粒度减小.破碎后絮体的分形维数Df随破碎半径Rb1的增加而增大，空隙率减小，回转半径内颗粒填充度增加，絮体结构变紧密.Rb1=60时，空隙率S降至0.476，减幅达45.4%；Df由1.327增至1.488，增幅仅为8.5%，小于空隙率增加速率.空隙率的大幅度减小未引起絮体结构和致密性的改善，说明靠近虚拟絮体中心的颗粒对Df的影响更大，不规则分支则对空隙率的影响更大.贺维鹏［10］研究发现破碎后虚拟絮体的不规则分枝明显减小，粒度变小的同时分形维数增加，且絮体质心附近颗粒的空间分布对虚体结构的影响更加重要，与本文结论相同.

试验研究了不同总凝聚颗粒数（5000～10000）的虚拟絮体剥蚀作用破碎前后的形态特征变化，发现分形维数与空隙率的变化规律基本相似.

2.2.2 大规模破碎作用模拟结果 超声空化气泡破裂产生的强力流体剪切力，对絮体结构产生巨大破坏，絮体被击散，尺寸减小［16］.图4为仿真得到的总凝聚颗粒为10000时，大规模破碎作用后的絮体.破碎后模拟絮体的粒径减小，不规则枝杈减少，结构较原絮体更加松散；絮体各向同性特征基本消失，表现为各向异性.总凝聚颗粒数5000～15000的虚拟絮体二维分形维数随破碎次数n（1～4）的变化如图5所示.经一次大规模破碎后，絮体破碎成两个部分，最大长度几乎不变，而投影面积减幅大，絮体更加不规则，导致分形维数由1.287～1.392减小至1.172～1.202.随着破碎次数的增加，絮体分形维数继续减小，但曲线渐趋平缓，一次破碎对絮体结构的破坏影响较大.

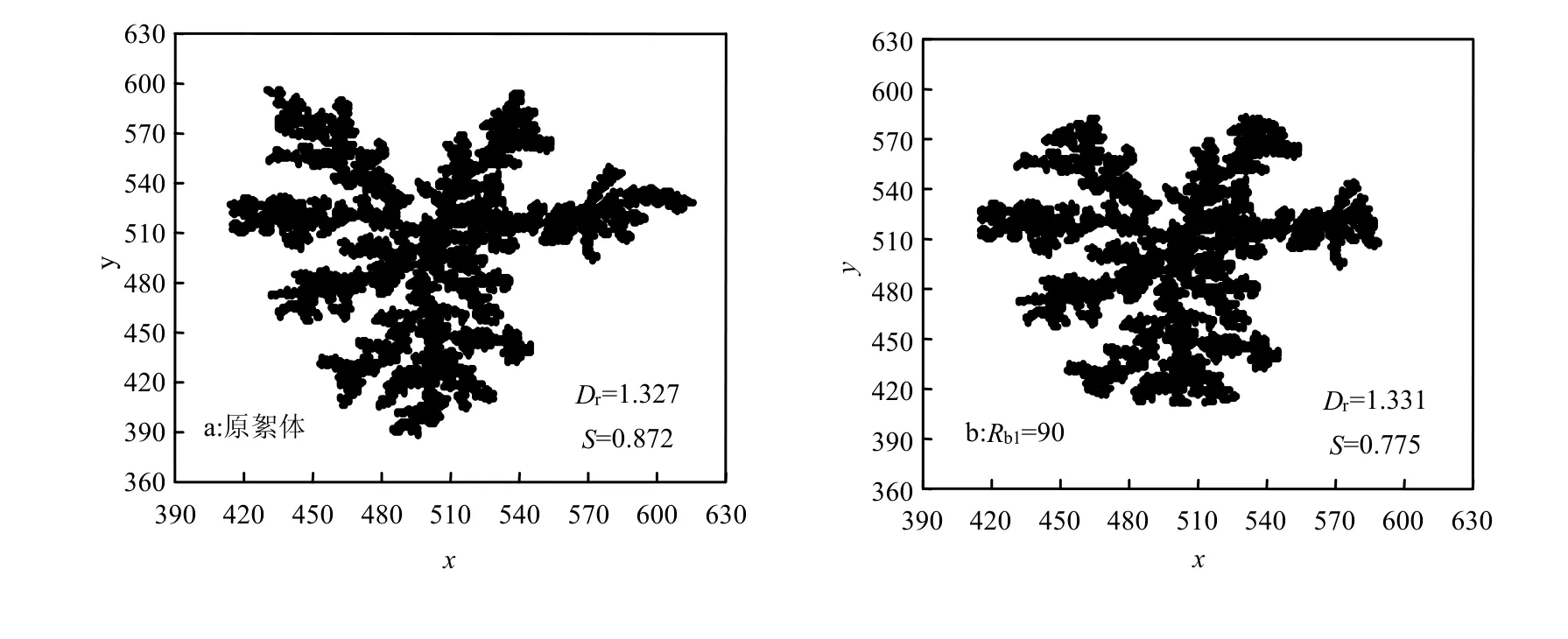
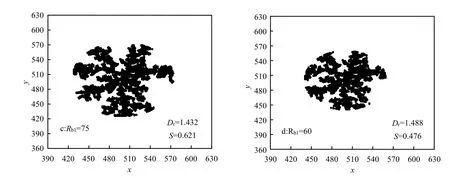
图3 不同Rb1剥蚀破碎前后的虚拟絮体Fig.3 Virtual floc before and after surface erosion breakage with different Rb1

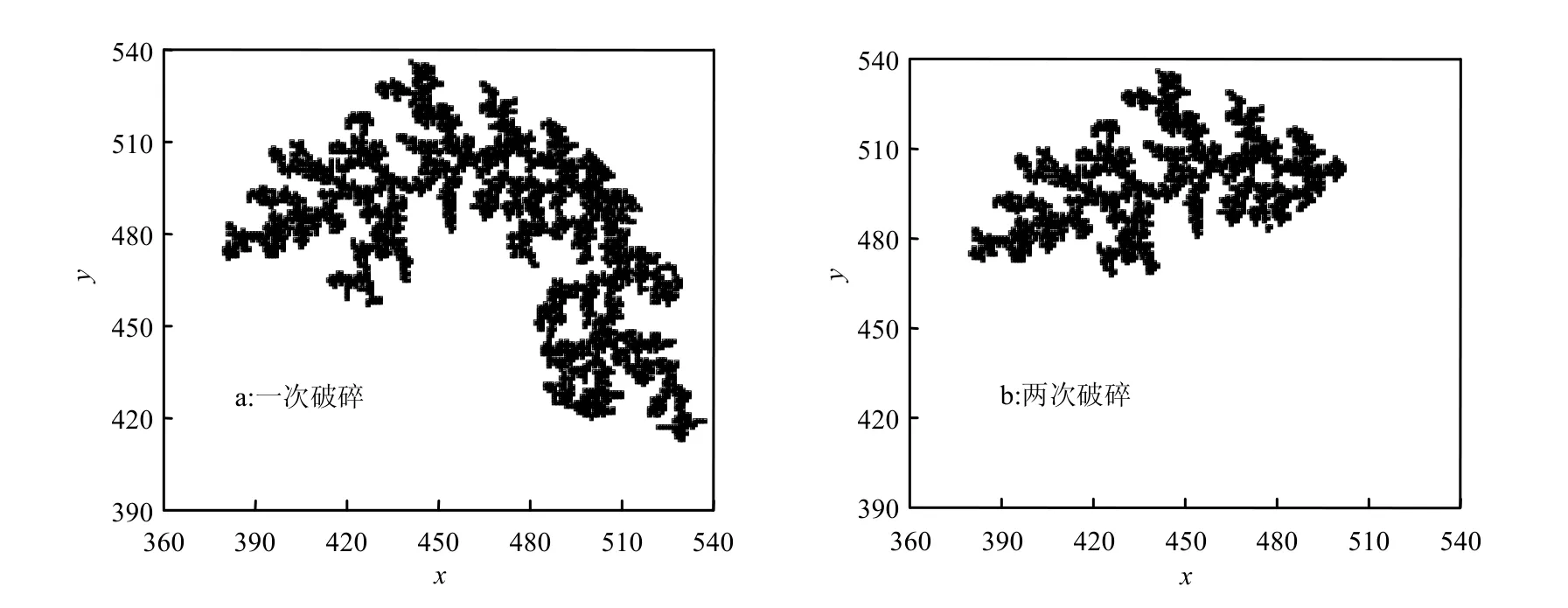
图4 大规模破碎前后的虚拟絮体Fig.4 Virtual flocs after Large Scale Fragmentation breakage

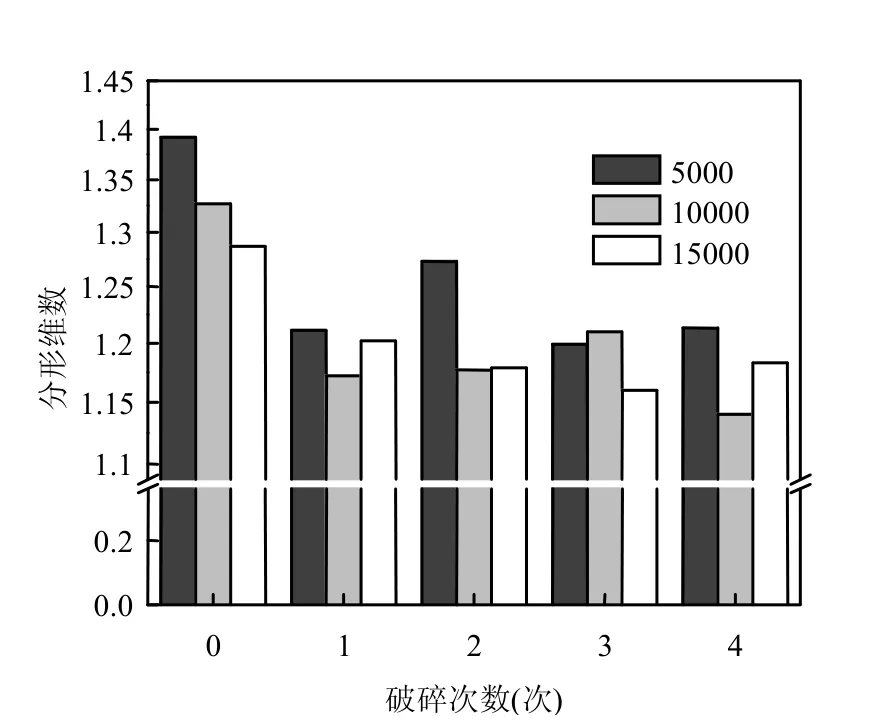
图5 大规模破碎前后的虚拟絮体分形维数Fig.5 Fractal dimension of virtual flocs after Large Scale Fragmentation breakage

2.3 超声波破解污泥絮体试验结果

采用探头式超声装置考察实际絮体经不同声能密度（0.03、1、3、5和7W/mL）的超声波作用后，絮体粒度与结构的变化结果如图6所示.随着声能密度的增加，絮体平均粒径不断减小，分形维数则是先增大后减小.超声过程中，两种破碎模式共同起作用.声能密度为0.03～3W/mL时，占主导作用的是剥蚀作用，空化气泡破裂冲击絮体颗粒表面，絮体表面的小颗粒脱离絮体，絮体粒径减小，分形维数增大，絮体结构更加密实.声能密度增加到3W/mL以上，絮体破碎更加明显，结构被破坏，分形维数降低.此时大规模破碎为主导作用，空化气泡破裂产生的强水喷射流，形成巨大水力剪切力［17］，絮体被打碎，污泥中小颗粒数目整体增加，且絮体结构变得松散，不利于沉降.声能密度越高，絮体破碎越明显，超声空化效应容易发生，与2.1节超声空化气泡运动模拟结果相符.

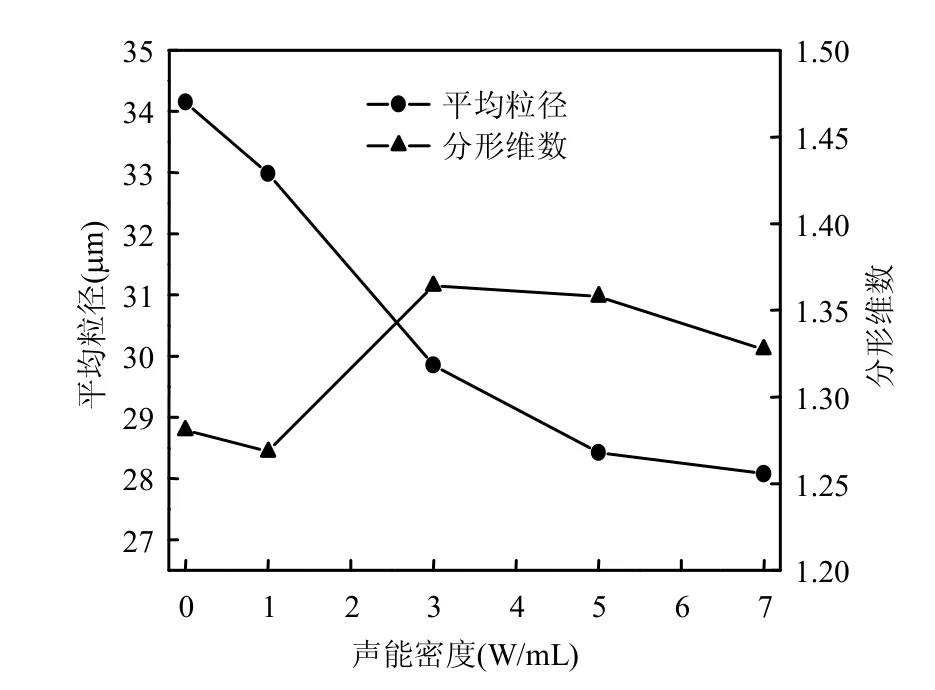
图6 声能密度对絮体粒度及结构的影响Fig.6 Effects of energy density on flocs size and structure

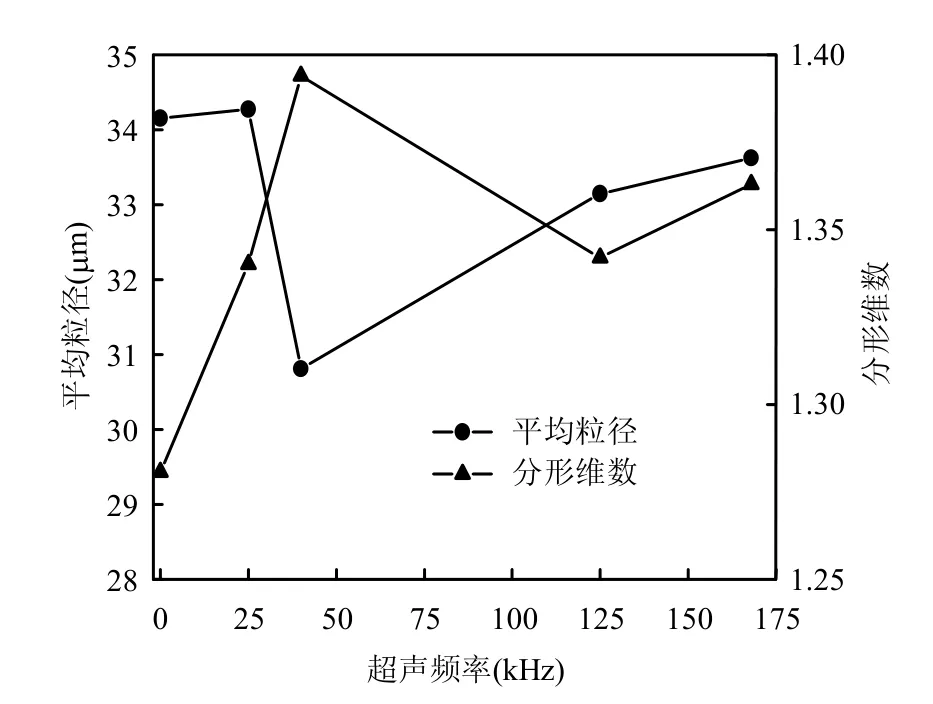
图7 超声频率对絮体粒度及结构的影响Fig.7 Effects of ultrasound frequency on flocs size and structure

图7为超声频率对实际絮体粒度及结构的影响.由图7可知，40kHz的超声频率更利于超声破解污泥，且超声后的污泥絮体分形维数最大，絮体内填充程度高，更加规则.超声频率继续增大，絮体粒径增加，这可能是因为一方面空化效应随超声频率增加减弱，不利于絮体破碎，絮体粒径减小缓慢；另一方面，超声波海绵效应促使水从絮体内部沿波面传播时产生的通道通过，使污泥颗粒凝聚，尺寸增大，增加到一定程度后相互碰撞凝结［18］，絮体粒径增加.由分形维数的变化趋势可以推测，超声频率小于40kHz时，剥蚀破碎为主导作用，经超声破碎后絮体变得密实、规则；大于40kHz时，空化效应减弱，大规模破碎作用增强，与海绵效应共同作用，导致絮体粒径减幅小且结构松散，破解效果较差.空化气泡模拟结果显示频率小的超声波更利于空化效应的发生，实际结果则显示40kHz为最佳破碎频率，可能的原因是超声波在污泥介质传播时伴随着能量的衰减、扩散，污泥吸收的超声能量小于输入值；另外超声破碎污泥是空化效应、海绵效应、机械效应等共同作用的结果，40kHz的超声波可能更利于机械效应等的发生.

3 结论

3.1 超声空化气泡运动过程仿真结果表明:超声频率与声能密度均对空化效果产生影响.超声频率越大，形成的空化气泡振幅较小，空化效应减弱.声能密度较大时，介质中的空化气泡运动剧烈，空化效应增强.

3.2 DLA虚拟絮体破碎模拟试验结果表明:剥蚀作用后，虚拟絮体粒径减小，分形维数增大，孔隙率减小；絮体形状更加规则，内部填充程度增大.大规模破碎作用后，虚拟絮体粒径与分形维数均降低，絮体变得小而松散.

3.3 超声破碎实际絮体实验结果表明:声能密度较低时，剥蚀作用为主导作用，超声后实际絮体粒径减小，分形维数增大，结构更加密实；声能密度超过3W/mL，大规模破碎占主导作用.超声频率较低时，剥蚀作用为主导作用.40kHz的超声频率处理实际絮体后，絮体粒径减幅大、结构密实.频率大于40kHz，剥蚀作用减弱，大规模破碎作用增强，实际絮体粒径减幅小且结构松散.

［1］Pilli S， Bhunia P， Yan S， et al. Ultrasonic pretreatment of sludge: A review ［J］. Ultrasonics Sonochemistry， 2011，18（1）:1-18.

［2］宫常修，蒋建国，杨世辉.超声波耦合Fenton氧化对污泥破解效果的研究 ［J］. 中国环境科学， 2013，33（2）:293-297.

［3］胡健龙，冉治霖，李绍峰，等.超声灭活饮用水中隐孢子虫研究［J］. 中国环境科学， 2014，34（2）:431-436.

［4］Show K Y， Mao T H， Lee D J. Optimisation of sludge disruptionby sonication ［J］. Water Research， 2007，41:4741-4747.

［5］张 红，丁述理，徐博会，等.超声空化气泡运动的数值模拟 ［J］.河北工程大学学报（自然科学版）， 2013，30（4）:103-107.

［6］邬 艳，杨艳玲，李 星，等.超声作用对净水沉淀污泥絮体特性的影响 ［J］. 中国环境科学， 2014，34（5）:259-265.

［7］Laurent J， Casellas M， Dagot C. Heavy metals uptake by sonicated activated sludge: Relation with floc surface properties［J］. Journal of Hazardous Materials， 2009，162（4）:652-660.

［8］Witten T A ， Sander L M. Diffusion-limited aggregation:a kinetic critical phenomenon ［J］. Physical Review Letters， 1981，47（19）: 1400-1403.

［9］Deng L， Wang Y S， Ou-yang Z C. Diffusion-limited aggregation with polygon particles ［J］. Communications in Theoretical Physics， 2012，58（6）:895-901.

［10］贺维鹏，南 军，施 周，等.絮体破碎过程的仿真及试验分析［J］. 中国环境科学， 2013，33（10）:1779-1784.

［11］Mikkelsen L H， Keiding K. The shear sensitivity of activated sludge: An evaluation of the possibility for a standardised floc strength test ［J］. Water Research， 2002，36（12）:2931-2940.

［12］Jarvis P， Jefferson B， Gregory J， et al. A review of floc strength and breakage ［J］. Water Research， 2005，39（14）:3121-3137.

［13］Rayleigh J W. On the Pressure developed in a liquid during the collapase of a spherical cavity ［J］. Philosophical Magazine，1917，34（200）:94-98.

［14］蒋文天，邱祖民.絮凝体DLA模型仿真及其废水处理 ［J］. 计算机与应用化学， 2009，26（2）:233-239.

［15］Chakraborti R T， Atkinmin J F， Van B， et al. Characterization of alum floc by image analysis ［J］. Environmental Science and Technology， 2000，34（18）:3969-3976.

［16］宋新南，刘莉红，侯李平，等.超声破解对污泥表面性质的影响［J］. 江苏农业科学， 2012，40（1）:329-331.

［17］薛玉伟，季 民，李文斌.超声功率对超声破解污泥的影响 ［J］.化工学报， 2007，58（4）:1038-1041.

［18］张光明，常爱敏，张盼月.超声波水处理技术 ［M］. 北京:中国建筑工业出版社， 2006:146-147.

Simulation of ultrasound cavitation bubble and numerical/experimental analysis of flocs breakage process.

GUO Xuan，YANG Yan-ling*， LI Xing， ZHOU Zhi-wei， MA Chang-hong， ZHANG Yang （College of Architecture and Civil Engineering，Beijing University of Technology， Beijing 100124， China）. China Environmental Science， 2015，35（5）：1429～1435

In order to explore the sonication condition for the ideal cavitation effect and to find out the breakage mechanism of flocs exposed to ultrasound， a model of cavitational bubble and two sorts of simplified models of diffusion-limited aggregation （DLA） floc breakage were established and simulated based on Matlab. The practical flocs breakage patterns were verified through experimental analysis. The results indicated that the cavitation effect decreased as the ultrasonic frequency increased. The increase of ultrasonic density led to the increscent amplitude of cavitation bubble，when the sonication density was 7W/mL， the radius of cavitation bubbles can be enlarged to 200 times longer and the cavitation effect was fairly good. When the flocs were treated at low energy density （0.03～3W/mL） and low frequency（25～40kHz） ultrasonication， surface erosion dominated the breakage effect， which was reflected by decreased radius and increased fractal dimension of flocs. When the energy density exceeds 3W/mL or the frequency surpasses 40kHz， the large scale fragmentation was the main mechanism， leading to the smaller flocs size and looser structures. The sonication of the frequency of 40kHz is more beneficial to flocs breakage， with the experimental result that 10minutes' ultrasonication can lead to a dinimutioin rate of 9.8% of the radius and a fractal dimension of 1.394， and the structure of the flocs were more compact.

ultrasound；cavitation effect；numerical simulation；diffusion-limited aggregation；flocs breakage

X703，TU991.2

A

1000-6923（2015）05-1429-07

郭 璇（1991-），女，北京人，北京工业大学建筑工程学院硕士研究生，主要从事饮用水安全研究.

2014-09-30

国家自然科学基金项目（51278005）；北京市自然科学基金项目（8132007）；国家水体污染控制与治理科技重大专项（2012ZX07404-003）

* 责任作者， 研究员， yangyanling@bjut.edu.cn