金属熔体中超声声空化特性的研究进展

王旭东，黄海军，周月明

（1.宝山钢铁股份有限公司，上海 201900；2.上海交通大学，上海 200240）

超声处理是实现金属凝固细化的高效方法，大量的研究发现在液态金属及其凝固过程中引入超声能显著细化凝固组织[1～3]，而且该方法不仅较化学法具有不“污染”熔体的优点，还兼有工艺简单，普适性强、成本低廉的特点。这使得通过施加超声以控制金属熔体的凝固过程，实现晶粒细化的工艺更具吸引力和广阔的前景。

超声对金属凝固组织的影响主要是通过超声过程中产生声空化。声空化是指波在液体中传播时引发液体“撕裂”致使空穴或气/汽穴即空化泡的产生、膨胀与溃灭的一系列过程。伴随声空化的发生，在周围液体中产生奇特的声空化效应：释放压力激波,产生微射流。在金属熔体中，一方面压力激波引起平衡熔点升高造成过冷，从而促进均值或抑制形核；另一方面，在压力激波与微射流共同作用下，金属熔体浸入其中杂质表面的狭缝或凹槽中，从而“活化”杂质而形核；再者，熔体在凝固过程中，压力激波或微射流“折断”枝晶，造成晶粒增殖。通过这些方式，在金属熔体或其凝固过程中施加超声处理使得凝固组织得以细化。

1 空化泡的形成

一般认为当负压达到或超过空化阈值，液体被撕裂并形成空化泡。然而负压及撕裂过程极大地影响局部物理条件，这势必造成气体脱溶与液体蒸发，形成含气空化泡——空化气泡，或含汽空化泡——空化汽泡，或气与汽兼有的混合空化泡，而这些过程之间的相互作用并不十分清楚。

Kwak等[4]研究了过饱和液体中气泡的形成，认为负压首先造成气体脱溶形成气泡团簇（cluster[5]）。团簇的形成过程可由气体分子的碰撞模型表示为：

则该团簇的形核率为：

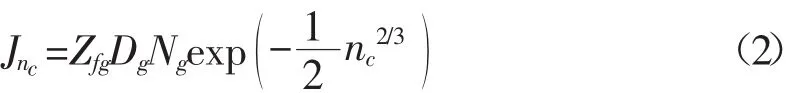
式中，n为气泡中的分子数目；βg为适应系数（acommodation coeffcient）：V¯为熔体中的平均分子流速；N¯g为单位体积熔体中溶解的平均气体分子数；Zfg为Zeldovich非平衡系数。类似于液-固相变形核，气泡团簇通过气体分子的扩散或合并，长大形成临界气泡核。然而，S Stralen[6]认为相对于汽化形核而言，通过气体脱溶成核很有限，并从理论上给出了推导。Pratap S.Bapat[7]把水考虑成简单立方结构，汽化（vaporization）造成分子沿相邻7个方向迁移形成分子空穴（void），进而通过空穴间的合并形成空化气/汽核。进而从热力学上分析了空化泡的形成，认为空化泡形核能接收的声能量并不能独立支撑形核，需要核周围液体的温度起伏以及分子间“碰撞”产生的能量（Free energy of collision among molecules）辅助，并给出了形核率：

其中，σ为界面张力；m为气/汽体分子质量；ρg与ρ1分别为气/汽体与液体密度；ΔGv为对应的形核功。同时Pratap S.Bapat[7]还考虑了脱溶（desorption）造成的空化气核，然而这两类形核相互独立，气体的脱溶与溶液的汽化隔离。

实际的液相中不可避免存在表面粗糙的金属氧化物、难溶非金属夹杂等，这使得空化泡以此为核心异质形核，研究[4]表明位于难溶夹杂物表面的凹槽能有效形核，即便槽内气体浓度低于平衡浓度。张华伟[8]从理论上给出了气泡在凹槽内的形核能力，相比均质形核，气泡在凹槽内异质形核形核能减小f（θ,α）倍：

式中，α、θ分别为凹槽近似锥顶角与面接触角。

2 声空化结构与声空化泡分布

声空化泡的分布是衡量超声空化行为的重要指标[9]。一方面，在微观上声空化泡在声场中自组织形成空化结构[10]。在第一Bjerknes力（primary Bjerknes force）作用下，声空化泡在声空间运动形成动态纤维状（filamentary）主干[11]；同时由于第二Bjerknes力（secondary Bjerknes force）的作用，空化泡在局部聚集产生声空化泡簇。典型结构如图1所示[14]，这种单纤维状的空化结构能长时间“稳定”动态存在，空化泡之间存在动态的合并，及单个空化泡溃灭产生子空化泡。对于这种“稳定”结构当前并没有很深刻的认识，可能的原因是由于在空间位置稳定存在空化泡的异质核心以及在其周围空化泡的均质形核[12,13]。对于不同的声场条件，空化结构表现出不同的特征[13]。

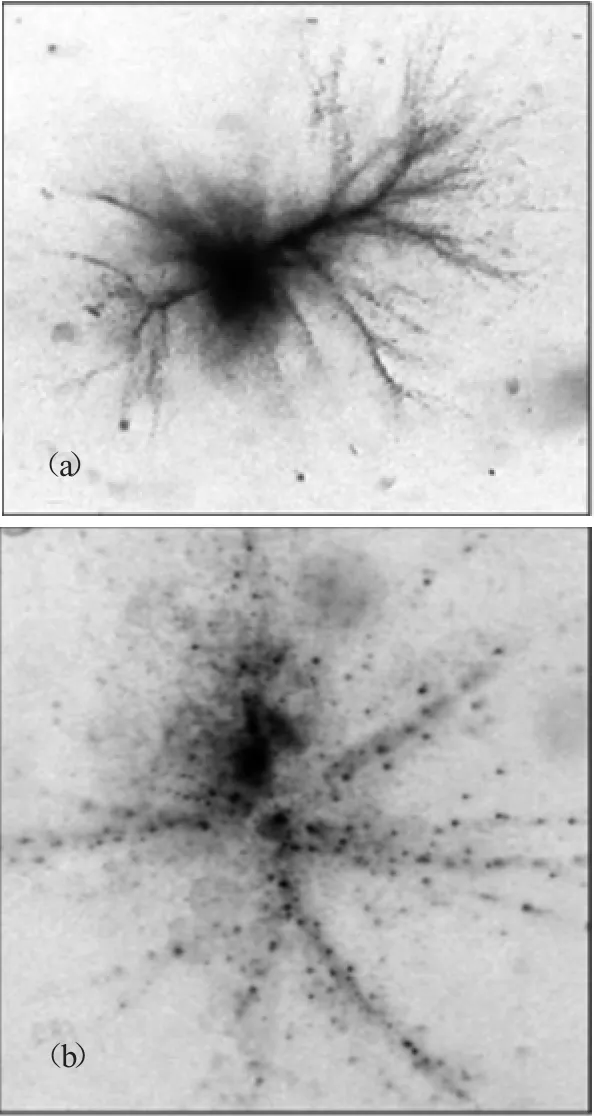
图1 不同曝光时间条件下水中的声空化结构（a）20ms （b）5μs

另一方面，就宏观分布（位置、尺寸）而言，当前对于离散空化泡分布的研究主要分为两类，一类是直接观测的方法，如采用高速摄影的方法[15]，发现声空化泡集中于声发射端面近邻，并随着远离程度的增加，声空化泡的数目逐渐减少。然而这种方法较为定性[16]，为深入了解声空化泡的分布，另一类采用间接检测手段，通过检测声空化泡的分布对物理量的影响，然后反推出声空化泡的分布。J.Frohly[17]利用电磁共振频率变化而获得空穴溶解速率变化（void rate dissipation）的方法定量的给出了水中声空化泡的尺寸分布，表明随着驱动声压的增大及声辐射时间的延长声空化泡在尺寸分布上向小尺寸段聚集。但在试验中声空化泡沿着声发射端面近似呈二维分布，并不能反映三维空间中声空化泡的分布，而且声空化泡的捕捉范围有限（19μm～51μm）。Avvaru[18]通过利用分析声散射谱的方法研究了水中空化泡的分布，发现在20kHz的频率条件下，空化泡的尺寸在50～80μm。A.Prosperetti[19]假定空化泡尺寸呈“截断”高斯分布，Rashid Jamshidi考虑高斯分布的空化泡对声传播的阻尼作用，并结合波动方程数值计算了声空化区的存在，数值结果表明声空化区近邻声发射端，并随着声输出功率的增大与输出频率的减小，声空化区增大，同时声空化区还与反应器的几何有关。G.Servant进一步考虑可压缩气泡流体，“截断”高斯分布的声空化泡在流体中连续分布，考虑声空化泡与声压间的相互作用，通过求解Caflisch方程更精确预测了声空化区，求解出声空化泡的体积随时间的变化；并考虑两相流，通过求解Euler方程求解空化泡在梯度声压力，粘滞力及浮力作用下，声空化泡体积随时间的分布。然而，此类数值方法只能将空化泡作为整体——空化云，用于处理并不能在长程空间跟踪各分离的空化泡。

3 空化泡动力学

对于空化泡的动力学，大多聚焦于单个空化泡[20,21]。早在1917年，Rayleigh[22]为研究空化泡溃灭，提出了不可压缩流体中球形空化（气）泡绝热运动方程：

后来Plesset考虑了表面张力和液体粘度等的影响进行了修正，形成了经典的Rayleigh-Plesset（R-P）方程并广泛用来描述声压驱动下空化泡的运动，即[22]：

式中，R为空化泡半径；d R/d t泡壁移动速率，当取正时表示膨胀，反之表示收缩；pin为泡内压力，μ为液体粘度。

对于可压缩流体，Gilmore提出了著名的Gilmore 方程[23]：

式中：

Gilmore方程中考虑了声空化泡对入射超声波的耗散，Keller与Miksis更完备的考虑了声辐射衰减，提出了K-M方程[24]：

不同于Gilmore方程，K-M方程中的衰减前置因子中取声速c为常数，而且熵H仅取一阶[25]。

然而，上述方程假设空化泡内所含气体的含量不变，在其径向振动过程中始终保持球形，内部压力场保持均匀。然而当驱动声压达到一定值时，空化泡内气体与周围液体产生整流扩散（Rectified diffusion）[26]，即在周期性声压作用下，空化泡内气体含量增加，此时R-P方程并不能准确描述空化泡的长大过程。对于整流扩散，泡内压力pin=pg，pg为气体压力pin=pg，pg其满足气体状态方程：

而气体密度pg与温度Tg分别由质量守恒和能量守恒方程控制，即[27]：

液体温度Tl满足：

液体中溶质浓度满足：

式中：

当空化泡紧邻壁面时，在其径向振动过程中并非保持球形，受壁面约束。在刚性壁面附近，空化泡溃灭时球形失稳；在轴对称弹性壁面条件下，空化泡呈椭球状径向振动[28]。实际上空化泡溃灭时，“裂变”产生小的子空化泡，这势必改变原母空化泡的球形状态[29]，而对此当前并没有深刻的理论认识。

对于空化泡构成的空化云（图2）研究相对较少[30]。当前对空化云动力学的研究主要可分为两类[31]。第一类把空化云作为一整体，不考虑单个空化泡的动力学以及它们之间的相互作用。第二类则把空化云内空化泡之间的相互作用作为研究重点，然而空化云内空化泡数目十分有限。无论对于第一类或第二类，对于包含n个空化泡的空化云，其作为整体假设其在径向振动过程中中心位置不变，保持球形，并且与周围液体无质量交换等，其边界在超声场内满足另一种形式的R-P方程：

其中α为空化云半径。同时，空化云内空化泡也分别同样满足该R-P方程：

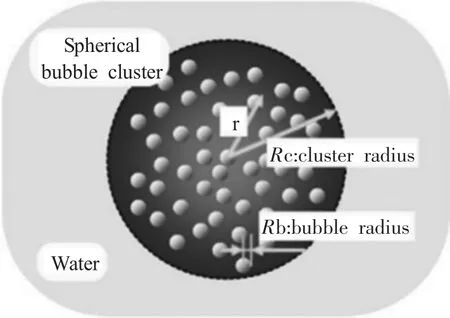
图2 空化云示意图

在空化云径向振动的过程中，空化云内液体体积保持不变：

对水中的空化云从理论与实验上研究发现[32]：空化云呈现2倍及多倍于单个空化泡周期径向振动，当增多空化云区大尺寸空化泡，其呈亚谐波径向振动；在多分散系统中，空化云中空化泡呈现同周期性，整体空化效应得到加强。空化云溃灭产生的激波不同于单个空化泡，激波向空化云中心传播，并在中心聚焦[33,34]。

4 空化泡的运动学

在声场作用下，空化泡受到Bjerkness力、粘性力及浮力等的作用，在液体中产生运动；同时空化泡的径向振动引起壁面的“扰动”，使得空化泡的运动变得复杂。因而，难以探讨与实验验证一般声场作用下空化泡的运动学问题，大多工作在驻波条件下展开。

在弱声场作用下，当声压驱动频率低于空化泡本征频率时，空化泡向波腹运动；而当声压驱动频率高于空化泡本振频率时，其向波节运动。Eller[35]从理论上研究单个空化泡在声场作用的受力，在Z轴对称柱面波时，Bjerkness力：

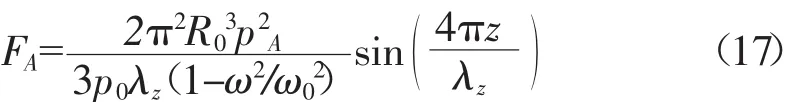
其运动方向决定于声驱动频率ω与空化泡本振频率ωo的相对大小。

在强声场作用下，空化泡存在两种运动模式：一是随意“舞蹈”运动（erratic“dancing”motion）,另一种则是在波腹与波节之间来回运动。对于空化泡的“舞蹈”运动，被认为是声压驱动下参数化的空化泡壁径向振动造成[36,37]。Alexander[38]详尽推导出了描述该“舞蹈”运动的方程组：

式中，s为空化泡的形状模式（shape mode）；g（t）与f（t）分别是关于空化泡半径R及形状模式s的函数。对于第二种运动，其与形状模式无关，而主要是由于在低本征频率的空化泡在强声压作用时Bjerknes力的方向改变引起。Mettin[39]考虑由于强声压作用下R-P方程不能准确描述空化泡的高幅径向振动，通过修正K-M方程并结合Lagrangain方程推导出了描述该运动的方程组：

式中，x表示空化泡中心的空间位置；FB为Bjerknes力。

5 结论与展望

超声细化的在关键在于超声过程中的声空化行为，涉及声空泡的形成，声空化泡的形态与分布，声空化泡的动力学与运动学等特征，从而影响超声对金属凝固组织的细化作用。然而，由于常见金属的非透明性，及合金熔体性质受合金成分与温度的影响，适应于具体金属熔体中声空化特性尚缺乏理论与实验研究，这严重制约超声对金属的细化理论发展，从而影响超声细化方法在金属领域的应用与推广。

近年来，随着第三代同步辐射X射线光源的发展，应用基于同步辐射X射线成像技术研究非透明介质，特别用以实时原位研究金属内部组织越来越普遍与深入，这为实验研究金属熔体中的声空化行为提供了新的思路与可能。在同步辐射X射线成像实验研究的基础上，建立描述不同金属熔体中声空化行为的理论模型，从而深入研究金属熔体中的声空化行为，推动超声细化理论的发展及超声细化方法的应用。

[1] QIAN M,RAMIREZ A,DAS A.Ultrasonic refinement of magnesium by cavitation：Clarifying the role of wall crystals[J].J Cryst Growth,2009,311(14)：3708-15.

[2]JIAN X,MEEK T T,HAN Q.Refinement of eutectic silicon phase of aluminum A356 alloy using high-intensity ultrasonic vibration[J].Scripta Mater,2006,54(5)：893-6.

[3]RAMIREZ A,QIAN M,DAVIS B,et al. Potency of high-intensity ultrasonic treatment for grain refinement of magnesium alloys[J].Scripta Mater,2008,59(1)：19-22.

[4] KWAK H Y,YONG W K.Homogeneous nucleation and macroscopic growth of gas bubble in organic solutions[J].International Journal of Heat&Mass Transfer,1998,41(4-5)：757-67.

[5]KWAK H Y,PANTON R L.Gas bubble formation in nonequilibrium water-gas solutions [J].J Chem Phys,1983,78(9)：5795-9.

[6] STRALEN S V,COLE R.Boiling phenomena：physicochemical and engineering fundamentals and applications[M].Hemisphere Pub.Corp,1979.

[7] BAPAT P S,PANDIT A B.Thermodynamic and kinetic considerations of nucleation and stabilization of acoustic cavitation bubbles in water[J].Ultrason Sonochem,2008,15(1)：65-77.

[8]张华伟,李言祥.金属熔体中气泡形核的理论分析 [J].物理学报,2007,56(8)：4864-71.

[9] LEIGHTON T G.Bubble population phenomena in acoustic cavitation[J].Ultrason Sonochem,1995,2(2)：S123-S36.

[10]MOUSSATOV A,METTIN R,GRANGER C,et al.Evolution of acoustic cavitation structures near larger emitting surface;proceedings of the World Congress on Ultrasonics[C],Paris(France),2003：955-958.

[11]MOUSSATOV A,GRANGER C,DUBUS B. Cone-like bubble formation in ultrasonic cavitation field [J].Ultrason Sonochem,2003,10(4-5)：191.

[12]PARLITZ U,METTIN R,LUTHER S,et al.Spatio-temporal dynamics of acoustic cavitation bubble clouds[J].Philosophical Transactions of the Royal Society A Mathematical Physical&Engineering Sciences,1999,357(1751)：313.

[13]METTIN R,LUTHER S,OHL C D,et al.Acoustic cavitation structures and simulations by a particle model [J].Ultrason Sonochem,1999,6(1-2)：25-9.

[14] LUTHER S.Theoretische Beschreibung und experimentelle Untersuchung raum-zeitlicher Strukturbildung in akustischen Kavitationsblasenfeldern [J].Elektronische Ressource ，2003：1475-1478.

[15]SHU D,SUN B,MI J,et al.A High-Speed Imaging and Modeling Study of Dendrite Fragmentation Caused by Ultrasonic Cavitation [J].Metall Mater Trans A,2012,43(10)：3755-66.

[16]IIDA Y,ASHOKKUMAR M,TUZIUTI T,et al.Bubble population phenomena in sonochemical reactor：I estimation of bubble size distribution and its number density with pulsed sonication- laser diffraction method [J].Ultrason Sonochem,2010,17(2)：473-9.

[17]LABOURET S,FROHLY J.Bubble size distribution estimation via void rate dissipation in gas saturated liquid.Application to ultrasonic cavitation bubble fields [J].Eur Phys J AP,2002,19(1)：39-54.

[18]AVVARU B,PANDIT A B.Oscillating bubble concentration and its size distribution using acoustic emission spectra[J].Ultrason Sonochem,2009,16(1)：105.

[19]COMMANDER K W,PROSPERETTI A.Linear pressure waves in bubbly liquids：Comparison between theory and experiments[J].J Acoust Soc Am,1989,85(2)：732-46.

[20]BARBER B P,PUTTERMAN S J.Light scattering measurements of the repetitive supersonic implosion of a sonoluminescing bubble[J].Phys Rev Lett,1992,69(26)：3839.

[21]GAITAN D F,CRUM L A,CHURCH C C,et al.Sonoluminescence and bubble dynamics for a single,stable,cavitation bubble[J].J Acoust Soc Am,1992,91(6)：3166-83.

[22]AND M S P,PROSPERETTI A.Bubble Dynamics and Cavitation [J].Annual Review of Fluid Mechanics,1977,9(1)：145-85.

[23]GILMORE F R.The growth or collapse of a spherical bubble in a viscous compressible liquid [J].California Institute of Technology,1952：1-40.

[24]KELLER J B,MIKSIS M.Bubble oscillations of large amplitude[J].J Acoust Soc Am,1980,68(2)：628-33.

[25]HOLZFUSS J.Acoustic energy radiated by nonlinear spherical oscillations of strongly driven bubbles [J].Proceedings Mathematical Physical&Engineering Sciences,2010,466(2118)：1829-47.

[26]ELLER A,FLYNN H G.Rectified Diffusion during Nonlinear Pulsations of Cavitation Bubbles [J].J Acoust Soc Am,1965,37(3)：493.

[27]MEIDANI A R N,HASAN M.A study of hydrogen bubble growth during ultrasonic degassing of Al-Cu alloy melts[J].J Mater Process Technol,2004,147(3)：311-20.

[28]FARONG,GAO,CAIHUA,et al.Constrained oscillation of a bubble subjected to shock wave in microvessel[J].Progress in Natural Science：Materials International(自然科学进展：国际材料(英文)),2009,19(9)：1109-17.

[29]PRESTON A T,COLONIUS T,BRENNEN C E.Toward Efficient Computation of Heat and Mass Transfer Effects in the Continuum Model for Bubbly Cavitating Flows [J].Cav Fourth International Symposium on Cavitation,2001：1-7.

[30]MATSUMOTO Y,YOSHIZAWA S.Behaviour of a bubble cluster in an ultrasound field [J].Int J Numer Methods Fluids,2005,47(6-7)：591-601.

[31]NASIBULLAEVAÉS,AKHATOV I S.Dynamics of a bubble cluster in an acoustic field [J].Acoust Phys,2005,51(6)：705-12.

[32]TERVO J T,METTIN R,LAUTERBORN W.Bubble Cluster Dynamics in Acoustic Cavitation[J].Acta Acustica United with Acustica,2006,volume 92(92)：178-80.

[33]MATSUMOTO Y,ALLEN J S,YOSHIZAWA S,et al.Medical ultrasound with microbubbles [J].Experimental Thermal&Fluid Science,2005,29(3)：255-65.

[34]SHIMADA M,MATSUMOTO Y,KOBAYASHI T.Dynamics of the Cloud Cavitation and Cavitation Erosion [J].Nihon Kikai Gakkai Ronbunshu B Hen/transactions of the Japan Society of Mechanical Engineers Part B,1999,65(634)：1934-41.

[35]ELLER A.Force on a Bubble in a Standing Acoustic Wave[J].J Acoust Soc Am,1968,43(1)：170-1.

[36]BENJAMIN T B,ELLIS A T.Self-propulsion of asymmetrically vibrating bubbles [J].J Fluid Mech,2006,212(212)：65-80.

[37] MEI C C,ZHOU X.Parametric resonance of a spherical bubble[J].J Fluid Mech,2006,229(229)：29-50.

[38]DOINIKOV A A.Translational motion of a bubble undergoing shape oscillations [J].J Fluid Mech,2004,501(501)：1-24.

[39]DOINIKOV A A.Translational motion of a spherical bubble in an acoustic standing wave of high intensity [J].Phys Fluids,2002,14(4)：1420-5.