一种基于卡尔曼和线性插值滤波的改进三角质心定位算法*

赵大龙，白凤山，董思宇，李洪书

（内蒙古大学电子信息工程学院，呼和浩特 010021）

一种基于卡尔曼和线性插值滤波的改进三角质心定位算法*

赵大龙，白凤山*，董思宇，李洪书

（内蒙古大学电子信息工程学院，呼和浩特 010021）

基于RSSI的目标定位技术，由于复杂度低、定位精度较高，被广泛用于无线传感网络节点定位中。为进一步提高无线移动定位精度，首先利用CC2530构成的参考节点的RSSI实测数值得到无线信道模型中优化射频参数A和传播因子n，通过卡尔曼滤波和线性插值法对随机误差进行补偿以获得较精确的定位节点与参考节点间的估计距离；然后采用一种改进的三角质心定位算法进行测试与仿真。通过仿真证明，采用的改进算法较传统的加权质心算法在定位精度上有较明显的提高，在所测试环境下平均定位精度为0.7米左右，获得了较好的效果。

无线移动定位；RSSI；卡尔曼滤波；线性插值；三角质心定位

随着无线传感器网络和物联网技术的蓬勃发展，基于无线传感网络的定位技术［1］被广泛应用到众多领域。无线传感器网络定位系统［2］是指自组织网络通过特定方法确定节点位置信息的系统。在无线传感器网络中，按照是否依靠测距定位分为基于测距［3］（range-based）和非基于测距［4］（range-free）的定位算法。前者是利用测量和估计得到节点间的距离，然后通过几何关系来估算节点位置，如接收信号强度（RSSI）、信号传播时间/时间差/往返时间（TOA［5］/TDOA/RTOF）、接收信号相位差（PDOA）等方法。后者是利用节点间的跳数与参考节点位置等信息估计出每一跳的距离，从而估计出节点的位置［6］。从定位精度方面分析，基于测距的定位算法可获得较高定位精度，大多数现有的定位系统均采用基于测距的定位算法。

RSSI测距是利用信号在传播中存在信号强度衰减的方法，通过信道传播模型计算距离。但是，这种计算方法容易受到各种传播因素的影响。因此，对测量数据进行数据处理、校正尤为重要。卡尔曼（Kalman）滤波算法是一种比较好的数字滤波方法，该方法不仅有效地抑制了距离数据信息的误差发散，而且能充分利用线性插值法对随机误差进行补偿。

在滤波算法中［7-9］，文献［9］利用卡尔曼滤波算法，对RSSI进行滤波，并估测出移动节点的运动轨迹，较其他处理方法可获得较高的测距精度［10-11］。但是，这种方法的缺点是在测距阶段没有充分利用信标节点的信息，使得RSSI测距值存在较大误差。

在无线移动定位算法中［12-16］，文献［12］提出一种实用的加权三角质心RSSI定位算法，即通过RSSI测距技术测量节点间的距离，并优选信标节点，最后用三角加权质心方法进行定位。该方法的优点是计算简单，定位过程中无需增加节点间额外通信开销。但是，该方法存在的缺点是在圆周定位模型中没有充分利用距离d信息，定位误差精度较低。

本文对文献［9］和文献［12］算法的漏洞进行修改，通过卡尔曼滤波和线性插值法修正RSSI值，并采用传统的距离损耗模型计算d；在基于改进的加权三角质心RSSI测距［17-18］的基础上计算未知节点坐标。通过MATLAB仿真表明，此算法进一步提高了节点定位精度，具有较好的实用价值。

1 RSSI测距与数据处理

1.1 RSSI测距

基于RSSI测距的定位方法是无线传感网络节点定位的主要方法之一，大多数无线传感网络CCx系列芯片均提供RSSI测量数据。RSSI测距算法的基本思想是指在发射节点的发射功率确定的情况下，可以根据接收节点接收的功率，得出能量损耗与距离的关系。通常采用的信号传播模型如公式（1）所示［19］。

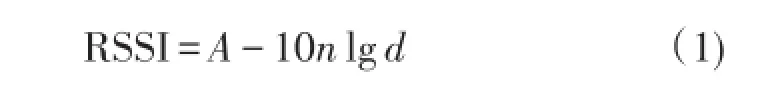
式中，RSSI为接收信号强度（dBm）；A常取距离发射结点1 m时的接收信号强度；d是收发节点之间的距离（m）；n表示信号传播常量，也叫信号传播因子。因此，定位前合理选取A和n是提高距离测量精度的前提。

本实验选择空旷的操场上测试，节点芯片为CC2530，天线为2.4 G全向天线，增益为3 dBi，天线长度为109 mm。首先将用于接收数据的定位节点1固定好，发射结点在距其1 m位置以功率为0 dBm连续发射功率信号，测量一组20个数据；为减少天线方向性产生的辐射偏差，将发射节点沿着顺时针方向再转90°，进行第二组20个数据的测试，这样旋转一周将所测得的同一距离内的80个数据信号强度求平均值，作为该距离内的接收信号实测值，测试节点分布如图1所示。

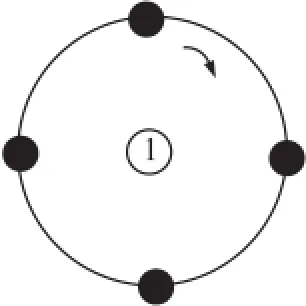
图1 测试节点分布

接着距定位节点每增加0.5 m重复上述测量过程，最后绘制成图2中的点画曲线作为RSSI实测曲线。取距离1 m时的接收信号强度的平均值-30 dBm作为参数A的取值，再通过变化n，由公式1利用MATLAB可以绘制出多条RSSI与d关系曲线，如图2所示。

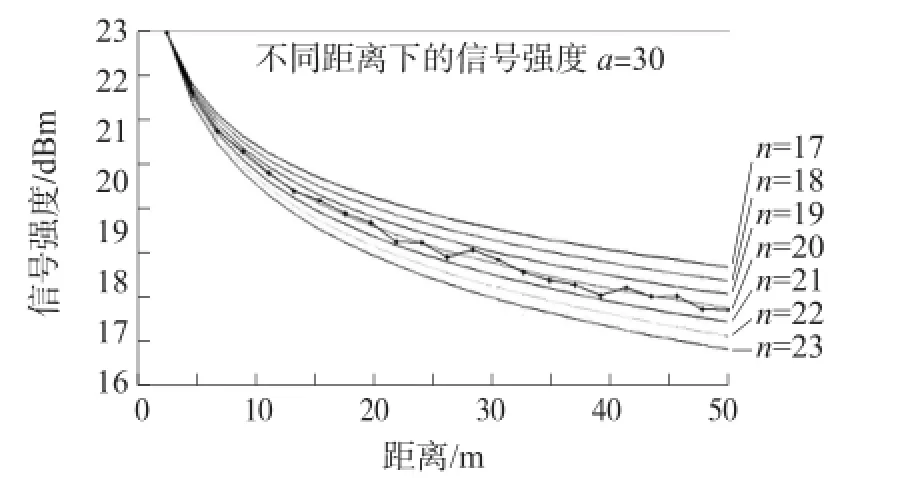
图2 RSSI与d对应关系

通过对比拟合曲线与n取不同值时的曲线的拟合度来确定n。由表1中可以看出n取20的拟合曲线的拟合度为0.99，表明RSSI均值和距离之间存在确定的函数关系，而且在20 m内，RSSI实测值与理论分析比较接近。

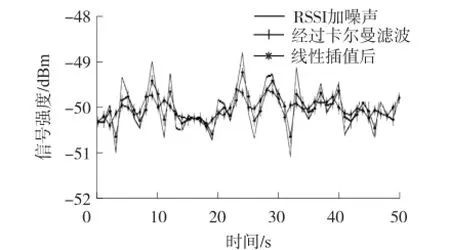
图3 RSSI数据修正前后对比

表1 拟合度对比表

有了A和n，接收节点根据接收到信号的强度RSSI就可以利用式（1）估算出与几个发射节点的距离d，从而利用定位算法计算出未知节点的位置。

1.2 卡尔曼滤波

RSSI数据容易受到各种干扰噪声的影响，为了满足对定位精度的进一步要求，还需要对上述数据进行处理。文献［19］中给出了几种不同数据滤波方法的效果对比，其中卡尔曼滤波算法表现出良好特性。

卡尔曼滤波是以最小均方误差为估计的最佳准则来寻求一套递推估计的算法。其基本思想是：采用信号与噪声的状态空间模型，利用前一时刻的估计值和现时刻的观测值来更新对状态变量的估计，求出现时刻的估计值。当对象模型足够准确且系统状态和参数不发生突变时，性能较好。该方法简单，数据存贮量小，具有很强的实时性。

本文采用卡尔曼滤波方法对各信标节点的RSSI测距数据进行处理，以达到快速收敛，减少噪声影响和误差目的，卡尔曼算法原理详见参考文献［7-10］。

1.3 线性插值

线性插值是数学、计算机图形学等领域广泛使用的一种简单插值方法。假设已知坐标（x0，y0）与（x1，y1），要得到［x0，x1］区间内某一位置xi在线上的yi值，可由线性插值法的求得：

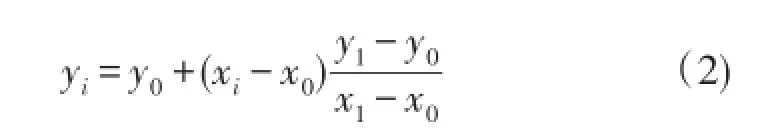
这种在一组点（x0，y0）、（x1，y1），…，（xn，yn）中插值的方式可被定义为点对之间的线性连续插入，可产生一条实线。本文中将经卡尔曼滤波处理的RSSI数据用线性插值方法来预测已知的多对点对之间的未知点的信号强度。数据处理结果对比如图3所示。从图3可以看出，处理后的RSSI可减小波动，说明卡尔曼滤波和线性插值法对提高无线定位稳定性和准确性有很大作用。

2 三角质心定位算法的改进

2.1 传统的质心定位算法

传统的质心定位算法是距离加权质心定位算法，即找出距未知节点最近的三个参考节点（未知节点接收到RSSI最强的三个节点），并按照公式（1）将计算出这三个参考节点与未知节点之间的距离作为权值引入到定位算法中，然后求这三个参考节点的质心作为未知节点的位置估计，见图4（a）。

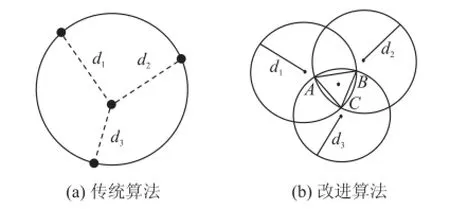
图4 基于圆周模型的三角质心算法

一般来说，已知无线传感器网络N个固定信标节点Bi的位置坐标（xi，yi），其中（1≤i≤N），未知节点的估计位置坐标为（x，y），那么传统基于RSSI的加权质心定位算法计算公式为：

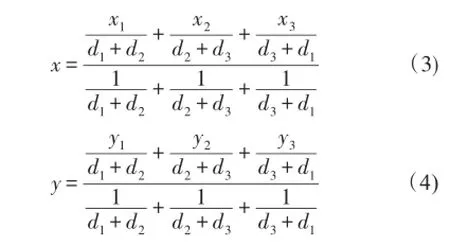
这里权值是未知节点到固定信标节点的距离函数和的倒数。传统的质心定位算法最简单，但定位精度较低，使用较少。

2.2 改进的质心定位算法

根据文献［12］提到的传统加权质心定位算法的原理可知，权值这一部分对于整个算法定位精度有着至关重要的作用，合理选取权值可以避免信息淹没现象。加权质心定位算法中对于权值选择可以采用不同的方式，本文中采用距离倒数之和代替传统算法中距离和的倒数的算法。

首先将接收到的RSSI数据利用卡尔曼滤波和线性插值修正，并利用公式（1）转化为距离。再将这些距离从小到大进行排序，选距离最小所对应的3个信标节点用于对未知节点定位。然后分别以这3个信标节点为圆心，以未知节点到信标节点之间的距离为半径画圆，由于实际测量结果每次都有误差，这样3个圆不会交于一点，而会产生公共相交部分，如图4（b）所示。此时，未知节点就认为位于所有圆的交集部分。以上述提到的质心算法为基础，对3个圆的共同交点（ABC）组成的三角形进行分析，利用优选的参考节点和未知节点之间的距离为每一个坐标增加了权值，以体现不同顶点的贡献。

修正后的加权质心公式为式（5）和式（6）。其中（xA，yA）、（xB，yB）、（xC，yC）为三个交点坐标可以容易求出，式（5）和式（6）不仅在质心运算中增加了RSSI数据的信息，还在权值的选取中合理的安排了信息权重，并采用了修正系数的概念，使得整个定位精度得到了很大的提高。

但是在实际的测试中，由于测距误差，三个圆往往无法交于一点。假设移动节点只在参考节点的区域内活动，则可能产生的情况如图5所示。

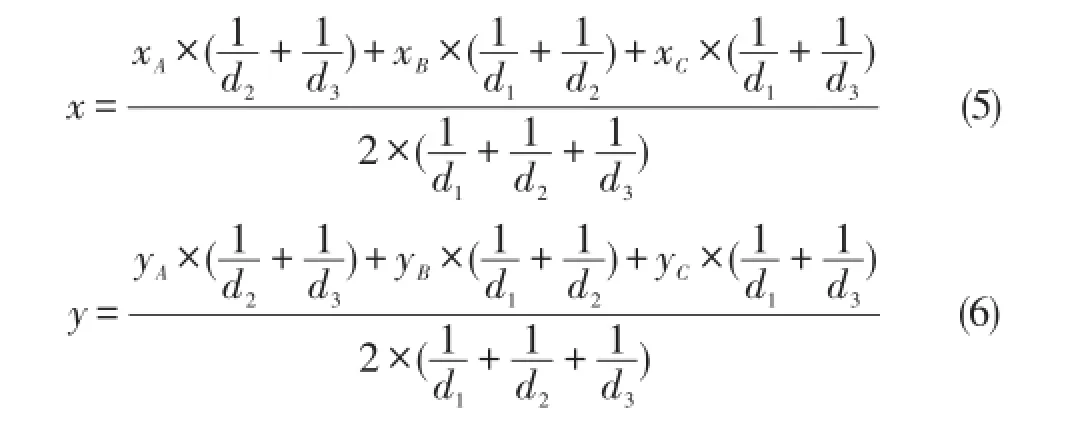
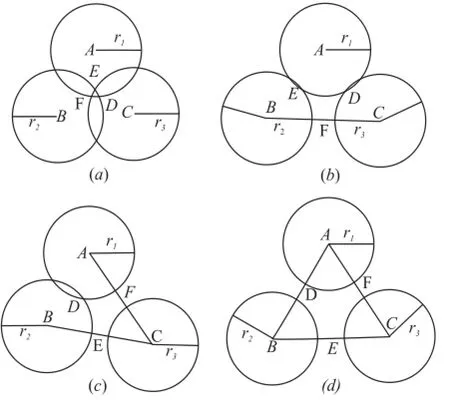
图5 三边定位测算中可能发生的四种情况

实际操作中，首先要判断3个圆之中有几个相交，采用的方法可以是把3个圆的方程两两联立，判断有没有解。

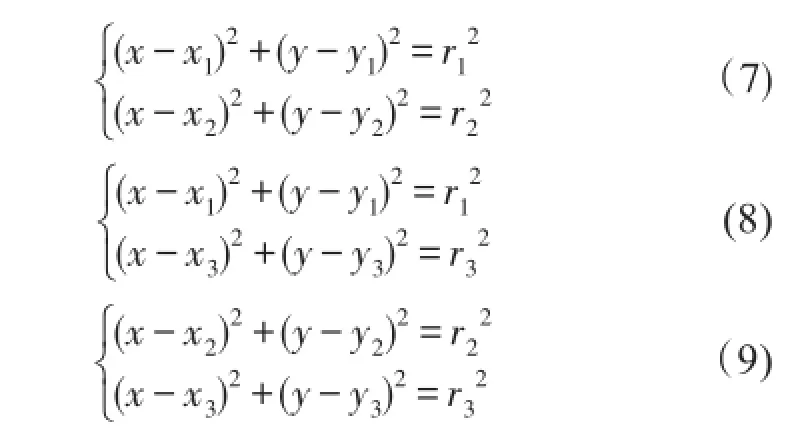
如果方程（7）有解（x12，y12）和（x21，y21），判断其中哪个点与点（x3，y3）的距离近，选取该点作为点D；如果方程（8）有解（x13，y13）和（x31，y31），判断其中哪个点与点（x2，y2）的距离近，选取该点作为点F；如果方程（9）有解（x23，y23）和（x32，y32），判断其中哪个点与点（x1，y1）的距离近，选取该点作为点E，则△DEF的重心就是我们所需要定位的移动节点的位置。如果其中方程（7）无解，则连接两圆圆心，和圆相交两点的中心就是点D；对于式（8）和式（9）无解的情况下，可采用相同方式来得到点E、F的坐标。因此，无论圆相交与否，我们都可以获得3个点D、E、F，并且通过求重心来获得移动节点的坐标。

3 算法实现与仿真

3.1 算法实现过程

改进定位算法实现流程如下：

（1）各信标节点周期性发送自身信息：节点ID、自身位置信息；

（2）未知节点收到信息后，记录信标节点ID对应的RSSI值，并利用卡尔曼滤波和线性插值法对RSSI数据进行修正；

（3）未知节点接收到一定的坐标信息后，不再接收新信息，对信标节点依其RSSI值从大到小排序，并建立RSSI值与未知节点到信标节点距离的映射，建立3个集合：

①信标节点集合：Beacon=｛a1，a2，…，am｝；

②未知节点到信标节点距离集合：Distance= ｛d1，d2，…，dm｝，d1＜d2…＜dm；

③信标节点位置集合：

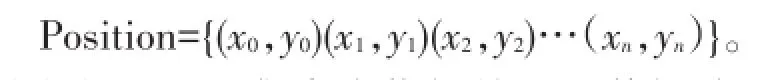
（4）在Beacon集合中依据前述对传播路径损耗模型的分析结论，优先选择RSSI值中最大的三个信标节点组合成下面的集合：

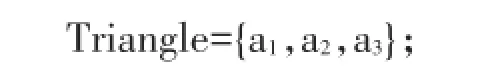
（5）将Beacon中的RSSI值转换为距离d，并从大到小排序：

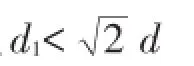
（6）分别对三组数据进行计算产生三个定位点A、B、C的坐标，如图4（b）。再用修正的加权质心算法式（5）、式（6）求得三角形质心（x，y）作为未知节点的位置坐标。

3.2 算法仿真

为了对本文采用的基于卡尔曼滤波和线性插值法的改进三角质心定位算法进行验证，我们采用MATLAB软件，利用Shadowing模型进行仿真。仿真实验的初始条件为：无线传感器网络位于30 m×30 m的区域内，4个信标节点等间距分布在正方形区域四个角上，为了验证简单性，本文把未知节点初始化为（0，15），未知节点在中线上以匀速向右移动。路径损耗系数n设为20，节点的通信半径为30 m，仿真环境如图6所示。

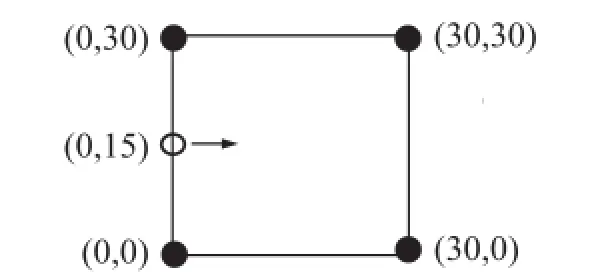
图6 仿真环境

另外，所有的仿真实验环境中都加入了均值为零，标准差为0.5的高斯分布随机噪声，来代替实际环境中的反射、多径、物体移动、气候等带来的影响。

图7给出了滤波前、单独卡尔曼滤波、滤波与线性插值结合三种情况下改进三角质心定位算法的有效性。在周围信标节点总数为4时，该算法平均定位误差在0.7 m左右。由此可见，相对于传统的基于RSSI的质心定位算法，首先通过卡尔曼滤波和线性插值法对随机误差进行补偿以；然后采用改进的三角质心定位算法定位，有着明显优势，大大的提高了算法的定位精度。

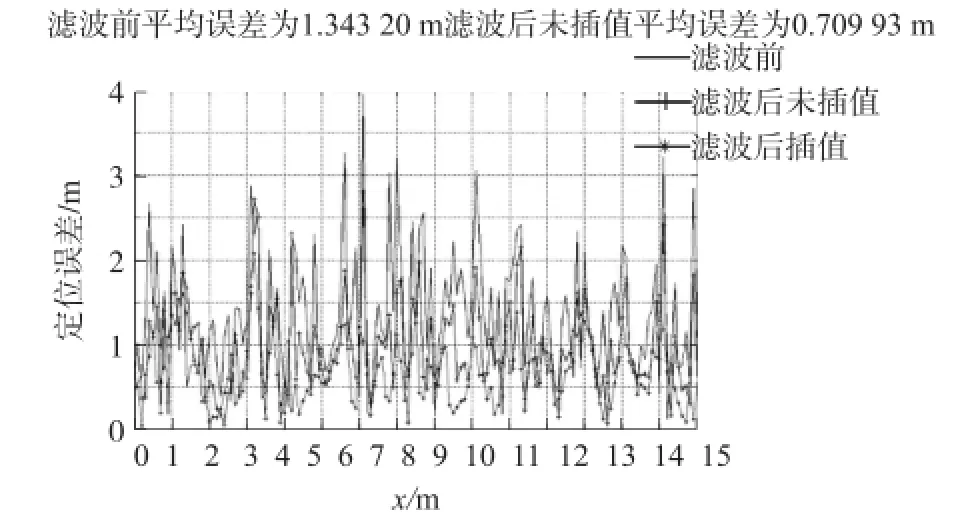
图7 三种条件下定位算法测距误差仿真

4 结论

本文采用通过卡尔曼滤波和线性插值对节点发射的RSSI修正，然后运用改进的三角质心定位方法计算未知节点位置。实验和仿真表明该定位算法不仅具有更好的定位精度，而且算法运算量较小，对硬件的要求不高，比较适合对节点定位精度要求不太高的大规模传感器网络应用中，经过进一步改进后将具有较高的实用价值。

［1］ 周雅琴，谭定忠.无线传感器网络应用及研究现状［J］.传感器世界，2009（5）：35-40.

［2］ Liu Yunhao，Yang Zheng，Wang Xiaoping.Location，Localization and Localizability［J］.Journal of Computer Science and Technology，2010，25：274-297.

［3］ 吴晓平，陆炳斌，沈浩.基于RSSI定位模型的非视距关系识别方法［J］.传感技术学报，2013，26（11）：1584-1589.

［4］ Zhang Shigeng，Cao Jiannong，Chen Lijun，et al.Accurate and Energy-Efficient Range-Free Localization for Mobile Sensor Networks［J］.IEEE Transactions on Mobile Computing，2010，9（6）：897-910.

［5］ Junyang Shen，Andreas F Molisch，Jussi Salmi.Accurate Passive Location Estimation Using TOA Measurements［J］.IEEE Transactions on Wireless Communications，2012，11（6）：2182-2192.

［6］ Yang Zheng，Liu Yunhao.Understanding Node Localizability of Wireless Ad Hoc and Sensor Networks［J］.IEEE Transactions on Parallel and Distributed Systems，2012，11：1249-1260.

［7］ 刘志华，马征征，陈嘉兴.无线传感器网络中移动节点的后验信号滤波定位法［J］.传感技术学报，2013，26（5）：739-744.

［8］ 朱明强，侯建军，刘颖，等.一种基于卡尔曼数据平滑的分段曲线拟合室内定位算法［J］.北京交通大学学报，2012，36（5）：95-99.

［9］ 邓胡滨，张磊，吴颖，等.基于卡尔曼滤波算法的轨迹估计研究［J］.传感器与微系统，2012，31（5）：4-7.

［10］Paul A S，Wan E A.RSSI-Based Indoor Localization and Tracking Using Sigma-Point Kalman Smoothers［J］.IEEE J of Selected Topics in Signal Processing，2009，3（5）：860-873.

［11］曹春萍，罗玲莉.基于卡尔曼滤波算法的室内无线定位系统［J］.计算机系统应用，2011，20（11）：76-79.

［12］杨博雄，倪玉华，刘琨，等.基于加权三角质心RSSI算法的Zig-Bee室内无线定位技术研究［J］.传感器世界，2012，11：31-35.

［13］Wang Gang，Yang Kehu.A New Approach to Sensor Node Localization Using RSS Measurements in Wireless Sensor Networks［J］. IEEE Transactions on Wireless Communications，2011，10（5）：1389-1395.

［14］Bulusu N，Heidemann J，Estrin D.GPS-Less Low Cost Outdoor Localization for Very Small Devices［J］.IEEE Personal Communications Magazine，2000，7（5）：28-34.

［15］袁鑫，吴晓平，王国英.线性最小二乘法的RSSI定位精确计算方法［J］.传感技术学报，2014，27（10）：1412-1417.

［16］刘志华，李改燕，刘晓爽.基于最小二乘法的蒙特卡洛移动节点定位算法［J］.传感技术学报，2012，25（4）：541-544.

［17］吕振，赵鹏飞.一种改进的无线传感器网络加权质心定位算法［J］.计算机测量与控制，2013，21（4）：1102-1104.

［18］刘运杰，金明录，崔承毅.传感器网络修正加权质心定位算法［J］.传感技术学报，2010，23（5）：717-721.

［19］张橙，宋学瑞.基于ZigBee的RSSI测距方精度研究［J］.湖南工业大学学报，2011，25（5）：37-41.

赵大龙（1987-），男，河北省保定市人，硕士研究生，现就读于内蒙古大学电子信息工程学院，主要研究方向为无线传感网络，zhaodl1987@163.com；

白凤山（1963-）男，教授，内蒙古呼和浩特市人，现在内蒙古大学电子信息工程学院工作，主要研究方向无线通信、无线传感网络等，eefs8015@163.com。

An Improved Triangle Centroid Location Algorithm Based on Kalman Filtering and Linear Interpolation*

ZHAO Dalong，BAI Fengshan*，DONG Siyu，LI Hongshu
（College of Electronic and Information Engineering，Inner Mongolia University，Hohhot 010021，China）

The target location technology based on RSSI with the features of low complexity and high locating accuracy has been widely applied to nodes location in WSN.For further improving moving target locating accuracy the optimized RF parameter A and signal transmission constant n in wireless channel model are calculated firstly through RSSI real values received from reference nodes made up of CC2530.Then a more precise estimated distance value between reference and location nodes can be achieved via Kalman filtering and linear interpolation for compensating random errors.Finally an improved triangle centroid location algorithm was tested and simulated on basis of above-mentioned distance value.The simulation results showed that the improved algorithm used in the paper achieved an average about 0.7 m location precision in the testing environment，which is markedly better than that of the existing location algorithms.

wireless moving target location；RSSI；Kalman filtering；linear interpolation；triangle centroid location EEACC：7230

TP212.9；TN393

A

1004-1699（2015）07-1086-05

10.3969/j.issn.1004-1699.2015.07.024

项目来源：内蒙古自治区教育厅研究生科研创新项目（1402020201324）

2014-12-09 修改日期：2015-03-25