一种基于CKF的无线传感器网络分布式定位算法
2015-11-18余木琪
余木琪,邓 平
(西南交通大学信息编码与传输重点实验室,成都 610031)
一种基于CKF的无线传感器网络分布式定位算法
余木琪,邓 平*
(西南交通大学信息编码与传输重点实验室,成都 610031)
为提高无线传感器网络节点定位的精度,降低算法计算复杂性,提出了一种基于容积卡尔曼滤波的无线传感器网络分布式节点定位算法。该算法假定移动锚节点按预定路径在传感区域移动,并周期性广播自身位置信标信息;每个未知位置节点首先收集多个锚节点信标信息及信号强度信息,然后估算出锚节点信标位置与未知节点的距离,最后在未知节点上运用容积卡尔曼滤波算法完成自身位置的分布式定位。仿真结果表明:本文所提算法具有优良的定位性能,定位精度和无迹卡尔曼滤波算法相当,明显优于极大似然估计定位算法,而计算复杂性则低于无迹卡尔曼滤波算法。
无线传感器网络;容积卡尔曼滤波;定位;移动锚节点
无线传感器网络(Wireless Sensor Networks,WSN)是由布置在监测区域内大量的廉价微型传感器节点组成,通过无线通信方式形成的一个多跳自组织网络,其目的是协作地感知、采集和处理网络覆盖区域中监测对象的信息,并发送给观察者[1]。无线传感器网络涉及传感器技术、微机电系统、现代网络和无线通信等技术,是21世纪最重要的新兴技术之一,也是目前IT领域中的研究热点之一[2]。在无线传感器网络中,节点的位置信息对网络的监测活动至关重要。
近年来,无线传感器网络节点定位技术得到飞速发展,主要的定位算法有测距定位、非测距定位、凸优化、移动锚节点定位、蒙特卡洛定位(Monte Caro localization,MCL)等算法[3-5]。文献[5]中Lingxuan Hu和David Evans参考移动机器人中的序列蒙特卡洛定位方法的思想,首次将MCL应用于移动传感网的定位中,但是该算法需要很高的锚节点密度才能获得比较好的定位精度,计算复杂度高,且不能应用于节点静止的无线传感器网络的节点定位。文献[6]中Liqiang Zhang等人将目标跟踪的过程运用于移动锚节点的无线传感器网络分布式定位,提出一种新的分布式传感器定位算法。该算法运用无迹卡尔曼滤波(Unscented Kalman Filter,UKF)进行定位,能取得较高的定位精度,但是UKF算法的可调参数选取不好会使其不稳定。文献[7]对文献[6]的初始位置选取进行改进,首先接收三个不共线的锚节点信标信息,运用三边测量法定位出未知节点的粗略初始位置,再运用UKF算法完成定位。该算法在锚节点发送信标信息密集时出现局部线性,使得该算法长时间选取不到不共线的信标,无法及时得到初始位置,进而使得运行时间过长。
容积卡尔曼滤波(Cubature Kalman Filter,CKF)是Ienkaran Arasaratnam和Simon Haykin于2009年提出的一种滤波估计精度高、稳定性好、计算量小的非线性滤波方法[8-9]。近年来有许多研究者对CKF算法进行改进,并应用于列车导航定位、目标跟踪等领域,但目前还未见到研究者将其应用于无线传感器网络节点定位中。
本文借鉴Liqiang Zhang等人所提算法的思想,将容积卡尔曼滤波运用于无线传感器网络节点定位中,提出一种基于容积卡尔曼滤波的无线传感器网络节点分布式定位算法。该算法的主要步骤为:移动锚节点按预定路径在传感区域移动,并周期性广播自身位置信息;每个未知位置节点首先收集锚节点位置信息及对应的信号强度信息,然后估算出锚节点与未知节点的距离,最后在未知节点上运用CKF算法完成自身位置的定位。
本文首先给出移动锚节点定位模型,然后分析了容积卡尔曼滤波算法的特点,给出了详细的算法步骤,接着详细介绍了基于CKF的WSN节点分布式定位的算法流程,最后建立仿真环境,仿真分析了测距误差、锚节点信标个数、初始位置对本文算法定位精度的影响,并与文献[6]所提UKF算法及极大似然估计定位法的性能进行了仿真比较。
1 移动锚节点定位模型
假设无线传感器网络中有N个传感器节点,第i (i=1,…,N)个传感器节点在k时刻的系统状态为Xi(k)=[Xi1(k),Xi2(k),Xi3(k)]T。本文考虑静止的传感器节点,则移动锚节点定位系统的状态方程和观测方程如下:
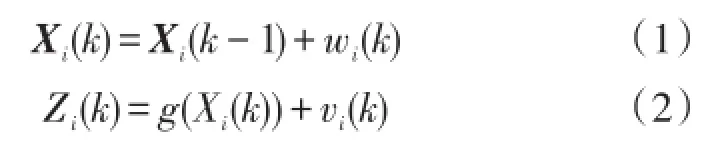
取传感器节点i在k时刻与移动锚节点之间的距离作为观测量,
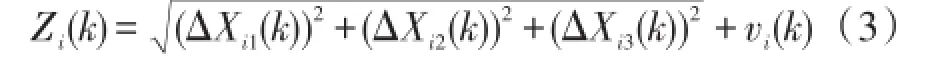
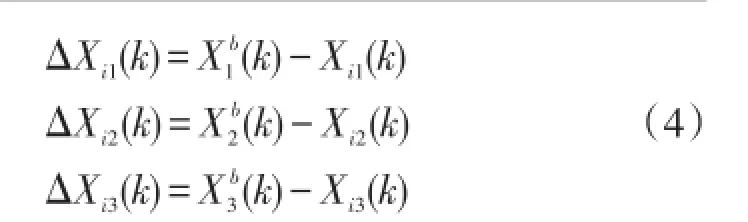
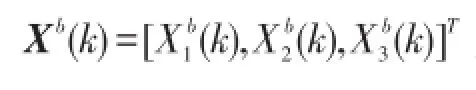
2 容积卡尔曼滤波算法
卡尔曼滤波是最经典的滤波估计方法,但只适用于线性观测方程,扩展卡尔曼滤波(Extended Kalman Filter,EKF)是传统处理非线性方程的滤波估计方法,EKF能够达到一阶泰勒展式的精度,但在非线性度偏高的场合会出现滤波发散[10]。无迹卡尔曼滤波是一种求sigma点的非线性滤波方法,该算法精度高,能够达到二阶甚至三阶泰勒展式的精度,但是该算法的主要弱点是不稳定[11]。
容积卡尔曼滤波算法的基本思想仍然是一种“预测—校正”的经典卡尔曼滤波结构下的估计算法,它与EKF、UKF相同,同属于高斯域贝叶斯滤波的结构范畴,但是CKF因其实现简单、非线性逼近特性强等优点,在与传统非线性算法策略的比较中具有极大的优势。CKF采用了UKF类似的点集近似分布方法,能够获得比EKF更高的非线性逼近性能[12],当UKF的参数κ=0时,CKF 与UKF的滤波性能一致[13-14]。相比于UKF,CKF具备的主要优势有[12]:对三维以上的状态方程,滤波精度更高,可采用平方根策略求解,滤波稳定性更优。
容积卡尔曼滤波算法的基本步骤如下。
2.1 时间更新
①假设在k-1时刻的估计方差已知,对其分解得

②计算Cubature点
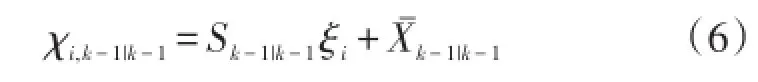
③计算更新后的Cubature点
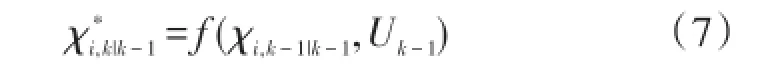
④计算一步预测状态
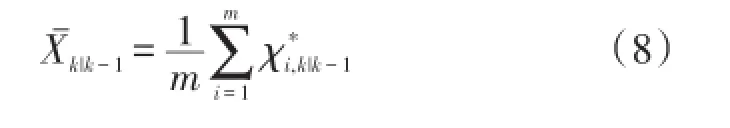
⑤计算一步预测误差方差
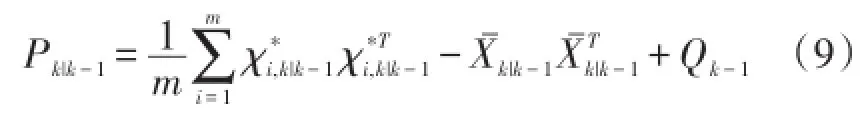
2.2 测量更新
①对一步预测误差方差进行分解
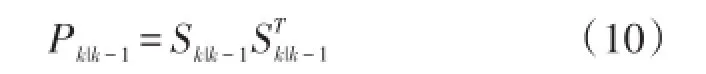
②计算cubature点
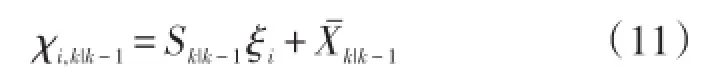
③计算通过量测方程的Cubature点
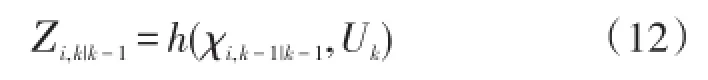
④计算量测估计值
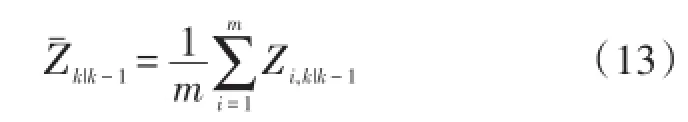
⑤计算更新后的量测误差方差

⑥计算协方差

⑦计算卡尔曼滤波增益
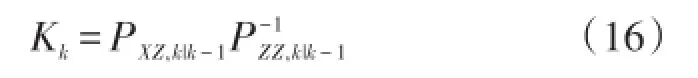
⑧ 计算更新后的状态
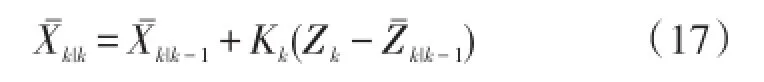
⑨ 计算相应的估计误差方差
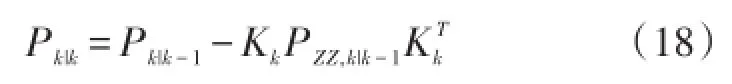
3 基于CKF的WSN节点定位算法
在无线传感器网络中,移动锚节点按规定的移动路径在传感区域移动,周期性广播自身位置信息,每个未知节点收集锚节点位置信息并计算出锚节点与未知节点的距离,对每个未知节点独立运用容积卡尔曼滤波定位出自身位置坐标。该算法的流程图如图1所示。
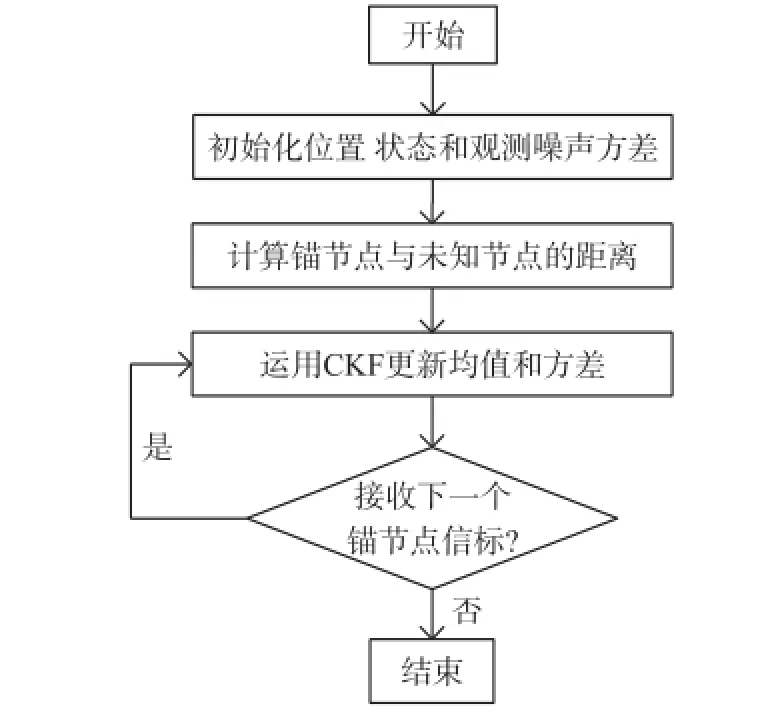
图1 基于CKF的WSN节点定位算法流程图
4 定位性能仿真分析
[6]的仿真场景,本文假设在1 000 m×1 000 m的传感区域内随机布置N=200个传感器节点。假设所有未知位置节点进行迭代估计的初始位置设置为传感区域的中心,即x(0)=(500,500),假设状态过程噪声方差矩阵为Q=diag([0.001,0.001,0.001]),测 距 误 差 为range_error=10%,观测噪声方差为 R=(700*2* range_error)2*sc,其中sc表示观测噪声方差放大因子,假设 sc=0.01,初始位置噪声方差矩阵为P=100*diag([1,1,1]),取迭代次数,即移动锚节点广播信标的个数为100,以下仿真中若未做特殊说明,初始条件不变。移动锚节点在距离传感区域100 m高的平面按圆心为(500 m,500 m)、半径为700 m的圆形路径移动,该圆形覆盖了整个传感区域。锚节点每圈广播信标个数为beacons_per_round=15,在该仿真场景中,移动锚节点在k时刻的坐标表示为
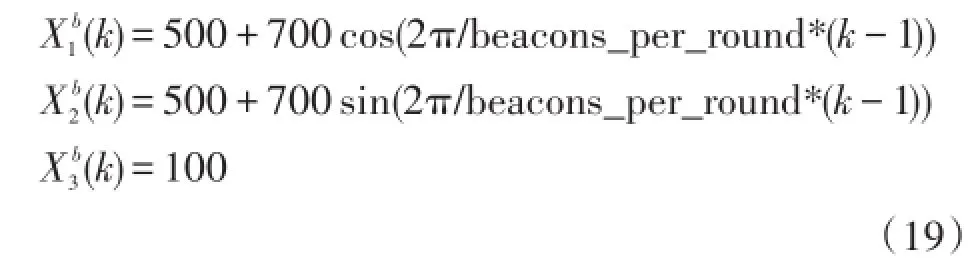
假设距离测量值的误差主要由高斯噪声引起,则测量距离与真实距离之间的关系表示如下:
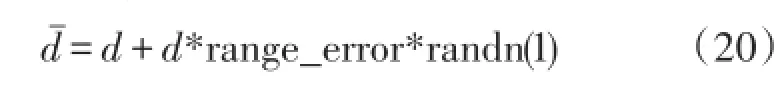
其中dˉ为测量距离,d为真实距离,range_error为[0,1]之间的一个固定值,randn(1)是标准的正态随机变量。
本文选取平均定位误差(Mean Positioning Error,MPE)作为定位精度评价标准,定义:位置节点的真实位置
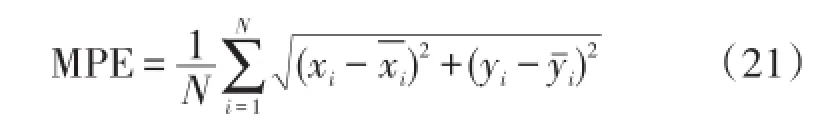
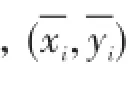
算法的计算复杂性,即时间复杂度,是指执行算法所需要的计算工作量,它定量描述了该算法的运行时间,决定了算法的运行时间长短,即计算复杂性越低,运行时间越短,算法性能越优。本文选取算法的运行时间作为计算复杂性的评价标准。
4.1 测距误差对定位精度的影响
测距的精确度对无线传感器网络节点定位有很大的影响,通常测距精度越高,定位的精度也越高,反之,测距精度越低,定位的精度也越低。本次仿真选取4种不同的测距误差,range_error分别为5%、10%、15%、20%。仿真得出测距误差对定位精度的影响如图2所示。
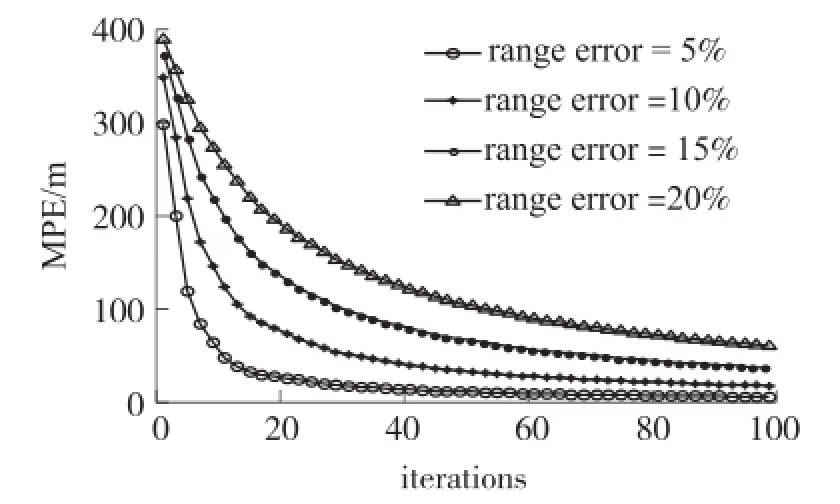
图2 测距误差对定位精度的影响
由图2可以看出锚节点信标个数相同的情况下,随着测距误差的增加,定位精度降低。
4.2 锚节点信标个数对定位精度的影响
由图2可以看出,随着锚节点信标个数的增加,定位精度增高。然而,锚节点过多不仅会增加通信负荷,而且会加大每个传感器节点的运算量。本节研究锚节点信标总数相同的情况下,锚节点每圈广播信标个数对定位精度的影响。设置锚节点每圈广播信标个数分别为15、60、240时,锚节点信标个数与定位精度的关系如图3。
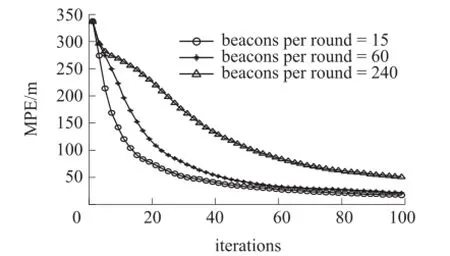
图3 锚节点每圈广播信标个数对定位精度的影响
由图3可以看出锚节点总数固定的情况下,锚节点每圈广播个数越少,定位精度越高,这主要是几何精度因子对定位所产生的影响。
4.3 初始位置对定位精度的影响
初始参数对卡尔曼滤波的性能有着不可忽视的影响,不同的初始位置、位置方差、观测噪声方差、状态噪声方差都会对定位产生很大的影响。本次仿真取三边测量法估计的初始位置、传感区域的圆心(500,500)、圆外(1210,500)。图4为不同的初始位置对定位精度的影响。
由图4可以看出先运用三边测量法估计出未知位置节点的粗略初始位置,再进行CKF迭代,其定位精度明显高于于初始位置在圆心和圆外。

图4 初始位置对定位精度的影响
4.4CKF、UKF、MLE定位算法比较
图5仿真了CKF、UKF、MLE三种定位算法的定位精度比较。由图5可以看出,CKF和UKF运用于无线传感器网络节点定位,具有相同的定位精度,且高于MLE。图6为对基于CKF的WSN节点定位算法和基于UKF的WSN节点定位算法分别进行50次蒙特卡洛仿真,得出的运行时间比较图,本次仿真采样的锚节点信标总数为50个,仿真环境为Windows XP系统下的MATLAB R2010(a)。由图6可以看出,CKF算法的运行时间低于UKF算法,即CKF算法的计算复杂性低于UKF算法。
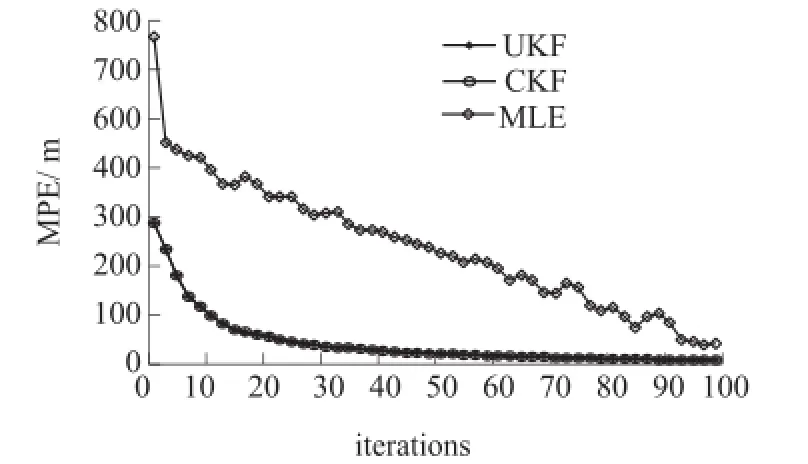
图5 UKF、CKF、MLE的定位精度比较
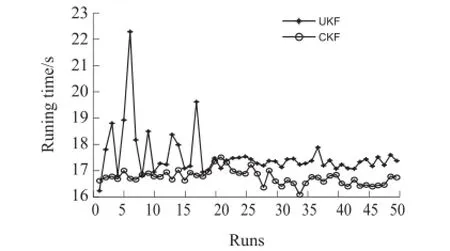
图6 CKF、UKF运行时间比较
5 结论
本文研究无线传感器网络节点定位问题,提出一种基于容积卡尔曼滤波的无线传感器网络分布式定位算法。该算法无需节点间通信,具有较高的定位精度和较低的计算复杂性。仿真验证了本文算法的定位精度与UKF算法相同,明显优于极大似然估计定位算法,而计算复杂性则低于UKF算法。
参考文献:
[1] Akyildiz I F,Su W,Sankarasubramaniam Y,et al.Wireless Sensor Networks:A Survey[J].Computer Networks,2002,38(4):393-422.
[2] Chong C Y,Kumar S P.Sensor Networks:Evolution,Opportunities,and Challenges[C]//Proceedings of the IEEE,2003:1247-1256.
[3] 何国刚,邓平.一种高斯噪声下基于最大分散度的WSN半定规划定位算法[J].传感技术学报,2012,25(8):1004-1699.
[4] 王静,邓平.一种基于边松弛的大规模WSN分簇定位算法[J].传感技术学报,2013,26(5):683-688.
[5] Lingxuan Hu,David Evans.Localization for Mobile Sensor Networks[J].MobiCom'04,2004:45-57.
[6] Zhang Liqiang,Cheng Qiang,Wang Yingge,et al.A Novel Distributed Sensor Positioning System Using the Dual of Target Tracking [J].IEEE Transactions on Computers,2008,57(2):246-260.
[7] Hu Weiwei,Qin Huibin,Huang Haiyun.A Mobile Beacon Based Method for Wireless Sensor Networks Localization[C]//IEEE International Conference on Communication Technology Proceedings,2008:144-147.
[8] Ienkaran Arasaratnam,Simon Haykin.Cubature Kalman Filters [J].IEEE Transaction on Automatic Control,2009,54(6):1254-1269.
[9] Ienkaran Arasaratnam,Simon Haykin,Thomas R Hurd.Cubature Kalman Filtering for Continuous-Discrete Systems:Theory and Simulations[J].IEEE Transactions on Signal Processing,2010,58 (10):4977-4993.
[10]Fred Daum.Nonlinear Filters:Beyond the Kalman Filter[J]. IEEE A&E Systems Magazine,2005,20(8):57-69.
[11]Simon J Julier,Jeffrey K Uhlmann.Unscented Filtering and Nonlinear Estimation[C]//Proceedings of the IEEE,2004,92(3):401-422.
[12]蔡伯根.低成本列控系统的列车组合定位理论与方法[D].北京:北京交通大学,2010:54-58.
[13]Chang Lubin,Hu Baiqing,Li An,et al.Transformed Unscented Kalman Filter[J].IEEE Transactions on Automatic Control,2013,58(1):252-257.
[14]孙枫,唐李军.Cubature卡尔曼滤波与Unscented卡尔曼滤波估计精度比较[J].控制与决策,2013,28(2):303-308.

余木琪(1989-),男,汉族,硕士研究生。主要从事无线传感器网络定位跟踪技术的研究;

邓 平(1964-),男,汉族,博士,教授。主要研究方向有无线网络定位技术,现代信号处理,无线传感器网络等。
A Distributed Localization Algorithm Based on Cubature Kalman Filter in Wireless Sensor Networks
YU Muqi,DENG Ping*
(Key lab of information coding and transmission,Southwest JIAOTONG University,Chengdu 610031,China)
To improve the localization accuracy and decrease the computation complexity,a distributed node localization algorithm based on cubature kalman filter in wireless sensor networks is proposed.The algorithm supposes that a mobile beacon moves by predetermined trajectory around a sensor field,and periodically broadcasts its current location.Each sensor collects the location and RSS of beacons,measures the distance between itself and the beacon,and individually calculates their locations via a Cubature Kalman Filter algorithm.Simulations show that the proposed algorithm has a good localization performance,the localization accuracy is same to the UKF algorithm,better than the MLE localization algorithm,and the computation complexity is smaller than the UKF algorithm.
WSN;CKF;localization;moving beacon EEACC:7230
TP393
A
1004-1699(2015)07-1041-05
10.3969/j.issn.1004-1699.2015.07.017
2015-01-30 修改日期:2015-03-09
