压力传感器测试系统的动态校准及特性分析

轩春青，轩志伟，赖富文

（1.郑州成功财经学院，信息工程系，河南巩义 451200；2.郑州大学信息工程系，郑州 450001；3.中北大学，电子测试技术国防重点实验室，太原 030051；4.武汉高德红外股份有限公司，武汉 430070；5.中国白城兵器实验中心，吉林白城 137001）

压力传感器测试系统的动态校准及特性分析

轩春青1，2*，轩志伟3，4，赖富文3，5

（1.郑州成功财经学院，信息工程系，河南巩义 451200；2.郑州大学信息工程系，郑州 450001；3.中北大学，电子测试技术国防重点实验室，太原 030051；4.武汉高德红外股份有限公司，武汉 430070；5.中国白城兵器实验中心，吉林白城 137001）

针对利用传感器静态灵敏度对动态信号进行测试时而引入的测量误差，使用激波管对压力传感器进行动态标定，对校准结果进行分析得到传感器的动态特性，并计算出其动态灵敏度。利用校准数据对传感器模型的阶数进行判别，为以后对测试结果进行修正和补偿提供理论依据；最后对动态校准过程中误差的来源进行分析并给出传感器动态灵敏度的不确定度。

传感器动态标定；动态灵敏度；传感器阶次判别；激波管

冲击波压力作为评估战斗部或炸药爆破威力的重要手段，一般是通过压力传感器对爆炸产生的冲击波进行测试而获取的，利用传感器获得的地面反射压力可以推算出爆炸波的当量。由于爆炸冲击波属于动态变化的信号，使用压力传感器厂家提供的静态灵敏度对测试结果进行计算时，不可避免地带来计算误差，严重影响动态测试的精度。为了测得更加精确的冲击波威力，使压力传感器能给出更准确的测试结果，在具体试验前必须对传感器进行动态标定［1-3］，并对传感器系统进行建模分析。

在所有的动态压力标定装置中，激波管具有上升前沿陡峭、激波持续时间长、能充分激励起传感器的动态特性等优点，在压力传感器的动态参数校准中得到了广泛的应用。此外，对用于爆炸冲击波威力测量的压力传感器进行动态标定时，激波管的冲击波前沿与爆炸冲击波前沿类似测试系统的工作状态和实际情况基本一致，能更好的反应系统在工作时的特性。

1 激波管校准压力测试系统的原理

压力传感器测试系统的动态特性主要包括动态数学模型和动态性能指标等。动态性能指标包括上升时间、过冲（超条量）、峰值时间、阻尼比等；频域性能指标为通频带、谐振频率、工作带宽等。

压力传感器一般等效为二阶系统，现有的传感器受制作工艺等条件的限制，工作频带窄于信号的频谱，在冲击波信号的激励下，传感器输出的信号将在谐振点处发生震荡，引入动态误差。为了使测试结果更加精确，必须根据传感器的模型对测试结果进行补偿，以提高测试精度［2］。根据传感器对输入激励的响应，通过最小二乘法识别出最接近传感器模型的阶次作为传感器的动态模型。

为了准确获取传感器系统的动态特性，使用激波管对传感器系统进行充分激励。标定时，将压力传感器齐平安装在激波管末端端面上，如图1所示。在激波管阶跃压力信号的激励下，传感器将会产生振荡；使用采集卡对传感器的输出进行采集。对得到的数据进行分析，确定传感器的上升时间、谐振频率以及过冲量等各项动态特性指标。并通过输入阶跃信号压力值和传感器响应输出的稳定值计算出压力传感器的动态灵敏度，如式（1）所示：

式中：S为压力传感器的动态灵敏度；Vo为压力传感器输出的稳定值；Ps为输入阶跃信号压力值。

图1 激波管动态校准系统原理图

整个标定系统由激波管、多通道采集卡、测速传感器、信号调理采集电路、被标定传感器、高压空气瓶等组成。实验中所用激波管可以标定压电压力传感器的动态响应性能，标定激波管的主体为高压室和低压室两部分，中间使用膜片隔开。两室压差达到某一定值时，膜片破裂，高压室气体冲向低压室形成入射激波。多通道采集卡准确记录激波到达各个测速传感器的时间，测速传感器之间的间距为d cm，故激波速度Vs如式（2）所示：

因传感器安装在激波管末端，承受的是反射激波阶跃压力Ps，其计算公式如式（3）所示：

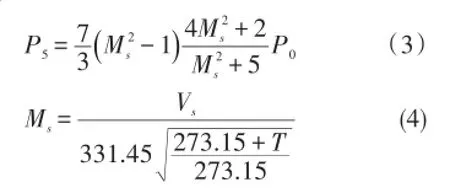
式中：P5为激波的反射超压，P0为低压室气体初始压力；Ms为激波入射时的马赫数，T是空气温度。传感器的输出电压值Vo可以通过调理采集电路直接获得。将P5和Vo直接带入式（1），即可求得传感器的动态灵敏度。

2 标定方法及动态特性分析

测试系统的动态特性不仅与传感器有关，还受调理电路等的影响。为了获取系统的实际动态特性，将传感器与信号调理电路作为一个整体进行动态标定。本次试验选用PCB公司的压阻型的压力传感器，其谐振频率在2 000 kHz～300 kHz之间。传感器安装在激波管末端，信号调理电路为自制采集存储电路，与传感器一起构成测试系统。因压力传感器为小阻尼线性系统，在阶跃信号的激励下会产生一个振幅衰减的振荡信号，为了保证动态校准的准确度，输入阶跃压力信号必须保持到传感器输出振荡信号结束后的一段时间，压力传感器动态校准中规定的激波阶跃压力的平台持续时间应大于4 ms，文中所用激波管阶跃压力的平台持续时间为4 ms～5 ms［4］.

对同一规格的八只传感器进行了标定，每只传感器重复标定三次，得到传感器的动态特性以及其灵敏度，标定结果如表1所示。

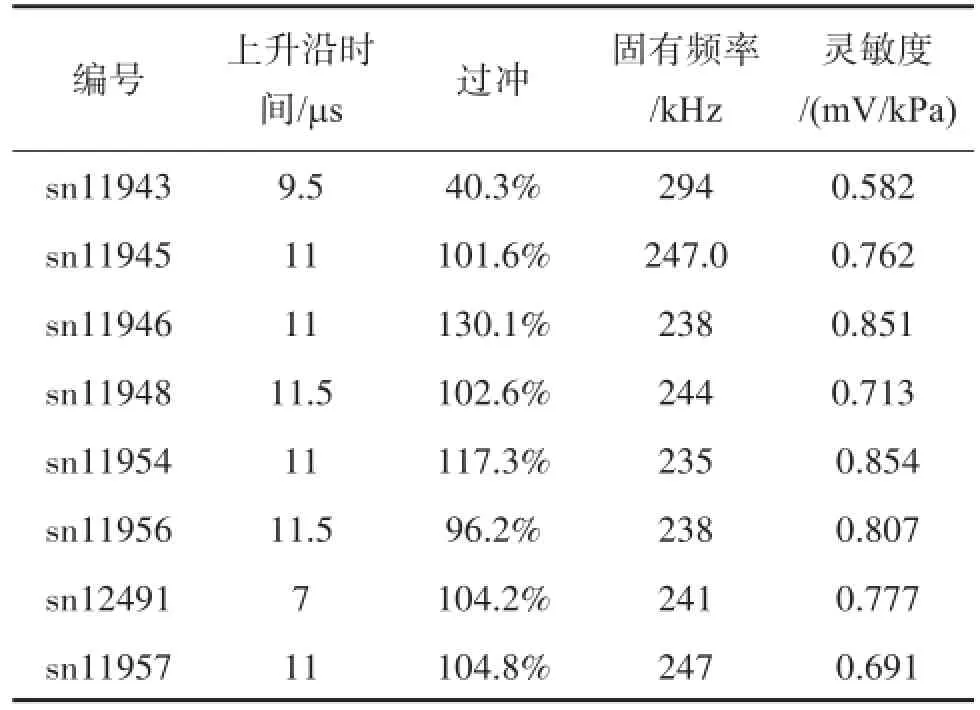
表1 不同压力传感器的动态特性

图2为该传感器在某次激励下的输出响应，如图所示，传感器已被充分的激励起来。过冲量采用传感器输出响应中超出稳定值的最大值差与阶跃响应稳定值之比来表示。为了减少系统过冲量对灵敏度的影响，按压力曲线内外包罗线的平均电压值计算动态灵敏度［5］，根据传感器的输出响应计算出其固有频率为246.9 kHz，上升沿时间、过冲量与动态灵敏度的计算结果表1所示。

图2 传感器阶跃响应波形

与传感器出厂标定的静态灵敏度相比，传感器的动态灵敏度与静态灵敏度存在差异，有着较大的误差。

3 压力传感器的动态模型的确定

压力传感器一般等效为二阶系统，在数据处理中为了获取好的补偿效果，大多将传感器看做具有较高阶次的系统。但是阶次过高，会加大求解补偿器时计算的工作量而对补偿效果改善极小。因此需要对传感器的阶次做必要的验证，精确确定其模型结构。本文利用传感器在阶跃信号激励下的响应数据，根据最小二乘法通过残差的方差来判定系统阶次［6-7］。

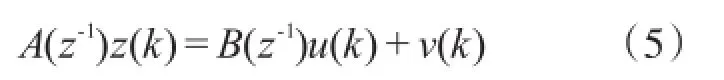
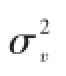
其中n为模型阶次。

模型的最小二乘格式可写成

式中，数据向量和参数向量定义为

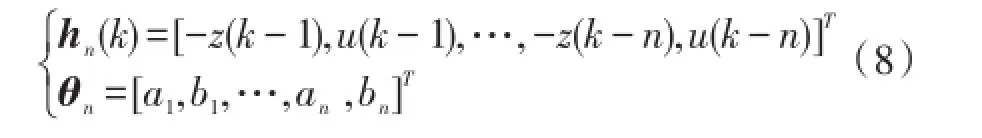
运用最小二乘原理，可获得模型参数θn的最小二乘估计为

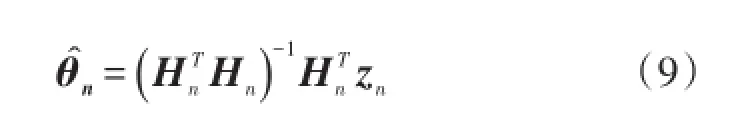
式中，数据矩阵和输出向量定义为

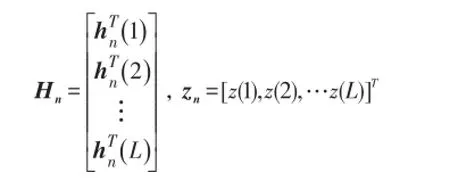
其中，L为数据长度。模型阶次为n时，输出残差向量可写成

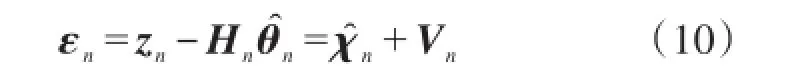
式中

残差的方差为

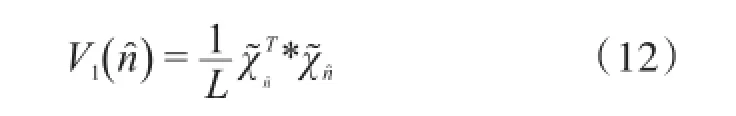
激波管产生的压力信号可以看成是阶跃信号，压力传感器的输出作为对阶跃信号的响应，如图3所示。为了辨识计算的方便，对传感器的输出进行了归一化处理。利用阶跃信号与传感器输出，采用残差方差的方法进行阶次辨识，得到的不同阶次估计时残差的方差的值如图4所示。

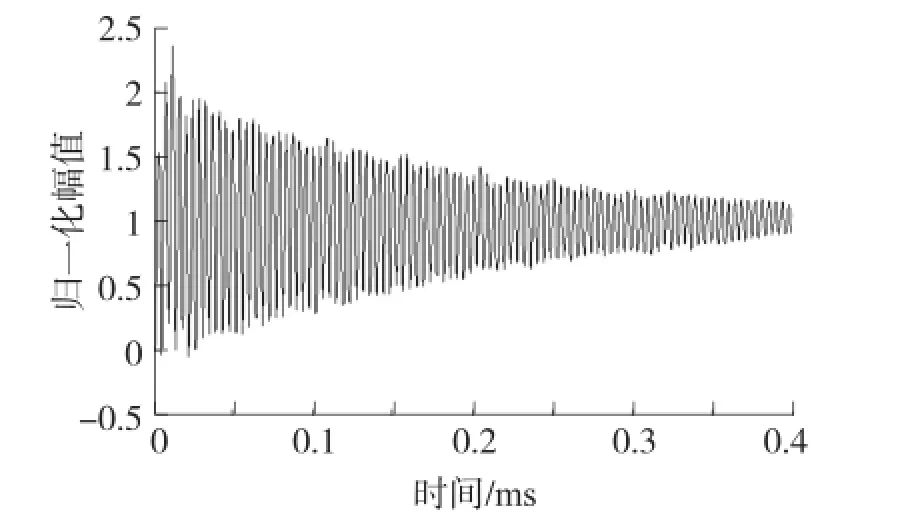
图3 某压力阶跃响应

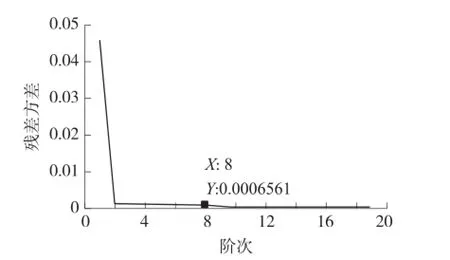
图4 不同阶次残差的方差值

从图4可以看出，残差的方差在n=2时，显著下降，然后开始略微有些下降，由于系统的一些噪声以及传感器结构等，用一个高阶的系统来描述该压力传感器系统会更准确，考虑到后续对传感器输出进行补偿时硬件实现难度问题，选取传感器阶数为八阶［8］。

4 校准结果的不确定度来源分析

测试系统动态特性的不确定度是多次动态校准数据确定的测试系统传递函数、频率特性等的统计结果，它表征了传递函数中各个系数、幅频特性和相角特性的均值估计及在某一置信概率下的变化范围［9-10］.

在校准过程中，不可避免的会存在不确定度，影响到标定的准确性。根据式5可知，传感器动态灵敏度的不确定度主要来源为阶跃压力、压力传感器输出等。由式（6）～式（8）可得：

由式（13）可以看出，反射激波阶跃压力的测量结果主要受大气压力值P0、气体温度T、两个测速传感器的距离d、激波经过两测速传感器的时间t等的影响［11-12］；当各分量不相关时，反射压力P5不确定度为：

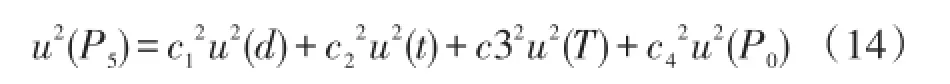
0出电压值的不确定度来源有压力传感器、调理电路误差、读数误差等。其中压力传感器的准确度与调理电路的准确度已知。对测试结果进行多次读数，根据式（12）求得读数误差。

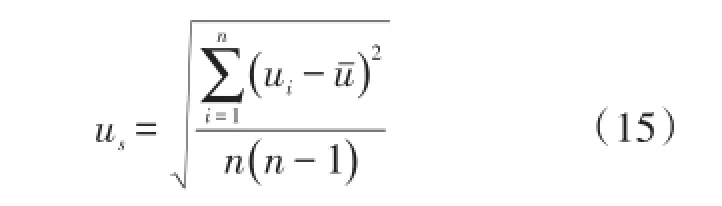
根据式（9）可知传感器动态灵敏度的不确定分量主要有激波压力不确定量和传感器输出电压不确定量组成，如式（16）所示：

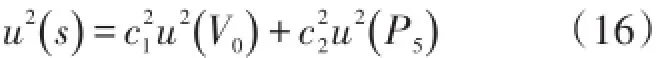
校准实验时温度T为13℃、大气压P0为9.184× 10-2MPa、测速传感器之间的距离d为0.2 m。某次试验时激波经过两个测速探头所用时间为0.4776ms，推算出反射激波压力为139 kPa，激波的马赫数为1.234，传感器输出电压为100.8 mV，传感器的动态灵敏度为0.724 mV/kPa。假设各不确定分量服从均匀分布，根据上述分析可以计算出反射激波压力的合成不确定度为0.007，反射激波相对合成标准不确定度5%。最终求得传感器动态灵敏度的不确定度为4.04×10-2，其不确定度为5.6%。

5 结论

根据动态测试现场的需求采用激波管对压力传感器测试系统进行了动态校准，根据校准结果对测试系统的动态特性如上升时间、过冲、固有频率、灵敏度等进行了分析，利用校准的数据对传感器模型的阶数进行了确立，为以后对测试结果进行修正和补偿提供了理论依据；并分析了动态校准过程中误差的来源；传感器的动态灵敏度与静态灵敏度存在着的差异，在动态测试中对测量结果影响较大，在测量时应使用动态灵敏度以减少误差，提高了测试的准确性。

［1］ 郭炜，俞统昌，李正来，等.冲击波压力传感器灵敏度的动态校准［J］.火炸药学报，2006，29（3）：62-64.

［2］ 张远平，池家春，龚晏青，等.爆炸冲击波压力测试技术及其复杂信号的处理方法［J］.仪器仪表学报，2008，8（28）：325-327.

［3］ 王等旺，张德志，李焰，等.冲击波压杆式传感器测试系统的动态标定［J］.第十二届全国激波与激波管会议论文集，363-366.

［4］ 余尚江，李跃波，曾辉等.基于激波管校准的传感器动态灵敏度试验研究［J］.第十二届全国激波与激波管会议论文集，358-362.

［5］ 崔海涛，刘庆明.冲击波压力传感器测试系统的动态标定［J］.流体力学实验与测量，2004，1（8）：92-96.

［6］ 轩春青，轩志伟，陈保立.基于最小二乘与粒子群算法的压力传感器动态补偿方法［J］.传感技术学报，2014，27（10）：1363-1367.

［7］ 刘一江，孟立凡，张志杰.基于遗传算法的传感器动态特性改善方法［J］.传感技术学报，2013，26（9）：1248-1253.

［8］ 刘一江，孟立凡，张志杰.基于改进RLS的传感器动态特性校正方法［J］.传感技术学报，2013，26（6）：857-860.

［9］ 吴健，张志杰，王文廉.传感器动态误差高速并行修正方法及其FPGA实现术［J］.传感技术学报，2012，25（1）：67-71.

［10］刘帆，杜红棉，范锦彪，等.炮口冲击波超压无线存储测试系统设计［J］.传感技术学报，2014，27（2）：272-276.

［11］孙艳梅，都文和，冯昌浩，等.基于蚁群聚类算法的RBF神经网络在压力传感器中的应用［J］.传感技术学报，2013，26（6）：806-809.

［12］黎小毛，鲁辉，朱宝良.激波管校准压力传感器动态灵敏度不确定度评定［J］.计量技术，2010（6）：45-47.

轩春青（1982-），女，河南周口人，硕士，现任郑州成功财经学院讲师，主要从事数据采集、嵌入式系统等方面的研究，完成省部级课题4项，在国内刊物发表论文20篇，Zhangxuanchunqing@163.com；

赖富文（1973-），男，四川邻水人，中国白城兵器试74验中心高级工程师，主要研究方向武器动态测试，laifuwen0106@ 163.com。

轩志伟（1989-）男，河南周口人，硕士，主要从事动态测试与嵌入式系统等方面的研究，在国内刊物发表论文12篇，shine071201@163.com；

The Dynamic Calibration of Pressure Sensor Test System and Sensitivity Analysis

XUAN Chunqing1，2*，XUAN Zhiwei3，4，LAI Fuwen3，5
（1.Department of Information Engineering，Zhengzhou Chenggong University of Finance and Economics，Gongyi He'nan 451200，China；2.Department of Information Engineering，Zhengzhou University，Zhengzhou 450001，China；3.National Key laboratory for Electronic Measurement Technology，North University of China，Taiyuan 030051，China；4.Wuhan gold infrared Co，Ltd，Wuhan 430070，China；5.Baicheng Ordnance Test Center of China，Baicheng Jilin 137001，China）

Measurement error will be introduced to the result when using the static sensitivity of sensor in dynamic tests.A shock tube is used to make a dynamic calibration for the pressure sensor，and the dynamic characteristics and the dynamic sensitivity of the sensor will be obtained by making analysis for the result.The calibration data were used to distingish the order of the sensor model，which providing theoretical foundation for the test results' correction and compensation.Finally，the source of the errors in the dynamic calibration is analyzed and the uncertainty of the dynamic sensitivity is given.

dynamic calibration of pressure sensor；dynamic sensitivity；the order distingish of the sensor；shock tube EEACC：7230

TP212.9

A

1004-1699（2015）07-0982-05

10.3969/j.issn.1004-1699.2015.07.007

2014-11-25 修改日期：2015-04-07