基于变胞原理的舰炮装填机构刚-柔耦合动力学建模及误差分析

胡胜海，郭春阳，余伟，祁松，孙军超

（1.哈尔滨工程大学机电工程学院，黑龙江哈尔滨150001；2.中国工程物理研究院化工材料研究所，四川绵阳621900）

基于变胞原理的舰炮装填机构刚-柔耦合动力学建模及误差分析

胡胜海1，郭春阳1，余伟2，祁松1，孙军超1

（1.哈尔滨工程大学机电工程学院，黑龙江哈尔滨150001；2.中国工程物理研究院化工材料研究所，四川绵阳621900）

为满足大口径舰炮的发展需求，提出一种基于变胞原理的装填机构。利用变胞原理进行结构设计，并结合机构运动简图对其进行运动描述和原理分析。采用有限元离散方法，将柔性杆划分为若干梁单元，使用混合坐标系描述梁单元的变形，列出柔性杆的动力学方程。应用Hamilton变分原理建立整个装填机构的刚-柔耦合动力学方程，使用Adams和Ansys联合仿真，得到仿真结果：当系统高速大范围运动时，基于变胞原理的装填机构存在较大的供弹误差；在基于变胞原理的大口径装填机构的研究中，应考虑连杆的柔性变形对供弹精度的影响。

兵器科学与技术；变胞原理；装填机构；刚-柔耦合；供弹误差

0 引言

在20世纪50年代，舰炮曾一度随着导弹的出现而被认为是夕阳装备，但是由于大口径舰炮具有射程远、威力大、持续打击能力强、效费比高等诸多优点，近年来再次引起了各国海军的重视［1］。对于舰炮武器系统而言，供弹系统乃舰炮的核心，其性能的好坏直接影响到整个舰炮武器系统作战能力的高低。

变胞机构是20世纪90年代由英国伦敦大学国王学院的Dai等［2］首次提出的一类新型机构。它根据工况变化能够进行自我重组和重构，具有多功能阶段变化、多拓扑结构变化、多自由度变化等特征［3］。变胞机构的提出给机构学的发展注入了新鲜血液，它丰富了机构学的内容和机构设计方法。目前，变胞机构已经取得一定的成果，在国内外也有了一定的热度与影响力，但是涉及的工程应用领域还不是特别广泛、机构描述方法还不是很成熟，有待进一步的发展。本文从结构上首次将变胞机构应用于供弹系统的设计之中，拓展了变胞机构的应用领域，优化了装填机的运动轨迹，兼顾了供弹速率与多弹种兼容供给能力，解决了目前国内外供弹系统存在的不足。

基于变胞原理的装填机构，由装填机直接将炮弹输送到输弹线，并通过输弹机送入炮膛。因此装填机构中装填机的运动精度将直接影响整个供弹系统的可靠性。传统的装填机构设计过程中，对装填机构做刚体假设，并且应用多刚体动力学理论进行计算和仿真，并没有考虑材料的弹性属性。为了提高基于变胞原理的装填机构动力学性能以及供弹误差的计算精确性，本文应用刚—柔耦合动力学理论进行基于变胞原理的装填机构动力学建模和供弹误差分析。

1 基于变胞机构的供弹系统机理

1.1 机构运动描述

舰炮装填机构的主要任务就是将炮弹从接弹位可靠、快捷地输送到输弹位。为了清晰地描述该机构的运动过程，给出机构在构态1、变胞态和构态2状态下的机构运动简图，如图1所示。

图1 机构运动简图Fig.1 Kinematic diagram of mechanisms

装填机构运动过程如下：当驱动滑块处在最下端时，此时机构处于构态1，装填机位于下端的接弹位；当装填机接弹完毕以后，在驱动滑块的驱动下沿基座上固定导槽向上运动，当装填机上端销轴到达自适应导槽和固定导槽交接点处时，机构处于变胞位置；若驱动滑块继续向上运动，则机构转换到构态2，装填机的运动变为绕自适应导轨圆弧中心的转动，直至装填机轴线与摇架基准线平行为止，此时装填机到达输弹位；输弹完毕以后，驱动滑块向下运动。装填机构则先后经历构态2、变胞位置和构态1，并最终回到接弹位置。由此完成一个装填循环。

1.2 原理分析

上文所描述的装填机构，其机构的巧妙之处在于可以实现自动同步和自动变胞。现在结合机构原理示意图分析自动同步和自动变胞的实现原理。

图2中α代表射角，β代表自适应导轨对应的圆心角，γ代表装填机实现同步需要转动的角度，O代表摇架转动中心，O′代表坐标原点，Oc代表摇架基准线，Oh代表水平基准线，Ov代表竖直基准线，F代表装填机所受的力。

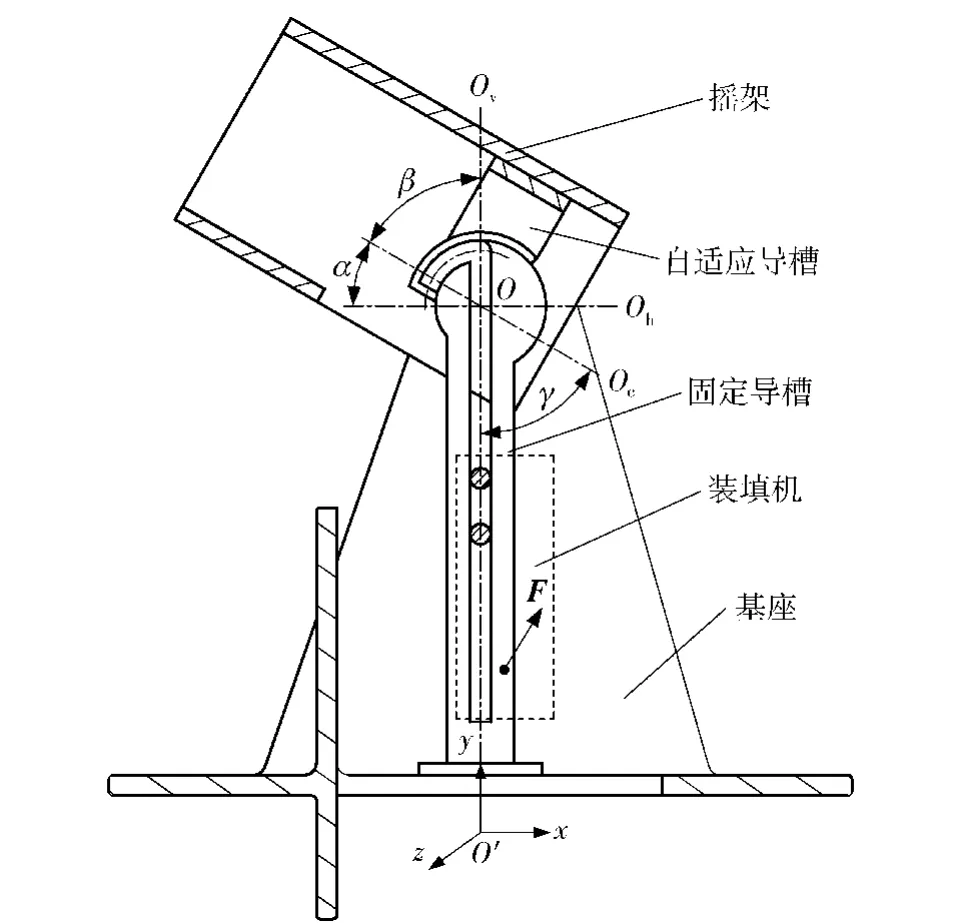
图2 机构原理示意图Fig.2 Schematic diagram of mechanism principle

当射击目标确定以后，摇架就会根据需要调整射角。由于自适应导槽与摇架是固接的，因此自适应导槽与固定导槽组成的自适应导轨会随着射角的变化而自适应变化。且射角α与自适应导轨对应的圆心角β有以下关系：

式中：α为射角，-5°≤α≤90°.

在构态1状态下装填机可以看作一个移动副，在力F的作用下沿固定导槽向上移动。当到达变胞位置时，装填机前端销轴进入自适应导轨段，由此导致了装填机上端销轴所受约束的变化，此时装填机的有效驱动等效力F绕O点产生力矩MO，F与MO有以下关系：

式中：F为一个矢量力；r为矩心O点至力F作用点的矢径。

若MO继续作用，装填机构由构态1变换到构态2，装填机则等效为一个转动副，由此装填机构完成自动变胞。

装填机构的同步是指：装填机轴线与摇架基准线重合。因此要实现装填机构的同步，装填机轴线应由接弹位的竖直基准线Ov转动到输弹位的摇架基准线Oc.装填机实现同步需要转动的角度为竖直基准线Ov与摇架基准线Oc的夹角γ；固定导槽与自适应导槽组成的自适应导轨决定了装填机在装填过程中能绕O点转动的角度。装填机到达输弹位时前端销轴与自适应导槽挡边接触，装填机受机械限制自动停止运动，此时装填机转过的角度为自适应导轨对应的圆心角β.从图2易知：

装填机能自动转动的角度β等于装填机实现同步需要转动的角度γ，因此实现了装填机构的自动同步。

2 基于变胞机构的刚-柔耦合动力学建模

为了更加准确的对基于变胞原理的装填机构的动力学特性进行分析，计入杆的柔性效应。对机构的动力学模型做出如下假设：

1）连杆的材料均匀，各向同性，其本身满足虎克定律；

2）炮弹在装填机内可靠定位，即在装填过程中不存在晃动；

3）炮弹和装填机的整体重心在装填机的正中心。

图3 机构示意图Fig.3 Schematic diagram of mechanisms

如图3所示，滑块的重心位置为M，连接杆和装填机的铰接点为N，装填机和炮弹的重心位置为Q，装填机的转动半径为R，装填机在进入变胞态后转动的角度为q，连杆和水平线的角度为θ，装填机的重心和与连杆铰接中心的垂直距离为e，装填机和炮弹的总质量为mtot，连杆的长、横截面积、横截面对中性轴的惯性矩、密度和弹性模量分别为l、A、I、ρ、E，滑块的质量、进入变胞态前滑块和装填机重心之间垂直距离分别为ms和h.图4为梁的变形示意图，其中Ox0y0为惯性坐标系，Oxy为浮动坐标系［4］。

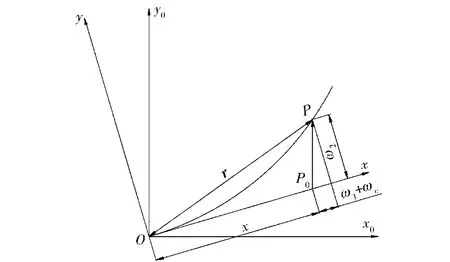
图4 梁的变形示意图Fig.4 Schematic diagram of beam deformation

2.1 柔性杆的动力学方程

梁单元上任意P0点变形后到达P点。变形后的P点位置矢量为

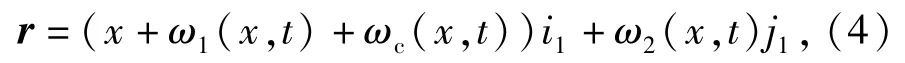
式中：ω1（x，t）为P0点变形后到达P点而引起梁的轴向伸长量；ω2（x，t）为横向弯曲变形量；ωc（x，t）为横向弯曲变形引起的梁的纵向缩短量，称为耦合变形量。传统的零次近似刚-柔耦合模型在建模过程中直接套用了结构动力学中的小变形假设，忽略了耦合变形量ωc（x，t）.当大范围运动为高速时，ωc（x，t）对系统的动力学特性将产生重要影响。ωc（x，t）［5-6］表示为

根据连续介质力学理论，在浮动坐标系下P0点变形后到达P点的变形矢量u［7］为

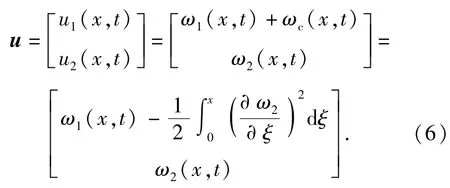
将柔性杆划分为n个梁单元，则柔性杆有（n+ 1）个节点。单元i的长度为Li，单元坐标系Ox1y1在浮动坐标系的位置用其第一个节点在浮动坐标系中的位置xi来表示，杆有限元离散的模型如图5所示。通过单元形函数将单元i内任意点P的变形量ω1和ω2表示为节点变形坐标的线性插值［8］：

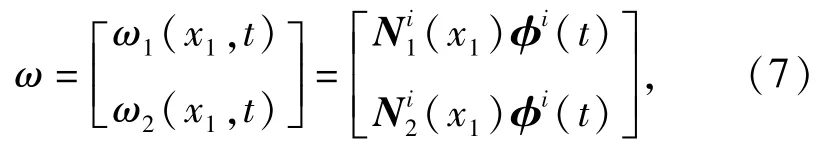
式中：x1表示单元i中任意点P在单元坐标系下的横坐标；为等参单元形函数；φi（t）∈R6×1为单元节点的变形坐标列阵。

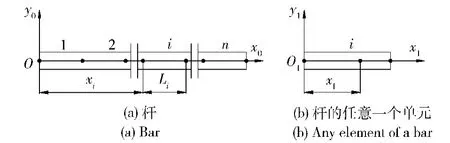
图5 杆有限元离散的模型Fig.5 Finite element discrete model of rod

单元i的形函数Ni可表示为

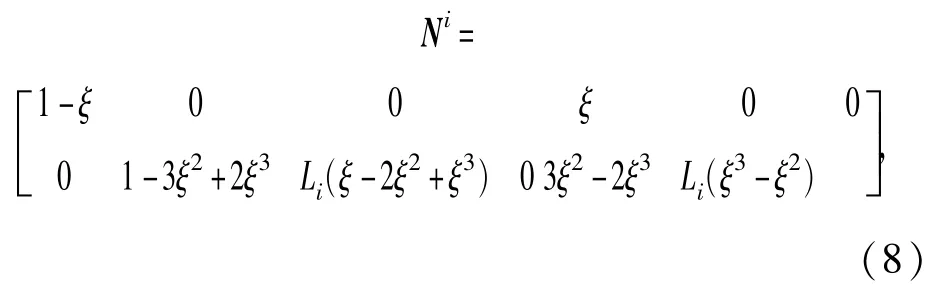
选取广义坐标

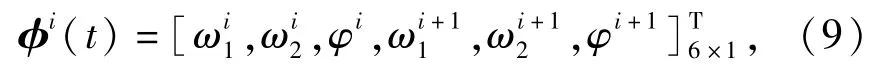
设φi（t）∈R3（n+1）×1为总体的变形矩阵，表示为

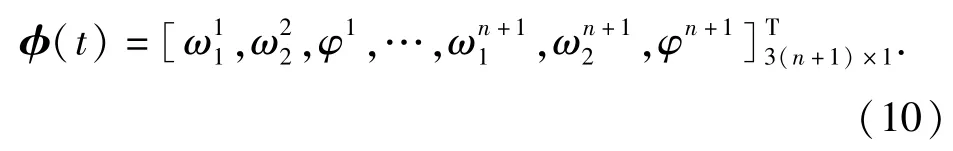
则单元i的节点位移为列阵可表示为

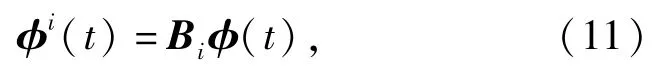
式中：Bi∈R3（n+1）×1为由单元编号决定的布尔指示矩阵，表示如下：

式中：I3∈R3×3为单位阵。将（8）式带入（4）式中，可以得带单元的变形量

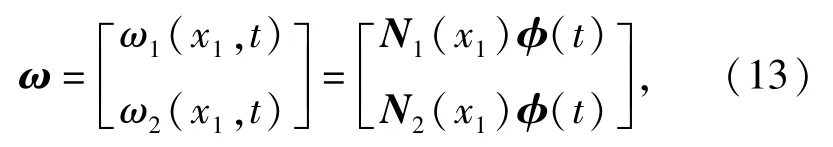
将（10）式代入（3）式，可得第i个单元上点P在浮动坐标系下的位移列阵为

式中：T（i，x1）∈R3（n+1）×3（n+1）为第i个单元的耦合形函数阵，为对称和非负定矩阵，表示为

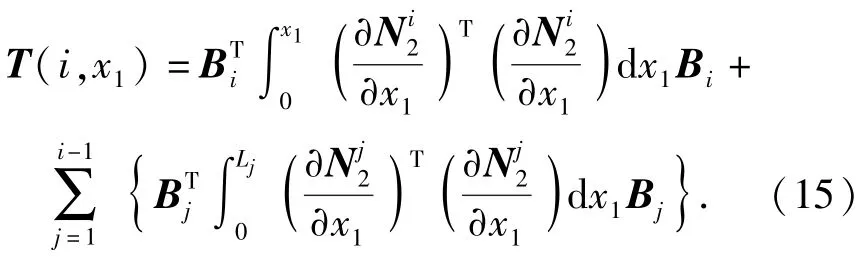
离散后的第i个单元的动力学方程可表达为

Y是柔性杆的广义坐标矩阵，整个柔性杆的动力学方程为

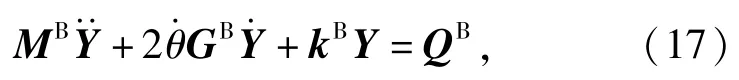
式中的变量表达如下：

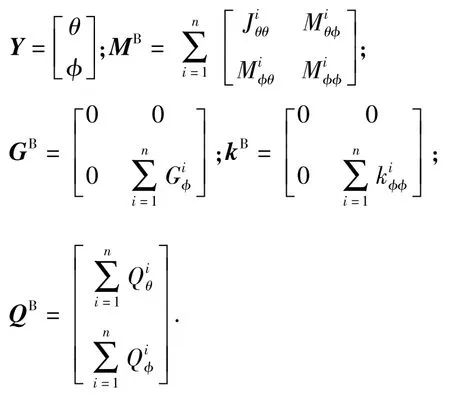
2.2 整个刚-柔耦合系统的动力学方程

在构态1时，装填机沿垂直轨道运动，杆的柔性对其精度影响较小，因此主要对构态2进行分析。应用Hamilton原理建立刚-柔耦合系统的动力学方程

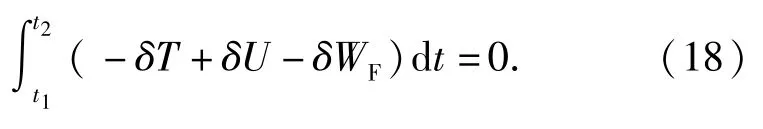
式中：T为系统的总动能；U为系统的势能；WF为外力所做的功。

系统的动能T主要由3部分组成：滑块的动能Ts、柔性杆的动能Tf、装填机和炮弹的动能Ttot，系统的动能T可表示为

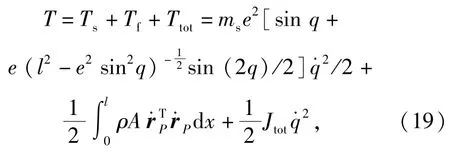
取装填机和炮弹的重心位置的重力势能为0，系统的势能V主要由3部分组成：滑块的势能Vs、柔性杆的势能Vf、装填机和炮弹的势能Vtot，柔性杆的势能包括拉压势能、弯曲势能以及重力势能，系统的动能V可表示为

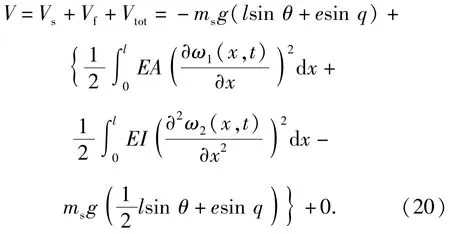
外力所做的虚功为作用在滑块上的外力F所做的虚功，可表示为

系统的动力学方程可表示为

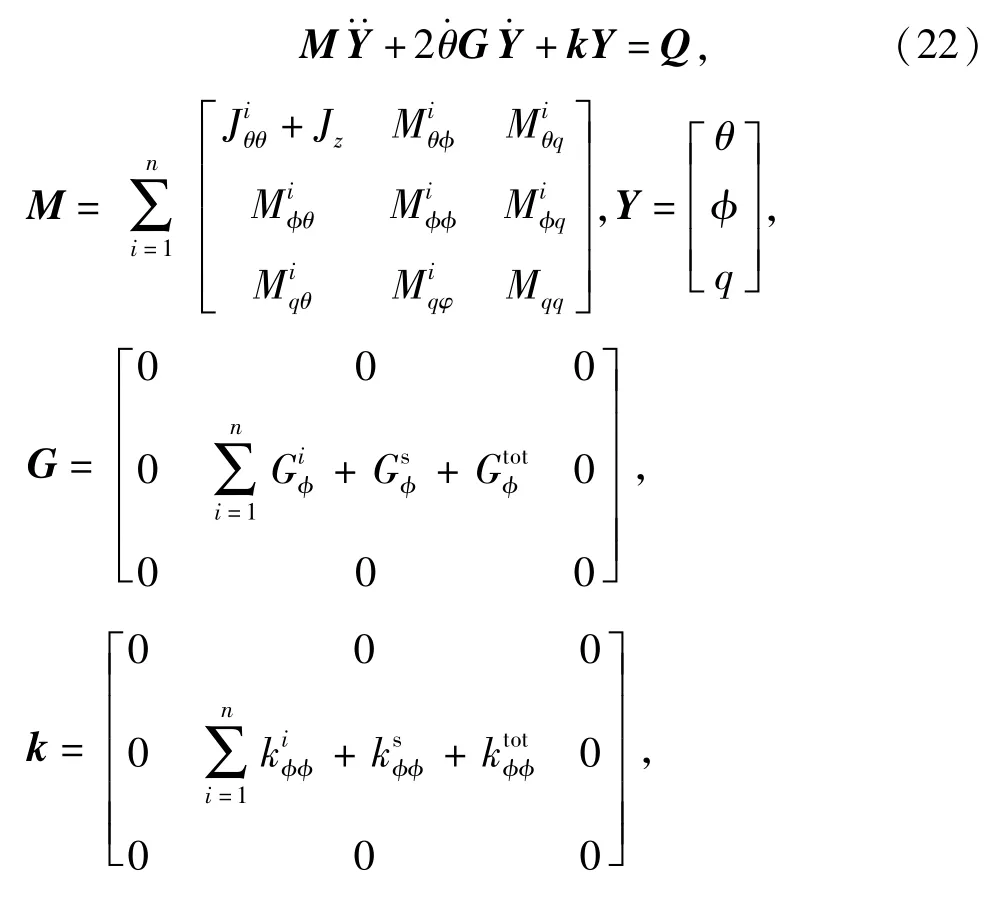
3 基于变胞原理的装填机构仿真误差分析

取柔性连杆的长度l=0.8 m，密度ρ=7.8× 103kg/m3，横截面积S=1.5×10-3m2，截面惯性矩I=1.125×10-7m4，弹性模量E=2×1011N/m2，装填机的旋转半径R=400 mm.炮弹是通过装填机输送到输弹线上，因此可以将装填机的末端位移作为衡量基于变胞原理的装填机构误差的主要参数。对刚性系统和刚-柔耦合后系统的杆末端位移进行仿真比较，得到仿真结果如图6和图7所示。杆的变形将引起装填运动末端位移的改变，对刚性系统和刚-柔耦合后系统装填机的末端位移进行仿真比较，得到仿真结果如图8和图9所示。

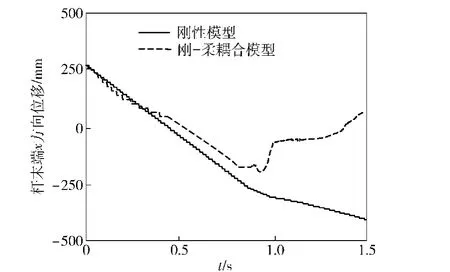
图6 杆的末端x方向位移Fig.6 End displacement of rod in x direction

从仿真结果可以看出，当考虑连接杆柔性时，装填机末端位移存在一定偏差，在直线轨道和圆弧轨道过渡处以及最后装填机运动停止时误差较大，并且局部出现振荡，这就严重影响了装填机构的精度，从而影响供弹精度。因此，为了提高装填机构的精度，应该尽可能提高连接杆材料的刚度，合理的设计装填机运行轨道。

图7 杆的末端y方向位移Fig.7 End displacement of rod in y direction

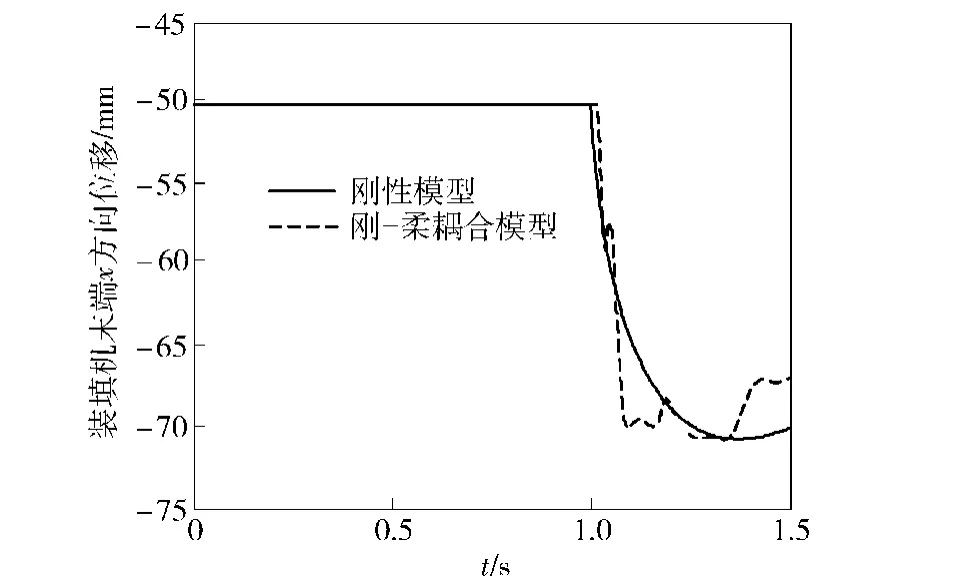
图8 装填机的末端x方向位移Fig.8 End displacement of loading machine in x direction

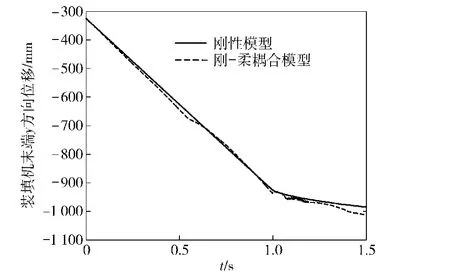
图9 装填机的末端y方向位移Fig.9 End displacement of loading machine in y direction

4 结论

传统的舰炮供弹系统结构复杂、精度低、兼容性差，这直接影响舰炮的供弹精度以及供弹速度，通过将变胞机构应用在舰炮供弹系统中，很好地解决了以往供弹系统的缺点，在舰炮供弹系统研究领域具有实际价值。应用刚-柔耦合动力学对其建模以及仿真分析，得到为了提高供弹系统的精度，应该尽可能提高连接杆材料的刚度，合理的设计装填机运行轨道，相比于传统所用的刚性假设，更具有理论上参考意义。此文只是对其进行仿真分析，如果想更真实地了解其存在的供弹精度问题，还需要进行样机制造以及试验研究。

（

）

［1］马献怀.155 mm舰炮装备技术发展探讨［J］.火炮发射与控制学报，2013（2）：99-102. MA Xian-huai.Technological development overview of 155 mm naval gun weapon system［J］.Journal of Gun Launch and Control，2013（2）：99-102.（in Chinese）

［2］Dai J S，Jones J R.Mobility in metamorphic mechanisms of foldable/erectable kinds［J］.Journal of Mechanical Design，1999，121（3）：375-382.

［3］王汝贵，戴建生.一种新型平面-空间多面体可重构变胞机构的设计与分析［J］.机械工程学报，2013，49（11）：29-35. WANG Ru-gui，DAI Jian-sheng.Design and analyses of a novel plane-space polyhedral reconfigurable metamorphic mechanism［J］.Journal of Mechanical Engineering，2013，49（11）：29-35.（in Chinese）

［4］张劲夫，许庆余，张凌.具有粘性摩擦的弹性曲柄滑块机构的动力学建模及计算［J］.西安交通大学学报，2000，34（11）：86-89. ZHANG Jin-fu，XU Qing-yu，ZHANG Ling.Dynamic modeling and calculation of slider-crank mechanism with elastic connecting rod and viscous friction［J］.Journal of Xi'an Jiaotong University，2000，34（11）：86-89.（in Chinese）

［5］陈思佳，章定国.带有载荷的柔性杆柔性铰机器人刚柔耦合动力学分析［J］.南京理工大学学报，2012，36（1）：182-188. CHEN Si-jia，ZHANG Ding-guo.Rigid-flexible coupling dynamics of flexible-link and flexible-joint robots carrying payload［J］.Journal of Nanjing University of Science and Technology，2012，36（1）：182-188.（in Chinese）

［6］蔡国平，洪嘉振.考虑附加质量的中心刚体-柔性悬臂梁系统的动力特性研究［J］.机械工程学报，2005，41（2）：33-40. CAI Guo-ping，HONG Jia-zhen.Dynamic study of hub-beam system with tip mass［J］.Journal of Mechanical Engineering，2005，41（2）：33-40.（in Chinese）

［7］Kane T R，Ryan R R，Banerjee A K.Dynamics of a cantilever beam attached to a moving base［J］.Journal of Guidance，Control and Dynamics，1987，10（2）：139-151.

［8］Sharf I.Geometric stiffening in multibody dynamics for-mulations［J］.Journal of Guidance，Control and Dynamics，1995，18（4）：882-890.

［9］刘铸永.刚-柔耦合动力学建模理论与仿真技术研究［D］.上海：上海交通大学，2008：21-68. LIU Zhu-yong.Study on modeling theory and simulation technique for rigid-flexible coupling systems dynamics［D］.Shanghai：Shanghai Jiao Tong University，2008：21-68.（in Chinese）

［10］古青波.中腹摆弹机构刚-柔耦合动力特性分析及其主动振动抑制［D］.哈尔滨工程大学，2013：41-57. GU Qing-bo.Rigid-flexible coupling dynamics analysis and active vibration suppression of the abdominal shell-swinging mechanism［D］.Harbin：Harbin Engineering University，2013：41-57.（in Chinese）

Rigid-flexible Coupling Dynamic Modeling and Error Analysis of Loading Mechanism of Naval Gun Based on Metamorphic Principle

HU Sheng-hai1，GUO Chun-yang1，YU Wei2，QI Song1，SUN Jun-chao1
（1.School of Mechanical and Electrical Engineering，Harbin Engineering University，Harbin 150001，Heilongjiang，China；2.Institute of Chemical Materials，China Academy of Engineering Physics，Mianyang 621900，Sichuan，China）

In order to meet the development needs of large caliber naval gun，a loading mechanism based on the metamorphic principle is proposed.The structure of loading mechanism is designed by using the metamorphic principle，and the motion description and principle analysis of the structure are conducted by combining the kinematic diagram of mechanism.The flexible rod is divided into some beam elements by using finite element discrete method，the deformation of beam elements is descripted under the mixed coordinate system，and a dynamic equation of the flexible rod is presented.A rigid-flexible dynamic equation is established by using Hamilton variational principle.The simulation result is gotten through the combined simulation of Adams and Ansys.The result shows that a big ammo-feeding error exists in the loading mechanism based on the metamorphic principle when the system moves in a large range at a highspeed.The influence of the flexible deformation of rod on loading accuracy should be considered in the research of large caliber naval gun based on the metamorphic principle.

ordnance science and technology；metamorphic principle；loading mechanism；rigid-flexible coupling；ammo-feeding error

TH12

A

1000-1093（2015）08-1398-07

10.3969/j.issn.1000-1093.2015.08.004

2014-12-04

国家自然科学基金项目（51175099）

胡胜海（1954—），男，教授，博士生导师。E-mail：hushenghai@hrbeu.edu.cn