改善单相混合励磁磁通切换电机转矩死区的不对称转子建模与测试

张宗盛 王秀和 杨玉波

（山东大学电气工程学院 济南 250061）

1 引言

磁通切换型磁阻电机（Flux Switching Motor,FSM）是在开关磁阻电机的基础上发展而来的一种新型双凸极电机[1]，除了具有开关磁阻电机的一系列优点外，还有更高的绕组利用率、更简单的控制电路等优点。按励磁方式不同，分为电励磁、永磁体励磁及混合励磁[2-5]。电励磁 FSM由励磁绕组提供励磁磁动势，通过调节励磁电流可以方便地调节励磁磁动势，但存在励磁电流较大、损耗较高的缺点；永磁式FSM利用永磁体提供励磁磁动势，不需要励磁电流但存在气隙磁场难以调节的问题[6,7]；混合励磁磁通切换电机（Hybrid Excitation Flux Switching Motor, HEFSM）由励磁电流与永磁体共同提供励磁磁动势，所需励磁电流较小且方便调节具有较高的研究价值。FSM 有多相及单相结构，多相FSM又以三相结构为主，通过其比较灵活的定转子极数比的设计，可以实现很好的三相电流对称性，研究多借助于交直轴数学模型等方法，分析及实验研究表明：通过一定的控制策略，三相FSM具有良好的转矩输出能力和恒功率弱磁扩速能力，在交流驱动领域具有良好的应用前景[8-13]。

单相FSM的定转子极数比恒为2:1，其结构较三相FSM更为简单，单相也就意味着所需的控制电路最为简单。尤其是采用混合励磁结构时，单相HEFSM 较三相 HEFSM 电机叠片造型简单易于装配。但是由于受结构影响单相FSM存在定转子极轴线重合位置，该位置下电机磁路磁阻达到极小值点，从而产生转矩死区[14-16]。有不同学者就单相 FSM转矩死区问题进行了一系列研究，归纳起来主要有两种方法：采用辅助装置与改善转子叠片的形状[17,18]。在定子或转子上安装辅助装置能够改善转子位于转矩死区位置时的电机起动性能，但却会削弱电机运行时的稳定性，同时额外的辅助装置会增加电机制造成本增大加工难度。改善转子叠片的形状主要有采用不对称气隙、转子叠片置孔等措施，其改善转矩死区效果并不是很理想，且转子叠片形状比较复杂，加工难度提高。

本文研究了一种不对称的转子结构，通过该转子可以削弱单相 HEFSM的转矩脉动，同时还分析了带有该转子结构的简化模型的建模方法；最后进行了有限元仿真分析与实验测试。结果表明，该转子结构能够有效地改善单相HEFSM转矩死区问题。

2 单相HEFSM工作原理与转矩死区

2.1 单相HEFSM工作原理

本文所研究的单相HEFSM如图1所示。

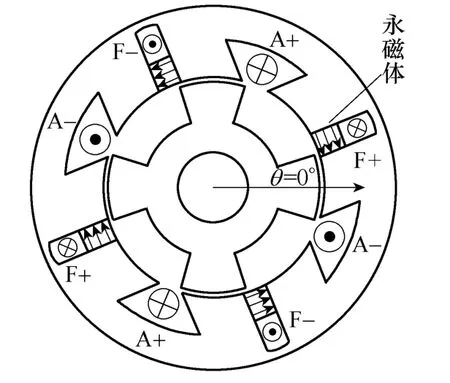
图1 单相HEFSM结构示意图Fig.1 Schematic diagram of single-phase HEFSM

线圈F1～F4串联组成励磁绕组F、线圈A1～A4串联组成电枢绕组A；永磁体与励磁绕组导体放置在同一定子槽内，永磁体沿切向充磁，励磁电流为直流。永磁体等效成一个恒定的虚拟内禀磁动势Fc与一个磁阻Rm的串联支路，励磁电流产生磁动势为Ff，在不同的转子位置，永磁体、励磁绕组作用于气隙的磁动势方向相同，两者并联组成励磁磁动势，如图2所示。

图2 混合励磁磁路示意图Fig.2 Hybrid excitation magnetic circuit

励磁电流方向不变，则等效励磁磁动势Fef方向不变。通以电枢电流后，励磁、电枢磁动势的合成磁动势位于其中导体电流相反的励磁绕组槽与电枢绕组槽之间定子极轴线上，电枢电流方向随转子位置不同而转换，电枢电流的每次换向都会使定子合成磁动势在空间上切换 45°，令电机转子在直流磁场和交流磁场的共同作用下产生旋转运动。

2.2 单相HEFSM转矩死区分析

单相电励磁FSM有励磁、电枢绕组的串联与并联两种控制方式，而对于 HEFSM不宜采用串联控制，因为不能实现对励磁电流的单独调节功能，所以本文中对 HEFSM采用并联控制方式。作为磁阻类电机，可采用APC（angular position control）、CCC（current chopping control）两种控制策略，本文采用导通区间为45°的CCC控制策略，该策略有利于调节励磁电流的大小，同时最大程度上避免绕组电流关断带来的转矩死区。基于此策略，利用Ansoft Simplorer V10与 Ansoft Maxwell 14 2D搭建了HEFSM系统的联合仿真模型，其中HEFSM为图1所示的常规转子结构，图3为不同电流斩波之下的转矩仿真结果曲线簇。

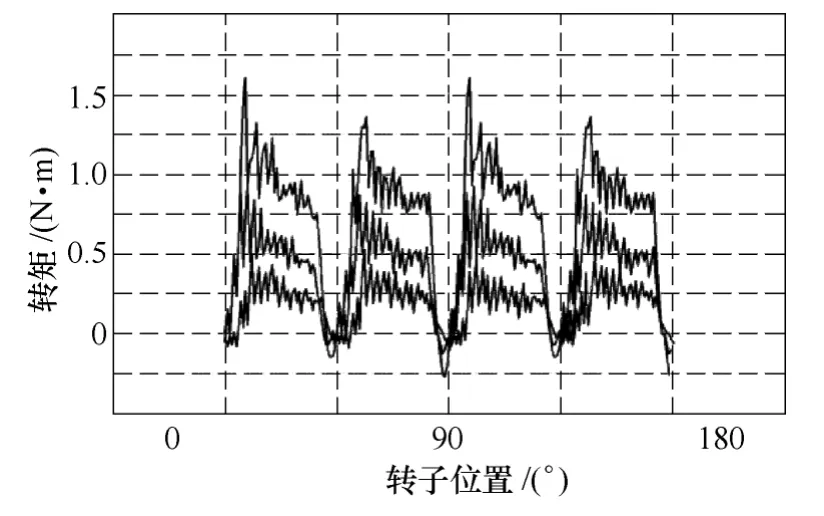
图3 常规转子转矩仿真曲线Fig.3 Simulation torque curves of the conventional rotor

从图 3中可以看出每条转矩曲线均存在过零点，转矩过零点也就是在定转子极轴线重合的位置，即使能够理想地进行电枢电流的换向，该位置下电机的电磁转矩为零。并且在电机运行时存在摩擦阻力等因素，所以单相HEFSM存在转矩死区。

3 不对称转子结构设计与建模

3.1 不对称转子结构设计

从本质上看 HEFSM的运行原理遵循“磁阻最小原理”，即磁通总要沿着磁阻最小的路径闭合，而具有一定形状的铁心在移动到最小磁阻位置时，必使自己的主轴线与磁场的轴线重合。HEFSM 转子的主轴线为转子极轴线，磁场的轴线沿励磁、电枢合成磁动势的方向即定子极的轴线。当HEFSM为8/4极结构时，存在图1所示的转子极轴线与定子极轴线重合位置，该位置即为转矩死区的中心点。

HEFSM的转子结构比定子简单，本文同样从设计转子结构入手来解决转矩死区问题。本文所研究的不对称转子结构分为叠片数量相等的 a、b两部分，这两部分的极弧长度不等，如图4a、4b所示，这两部分沿轴向装配时如图 4c所示，所以该转子结构沿径向为非对称结构。

图4 不对称转子结构Fig.4 Asymmetric rotor structure

通过前文可知，转子的a、b两部分均会产生转矩死区，其死区的中心位置如图4a、4b所示，当两者不对称装配后，其转矩死区中心位置不会重叠，a、b两部分叠片轴线的夹角Δθ越大越是有利于避免两者的转矩死区的重合。电枢电流的换向区间依然为45°，根据上述 a、b极弧长度的选取，转子在 45°区间内，a、b极轴线不可能与定子极的轴线同时重合，通过恰当的控制电枢电流换向时刻，可达到改善转矩死区目的。

若定义τs为定子极弧长度，τslot为槽口宽度。为尽可能的增大Δθ的数值转子 a、b两部分的极弧长度分别取为

本文所设计装配有不对称转子的 HEFSM样机主要尺寸参数见下表。

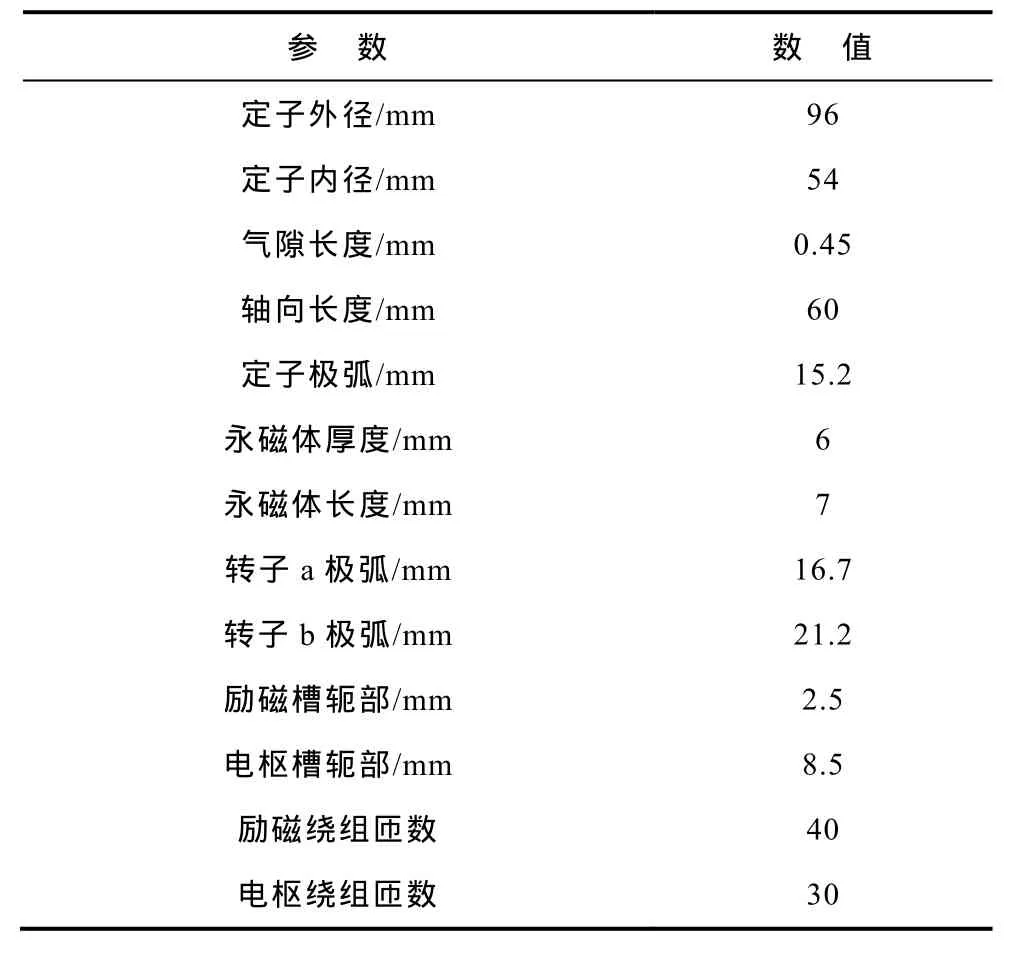
表 HEFSM样机的主要尺寸参数Tab. The parameters of prototype HEFSM

3.2 带有不对称转子的HEFSM简化模型

由于转子结构的不对称，定转子间的气隙形状更为复杂，建立电机的准确模型不易实现，因此本文建立了 HEFSM 的简化模型。在电机结构上 HEFSM的励磁绕组槽轭部截面积很小，从图2所示磁路可以看出，励磁电流逐渐增大，该部分的磁通密度会逐渐减小至零后又逐渐增大，所以该部分的磁导变化范围受励磁电流的影响很大。其余铁心部分磁通密度不会过高且变化范围较小可忽略其磁导。单相HEFSM的简化磁路模型如图 5所示。图中，Gy为励磁绕组槽轭部磁导；Ff为励磁绕组磁动势；Fa为电枢绕组磁动势；每对定子极可区分为 s1、s2两个极，分别为励磁槽逆时针侧与顺时针侧，s1、s2与邻近转子极间的气隙磁导分别表示为Go1、Go2。

图5 单相HEFSM的简化磁路模型Fig.5 Simplified circuit model of single-phase HEFSM

根据磁路结构的对称性，以结点0为磁动势参考点，电枢绕组磁通为φa，则有结点磁路方程为

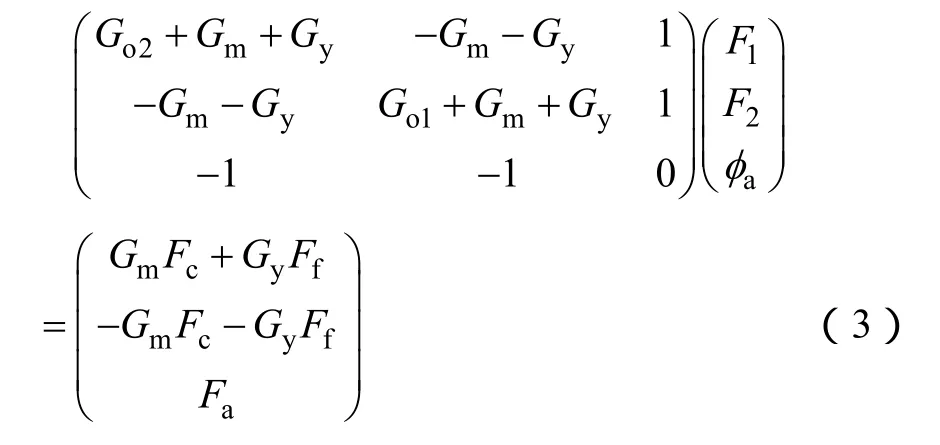
通过迭代方法求解结点磁路方程，得F1、F2和φa，进而可得式（4）、式（5）；励磁、电枢绕组均为4线圈串联而成所以可得式（6）～式（8）。

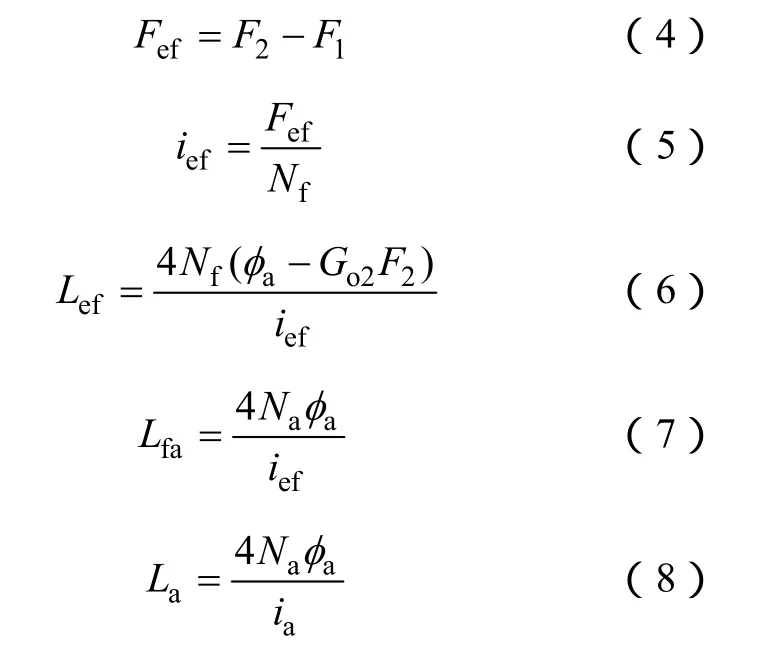
式中，ief、Lef为等效的励磁绕组电流、自感；La为电枢绕组自感；Lfa为互感。

利用式（4）～式（8）可得电机电磁转矩Te为

3.3 气隙磁导的求解

不对称转子结构改变了 HEFSM磁通密度分布沿轴向均匀分布的特点，借助于 3D电磁场有限元仿真软件可以对该类转子进行仿真耗时耗力，对分析 HEFSM带来不便，若建立简洁的数学模型则会极大的提高其实用价值。

图5中的Go1、Go2可认为分别包含两部分且是以转子位置角θ为变量的函数，故可表示为

式中，Ga1(θ)、Ga2(θ)为转子 a 部分与定子极 s1、s2间的气隙磁导；Gb1(θ)、Gb2(θ)为转子b部分与定子极s1、s2间的气隙磁导。

相同定转子极弧长度的 8/4极单相 HEFSM与8/4极的单相开关磁阻电机（SRM）在定转子极间气隙结构上是一致的。而单相 SRM 不存在绕组耦合的问题，所以利用单相 SRM 电感有限元仿真结果及电感与回路磁导间的关系可快速的确定某一定子极与转子极之间的气隙磁导，在忽略铁心磁导的基础上，电感与气隙磁导的关系为[19]

若以图 3a、3b所示为转子位置角参考零点，Ga1(θ)、Gb1(θ)用上述方法确定的曲线如图6所示。

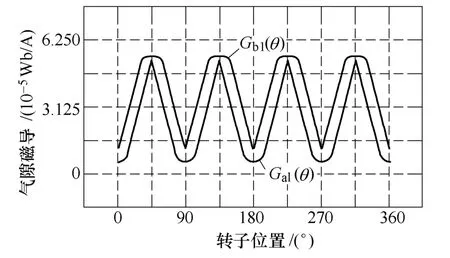
图6 气隙磁导有限元仿真曲线Fig.6 Air gap permeance curve of finite element analysis

若定义a部分轴线与定子轴线重合的位置为参考零点，利用傅里叶级数拟合可获得Ga1(θ)、Gb1(θ)的表达式。由其曲线可知为偶函数，所以只用傅里叶级数中的余弦分量拟合为

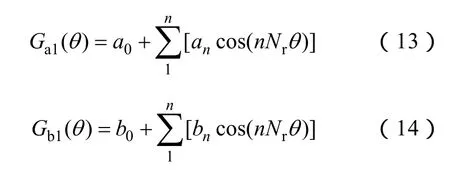
因此 s2与定子极间气隙磁导Ga2(θ)、Gb2(θ)为

根据图 3c中转子的装配方式，a、b两部分轴线的夹角为

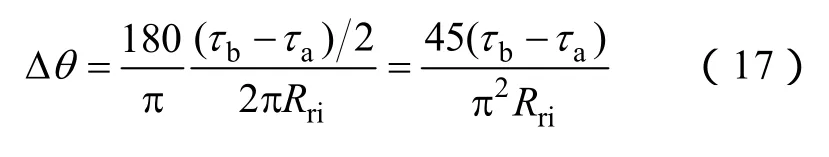
所以有

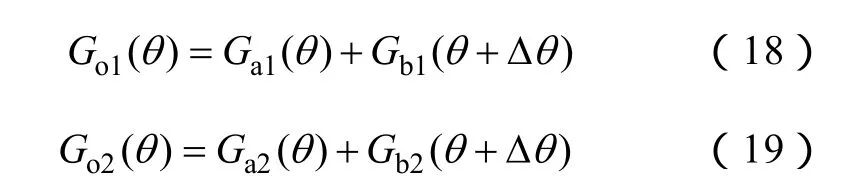
至此便可求得式（10）、式（11）气隙磁导的数学表达式，代入式（3）后，最终将能够给实现式（9）的求解，实现对电机转矩的求解。

4 仿真与测试分析

4.1 有限元仿真分析

装有不对称转子的 HEFSM的换向时刻应在转子a、b两部分轴线夹角的某条角分线与定子极轴线的重合时刻。通过表1数据可求得式（13）所示的Δθ约为12°，也就是说若以转子a部分轴线与定子轴线重合的位置为参考点，则不对称转子 HEFSM的电枢电流换向时刻可较对称转子提前0～12°。在进行有限元仿真时设定为提前 10°。图 7为给定励磁电流if=3A、电枢电流ia=|4|A条件下，利用本文提出的数学模型计算与 3D有限元分析得到的不同转子位置电磁转矩结果。从图中可以看出，在该激励电流下不同转子位置角均可产生电磁转矩，存在改善转矩死区的效果。

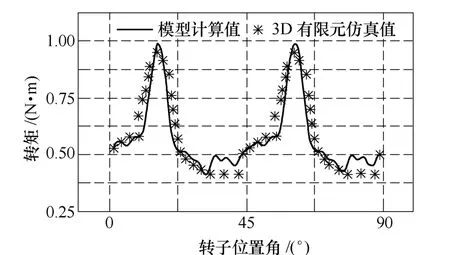
图7 给定电流下电磁转矩分析结果对比Fig.7 Torque value comparison between the model calculation and the 3D finite element analysis

4.2 联合仿真分析

为考察控制电路对转矩输出的影响，利用Ansoft Simplorer V10搭建了并联控制仿真外电路，与利用Ansoft Maxwell 14 3D搭建的电机本体仿真模型构成了联合仿真模型。通过设置仿真电路中的开关器件等仿真元件参数，能够很好地模拟实际元件的特性，所以仿真电路会表现出受到开关器件延时等因素的影响，因此将以超前转子a部分轴线与定子轴线重合位置 12°的位置为分析不对称转子HEFSM的参考零点。

直流电源电压为80V；因励磁电流的方向不变所以采用电流滞环斩波控制，滞环宽度为0.2A；而电枢电流要随转子位置而换向，为提高其响应速度未进行滞环设置；仿真步长为1×10-4s。图8为控制if=3A、ia=4A，转速为750r/min时的联合仿真结果。

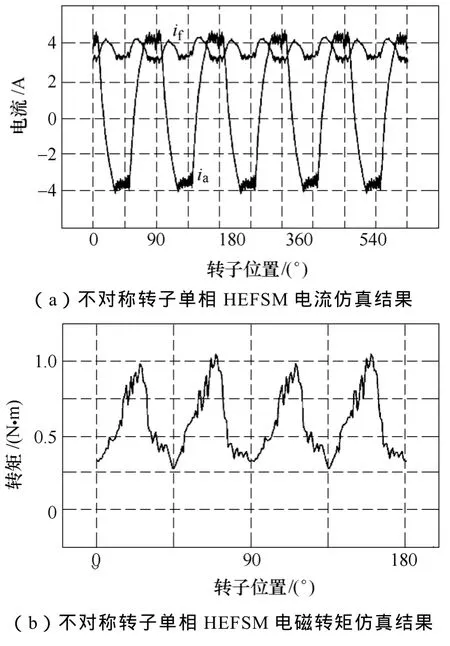
图8 联合仿真结果曲线Fig.8 The results of combined simulation model

由图8b与图7的对比可以，在外电路的控制电机连续运行过程中，转矩的最低点约为0.25N·m较图7中的转矩最小值有所降低，但与图3所示的常规转子HEFSM的转矩曲线相比消除了转矩过零点，说明在电机运行过程中改善转矩死区效果明显。

4.3 感应电动势测试分析

考虑到实验的可行性，进行了电枢绕组的感应电动势的测试，电机给定转速为 1 000r/min，励磁电流为零，即测试永磁体对电枢绕组的影响。图 9为电枢绕组感应电动势的简化模型计算值与实验测试波形，其中，图9a中参考零点与联合仿真模型中一致，从两者的对比可以看出，本文提出的简化模型的准确度比较高。从图9可以推出不对称转子结构并没有明显改变电机互感导数极性不变的区间范围，说明电机的出力与绕组的互感、自感均有关系，这改变了常规转子 FSM 绕组自感总体上不输出功率的情况，有利于改善电机转矩死区。

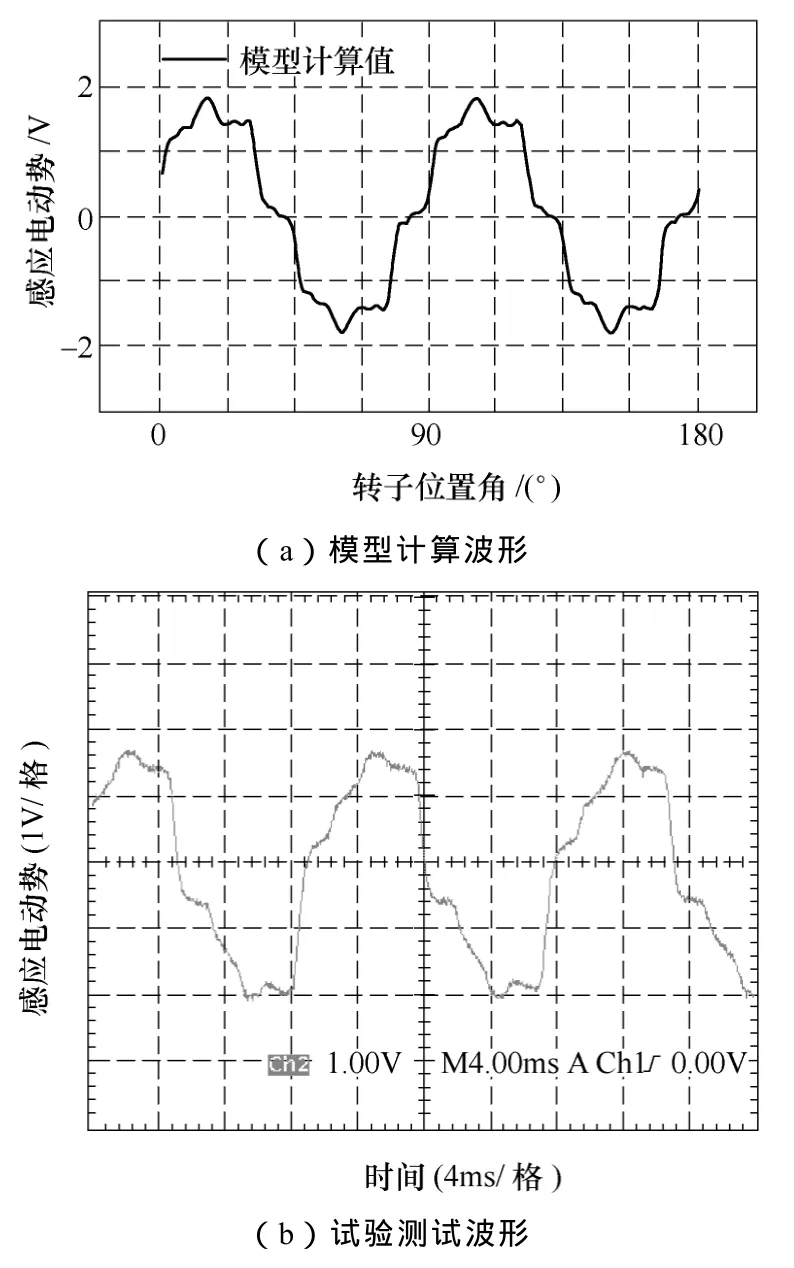
图9 电枢绕组感应电动势波形Fig.9 The EMF waveforms of armature winding

4.4 转矩测试分析

转矩测试平台的组成如图 10所示。动态转矩传感器采用 Lonrenz Messtechnik GmbH的产品 DR-3000，最大偏差为 50mN·m，采样频率为 2 500次/s[20]。通过磁滞测功机为电机施加负载，HEFSM采用并联控制外电路，控制电路设置与联合模型中的仿真电路设置一致。

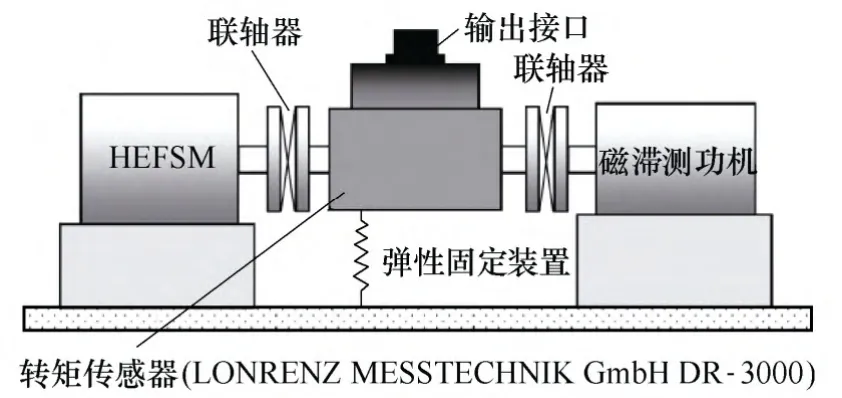
图10 转矩测试平台示意图Fig.10 Schematic diagram of torque test platform

测试时给定负载0.5N·m，考虑到起动时刻的摩擦阻力较大等因素，在起动时的电流控制值较大为if=ia=5A。转矩波形的初始位置即为过零点。图11为实验测试结果，从图11可以看出，电流实验波形与仿真波形基本一致，而转矩实验波形与图8b的转矩仿真波形差别较大，实验波形甚至出现了负值，其主要原因在于：转矩的仿真波形为电机本身的理论上的转矩输出，不受负载的影响。转矩传感器测量的是两个轴端的转矩差值，受电机与负载之间作用力的影响。

图11 实验测试结果Fig.11 Experimental test waveforms

负载设置为0.5N·m恒定值，由图8b可知即使在一个转子步距内电机的电磁转矩也存在大于或小于负载转矩的不同情况，这使得电机即使在稳定运行时也是始终处于不断的加、减速状态，转速非恒定值而是在一定范围内波动。电机的转动惯量要明显小于负载的转动惯量，电机、负载之间的相互作用力变得更为复杂。在电机转速下降时，负载减速反应较电机有一定的滞后，此时转矩传感器测量值较实际值偏小，同理电机转速上升时测量值较实际值偏大，因此转矩的实验波形较电磁转矩仿真分析波形得波动更为严重，乃至出现反向转矩值。电机在起动的瞬间电机为加速状态负载更接近理想状态，所以初始波形较为理想。

如在图11b中，S点为电枢电流关断并开始换向的时刻，t1区域内的波形出现负值明显与理论曲线差异很大，出现较大的反向转矩波形尖峰，而图11a中的电流波形并不存在突变，所以出现很大的反向转矩是明显有悖于能量守恒的，其成因是该区域内出现大转动惯量的负载带动小转动惯量的电机正向旋转的情况，以至传感器两个连接轴之间的转矩差值即变为负值。当电枢电流换向完毕，逐渐转换为电机拖动负载旋转的状态，在此过程中出现t2区域所示的转矩曲线抖动情况。电机拖动负载逐渐的稳定的过程中，电机与负载之间的相互作用力逐渐变的更为复杂：时而电机拖动负载旋转，时而因转动惯量的原因使得负载带动电机旋转，从而转矩传感器的输出波形表现为上下波动，与理论波形的差异十分明显。

从前文分析可知，在电枢电流换向的转子位置点转矩输出能力最弱，因此对该转子位置进行转矩测试，看电机能否起动可验证不同转子结构的改善转矩死区的效果，如图12所示。不对称转子结构使得电机在电枢电流换向位置点能够在轻微抖动后起动，说明在该位置不存在转矩死区，而对称转子结构则在抖动后转矩归零出现转矩死区，无法起动。

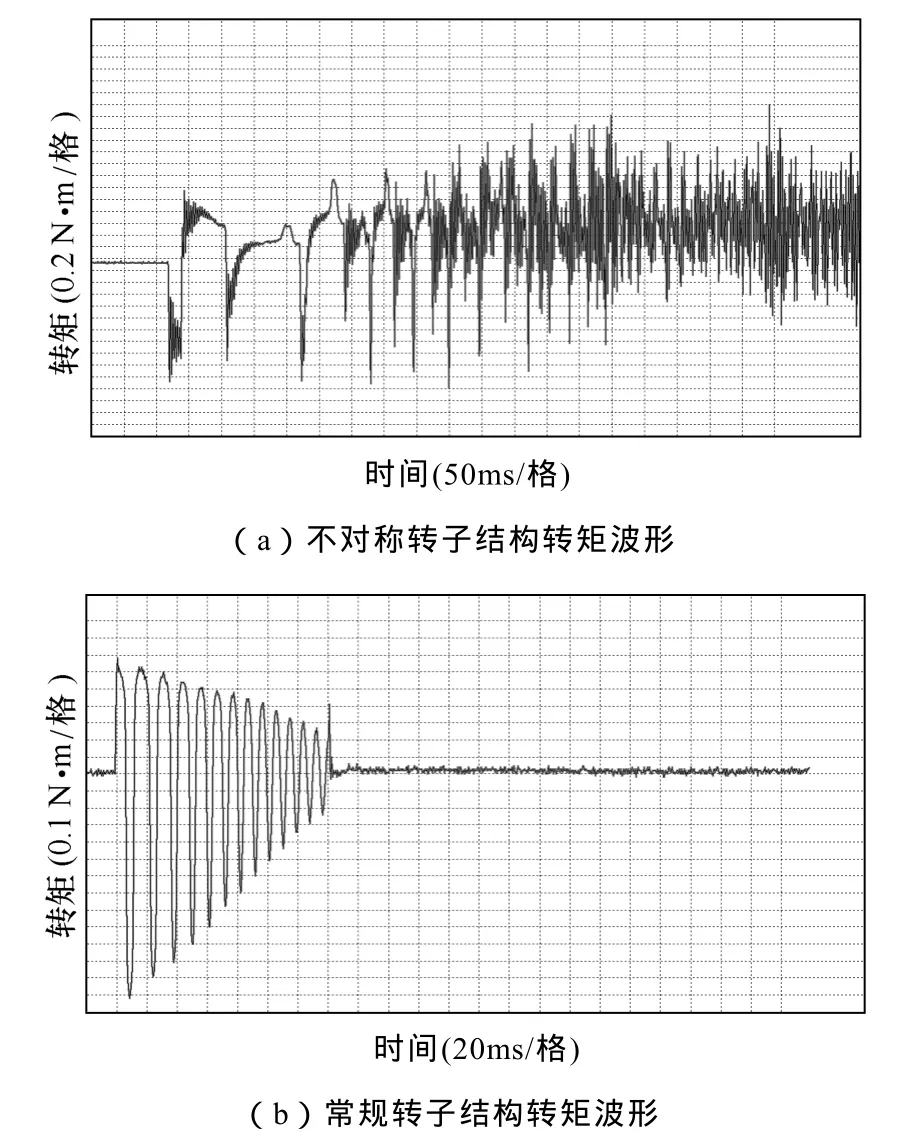
图12 不同转子结构的电枢电流换向点转矩波形Fig.12 Torque test waveforms of different rotor structures at armature current reversal position

5 结论

本文研究了一种适用于改善单相 HEFSM转矩死区的不对称转子结构，通过介绍该转子的结构特点说明了其改善单相 HEFSM转矩死区的原理，同时还介绍了一种针对该转子的简化模型的建模方法，最后进行了有限元仿真与联合仿真分析与实验测试，分析了实测结果与理论上差异的成因，并进行了特殊转子位置的实验对比，其结果表明本文所研究的不对称转子结构可有效的改善单相 HEFSM的转矩死区问题，所建简化模型的准确性也较高。

[1] Pollock C, Wallace M. The flux switching motor, a DC motor without magnets or brushes[C]. Proceedings of 34th Annual Meeting of the IEEE Industry Applications, Phoenix, 1999, 3: 1980-1987.

[2] Hoang E, Ahmed A H Ben, Lucidaume J. Switching flux permanent magnet polyphased machines[C].Proceeding of European Conference of Power Electronic and Applications Trondheim, Norway, 1997(3): 903-908.

[3] Zhu Z Q, Pang Y, Howe D, et al. Analysis of electromagnetic performance of flux-switching permanent magnet machines by nonlinear adaptive lumped permanent magnet circuit it model[J]. IEEE Transactions on Magnetics, 2005, 41(11): 4277-4287.

[4] Hoang E. Flux-switching dual-excitation electrical machine: EP, 20070726708[P]. 2008-12-17.

[5] 花为, 程明, 诸自强, 等. 新型两相磁通切换型双凸极永磁电机的静态特性研究[J]. 电工技术学报,2006, 21(6): 70-77.

Hua Wei, Cheng Ming, Zhu Z Q, et al. Study on static characteristics of a novel two-phase flux-switching doubly-salient permanent magnet machine[J]. Transactions of China Electrotechnical Society, 2006, 21(6):70-77.

[6] Chai K S, Pollock C. Using genetic algorithms in design optimization of the flux switching motor[C].Conference of Power Electronics, Machines and Drives,2002: 540-545.

[7] Chen Y, Chen S, Zhu Z Q, et al. Starting torque of single-phase flux-switching permanent magnet motors[J]. IEEE Transactions on Magnetics, 2006, 42(10):3416-3418.

[8] 花为, 程明. 新型三相磁通切换型双凸极永磁电机电感特性分析[J]. 电工技术学报, 2007, 22(11):21-28.

Hua Wei, Cheng Ming. Inductance characteristics of 3-phase flux-switching permanent magnet machine with doubly-salient structure[J]. Transactions of China Electrotechnical Society, 2007, 21(11): 21-28.

[9] Owen R L, Zhu Z Q, Jewell G W. Hybrid excited flux-switching permanent-magnet machines with iron flux bridges[J]. IEEE Transactions on Magnetics,2010, 46(6): 1726-1729.

[10] 许泽刚, 谢少军, 毛鹏. 混合励磁磁通切换电机等效磁路模型[J]. 中国电机工程学报, 2011, 31(30):124-131.

Xu Zegang, Xie Shaojun, Mao Peng. Equivalent magnetic circuit model of flux-switching hybrid excitation machine[J]. Proceedings of the CSEE, 2011,31(30): 124-131.

[11] 王宇, 邓智泉, 王晓琳. 基于空间矢量调制的电励磁磁通切换电机转矩角增量控制[J]. 中国电机工程学报, 2012, 32(3): 75-82.

Wang Yu, Deng Zhiquan, Wang Xiaolin. A torque angel increment control strategy for electrical excitation flux-switching machines based on space vector modulation[J]. Proceedings of the CSEE, 2012, 32(3): 75-82.

[12] 贾红云, 程明, 花为, 等. 基于死区补偿的磁通切换永磁电机定子磁场定向控制[J]. 电工技术学报,2010, 25(11): 48-55.

Jia Hongyun, Cheng Ming, Hua Wei, et al. Statorflux-oriented control for flux-switching permanent magnet motor based on dead-time compensation[J].Transactions of China Electrotechnical Society, 2010,25(11): 48-55.

[13] 刘细平, 左亮平, 刁艳美, 等. 轴向磁通切换混合励磁电机励磁控制系统[J]. 电工技术学报, 2013,28(10): 97-102.

Liu Xiping, Zuo Liangping, Diao Yanmei, et al.Excitation control system of axial flux-switching hybrid excited machine[J]. Transactions of China Electrotechnical Society, 2013, 28(10): 97-102.

[14] Bangura J F. Design of high-power density and relatively high efficiency flux-switching motor[J]. IEEE Transactions on Energy Conversion, 2006, 21(2): 416-425.

[15] 张宗盛, 王秀和, 杨玉波. 新型混合励磁磁通切换型磁阻电机的变结构磁路模型[J]. 中国电机工程学报, 2014, 34(21): 3467-3474.

Zhang Zongsheng, Wang Xiuhe, Yang Yubo. A variable structure magnetic circuit model of novel hybrid excitation flux switching motors[J]. Proceedings of the CSEE, 2014, 34(21): 3467-3474.

[16] 张宗盛, 王秀和, 杨玉波, 等. 单相磁通切换型磁阻电机的快速建模方法[J]. 电机与控制学报, 2014,18(7): 6-11.

Zhang Zongsheng, Wang Xiuhe, Yang Yubo, et al.Speedy Modeling method for single-phase flux switching motor[J]. Electric Machines and Control, 2014,18(7): 6-11.

[17] 吴建华. 开关磁阻电机设计与应用[M]. 北京: 机械工业出版社, 2000.

[18] Chen Y, Chen S, Zhu Z Q, et al. Starting torque of single-phase flux-switching permanent magnet motors[J]. IEEE Transactions on Magnetics, 2006, 42(10):3416-3418.

[19] 王秀和. 电机学[M]. 北京: 机械工业出版社, 2009.

[20] Lorenz Messtechnik Gmbh. Operation manual for configuration and evaluation software DR-USB-VS[EB/OL]. www.lorenz-sensors.com.