现代高性能永磁交流伺服系统综述——传感装置与技术篇

莫会成 闵 琳

（西安微电机研究所 西安 710077）

1 概述

一般而言，伺服系统是指利用负反馈原理通过各种控制方法或策略，使输出服从于输入的运动控制系统。伺服系统的组成如图1所示。它的主要任务是按控制命令的要求使输出能够自动地、连续地、精确地、快速地复现输入信号地变化规律。通过机械位移、机械角度、转矩、速度或加速度等输出量达到各种各样的控制目的。永磁交流伺服系统是一种用永磁交流伺服电动机作为执行电机，以伺服电机的速度、机械位置或角度作为控制对象的运动控制系统，由此可知伺服系统主要由电机、传感器与驱动控制器三大主要部分组成。

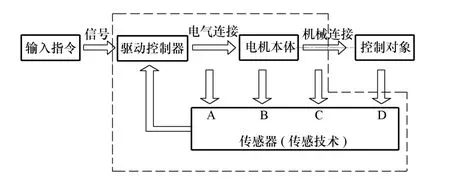
图1 伺服系统构成框图（虚线内是核心构成部分）Fig.1 Structure of servo system

传感器是能感受被测量并按照一定的规律转换成可用信号的器件或装置，通常由敏感元件和转换元件组成[1]，用于满足系统信息传输、存储、显示、记录或控制等要求。伺服系统的传感器必须能够准确地测量出反映伺服系统工作的各个物理量，并且迅速地传递给控制器。传感器的水平在一定程度上决定了系统的水平，有时甚至成为影响系统工作的关键。因此，伺服系统中传感装置与技术的作用非常重要。如果把驱动控制器比做人的大脑，电动机本体为人的四肢，那么传感器则是人的眼耳等各种感知器官，只有感知器官的精确定位，才可能使人通过大脑指挥四肢准确地完成各种动作。因此，传感器的性能好坏也直接影响着伺服系统的整体性能。

永磁交流伺服系统中使用的传感器和传感技术就是将与执行电机或控制对象相关的电流、速度、位置、加速度、温度等各种旋转的或直线的机械、电气等输出量反馈给驱动控制器，使之与输入的命令进行比较，驱动控制器根据这些信息做出决定，发布指令，指示执行电机完成相应动作。

永磁交流伺服系统中所使用的传感器和传感技术种类繁多，内容十分丰富，根据伺服驱动控制的工作原理，从图1的系统框图中可以看到，伺服系统大致接收处理四类信息：

第一部分A：是指能从电动机输入端所能直接或间接得到的信息，如电机的电压u、电流i、电压变化率 du/(dt)、电流变化率 di/(dt)、电机的反电动势e和电机磁链ψ等一些重要的电气参数。

第二部分B：是从电机本体可获得的有关参量，如电机的温度或温升、机械振动、噪声等各种环境监测物理量。

第三部分 C：主要输出的是电机各种机械物理量，如机械角度、电气角度、角速度、角加速度、直线位置和速度以及电机的磁场位置等。

第四部分D：主要是反馈被控对象的各物理量，除了直接的机械量如位置、速度、角度等以外，还有许多根据被控对象的性质而提供给上位控制器的各种监测控制参数。

要想全面的总结归纳上述所涉及到的各种类型物理量的传感器及传感技术是很困难的，也并非完全必要，本文将重点描述上述第三部分的机械量传感器和传感技术，而对除温度传感器外的其他各物理量的检测和传感则不作具体介绍。

2 传感器的主要种类、原理及特点

传感器的分类方法很多，根据伺服系统的工作状态可以分为位移传感器、速度传感器、加速度传感器、电流传感器等；按信号转换的原理可分为电磁感应原理、光电效应、光栅效应、霍尔效应、磁阻效应、压阻效应、压电效应等；按输出电信号的形式可分为模拟式和数字式。伺服系统中主要使用的传感器有旋转变压器、自整角机、测速发电机、光电编码器、磁性编码器、霍尔元件以及过压、过流、过热等非机械量测量传感器等。

以下简单介绍几种主要传感器的原理、结构及特点。

2.1 旋转变压器

旋转变压器是一种精密的电磁感应元件，当它的励磁绕组通电励磁后，其输出电压的幅值与转子转角成正弦或余弦函数关系，或在一定的转角范围内与转子的转角成正比[2]。在少数特殊的使用场合，通过绕组的特殊设计也可输出某些特殊函数，如正割函数、倒数、对数等。除旋转式外，还有直线式，即输出信号与直线位移成某种函数关系，如数控机床中常用它作位置检测。

旋转变压器的类型很多，按用途可分为解算用旋转变压器和数据传输用旋转变压器；按有无电刷和集电环之间的滑动接触可分为有接触式旋转变压器和无接触式旋转变压器（又称无刷旋变）；按极对数可分为单对极与多极和双通道旋转变压器等[3]。

从20世纪60年代起，旋转变压器逐渐用于伺服系统，80年代后随着现代伺服技术的发展，旋转变压器在通过R/D数字转换器进行模数转换后，大量应用于有定位要求的高性能位置伺服系统中作精密传感元件。如高档数控机床伺服系统、精密机器人伺服机构、新能源汽车电驱动系统及高性能武器装备伺服系统等等。特别是在一些环境恶劣的使用场合如强冲击、振动及极限高低温时，旋转变压器将替代光电编码器成为伺服系统反馈元件的不二选择。

现代位置伺服系统中常用的旋转变压器主要有单对极无接触正余弦旋转变压器、磁阻式多极旋转变压器、旋转或直线可变差动变压器（RVDT、LVDT）等几类，简要介绍如下：

2.1.1正余弦旋转变压器

旋转变压器实质上是原方绕组与副方绕组之间的电磁耦合程度可以随转子转角而变化的变压器。正余弦旋转变压器的副方绕组输出电压与转子转角成正弦或余弦函数关系。

普通的正余弦旋转变压器转子上的输出信号是利用电刷与滑环结构引出的，而现代永磁交流伺服电机系统使用的正余弦旋转变压器是具有高可靠性的无刷旋转变压器，以环形变压器代替电刷与滑环实现转子输出绕组与外电路的连接，消除了电刷与滑环间的滑动摩擦带来的接触不良等可靠性隐患。典型产品如图2所示。

图2 伺服系统用无刷旋转变压器Fig.2 Brushless resolver for servo system

对伺服系统来说，旋转变压器的精度是其最关注的指标。通常所说的旋转变压器的精度是指其电气误差指标，它反映的是旋转变压器的综合精度，直接影响到伺服系统的反馈精度。目前永磁交流伺服电机系统中使用的无刷旋转变压器精度通常要求小于 10′。在某些精密位置伺服系统中应用的多极高精度旋转变压器的精度可达到角秒级。

2.1.2磁阻式旋转变压器

磁阻式旋转变压器是一种基于磁阻变化原理的角位传感元件，实质上是磁阻可变的无接触式耦合变压器，其输出电压的幅值与转子转角呈正余弦函数关系。

磁阻旋变的结构同一般磁阻式电机结构形式相似，定子铁心为大齿，输入、输出绕组均为集中绕组并嵌放在定子铁心的大槽内，高精度的多极磁阻旋变定子大齿上还有均匀分布的小齿；转子铁心上不带绕组，仅为均匀分布的凸极或小齿，其凸极数或小齿数即是磁阻旋变的极对数。

一般情况下，永磁交流伺服系统中使用的磁阻旋变多与电动机的极对数相匹配，普通伺服系统使用的磁阻旋变极对数大多在2～6之间，定子大齿上无小齿，转子也仅是与极对数相等的凸极。这类磁阻旋变的精度按极对数的不同一般为 60′或 30′。典型产品如图3所示。

图3 普通伺服系统用磁阻式旋转变压器Fig.3 Variable reluctance resolver for servo system

从图3可以看出，普通永磁交流伺服系统中使用的磁阻旋变结构非常简单，其制造工艺特别适合大批量低成本生产。同时，由于没有电刷滑环接触，即可以提高精度，又具有工作可靠，抗冲击振动能力强，适应恶劣环境，并能连续高速长寿命运行的优点。近几年来，磁阻旋变以其独特的优势在汽车行业得到大量应用。

磁阻旋变的精度随着极对数的增加而提高，因而在高精度伺服系统中采用的磁阻旋变极对数较多，定子大齿上有均匀分布的小齿，转子相应也为多齿结构，带小齿的高精度磁阻旋变的冲片如图 4所示。

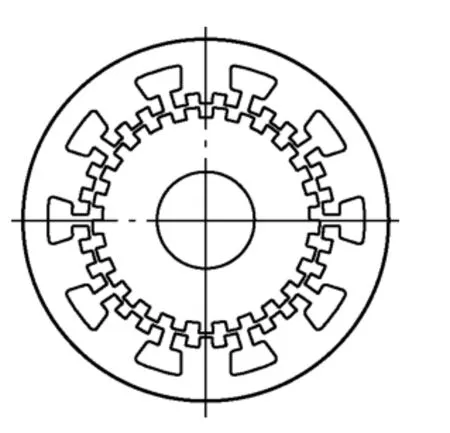
图4 高精度磁阻式旋转变压器冲片图Fig.4 Lamination of high-precise variable reluctance resolver

这类高精度的磁阻旋变的精度可达角秒级，如应用于某武器装备中的110机座180对极的磁阻旋变的精度高达3.5角秒。

2.1.3RVDT与LVDT

（1）RVDT。RVDT（Rotary Variable Differential Transformer）是旋转可变差动变压器的缩写，是一种磁阻式的线性旋转变压器，通过改变磁路气隙截面而改变磁路的磁导，并按差动变压器原理工作。

RVDT的输出电压幅值与转子转角成正比关系，是一种体积小、结构可靠、分辨率高、工作寿命长的无接触式角度检测元件。典型产品如图5所示。

图5 RVDT角位传感器Fig.5 Rotary variable differential transformer

（2）LVDT。LVDT（Linear Variable Differential Transformer）是直线可变差动变压器的缩写，又叫螺管型线性差动变压器，是一种直线位移传感元件。

LVDT由一次线圈（初级）、二次线圈（次级）以及铁心三部分组成。通过初级与次级的电磁耦合，使得铁心的位移变化量与输出电压变化量呈线性关系。LVDT的结构如图6所示。

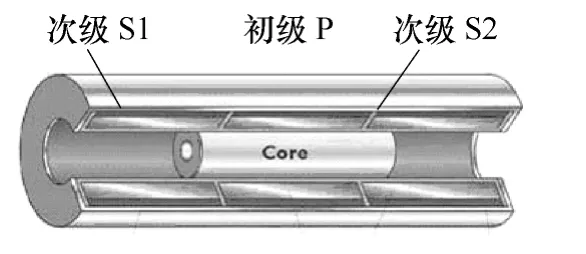
图6 LVDT结构图Fig.6 LVDT structure

LVDT工作过程中，铁心的运动不能超出线圈的线性范围，否则将产生非线性值，因此所有的LVDT均有一个线性范围。高线性度的LVDT的线性度可达0.1%，大量程的LVDT测量范围已有1m以上的规格。LVDT可以对铁芯最微小的运动做出响应并生成输出，外部电子设备的可读性是对分辨率的唯一限制，因而从理论上讲它具有无限的分辨率，实际产品分辨率一般可达 0.1μm。典型产品如图7所示。

图7 LVDT角位传感器Fig.7 Linear variable differential transformer

在现代永磁交流伺服系统中，无论使用哪种旋转变压器，都需要进行R/D变换，即可使用R/D变换专用芯片，也可将其功能以软件的形式集成在电机的驱动控制芯片（DSP）中，具体变换原理本文不再介绍。

2.2 自整角机

自整角机是通过定、转子之间的电磁感应作用，将输入轴的机械转角转换为和这个转角成一定函数关系的电信号，或将输入的电信号转换为成一定函数关系的机械转角。以电的联系，使远距离的两根或多根机械转轴能够精确地保持相同的转角变化，或者同步旋转，实现角度位置的远距离传输、转换和指示。

自整角机是应用最早的一种重要轴角测量元件，且在早期的同步随动系统中广泛应用，如飞机、舰船等的角度、位置、高度指示与控制；火炮控制、雷达天线定位；轧钢机轧辊控制和指示；核反应堆的控制棒指示器等。在现代永磁交流伺服系统中已很少采用自整角机。

2.3 测速发电机

测速发电机是利用电磁作用原理直接检测速度，它将输入的运动速度转换成电信号输出，其输出的电信号（电压的幅值或频率）与输入的运动速度（旋转运动的转速或直线运动的线速度）呈线性函数关系。它是一种常用速度传感器，有直流测速发电机和交流测速发电机两种。当输出信号不是以电压幅值而是以电压频率来反映转速时称为脉冲测速发电机。

直流测速发电机的输出电压在一定转速范围内与转子转速呈线性关系，当转速方向发生改变时输出电压的极性随之改变。以电子换向替代电刷和换向器的直流测速发电机称为无刷直流测速发电机。有刷直流测速发电机多用于上世纪流行的直流伺服系统中，而早期模拟控制的永磁交流伺服系统中一般采用的是无刷直流测速发电机作为速度传感元件。交流测速发电机是用于传统的两相交流伺服系统的速度检测元件，永磁交流伺服系统中基本不采用这类传感器。

测速发电机在伺服系统中主要是作为速度信号检测及反馈。随着数字控制技术的发展，输出模拟信号的测速发电机已经很少应用在现代高性能永磁交流伺服系统中。

2.4 编码器

编码器是现代高性能永磁交流伺服系统中最常用的传感器之一，是一种机械与电子紧密结合的精密测量元件，它通过光电原理或电磁原理将一个机械的几何位移量转换为电子信号（电子脉冲信号或者数据串），电子信号连接到控制系统（PLC、高速计数模块、变频器等），控制系统经过计算便可以得到测量的数据，构成伺服系统的反馈环节。主要用来检测机械运动的速度、位置、角度、距离或计数。

编码器按结构有旋转式和直线式之分，按检测原理可分为光电编码器、磁性编码器、感应式编码器和电容式编码器。按编码方式可分为增量式编码器、绝对式编码器和混合式编码器。感应式和电容式编码器在永磁交流伺服系统中较少应用，本文不做介绍。

2.4.1光电编码器

光电编码器是一种通过光电转换将输出轴上的机械几何位移量转换成脉冲或数字量的传感器。直线式光电编码器又称线性编码器或光栅尺，通常应用于机床、加工中心以及直线运动的设备中作直线位移检测。本文主要介绍永磁交流伺服系统中常用的旋转式光电编码器。

典型的旋转式光电编码器由码盘、检测光栅、光电转换电路（包括光源、光敏器件、信号转换电路）、机械部件等组成。如图8所示。

图8 光电编码器主要结构图Fig.8 Structure of optical encoder

伺服电机运行过程中，光栅盘与电机同轴或按一定转速比进行旋转，经过光电二极管等电子元件组成的检测装置检测输出若干脉冲信号，并通过计数器等脉冲接收电路来获取电机当前的位置与转速。

下面按增量式、绝对式和混合式分别简单介绍。

（1）增量式光电编码器。增量式光电编码器是利用光线扫描转动的等分分度码盘，通过检测统计信号的通断数量来计算旋转角度的位移量。每产生一个输出脉冲信号就对应于一个增量位移，但不能通过输出脉冲区别出是在哪个位置上的增量。其作用是提供一种对连续位移量离散化或增量化以及位移变化（速度）的传感方法，它能够产生与位移增量等值的脉冲信号，它是相对于某个基准点的相对位置增量，不能够直接检测出轴的绝对位置信息。在系统掉电后旋转角度数据会丢失，上电后需重新复位后才能开始测量。

一般来说，增量式光电编码器有三个输出信号，分别称为A、B和Z。A、B两相为互差90°电度角的脉冲信号（即所谓的两组正交输出信号），从而可方便地判断出旋转方向；Z 为用作参考零位的标志（指示）脉冲信号，在码盘上事先规定一个基准零点，称为零位。当码盘转到零位时，输出一个参考脉冲，称为零位脉冲。码盘每旋转一周，只发出一个标志信号。Z标志脉冲通常用来指示机械位置或对积累量清零。

增量编码器A、B输出的波形一般有两种，一种是有陡直上升沿和陡直下降沿的方波信号；一种是缓慢上升与下降，波形类似正弦曲线的 Sin/Cos曲线波形信号输出。增量式光电编码器输出波形如图9所示。

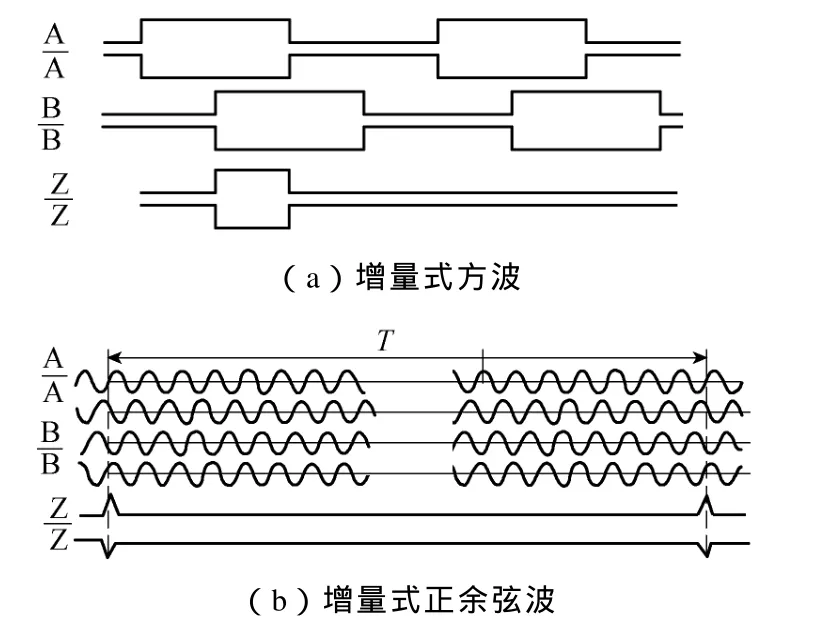
图9 增量式光电编码器输出波形图Fig.9 Output wave of incremental optical encoder

增量式光电编码器的主要技术指标有分辨率、精度、输出信号的稳定性、响应频率、信号输出形式等。

分辨率是指编码器可读取并输出的最小角度变化，用每转刻线数（line）、每转脉冲数（P/r）、最小步距、位等来表示。一般的交流伺服电机控制系统中选用较多的分辨率为 2 500线。对光电转换信号进行逻辑处理，可进一步提高分辨率，方波可做4倍频输出，正余弦波形可通过后续电路读取波形相位的变化，用模数转换电路来细分，5倍、10倍、20倍，甚至100倍以上，细分好后再以方波波形输出。目前增量式光电编码器的最高分辨率可达每转数万脉冲数。

精度是指编码器输出的信号数据对测量的真实角度的准确度。精度通常用角度、角分或角秒来表示。光学、机械、电气以及使用中的安装等因素都将对编码器的精度产生影响。高精度光电编码器精度可高达0.05″。

响应频率是指编码器电气上最大能响应的频率数，如果在高于这个参数的频率下使用，编码器内部电路会无法响应，将导致输出波形严重畸变，甚至产生丢失脉冲的现象。编码器输出的响应频率取决于光电检测器件、电子处理线路的响应速度。

（2）绝对式光电编码器。绝对式光电编码器的基本原理及组成部件与增量式光电编码器基本相同，也是由光源、码盘、检测光栅、光电检测器件和转换电路组成。绝对式编码器是用光线扫描旋转码盘上的专用编码码道，以确定被测物体的绝对位置，然后将检测到的编码数据转换为电信号以脉冲的形式输出测量的位移量。编码的形式有格雷码，BDC码和二进制码等。绝对式编码器的码道及编码如图10所示。

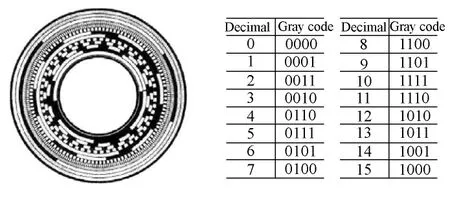
图10 绝对式编码器码道及编码Fig.10 Code channel and code of absolute encoder

与增量式光电编码器不同的是，绝对式光电编码器用不同的数码来分别指示每个不同的增量位置，它是一种直接输出数字量的传感器。在它的圆形码盘上沿径向有若干同心码道，每条上由透光和不透光的扇形区相间组成，相邻码道的扇区数目是双倍关系，码盘上的码道数就是它的二进制数码的位数，在码盘的一侧是光源，另一侧对应每一码道有一光敏元件；当码盘处于不同位置时，各光敏元件根据受光照与否转换出相应的电平信号，形成二进制数。这种编码器的特点是不要计数器，在转轴的任意位置都可读出一个固定的与位置相对应的数字码。显然，码道越多，分辨率就越高，对于一个具有N位二进制分辨率的编码器，其码盘必须有N条码道。绝对式光电编码器原理如图11所示。

绝对式编码器可以直接读出角度坐标的绝对值；没有累积误差；电源切除后位置信息不会丢失；绝对式编码器的精度取决于位数，高精度的绝对式编码器位数可达27位；最高转速比增量式光电编码器高。

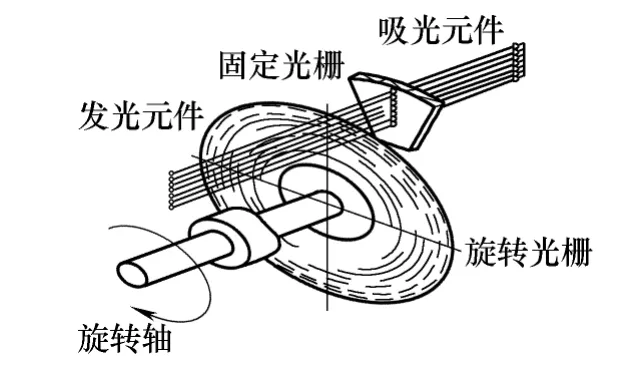
图11 绝对式光电编码器原理图Fig.11 Principle of absolute encoder

绝对式编码器的输出波形如图12所示。

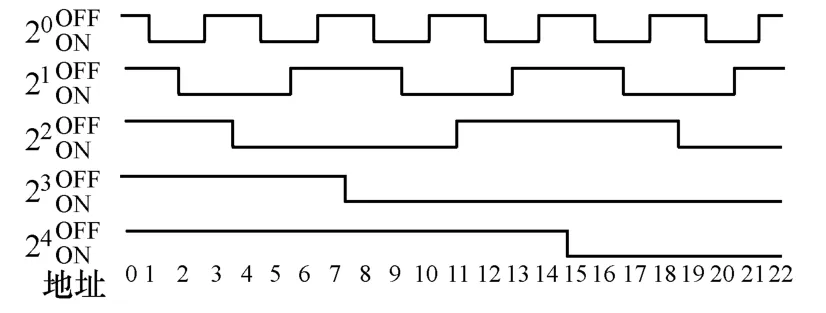
图12 绝对式编码器的输出波形图Fig.12 Output wave of absolute encoder

普通的绝对式光电编码器多为单圈式，它所能测量轴角的范围是0°～360°，不具有多转检测能力，因而不适应多转数运动控制中检测绝对位置的要求。伺服系统采用绝对式光电编码器时应选择多圈式的。多圈式绝对编码器是运用钟表齿轮机械的原理，当中心码盘旋转时，通过齿轮传动另一组码盘（或多组齿轮，多组码盘），在单圈编码的基础上再增加圈数的编码，以扩大编码器的测量范围。

（3）混合式光电编码器。混合式光电编码器用光线扫描转动的复合分度码盘，同时输出绝对旋转角度编码和相对旋转角度编码。伺服系统中常采用此种混合式编码器，当伺服电机旋转时，它输出两组信号，一组信号是与增量式光电编码器完全相同，用于检测伺服电机的有关转速、转向、原点位置及相对角位移的数字信号A、B、Z；另一组信号是用于检测伺服电机磁极位置的数字信号 U、V、W，带有绝对信息输出功能。三路 U、V、W脉冲彼此相位相差 120°，每转的脉冲个数与电机的极对数一致。

混合式光电编码器输出信号波形如图13所示。

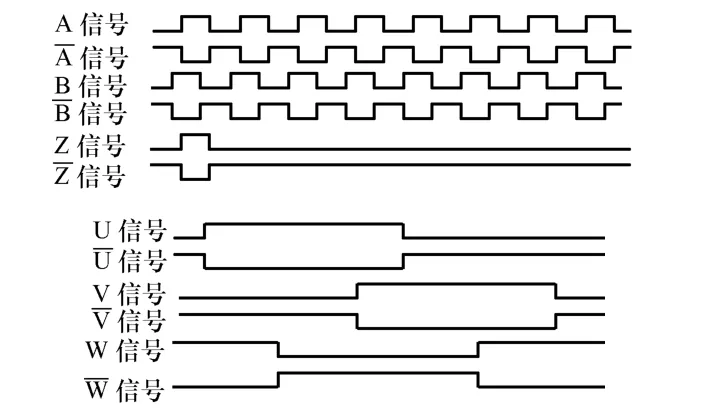
图13 混合式光电编码器的输出信号波形Fig.13 Output signal of hybrid optical encoder

2.4.2磁性编码器

磁编码器是一种新型的角度或位移测量装置，其原理是采用磁敏元件对磁性材料的角度或位移值变化来进行测量。当磁性材料角度或位移发生变化时，将引起磁敏元件的电阻或者输出电压相应变化，通过放大电路对变化量放大后，经单片机处理输出脉冲信号或者模拟信号，达到测量角度或位移的目的。磁性编码器一般可以分为两种：磁电式编码器和磁阻式编码器。

（1）磁电式编码器。图14是一种新型磁电式编码器，由一块圆柱型永磁体及一个集成电路芯片组成。其工作原理是当永磁体随电机转子旋转时，阵列排列于芯片中心周围的霍尔传感器将检测出永磁体的磁场强度分布，并传输反应磁场分布的电压信号。霍尔传感器阵列输出的正弦和余弦电压将随着永磁体转角位置的变化而变化，输出电压信号被细分器转换为绝对角度位置，以需要的输出格式输出。目前这种磁电式磁性编码器分辨率可达15位。

图14 磁电式编码器Fig.14 Magnetic encoder

这种磁性编码器结构简单、防尘能力强，可靠性高，寿命长，价格低廉，体积小，重量轻，安装调试方便，现已广泛应用于永磁交流伺服系统中。

西微微电机研究所研制的磁电式编码器主要基于奥地利微电子的 AS5040芯片和英国雷尼绍公司的 AM4096芯片。采用 360°非接触式角度位置编码；有八种分辨率可供选择；零点可任意设定，调零方便；有增量（A、B、Z）、同步串行接口（SSI）、伺服电机复合码盘（U、V、W、A、B、Z）、转速器、模拟量正弦波等多种输出方式；其转速最高可达 60 000r/min；可选 3V或 5V电源；工作温度范围大，可达-40～125℃。

西安微电机研究所研制的该类编码器已推广应用于电动汽车、机器人等使用的永磁交流伺服系统和其他高分辨率要求的设备中。

（2）磁阻式编码器。磁阻式编码器是一种基于磁阻效应的编码器。主要构成部分有磁阻元件、磁鼓、信号处理电路。磁阻式编码器的典型结构如图15所示。

图15 磁阻式编码器的典型结构图Fig.15 Structure of variable reluctance encoder

在磁记录圆盘（即磁鼓）表面涂覆上按规律排列的某种磁性材料，当磁鼓转动时将会引起周围空间磁场的变化，用磁敏元件去检测磁鼓周围磁场的变化就可获取到相应的角度位置信息。磁阻式编码器又分为 AMR传感器（强磁合金薄膜材料各向异性磁阻）和GMR传感器（巨磁阻）。

磁性编码器与传统的光电式编码器相比，突出的优点是：环境适应能力强，抗振动、耐高温、耐油污、功耗低、结构简单、成本低廉、响应速度快，可应用于传统的光电编码器不能适应的领域，非常适用于高速旋转运动场合使用。缺点是目前制成高分辨率有一定的困难[3]，但相信随着电子技术的发展，分辨率和精度的提高只是时间问题。

尽管在目前市场上的编码器中，光电编码器占有很大的份额，但由于磁性编码器的一些独特优点，加上其成本低廉，近年来在高精度伺服电机控制领域的应用不断增加，如纺机、数控机床、机器人、甚至是军工领域都已有典型的应用。因此磁性编码器已经成为发展高技术产品的关键技术之一，各国都将磁性编码器作为高技术产品加以重点研究。

2.5 霍尔传感器

霍尔元件是一种利用霍尔效应原理制成的半导体磁敏元件。通常将霍尔元件、放大器、温度补偿电路、输出级、电源稳压电路等制作在同一硅片上，然后用陶瓷或塑料封装，称为霍尔效应位置传感器。按输出的不同，可分为开关型霍尔传感器和线性型霍尔传感器两种。

（1）开关型霍尔传感器。开关型霍尔传感器一般为低成本的锁定型开关霍尔，其输出为数字量，只有两个状态，即高逻辑电平和低逻辑电平，当外磁场强度变化时，输出逻辑状态会翻转，利用它可以检测到磁场强度的过零点。因此，在电机的适当位置上安装开关霍尔，当电机旋转时，开关霍尔就会输出与磁场过零点相对应的方波信号。这种传感器在无刷直流电机中应用较多，由于在永磁交流伺服电机中，需要连续的转子位置信号来完成电机的控制，因此，在使用这种传感器时还需要结合开关霍尔位置区间进行位置预估，这种方法又被称为准无位置传感器法[4]。在伺服控制性能要求不高的伺服系统中，采用开关霍尔传感器具有高的性价比。

（2）线性型霍尔传感器。线性型霍尔传感器能够输出正比于磁场强度的霍尔电压，在一定磁感应强度范围内，其输出电压与外磁感应强度呈线性关系，它输出模拟量。永磁交流伺服系统中基于线性霍尔传感器的转子位置检测技术就是利用线性霍尔传感器，提供电机气隙磁场的一些特定变化的信息，通过三角函数运算，单独或利用系统中的控制芯片（DSP）进行R/D解码后得到电机的转子位置信号。线性霍尔传感器能够实时的跟踪转子位置的信息，从而实现了转子位置的检测，但是分辨率较差[4,5]。因此，线性霍尔传感器也只应用于对分辨率要求不高的低成本伺服系统中。

2.6 非机械量检测传感器

除了前述用以检测速度及位置等机械量信息的主要传感器外，在伺服系统中还常采用一些重要的非机械量传感器，如温度传感器、电压传感器、电流传感器等，用来检测系统过电压、过电流及过热，以确保伺服系统能安全可靠的运行。本文仅简单介绍温度传感器。

温度传感器分接触式传感器和非接触式传感器两大类，永磁交流伺服电动机中采用的多为接触式温度传感器。接触式温度传感器的种类很多，经常使用的有热敏电阻、热电阻和热电偶。

（1）热敏电阻。半导体热敏电阻按半导体电阻随温度变化的典型特性分为三种类型：①负温度系数热敏电阻（NTC）；②正温度系数热敏电阻（PTC）；③临界温度系数热敏电阻（CTR）。CTR在某一特定温度下电阻值会发生突变，主要用作温度开关。在温度测量中，则主要采用NTC。热敏电阻的测温范围是-80～+200℃。

（2）热电阻传感器。热电阻传感器主要是利用电阻值随温度变化而变化这一特性来测量温度及与温度有关的参数。目前较为广泛的热电阻材料为铂、铜、镍等，它们具有电阻温度系数大、线性好、性能稳定、使用温度范围宽、加工容易等特点。由于铂具有很好的稳定性和测量精度，故人们主要把它用于高精度的温度测量和标准测温装置。常用的铂电阻有 Pt50、Pt100、Pt300、Pt1000等。铂电阻的测温范围是-200～+850℃。

（3）热电偶。两种不同的金属A与B形成闭合回路，当两个接点温度不同时回路将产生电势，该电势的方向和大小取决于两导体的材料及两接点之间的温度差，而与导体的粗细、长短无关。这种现象称为热电效应，组成的测量传感器称为热电偶。常用的热电偶有铂－铂铑、镍铬－镍硅、镍铬－康铜等。热电偶的测温范围很宽，可测量-270～+1 600℃范围内的温度，按测温范围又分为K、E、J、T、B、R、S等型。

总之，温度传感器不但种类繁多，而且组合形式多样，应根据不同的场所选用合适的产品。

3 无位置传感器技术

旋转变压器、编码器等位置传感器虽然为永磁交流伺服电机系统提供了最直接有效的检测方法，但它也使伺服系统增加了体积，更增加了伺服电机系统的制造工艺难度和成本。同时，安装这些传感器后也带来了一些可靠性方面的问题，在某些特殊环境下，位置传感器也不符合集成应用系统的要求。因此，随着控制技术的不断进步以及数字信号处理器等一些新元器件的出现，无位置传感器控制技术在交流伺服系统中获得了广泛应用和发展，尤其DSP的高速信息处理能力使无位置传感器控制技术的复杂算法能得以实现。

无位置传感器控制系统是指利用电机绕组中的有关电信号，通过适当方法估计出转子的电气和机械位置以及转速等，从而取代传感器，实现电机的闭环控制。永磁交流伺服电机系统是一个多变量，强耦合的非线性系统，人们将现代控制理论、非线性理论和一些其他领域的研究成果应用于永磁交流伺服电机无位置传感器控制系统中，提出了较为可行的方法。这些估计方法大体可分为两类：①基于电机电磁关系的位置估计方法；②基于各种观测器的位置估计方法。基于电机电磁关系的位置估计方法有：直接检测定子三相端电压和电流，利用它们计算出转子位置角和转速；检测电机相电感的变化来估计转子位置；检测电枢绕组反动电势过零点来判断转子位置的反电动势法；通过计算定子磁链来估计转速和转子位置的方法等等。基于各种观测器的位置估计方法的实质是状态重构，其原理是重新构造一个系统，利用原系统中可直接测量的变量作为它的输入信号，并使其输出所需信号的方法。如扩展卡尔曼滤波法、全阶状态观测器法、模型参考自适应法、滑模变结构法、基于人工智能理论的各种估算方法等等[6,7]。随着新技术的发展，不断还有新的无位置传感器转子位置检测理论及方法的提出，无位置传感器技术将会得到越来越广泛的应用。以下简单介绍几种无位置传感器的转子位置估算方法。

（1）瞬时电压方程法。利用电动机各相瞬时电压和电流方程，实时计算电动机由静止到正常运转任一时刻转子的位置，控制电动机的运行。该方法不需专门的起动线路，电路简单，起动转矩大，但对电动机本体的数学模型依赖性大，当电动机参数因温度变化发生漂移时，容易造成建模误差，使精确度受到影响。另外，由于在线计算复杂，计算量很大，考虑到转子位置检测的实时性，必须采用具有快速运算能力的DSP和高速A-D转换器[3]。

（2）反电动势法。反电动势法是最常用的无刷电机（BLDC）无传感器控制方法，其基本原理是通过检测各相绕组反电动势的过零点来判断转子磁极的换相位置。对于常见的两相导通三相六状态工作方式，除了换相的瞬间之外，在任意时刻，电动机总有一相绕组处于断电状态。当断电相绕组的反电动势过零之后，再经过 30°电角度，就是该相的换向点。因此，只要检测到各相绕组反电动势的过零点，就可以确定电动机的转子位置和下次换流的时间。反电动势法有两个主要缺陷：当电动机在静止或低速运行时，反电动势为零或太小，因而无法利用；又由于该方法在原理上作了近似处理，忽略了电枢反应和滤波产生的反电动势过零点与实际转子位置不一致，因而需要采用相应的误差补偿措施[8]。

（3）高频信号注入法。通过检测基波反电动势来获得转子位置的方法虽然简单，但仅适用于高速运行时，在零速或低速时会因检测不到反电动势而不适用。高频信号注入法则是利用电动机的凸极效应来追踪转子位置的一种方法，可以在全转速范围内有效地检测转子的空间位置。其基本原理是在电机中注入特定的高频电压（电流）信号，然后检测对应的电流（电压）信号以确定转子的凸极位置，多采用的是高频电压信号注入，且注入的高频电压信号可为旋转高频电压信号或脉动高频电压信号。

旋转高频电压注入法是在基波上叠加一个三相平衡的高频电压激励信号，然后检测对应的高频电流响应并通过特定的信号处理来获取转子位置信息。此种方法主要应用于凸极率较大的永磁体内置式电机。脉动高频电压注入法只是在估计转子旋转坐标系中的直轴上注入高频正弦电压信号，该信号在静止坐标系中是一个脉动电压信号，更适用于凸极率较小的表贴式电机。两种方法相比较，脉动高频电压注入法跟踪精度高，静态和动态性能更好，无需对转子位置估算角度进行补偿。旋转高频电压注入法的转子位置检测系统较为复杂，转子位置估算角度需作相位补偿，且转子位置信息提取过程的算法对系统的动态性能影响较大，但其转子位置检测系统自成一体，因此更易于调试和实现[9,10]。

（4）模型参考自适应法。模型参考自适应法是一种较常用的估算转子位置和速度的方法，模型参考自适应辨识的主要思想是将含有待估计参数的方程作为可调模型，将不含未知参数的方程作为参考模型，两个模型具有相同物理意义的输出量。两个模型同时工作，并利用两个模型输出量的误差根据适合的自适应律来实时调节可调模型的参数，以达到控制对象的输出跟踪参考模型输出的目的。当差值为零时，可认为此时估计的转子位置为真实位置[11]。模型的选取和电机参数的变化会直接影响转速辨识，运算的繁琐也可能会使辨识与调整跟不上扰动变化，可通过采用高速DSP并与其他控制技术相结合（如结合高频信号注入法等）来改善控制效果。

（5）滑模变结构控制。滑模变结构控制是一种非线性控制，在PMSM中该方法是基于给定电流与反馈电流间的误差来重构电机的反电动势，估算转子速度。滑模变结构控制的本质是滑模运动，通过结构变换开关，以很高的频率来回切换，快速修正反电动势，使估算电流和实际电流相等。滑模运动与控制对象的参数变化以及扰动无关，具有很好的鲁棒性。滑模变结构控制由于其鲁棒性强、动态响应快、易于工程实现等优点得到了广泛的应用，但由于其本质上是不连续的开关控制，不可避免会引起系统发生抖振，应用时应采取合适的方法来削弱和抑制抖振。同时因该方法是通过观测电机的反电动势来得到转速，低速时不能得到很好的控制效果[12,13]。

（6）扩展卡尔曼滤波（EKF）法。扩展卡尔曼滤波（EKF）法是一种基于最小方差的最优状态预测估计方法，将线性系统状态估计的卡尔曼滤波算法应用于永磁交流伺服电机这种非线性系统中，以迭代法为基础，实现对PMSM的非线性最优状态估计。结合卡尔曼滤波原理，首先通过测量逆变器直流母线电压，再利用DSP生成的SVPWM控制信号，检测电机定子三相电压值与电流值，对三相电压、电流值进行坐标变换后输入扩展卡尔曼滤波器中，经过扩展卡尔曼滤波运算得出调速系统的状态估计值（转速和电机转子位置角信息），来代替机械式位置传感器测量的转子位置和转速，并用于矢量控制和速度反馈。与其他方法相比，扩展卡尔曼滤波（EKF）法能有效抑制系统误差和测量误差对状态估计的影响，状态估计精度高、收敛速度快，是无传感器控制方法中较好的速度观测方法[13-15]。

（7）神经网络控制法。神经网络是一种大规模并行的非线性动力学系统，它采用工程技术方式模拟人脑神经网络的结构和功能，可以充分逼近任意复杂的非线性关系，具有信息的分布存储、并行处理以及自学习能力。随着现代智能控制技术的发展，利用人工神经网络与各种算法相结合来进行永磁交流伺服系统无传感器转子速度和位置辨识已取得可喜的成果。如与传统的PID控制相结合，神经网络被用来精确估计位置及转速；与模型参考自适应控制相结合，将神经网络控制器用作自适应速度控制器；与小波技术相结合，采用鲁棒小波神经元控制；将神经网络广义逆算法引入模型参考自适应的控制策略等等[16-18]。

（8）模糊控制。模糊控制是将模糊数学的基本理论应用于工程实践中，它不需要建立被控对象的精确数学模型，能够简化系统设计的复杂性，特别适应于解决非线性、时变及滞后、模型不完全的系统问题，具有适应能力强，系统的鲁棒性强，规则和参数整定方便等优点。对于PMSM这种多变量、较难建立精确模型的复杂系统，模糊控制技术将有很大的发挥空间。但它也存在难以达到较高的控制精度，模糊控制规则难以确定，缺乏系统而有规律的模糊规则设计方法等缺点，使用中对控制专家的经验依赖性较大，这个特点既是优点也是缺点。同神经网络一样，模糊控制的应用更多的是与其他控制算法相结合，如与滑模控制相结合，与遗传算法相结合，与神经网络相结合等等[19-21]。

无位置传感器的永磁交流伺服电机控制系统，免去传感器安装和维护的不便，提高了系统的可靠性，降低了成本。在越来越多的场合，无位置传感器控制技术应用基本可以取代部分有传感器的伺服系统，实现无传感器运行。无传感器技术采用的位置估算方法种类很多，各有不同的优缺点和适应范围，经常是几种方法联合使用，以求得到更佳的控制效果。但还存在较多的问题需要解决，比如算法复杂，需要有高精度的数字信号处理器；受电机参数影响较大；检测精度低，如上面介绍的前几种方法实际上只是检测到了电机转子的磁极位置，而速度的检测精度以及机械位置的精度都不是很高；低速时运行性能较差，无传感器控制还很难在电机（非凸极）静止时从电机的电气特性获得转子的初始位置。只有电机起动到一定的转速后，才能将电机切换至无位置传感器运行状态，电机初始转子位置检测和起动问题仍然是永磁交流伺服电机无传感器运行有待解决的难题之一。总的来说，在高精度的伺服驱动场合，无位置传感器的伺服系统还很难取代有位置传感器的伺服系统。

4 伺服系统用传感器现状及发展趋势

编码器与旋转变压器是目前永磁交流伺服系统中应用最多的两类角位传感器。

在国内市场上，编码器的技术及产品发达国家具有明显优势，欧美厂商牢牢占据高端市场，市场占有量达40%，产品价格昂贵，主要以HEIDENHAIN（海德汉）、RENISHAW（雷尼绍）等品牌为代表；日韩厂商占据中端市场，市场占有量约 35%，以TAMAGAVA（多摩川）、KOYO（光洋）等为代表；国内品牌多为低端产品，市场占有量约25%，主要有长春光机所等。

旋转变压器的技术及产品则是国内外水平相当，国外品牌主要有日本TAMAGAVA（多摩川）、日本MINEBEA（美蓓亚）；德国LTN；美国HAROWE（丹纳赫集团下属公司）等。国内主要制造厂商有西安微电机研究所等。

近年来，交流伺服系统处于蓬勃发展阶段，正朝着智能化方向快速发展，每年都有先进的技术展现。伺服控制系统中的各个组成部分相应的也有了飞速发展，传感装置与技术也无例外。新型传感器发展的总趋势是微型化、多功能化、高精度化、智能化、网络化和高可靠性以及无传感器技术等[22]。

从结构上来讲，追求的是多样化，即针对不同使用场合及不同电机结构时传感器结构及外形可以是千变万化的；在伺服控制精度要求不高时，传感器注重的是简单化，即尽可能简化以求高性价比，如仅一个简单芯片或霍尔片，以提高产品竞争力；在一体化和集成化方面，传感器的部分功能可以集成在驱动器的芯片甚至利用软件来实现，比如DSP等；通信的总线化，采用通用或专用通信协议来实现传感器的网络化；传感器精度和分辨率是保障伺服系统性能的关键因素之一，因而高精度和高分辨率是传感器永恒的追求，如光电编码器分辨率已达到229，还要追求更高，无刷旋变精度从目前的角分级追求达到角秒级，磁编码器有望超过 217等等；为适应伺服系统的高速化，传感器还需要在机械结构强度、对频率的响应速度以及信号的处理速度等多方面尽量优化，以提高响应频率及自身结构对高速的适应性；高可靠性发展将体现在传感器的抗干扰能力、无刷化结构、多余度设计等方面，如磁阻旋变、磁性编码器以及LVDT等就是一类具有高可靠性优势的产品；除此之外，新工艺、新材料、新器件、新结构以及新原理的不断研究和应用，也将促使传感器在精度、分辨率、稳定性及可靠性等各方面得以有效提升[23]。

无传感器技术的发展将体现在新理论、新方法、新算法的不断涌现，以提高控制精度并改善其控制性能；同时各种算法的互相结合及优势互补将使无位置传感器控制更加完善；新的高速处理器件的出现也将进一步促进无传感器技术取得长足的发展。

[1] GB/T 7665-2005传感器通用术语[S]. 北京: 中国标准出版社, 2005.

[2] 西安微电机研究所编. 实用微电机手册[M]. 沈阳:辽宁科学技术出版社, 2003.

[3] 中国电气工程大典编辑委员会编. 中国电气工程大典, 第9卷, 电机工程[M]. 北京: 中国电力出版社,2008.

[4] 叶伟. 适应于高速永磁电机的多模式转子位置检测技术研究[D]. 哈尔滨: 哈尔滨工业大学, 2010.

[5] 韩安太, 郭小华. 基于线性霍尔传感器的新型交流伺服系统设计[J]. 微电机, 2009(6): 43-47.

Han Antai, Guo Xiaohua. Design of novel AC servo system based on linear hall effect sensors[J]. Micromotors, 2009(6): 43-47.

[6] 于艳君, 程树康, 柴凤. 永磁同步电动机无传感器控制综述[J]. 微电机, 2007, 40(8): 58-61.

Yu Yanjun, Cheng Shukang, Chai Feng. Overview of sensorless control of permanet-magnet synchrounos motor[J]. Micromotors, 2007, 40(8): 58-61.

[7] 李翠萍. 基于卡尔曼滤波的无传感器永磁电机矢量控制研究[D]. 哈尔滨: 哈尔滨工业大学, 2007.

[8] 吴红星, 叶宇骄, 倪天, 等. 无刷电机转子位置检测技术综述. 微电机[J]. 2011(8): 75-81.

Wu Hongxing, Ye Yujiao, Ni Tian, et al. Summary of detecting rotor position technique for brushless DC motor[J]. Micromotors, 2011(8): 75-81.

[9] 秦峰, 贺益康, 刘毅, 等. 两种高频信号注入法的无位置传感器运行研究[J]. 中国电机工程学报,2005, 25(5): 116-121.

Qin Feng, He Yikang, Liu Yi, et al. Comparative investigation of sensorless control with two highfrequency signal injection schemes[J]. Proceedings of the CSEE, 2005, 25(5): 116-121.

[10] 郑泽东, 李永东, Maurice Fadel. 采用Kalman滤波器进行信号处理的高频信号注入法在电动机控制中的应用[J]. 电工技术学报, 2010, 25(2): 54-59.

Zheng Zedong, Li Yongdong, Maurice Fadel. Application of high frequency signal injection method in motor control using Kalman filter for signal processing[J]. Transactions of China Electrotechnical Society,2010, 25(2): 54-59.

[11] 常凯. 基于模型参考自适应的永磁同步电机无速度传感器控制系统的设计[D]. 沈阳: 东北大学, 2009.

[12] 苏健勇, 杨贵杰, 李铁才. PMSM 扩展状态滑模观测器及转子位置和速度估算[J]. 电机与控制学报,2008, 12(5): 524-528.

Su Jianyong, Yang Guijie, Li Tiecai.Extended state sliding mode observer of PMSM and estimation of rotor position plus speed[J].Electric Machines and Control, 2008, 12(5): 524-528.

[13] 朱军, 韩利利, 汪旭东. 永磁同步电机无位置传感器控制现状与发展趋势[J]. 微电机, 2013(9): 11-16.

Zhu Jun, Han Lili, Wang Xudong. Status and trends of sensorless control algorithm for PMSM[J]. Micromotors, 2013, 46(9): 11-16.

[14] 王琛琛, 李永东. 基于EKF的异步电机无速度传感器矢量控制方法[J]. 清华大学学报: 自然科学版,2008, 48(10): 1545-1548.

Wang Shenshen, Li Yongdong. A speed sensorless vector control method of IM using extended Kalman filter[J]. 2008, 48(10): 1545-1548.

[15] Janiszewski, Dariusz. Sensorless control of permanent magnet synchronous motor based on unscented Kalman filter[C]. International Conference on Power Engineering, Energy and Electrical Drives, 2011: 1-6.

[16] 夏常亮, 李志强, 王明超, 等. 基于 RBF神经网络在线辨识的无刷直流电机单神经元PID模型参考自适应控制[J]. 电工技术学报, 2005, 20(11): 65-69.

Xia Changliang, Li Zhiqiang, Wang Mingchao, et al.Single neuron PID model reference adaptive control for PM rushless DC motors based on RBF neural network on-line identification[J]. Transactions of China Electrotechnical Society, 2005, 20(11): 65-69.

[17] 强勇, 凌有铸, 贾冕茜. 基于 RBF神经网络的永磁同步电机速度控制[J]. 微电机, 2013, 46(4): 53-56.

Qiang Yong, Ling Youzhu, Jia Mianqian. Speed control of PMSM based on RBF neural network[J]. Micromotors, 2013, 46(4): 53-56.

[18] 李毓洲, 阳林. 基于小波神经网络的永磁同步电机无速度传感器控制[J]. 微电机, 2010(7): 53-56.

Li Yuzhou, Yang Lin. Speed sensorless control of the permanent magnet sychronous motor based on wavelet neural networks[J]. Micromotors, 2010(7): 53-56.

[19] 许振伟, 蒋静坪, 骆再飞. 模糊模型算法控制的永磁同步电动机位置伺服控制系统[J]. 电工技术学报,2003, 18(4): 99-102.

Xu Zhenwei, Jiang Jingping, Luo Zaifei. Permanent magnet synchronous motor position servo system controlled by fuzzy model algorithmic control[J].Transactions of China Electrotechnical Society, 2003,18(4): 99-102.

[20] 高子龙, 李志刚. 基于模糊控制策略的位置伺服系统研究[J]. 微电机, 2013, 46(1): 67-71.

Gao Zilong, Li Zhigang. Research of position servo system based on fuzzy controller[J]. Micromotors,2013, 46(1): 67-71.

[21] Thiemann P, Mantala C, Mueller T, et al. Sensorless control for buried magnet PMSM based on direct flux control and fuzzy logic[C]. IEEE Symposium on Diagnostics for Electrical Machines, Power Electronics and Drives, 2011: 405-412.

[22] 莫会成, 闵琳, 王健, 等. 现代高性能永磁交流伺服系统综述—永磁电机篇[J]. 微电机, 2013, 46(9):1-10.

Mo Huicheng, Min Lin, Wang Jian, et al. Summarizing commentary on modern high-performance AC servo system—PM servo motor[J]. Micromotors, 2013, 46(9):1-10.

[23] 莫会成, 王健, 任雷. 现代高性能永磁交流伺服系统综述—驱动控制篇[J]. 微电机, 2013, 46(1): 1-8.

Mo Huicheng, Wang Jian, Ren Lei. Summarizing commentary on modern high-performance AC servo system—drive and control[J]. Micromotors, 2013, 46(1):1-8.