海水槽控温波动性及均匀性的概率密度分布分析

艾锐峰，程 杰，欧阳军，杨 健

（中国白城兵器试验中心气象室，吉林 白城 137001）

0 引 言

控温海水槽是温盐深计量测试系统的关键设备。目前，国内外海洋仪器校准实验室均建有高水准的控温海水槽，为温盐深测量仪等海洋水文调查设备的测试、校准工作提供稳定的温度场。温度场的均匀性和波动性是影响温盐深计量测试系统测量不确定度的重要因素。目前其所满足的概率分布尚待确定，测量方法不一。

文献[1-2]对恒温槽的测试和不确定度评定进行了论述。在海水槽测量不确定度的评定中，需要给出其控温波动性和均匀性所服从的概率密度分布[3-4]；但是，目前在实际应用中主要是根据经验给出其温度场均匀性和波动性所满足概率分布的假设，并没有基于测量数据给出其概率分布的严格数学推断，主观性过强，应用于不同海水槽时，存在风险。基于此，本文首先依据JJF 1030——2010《恒温槽技术性能测试规范》[1]对控温海水槽进行测试，录取测量数据；利用χ2检验法[5]对波动性和均匀性满足的概率分布进行统计推断，以严格确定其概率密度分布函数。

1 控温海水槽均匀性及波动性的测试

根据JJF 1030——2010《恒温槽技术性能测试规范》的规定，按下述方法对海水槽进行测量。测量仪器及设备包括海水槽、铂电阻温度计、测温电桥、低热电势转换开关。图1为海水槽的工作区域示意图。

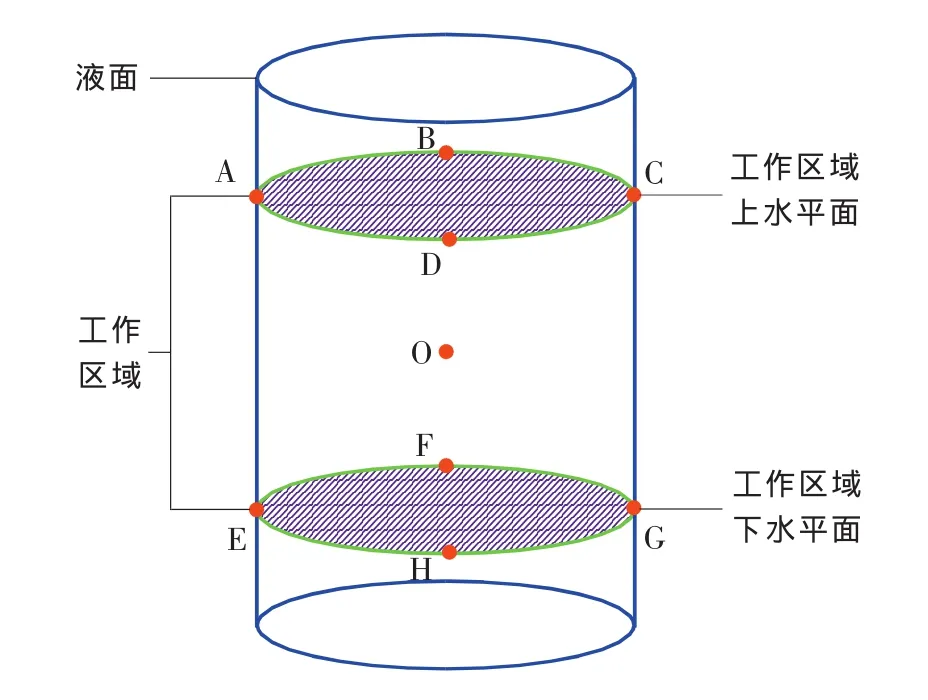
图1 海水槽工作区域示意图

1.1 波动性测试方法

波动性的测试一般选择在海水槽实际工作温度范围的下限或上限进行（-5～35℃）。也可测试工作温度范围其他温度点的波动性。本文以35℃为例。

将海水槽温度设定在35℃，将一支铂电阻温度计插入图1的位置O，即工作区域内1/2深度处，待海水槽到达35℃后稳定一段时间（10min，或者海水槽使用说明书的规定时间）后，利用测温电桥读取铂电阻温度值。

在每1min内按照均匀间隔读取6次或者以上次数的测量值，持续一段时间，获取M个测量值tO，m，m=1，2，…，M（为了利于后续的分布假设检验处理，尽可能获取多的测量数据），作为波动性概率密度分布分析的样本值。

1.2 均匀性测试方法

均匀性测试的温度点同样选取在35℃。测试的位置根据JJF 1030——2010，一般选择在工作区域的上、下水平面上均匀分布的典型位置上。见图1中位置 A，B，C，D，E，F，G，H。 本文以上工作平面为分析对象。

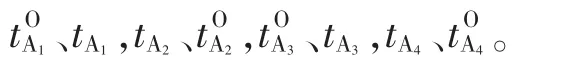
计算位置O铂电阻温度计示值的平均值：

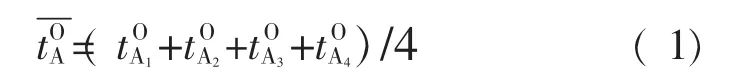
计算位置A铂电阻温度计示值的平均值：

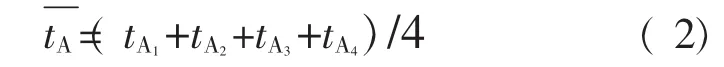
则A点相对于O点的温度示值差为

按同样的方法，测量工作区上水平面其他点相对于 O 点的示值差：tB-O、tC-O、tD-O。

通过循环测量获取 N 个 tA-O，tB-O、tC-O、tD-O的样本值：tA-O，n、tB-O，n、tC-O，n、tD-O，n，n=1，2，…，N 作为工作区上水平面均匀性概率密度分布分析的样本值。合并表示为 tS，n，n=1，2，…，L。

2 概率密度分布的分析方法

对测量数据所满足的分布类型进行推断时，首先根据经验或者由样本数据的直方图给出其分布类型的一个假设。再采用最大似然估计，对分布函数中的未知参数进行估计[6]。最后通过假设检验对其满足的分布类型作出统计推断。

2.1 分布函数的参数估计

首先由测量数据 tO，m，m=1，2，…，M 和 tS，n，n=1，2，…，L 画出 tO、tS的直方图，得到其分布的直观印象。根据数据的直方图，假设tO服从类型为f1（tO，θ1，θ2，…，θr）的概率密度分布，θ1，θ2，…，θr为分布函数的参数；tS服从类型为f2（tS，β1，β2，…，βq）的概率密度分布，β1，β2，…，βq为分布函数的参数。

采用最大似然估计对分布函数的参数进行估计。即寻找使得样本值出现的可能性最大的参数值作为未知参数的估计。

构造似然函数：

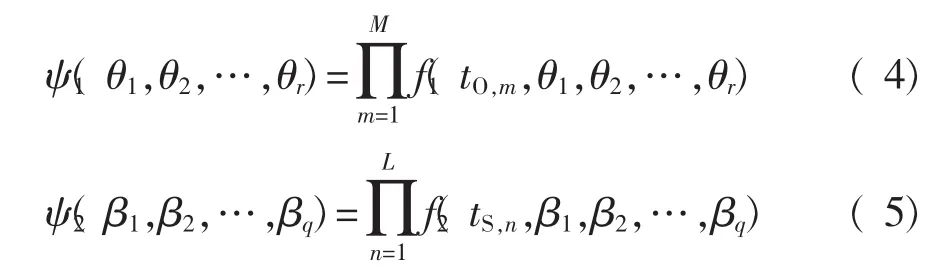
则：

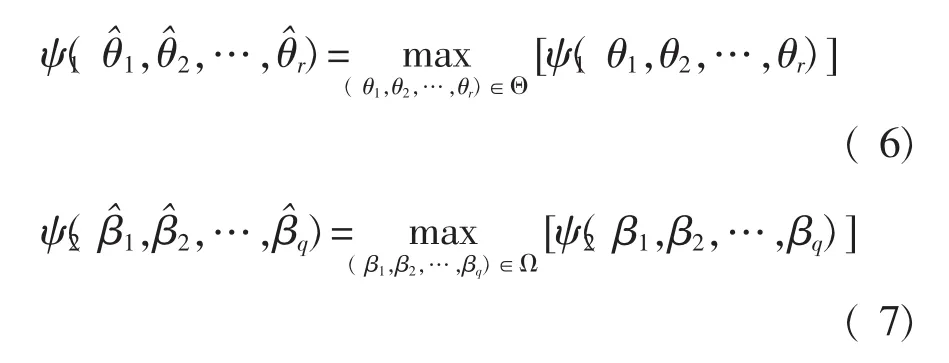
对ψ1（θ1，θ2，…，θr）、ψ2（β1，β2，…，βq）求导，并令其等于0，即：

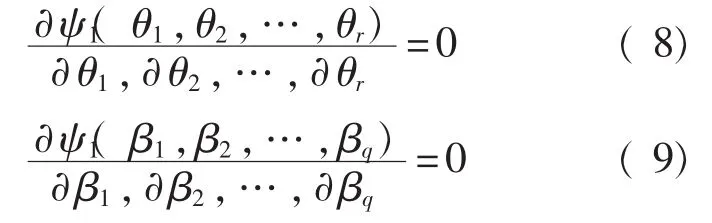
计算对应的（ θ1，θ2，…，θr）、（β1，β2，…，βq）值，使ψ1、ψ2最大的值作为（θ^1，θ^2，…，θ^r）、（β^1，β^2，…，β^q）。

2.2 概率分布的假设检验

对概率分布进行假设检验的常用方法是χ2检验法，它是根据来自总体的样本，检验关于总体分布假设的方法，相对简单并适用广泛[7-12]。

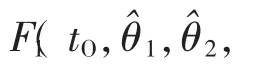
以tO的概率分布的检验为例，先做出二元假设，即：

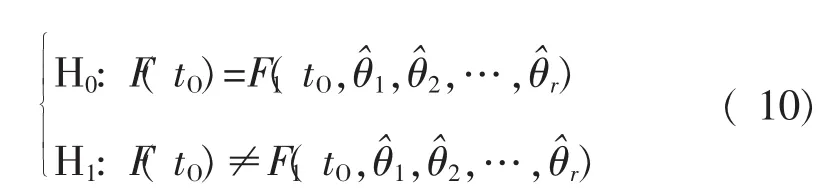
对tO的分布在数轴上顺次划分K个区间：-∞=t0＜t1＜…＜tK-1＜tK=+∞，计算样本 tO，m落入区间[tk-1，tk）（k=1，2，…，K）的频数 fk。 当 H0为真时，tO，m落入[tk-1，tk）的概率为pk=F1（tk，θ^1，θ^2，…，θ^r）-F1（tk-1，θ^1，θ^2，…，θ^r），则相应的频数为 pk·M。构造 χ2分布检验的检验量：

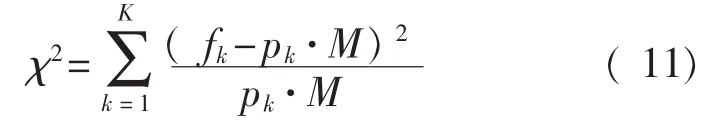
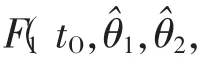
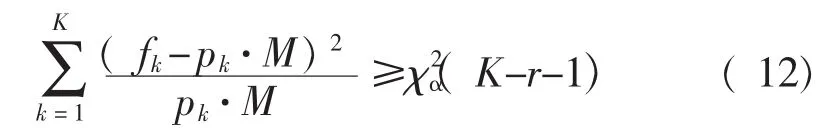
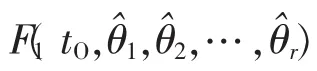
3 测量数据分析

利用海水槽、两支标准铂电阻温度计、测温电桥作为测量设备录取测量数据，依据上述方法进行分析。

3.1 波动性的概率密度分布分析

首先作出海水槽控温波动度的直方图，如图2所示。

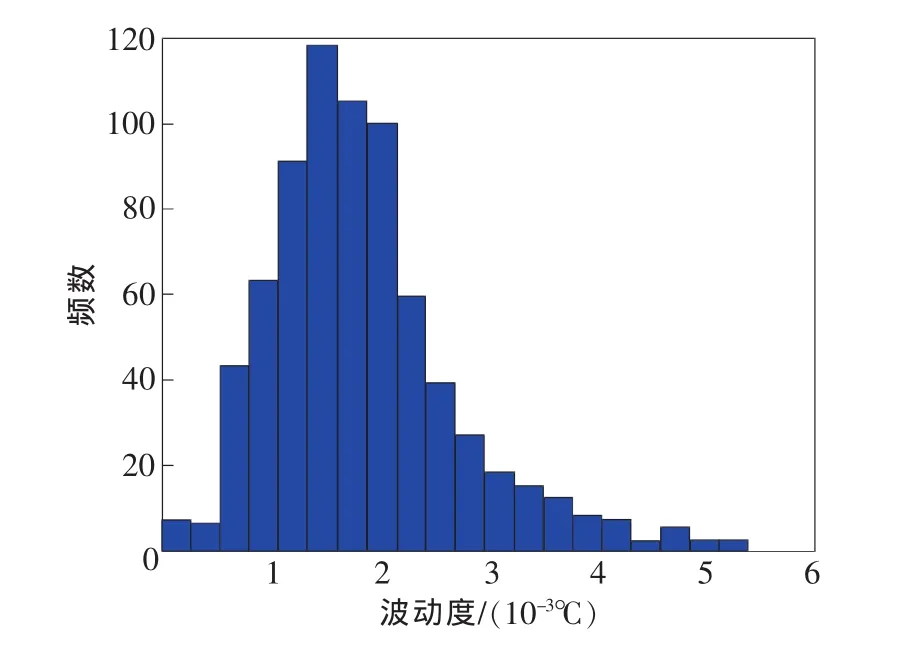
图2 波动度测量数据直方图

从图中可以直观地看出其与Gamma分布或者正态分布接近。选取Gamma分布作为对象，即假设波动度Δt满足下式所示的分布：

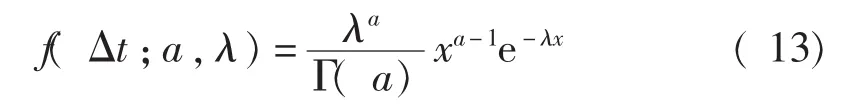
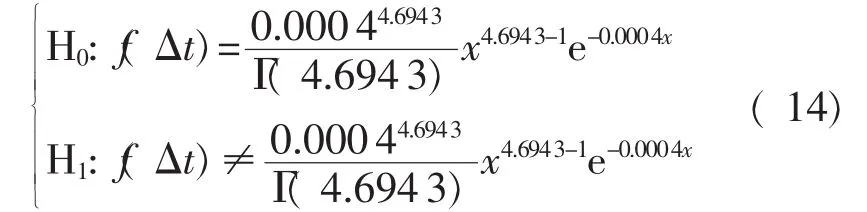
图3、图4分别为测量数据的概率密度分布和Gamma分布假设下的概率密度分布。

首先划分K=20个区间，测量数据M=729个，计算各个区间频数。据χ2检验规则，区间划分应使得pk·M≥5，根据计算结果，对区间进行合并调整，K变为15，最后结果如表1所示。

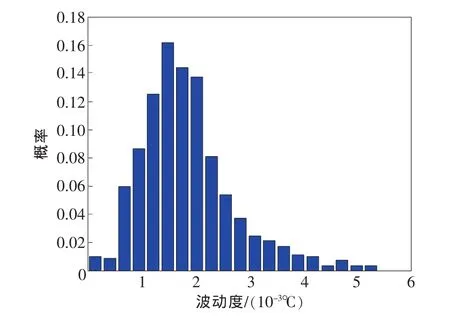
图3 波动度测量数据概率密度分布

图4 Gamma分布假设下的概率密度分布

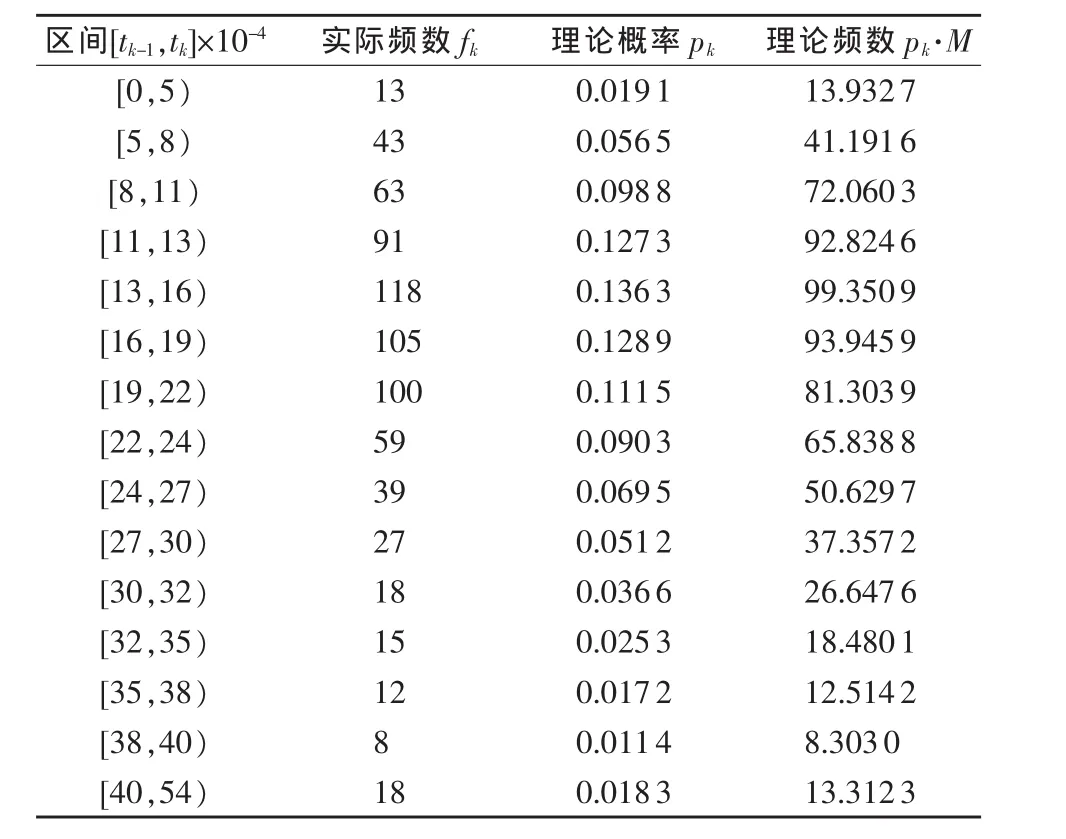
表1 χ2检验计算表

根据表1结果，由式（11）计算检验量得到χ2=20.1274。

在显著水平α=0.05下，有：

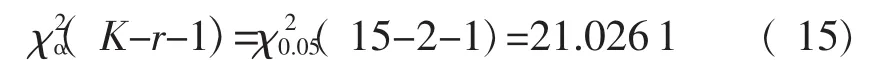
即：χ2=20.1274≤χ20.05（ 12）。因而可以认为在水平α=0.05下接受H0，即波动度Δt服从Gamma分布：

3.2 均匀性的概率密度分布分析

利用均匀性的测量数据，共计M=2729个。首先作出其直方图，如图5所示。选取正态分布作为对象，即假设均匀性Δt′的概率密度分布函数如下式所示：

由最大似然估计得到其参数：μ^=0.0031，σ^=0.0009。图6、图7分别为测量数据的概率密度分布和正态分布假设下的概率密度分布。

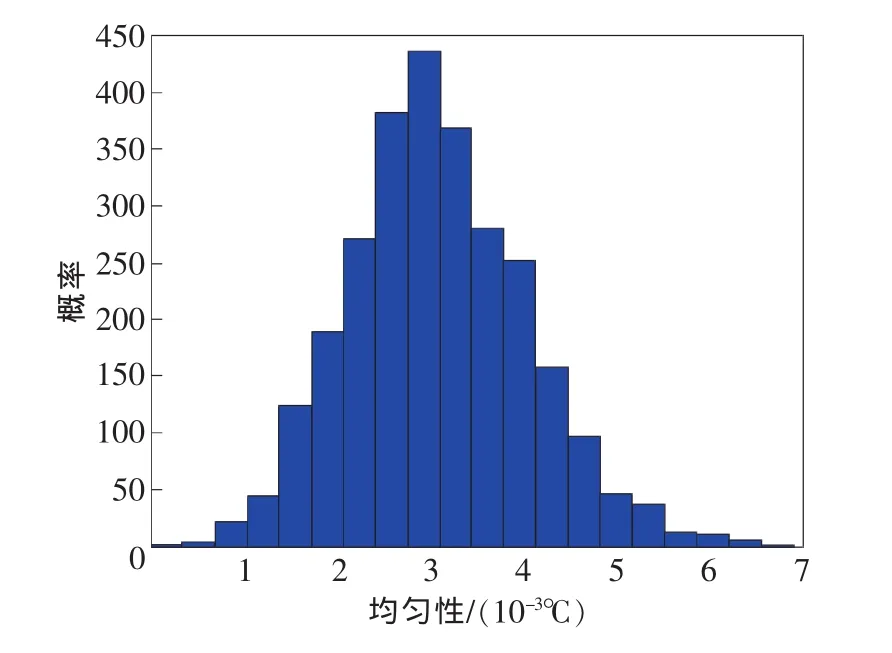
图5 均匀性测量数据直方图

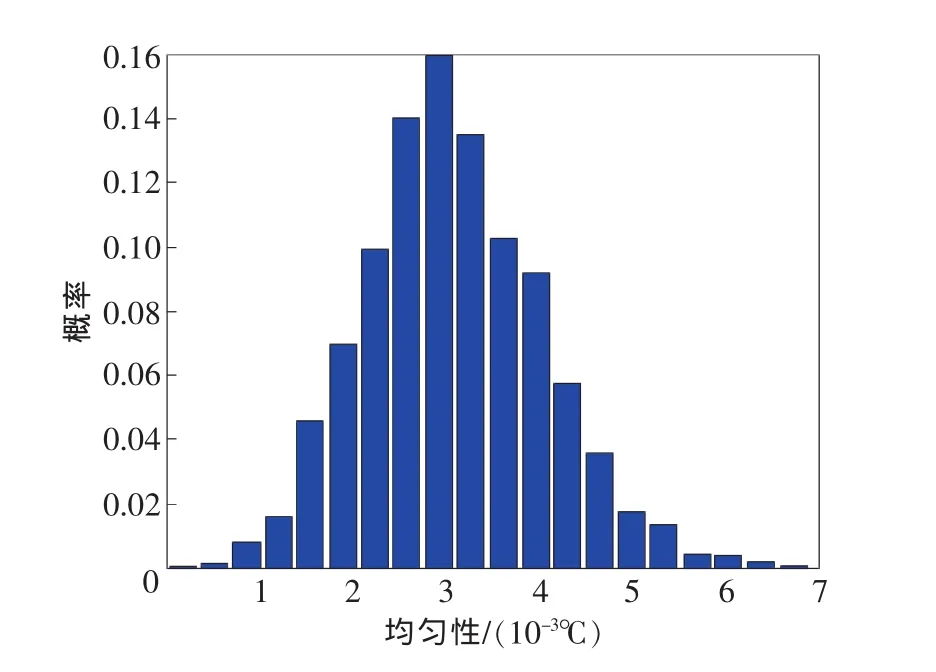
图6 均匀性测量数据概率密度分布

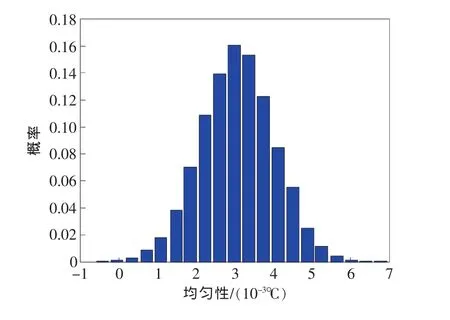
图7 正态分布假设下的概率密度分布

划分K=19个区间，计算检验量得到χ2=24.0256。

在显著水平α=0.05下，有：

即：χ2=24.0256≤（ 16）。因而可以认为在水平α=0.05下接受H0，即均匀性Δt′服从正态分布：

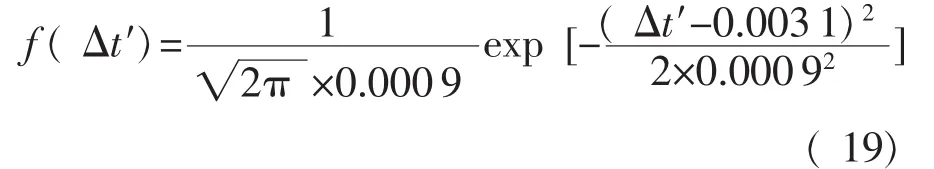
4 结束语

作为温盐深计量测试系统关键设备的控温海水槽，其温度场均匀性和波动性所满足的概率密度分布在实际工作中主要是根据经验给出。本文在测量数据的基础上，利用最大似然估计和χ2检验法[3]给出其严格的统计推断，得到了概率密度函数式。分析中理论分布函数的选取，结合直方图经过反复试验确定。由于χ2检验法依赖于区间的划分，可以在此基础上利用其他假设检验法（如K检验法）做进一步的比对分析。

[1]JJF 1030—2010恒温槽技术性能测试规范[S].北京：中国质检出版社，2010.

[2]郭沈辉，戚晓红，王林虎.恒温槽的校准及不确定度的评定[J].中国测试技术，2007，33（ 6）：86-89.

[3]Gonzalez A，Herrador M.Evaluation of measurement uncertainty in analytical assays by means of monte carlo simulation[J].Talanta，2004，64（ 20）：415-422.

[4]Wübbeler G， Krystek M， Elster C.Evaluation of measurement uncertainty and its numerical calculation by a monte carlo method[J].Measurement Science and Technology，2008，19（ 8）：125-130.

[5]茆诗松，程依明，濮晓龙.概率论与数理统计教程[M].北京：高等教育出版社，2004：79-92.

[6]Ruiz M E，Vicente S P,Ruiz F R.Statistical inference Hypothesis testing[J].International Journal for Clinical and Investigate Allergology and ClinicalImmunology，2010，38（ 5）：266-277.

[7]汤建勋，张斌，许光明.机抖激光陀螺抖动随机噪声概率分布的检验[J].光电子与激光，2003，14（ 1）：105-106.

[8]李广柱，高仲辉，陈少应.风廓线雷达风谱的概率分布研究[J].计算机仿真，2009，26（ 4）：93-96.

[9]邹传仁，张俊芝.基于Bayes方法和模糊检验的年最高水位的概率模型研究[J].浙江工业大学学报，2006，34（5）：571-575.

[10]姜培华，范国良.几种非正态总体未知参数的贝叶斯假设检验问题[J].南通大学学报：自然科学版，2013，12（ 1）：82-85.

[11]Rajan J， Jeurissen B， Verhoye M.Maximum likelihood estimation-based denoising of magnetic resonance images using restricted localneighborhoods [J].Physics in Medicine and Biology，2011，56（ 16）：134-139.

[12]Lui K J. A note on hypothesis test in binary data under the single-consent randomized design[J].Therapeutic Innovation&Regulatory Science，2006，40（ 2）：219-227.