改进EEMD高速列车隧道交会横向振动研究

何洪阳，陈春俊，孙 宇

（西南交通大学机械工程学院，四川 成都 610031）

0 引 言

随着列车的运行速度不断提高，空气动力效应加剧[1-2]，尤其当两列车在隧道交会时，产生的隧道交会压力波作用在会车侧表面，形成巨大冲击压力，对列车的车窗结构和强度以及稳定性带来很大影响[3]。列车线路运行时，其横向稳定性主要受轨道不平顺和气动载荷影响。目前，在轨道不平顺激励下，列车的横向振动及控制理论相对成熟[4]。气动载荷对列车横向振动的影响主要采用计算机数值建模仿真的方法进行研究[5]，但数值建模过程往往需对模型进行简化处理，其结果存在误差。

针对这一问题，提出一种改进的集合经验模态分解（IEEMD）方法对实测横向振动加速度进行经验模态分解，依据相关性系数重构气动载荷引起的横向振动基本模式分量（IMF），从而提取出气动载荷引起的横向振动，并验证结果的正确性。此外，对影响车体横向振动的因素进行分析，分别考虑轨道不平顺、气动载荷以及两者共同作用对列车横向振动的影响，为列车减振提供理论指导。

1 改进的EEMD算法

1.1 算法改进

经验模态分解（EMD）是Huang[6]首先提出的一种新型的时域分析方法，将复杂信号自适应地分解为有限IMF分量，反应信号内部的特征。但研究表明EMD对非平稳信号进行分析时，存在端点效应和模态混叠的问题。

EMD对非平稳信号进行分析时，在数据的两端会产生发散现象，并且这种发散现象会逐渐向内“污染”整个数据序列而使得分解结果严重失真，称为端点效应[7]。针对端点效应问题，国内外学者做了大量研究，总结为波形延拓法、数据预测延拓法、极值延拓法3类[8]。本文采用最小二乘支持向量机（LS-SVM）方法对端点进行预测延拓：将最小二乘线性系统作为损失函数，将不等式约束条件转化为等式约束；针对非线性样本数据，首先用非线性映射ψ（·）把样本从原空间映射到特征空间φ（xi），定义核函数为

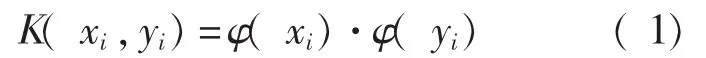
常用的核函数有多项式核函数、径向基核函数和Sigmoid核函数；同时将优化问题转化为求解线性方程，最后用最小二乘法求出a和b，得到非线性预测模型如下式所示：

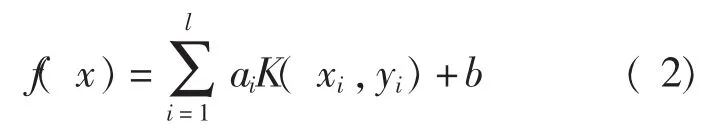
LS-SVM良好的回归预测性能对信号极值点幅值进行预测延拓，对给定的信号在端点处延拓有限个数据点，从而得到延拓序列。LS-SVM能抑制端点效应，但有待提高，其端点效应仍不确定，可能在两端造成发散现象，继续向内“污染”。目前已经提出了一些数据延拓与窗函数相结合的方法[9-10]，下面将LS-SVM和余弦窗函数结合，在保留波形延拓方法优势的基础上，通过加余弦窗函数，使端点为零，信号的包络线变得比较平滑，样条函数可以更好地拟合包络线，上下包络线收敛于端点，有效地消除端点效应。其表达式[11]如下：

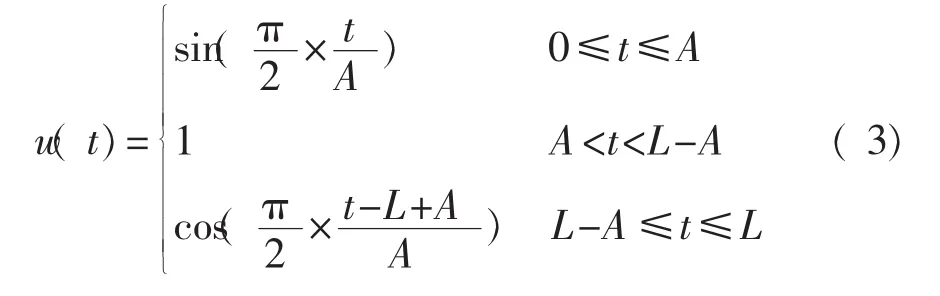
式中：L——信号延拓后的长度；

A——延拓信号的较长延拓长度，其余弦窗函数的形状如图1所示。

对信号进行EMD分解，将分解得出的IMF延拓部分去掉，从而抑制EMD端点效应。

同时，为抑制模态混叠，Wu等[12]提出了一种集合经验模态分解（EEMD）方法，该方法将噪声辅助分析应用于经验模式分解中以促进抗混分解，有效抑制了模式混叠现象。文献[13]在EEMD基础上提出了AEEMD，同时应用在转子油膜涡动的故障监测诊断中，提取出转子油膜涡动的故障特征，取得了很好的效果。使用EEMD进行经验模态分解时，需要设置两个参数，即加入原信号的噪声幅值k和执行EMD的总次数M，加入噪声对分解结果e的影响与k、M的关系式为

k越小、M越大，则e越小，但当k过小时，不足以引起信号局部极值点的变化，M过大将增加耗时，不利于实时分析。因此本文根据文献 [13]提出的EEMD加入白噪声的自适应准则，确定k和M值。

1.2 仿真实例分析

EEMD算法本质是EMD的改进，不仅具有EMD的优点而且还可以有效地抑制端点效应和模态混叠现象。为验证上述方法的有效性，仿真信号s由频率为10Hz正弦信号、Gauspuls脉冲分量以及趋势项组成，仿真原始信号s如图1所示。首先，利用LS-SVM对端点进行预测延拓；再将延拓信号s（t）与余弦窗函数进行内积运算；最后，对加窗后的仿真信号进行EEMD分解，根据自适应准则得到k=0.01，M=200，再将各IMF分量两端去掉相应的延拓部分。

对原始信号s进行EMD分解和改进的EEMD分解。图2为仿真信号的EMD分解结果，包括3个IMF分量和1个余项，显然，IMF1和IMF3完全失真，失去其物理意义；因此，直接对仿真信号进行EMD分解，存在严重的端点效应和模式混叠现象。图3为仿真信号用改进的EEMD分解结果，IMF1为Gauspuls脉冲分量，IMF3为正弦信号，res为趋势项，IMF2为脉冲信号和正弦信号的调制结果。

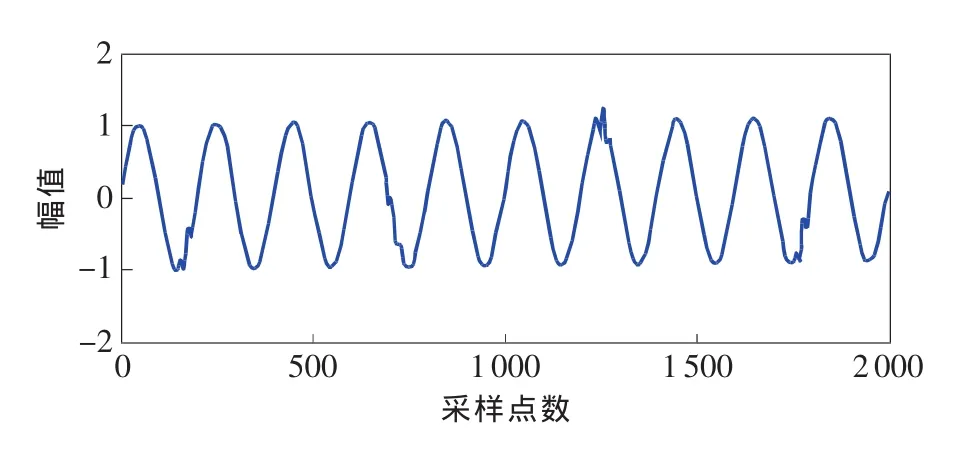
图1 仿真信号s

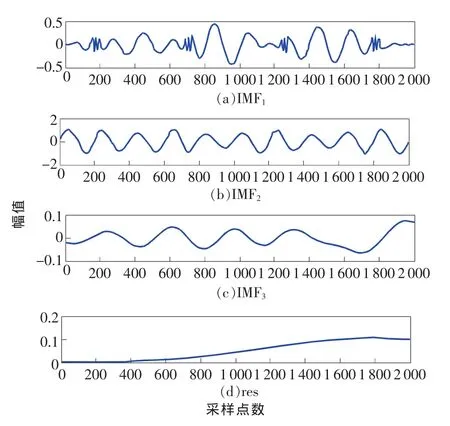
图2 EMD分解结果

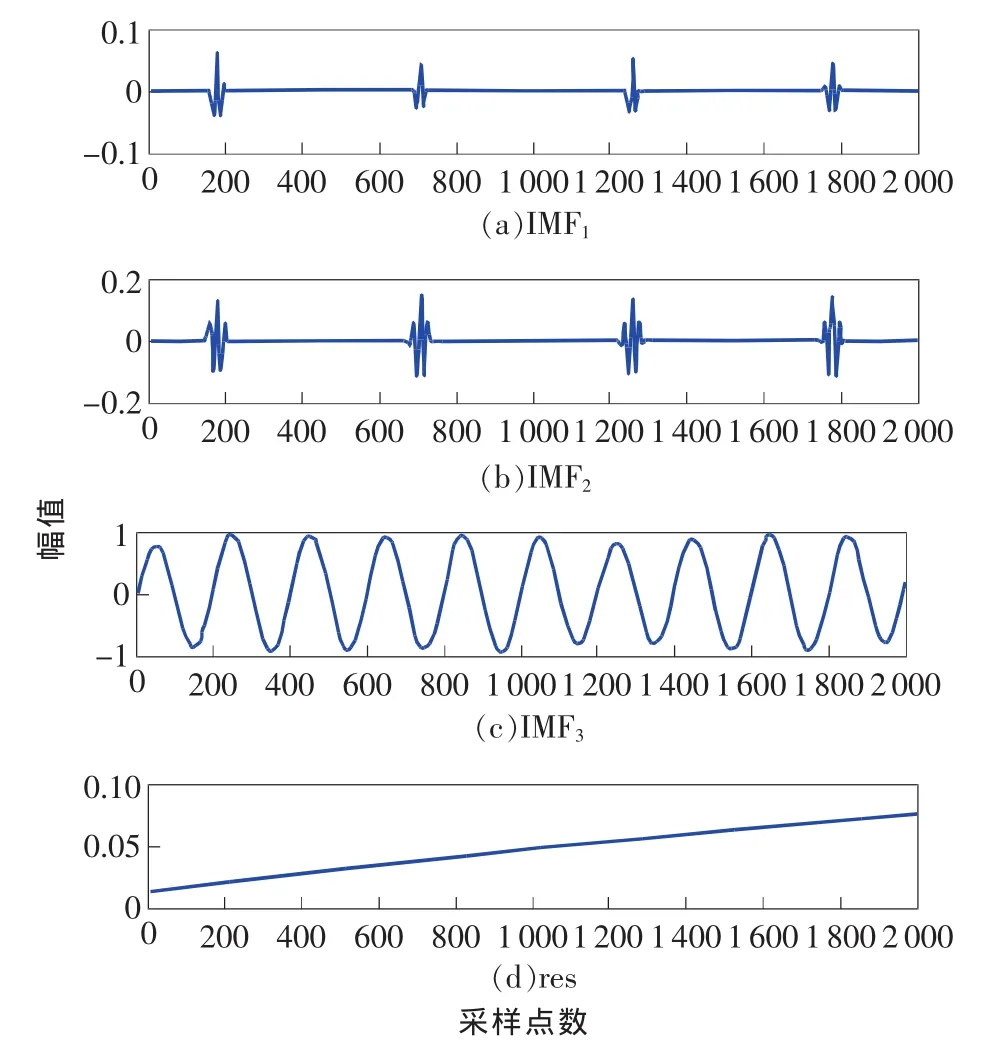
图3 改进的EEMD分解结果

2 气动载荷引起的横向振动提取

2.1 数据来源与试验方案

文中所用试验数据来自某CRH型高速列车（8编组列车）160km/h速度级的实测数据，其数据为尾车的会车侧车体表面压力信号和车体振动加速度信号，其中横向振动加速度为前后转向架心盘处左右各为1m处的值，系统的采样频率为2kHz。

列车以160km/h速度在某长300m隧道内进行交会，由于这是线路实际测试，其会车位置、两车相对速度以及是否同时进入隧道未知，但对本文的分析没有影响。图4所示为会车侧表面压力，从图中可知列车表面压力在隧道交会过程中波动较大，这是因为两列交会列车在隧道产生压缩波和膨胀波，并在隧道中再传播的过程中相互叠加。列车在1位置进入隧道，在2位置遇到膨胀波而压力下降，在3处遇到压缩波压力上升，两列车在4位置交会，隧道波与会车压力波叠加，在5位置列车驶离隧道。

图4 会车侧表面压力

图5 横向振动加速度

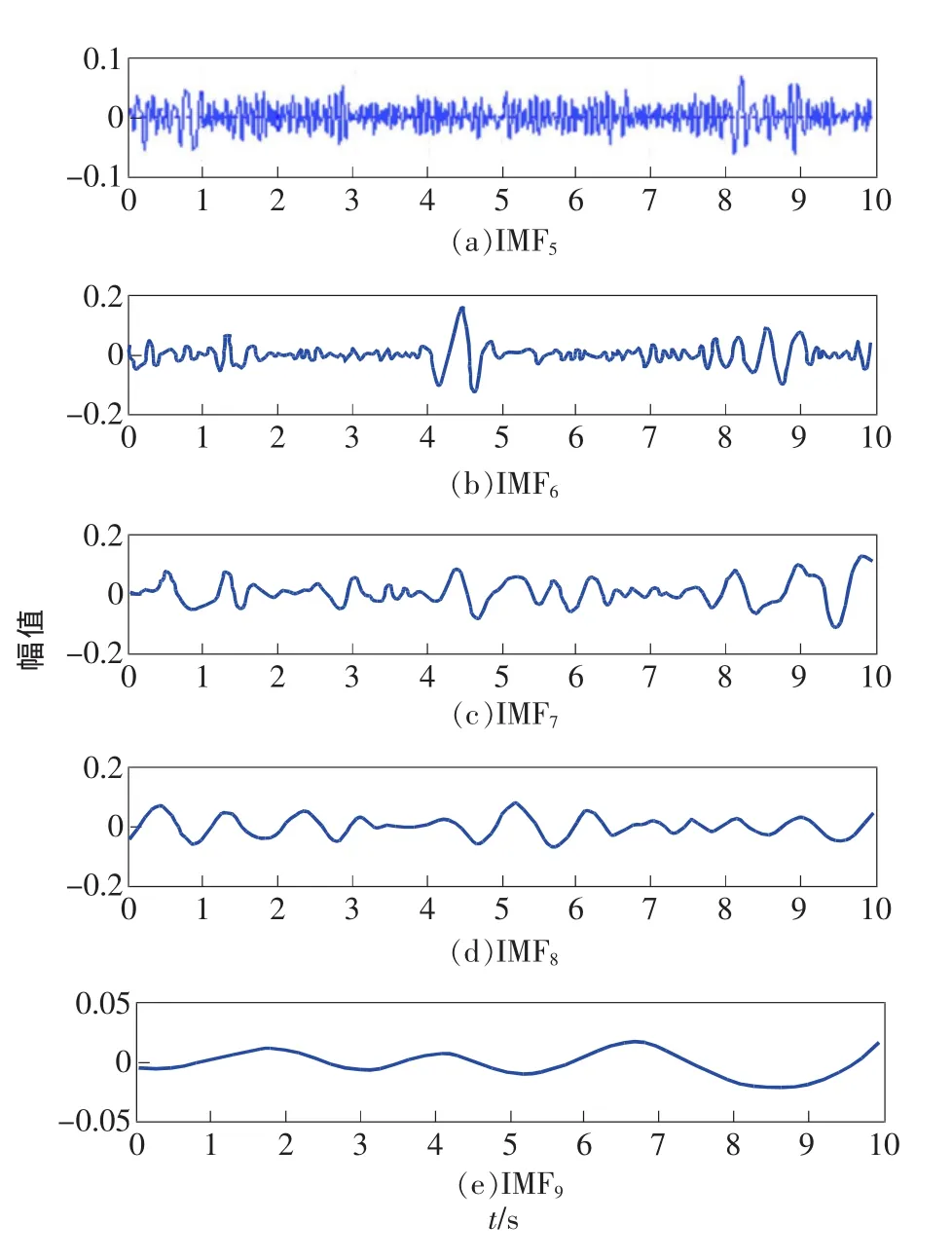
图6 横向振动IEEMD分解结果

正是由于在隧道交会过程中，列车表面产生复杂的压力波动，气动载荷对列车横向振动分析至关重要。图5为车体横向振动时域波形，在1时刻车头进入隧道，车尾振动较明显；在2时刻两列车在隧道中某位置交会，气动载荷作用使列车振动剧烈；在3时刻车尾离开隧道，振动也比较剧烈。由轨道不平顺引起的横向振动幅值在0.2m/s2附近，气动载荷和轨道不平顺共同作用下横向振动幅值在0.4m/s2左右。

2.2 基于IEEMD的横向振动提取

由图5可知，轨道不平顺引起的振动视为随机非平稳信号，气动载荷引起的振动视为Gauspuls脉冲信号；对上述横向振动加速度进行IEEMD分解，其IMF分量自适应地从原始信号中分解出来，分解为12层和余项。其中IMF5～IMF9分量如图6所示。

由分解结果可知，IMF6、IMF7、IMF8分量能很好地表征气动载荷引起的横向振动；同时，引入相关系数计算各IMF分量与原始信号的相关性[14]，其表达式如下式所示。相关性系数值越大表示相关性越好，反之越小。一般情况下，设置阈值ρ（j）为0.5，大于阈值的IMF分量视为有效分量，保留，小于阈值视为无效信号，剔除。

求出各IMF分量与原始信号的相关系数，如表1所示。 IMF6、IMF7和 IMF8的相关系数均＞0.5，认为是气动载荷引起的横向振动，并进行重构。气动载荷与轨道不平顺引起的横向振动时域波形如图7所示。由图可知，在进出隧道瞬间和刚会车时刻，气动载荷引起的列车横向振动明显加剧；而轨道不平顺引起的横向振动在整个过程比较平稳，幅值较小。

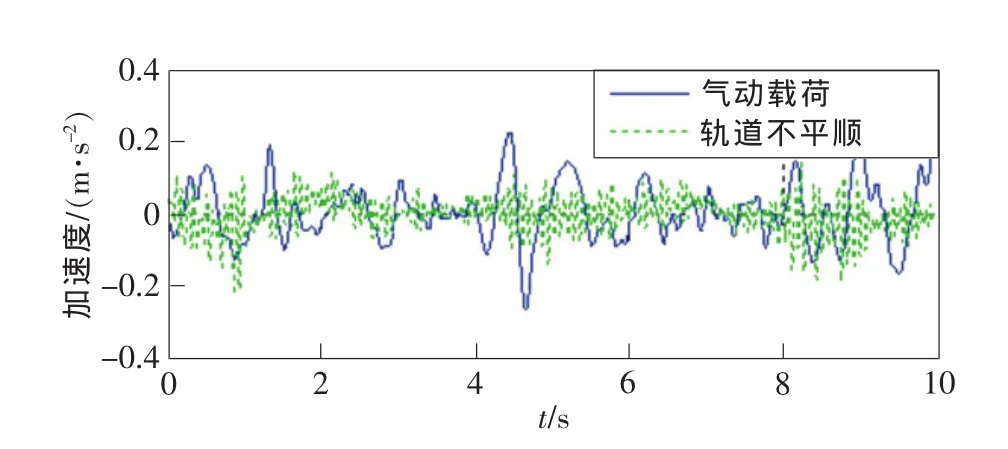
图7 横向振动时域图

表1 各IMF分量相关系数

2.3 结果验证

验证上述方法是否能有效提取气动载荷引起的横向振动加速度。取列车进隧道前的一段明线数据，横向振动加速度近似为由轨道不平顺引起，与图7虚线（绿色）所示的振动加速度进行比较，由于时域上存在相位差，故对其功率谱进行分析，其功率谱图如图8所示。由图可知，功率谱图在整个频段内基本重合，从而验证了上述提出方法的有效性。

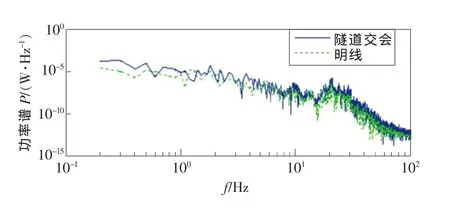
图8 轨道不平顺引起的横向振动PSD图

3 横向振动的影响因素分析

3.1 横向平稳性评定指标

平稳性是机车重要的动力学性能，也是评价车辆运行平稳性和旅客乘坐舒适性的重要指标。横向平稳性指标计算公式[15]为

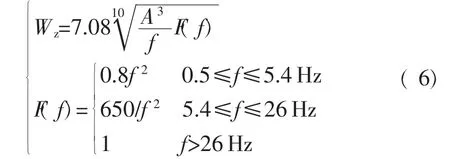
式中：Wz——横向平稳性指标；

A——车体振动加速度；

f——振动频率；

F（f）——频率修正系数。

根据最终频谱获得的A和f代入式（6）即可计算出车体的横向平稳性指标。

3.2 横向振动结果分析

列车以160 km/h速度在隧道内与另一列车交会，运用改进的EEMD方法提取出气动载荷引起的列车横向振动，并与轨道不平顺引起的横向振动进行比较，如图7所示。本文用加速度峰值、加速度均方根值和平稳性指标分别表述轨道不平顺、气动载荷以及它们共同作用引起的列车横向振动情况，具体如表2所示。由表可知，气动载荷引起的列车横向振动的均方根值、峰值以及平稳性指标均大于轨道不平顺引起的，其数值越大表示横向振动越剧烈，旅客乘坐舒适度越低。气动载荷引起的横向振动平稳性指标比轨道不平顺增大7.17%，轨道不平顺和气动载荷共同作用比仅轨道不平顺增大了13.02%。因此，由于轨道会车时气动载荷的作用，列车横向平稳性更加恶化，气动载荷是引起列车横向振动的主要原因。

表2 典型速度下横向振动评定指标

4 结束语

高速列车隧道交会时，产生的隧道交会压力波作用在会车侧表面，形成巨大冲击压力，引起列车横向振动加剧。同时，列车横向振动也受轨道不平顺影响。本文采用一种改进的EEMD方法对实测横向振动加速度信号进行改进的集合经验模态分解，并结合相关性系数，提取出隧道交会时气动载荷引起的横向振动。得出如下结论：

1）本文提出改进的EEMD方法能有效抑制端点效应和模态混叠现象，运用到高速列车隧道交会过程中，提取出气动载荷对列车的横向振动，取得了很好的效果。

2）列车隧道交会过程中，相比于轨道不平顺，气动载荷是引起横向振动的主要原因，尤其是两者共同作用下导致列车横向振动更加恶化。该结论为列车的减振提供理论指导。

[1]田红旗.列车空气动力学[M].北京：中国铁道出版社，2007：59-77.

[2]Raghu S， Kim H D， Setoguchi T.Aerodynamics of high-speed railway train[J].Progress in Aerospace Science，2002（ 38）：469-514.

[3]田红旗，姚松，姚曙光.列车交会压力波对车体和侧窗的影响[J].中国铁道科学，2000，21（ 4）：8-14.

[4]陈春俊.高速列车横向主动/半主动悬挂控制研究[D].成都：西南交通大学，2006.

[5]李雪冰，侯传伦，张曙光，等.高速列车交会时的风致振动研究[J].振动与冲击，2009，28（ 4）：81-88.

[6]Huang N E.The empirical model decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proc R Soc Lond，1998（ 454）：903-995.

[7]陈双喜，林建辉，陈建政.基于改进的EMD方法提取车辆-轨道垂向耦合系统动态特性[J].振动与冲击，2011，30（ 8）：213-216.

[8]郭明威，倪世红，朱家海，等.振动信号中HHT/EMD端点延拓方法研究[J].振动与冲击，2012，31（ 8）：62-65.

[9]李敏，程珩，张斌.EMD端点效应处理方法研究[J].太原理工大学学报，2009，40（ 6）：579-581.

[10]旷欢，王如龙，张锦，等.基于SVM的EMD端点效应抑制方法研究[J].计算机工程与应用，2015，51（ 11）：196-200.

[11]时培明，丁雪娟，李庚，等.一种EMD改进方法及其在旋转机械故障诊断中的应用[J].振动与冲击，2013，32（4）：186-188.

[12]Wu Z H，Huang N E.Ensemble empirical mode decomposition:a noise assisted data analysis method[J].Advances in Adaptive Data Analysis，2009，1（ 1）：1-41.

[13]蔡艳平，李艾华，徐斌，等.集成经验模态分解中加入白噪声的自适应准则[J].振动、测试与诊断，2011，31（ 6）：709-713.

[14]丁常富，蔡志成.EMD中有效IMF选取方法的研究[J].热力发电，2014，43（ 1）：36-39.

[15]任尊松.车辆动力学基础[M].北京：中国铁道出版社，2007：135-152.