基于离散椭球基-基扩展模型的OFDM信道估计



基于离散椭球基-基扩展模型的OFDM信道估计

孙增友,李欢欢,凌 霞

(东北电力大学信息工程学院,吉林吉林132012)

摘 要:为准确掌握信道特性,提出了基于离散椭球基—基扩展模型(Discrete Prolate Spheroidal Sequences-Basis Expansion Model,DPSS-BEM)的OFDM信道估计方法。采用二维DPSS-BEM对信道进行建模,将信道视为二维正交分量的线性加权,并利用导频位置的训练信息估计权值。仿真表明,该方法与基于极值BEM算法、卡尔曼估计法比较,能有效跟踪OFDM信道变化,改善信道的归一化均方误差和误码率性能。

关键词:正交频分复用;导频;信道估计

OFDM(正交频分复用,Orthogonal Frequency Division Multiplexing)系统中信道估计是决定系统能否正常工作的关键技术之一。而在高机动收发设备及高载频上实现宽带数据通信时,信道将发生快速时变。即使在一个OFDM符号时间内,信道也是变化的,此时,OFDM系统将无法应对快速时变信道产生的ICI(信道间干扰,Inter-Carrier Interference)。用常规信道估计方法对信道进行估计时,建模误差会增加,估计性也将能下降。为此,有必要研究信道估计技术,对信道进行有效跟踪和补偿,确保OFDM子载波间的正交性,提高载波通信性能[1]。目前,利用导频OFDM信道估计,是针对信道在一定时间内保持不变的情况,无法适应复杂多变信道,且信道的未知参数常大于能提供的训练序列或导频符号的个数,无法直接估计信道。近年来提出的采用建立模型的方法对信道进行逼近,以减少待估计参数个数的信道估计方法,当信道快速变化时,建模误差会增加,估计性能下降[2]。基于DPSS-BEM的OFDM信道估计方法,将信道视为二维正交分量的线性加权,并利用导频位置的训练信息估计权值,从而得到更接近实际的信道参数。

1　OFDM系统模型

OFDM系统时域不加循环前缀时接收符号的表达式为

式(1)中x(t,n)(k)表示传输的第n个OFDM符号,k = (0,…,N - 1),l = (0,…,L - 1),L =「τmax/ Tsamp⌉,是基带信道冲击响应(Channel Impulse Response,CIR)持续的长度,τmax为最大时延,Tsamp为采样周期。h(n)(k,l)是第n个符号在k时刻的CIR;ω(t,n)(k)是均值为0,方差为σ2ω= N0/2复加性高斯白噪声。式(1)的矩阵形式为

对应频域表达式为

其中,ω(n)是频域噪声。由F-1= FH和FHF = I,I是N×N的单位矩阵,

其中,H(n)= Fh(n)FH,是信道频率矩阵(CFM,Channel Frequency Matrix)。当时频选择性频移可以忽略时,H(n)是对角阵,系统无ICI。对于快时变信道,H(n)是带状的,从而存在ICI。

2　信道估计算法

采用DPSS - BEM建模和DPSS - BEM基系数内插的方法来进行信道估计,信道视为二维正交分量的线性加权,用两组DPSS基,分别作为时频域基函数。利用时变信道的窄带特性,将时变信道转化为少量正交分量的线性加权,而DPSS - BEM基系数为正交分量的权值[3]。

2.1 二维DPSS - BEM

将时变CIR建模为二维基函数的线性加权,

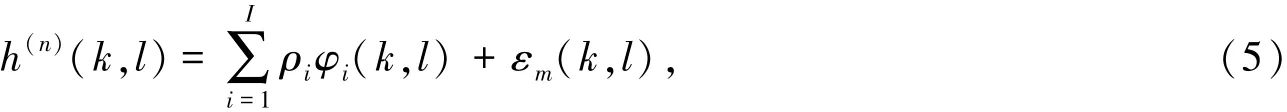
其中,ρi是单符号内时变信道基函数φi(k,l)的权值,I(0 < I < N2)是基函数个数,εm为建模误差。二维基函数可分解为时频域一维基函数的乘积[4],

其中,i = q + Q(r - 1),(1≤r≤R,1≤q≤Q)。R和Q分别指时域基函数υr(k)和频域基函数γq(l)个数。由于离散长球序列(DPSS,Discrete Prolate Spheroidal Sequences)在有限时间或有限带宽内集中了大部分能量,仅需最长时间T或最大带宽Bω进行计算[5]。

由DPSS函数的特点可知,在频域和时域中所需基函数个数R可由「BωT⌉+ 1得出[6],则

式中,B为有效带宽,τmax为最大信道时延。

式中,vmax为最大时频选择性频移,Ts为OFDM符号周期。

2.2 权值估计

权值估计由当前OFDM符号和Ns个前后毗邻符号中导频处的训练信息来完成。Ns由下式给出。

式中,NR为前毗邻符号数,NL为后毗邻符号数,将要进行CFM估计的符号为当前符号。基函数个数为

2. 2. 1 当前OFDM符号

OFDM系统时域接收符号

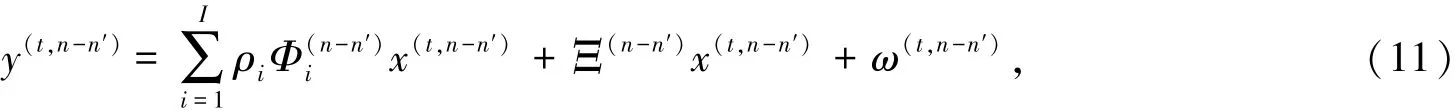
其中,n′= (NL,NL- 1,…,0,…, - NR+ 1, - NR),Ξ(n)为建模误差矩阵,

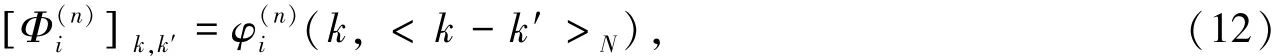
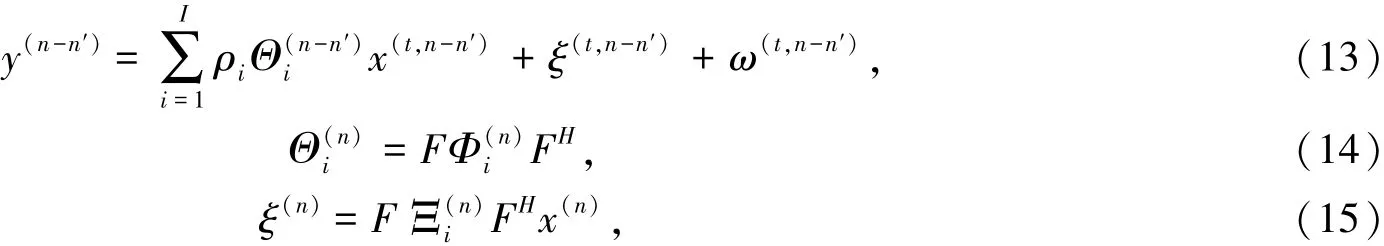
对应频域表达式为式中,ξ(n)为由建模误差引起的ICI。

2. 2. 2 导频处训练信息

设x(pn)和y(pn)为在导频处大小为Np的矢量,元素分别为x(n)和y(n)。Θni,p是相应导频处,由Θ(in)中元素形成的大小为NP×NP的子矩阵。通过对式(11)进行采样,导频处接收信号为

上式中,ϑ(n-n′)为数据子载波在导频处产生的ICI,ξ(pn-n′)和ω(n-n′)分别为ξ(pn-n′)和ω(n-n′)在导频处的采样。x(pn)和Θ(i,np)是接收机预先知道的,它们的乘积Λ(n)可以预先存储和计算,

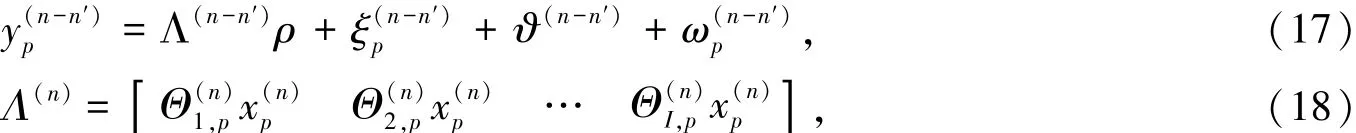
Λ(n)大小为ρ=[ρ1ρ2…ρI]T为待估计权值向量。接收符号可表示为

矢量ιp是数据子载波引起的ICI、建模误差和加性噪声等零均值不相关随机变量的线性组合。由中心极限定理知,ιp中的元素是零均值高斯变量。则权值估计可以通过最小均方(LS,Least Square)算法实现[7],

其中,ρ^是权值估计量,Γ= (ΛHΛ)-1ΛH。

3　OFDM信道仿真

基于DPSS - BEM算法的OFDM信道估计分析从信道的归一化均方误差和误码率性能两方面进行仿真。系统参数为数据星座为4 QAM,90个子载波作为保护频带。归一化频移为fd= 0. 1,0. 2,用误比特率(bit error rate, BER)和归一化均方误差(normalized mean square error,NMSE)进行性能分析。

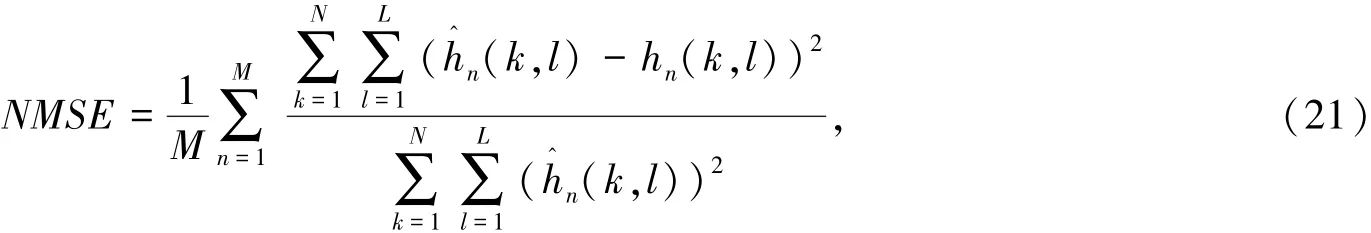
式中:M是传输符号数。仿真中,时频域基函数个数分别由式(6)和式(10)计算得到Q = 26,Rext= 3,仿真结果见图1 - 4。

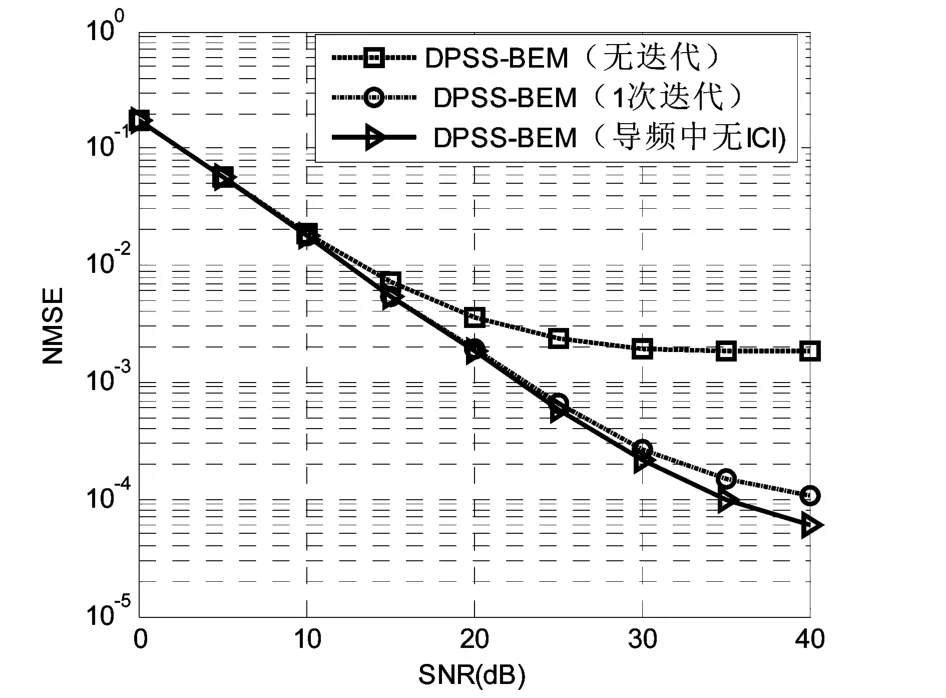
图1　3种DPSS BEM的NMSE性能

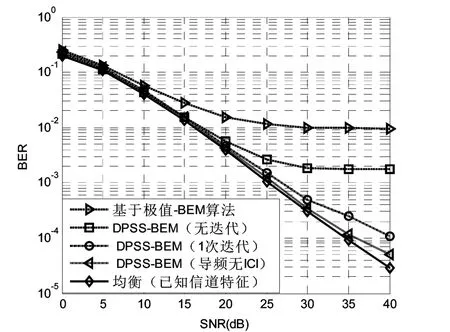
图2　DPSS BEM、极值BEM的BER性能

图1为DPSS-BEM算法在无迭代、1次迭代、导频中无ICI三种情况下的NMSE性能,fd=0. 1。仿真结果表明采用迭代方案时性能优于无迭代方案的性能,且优势随SNR增大而增大。1次迭代足以消除数据符号在导频处引起的ICI,信道估计精确度提高。

图2为在无迭代、1次迭代、导频中无ICI三种情况下的DPSS-BEM算法与基于极值BEM算法[8]的BER性能。已知信道状态信息下,将均衡后的性能作为参考,为最佳可实现的BER性能。仿真结果表明在SNR>10 dB时,基于极值的BEM算法性能,要远低于DPSS-BEM。DPSS-BEM在导频中无ICI 时,性能接近最佳性能。且经迭代运算后,算法性能接近DPSS BEM在导频中无ICI时的性能。当SNR ≤20 dB时,三种DPSS-BEM的性能与最佳性能均一致。随着SNR的增加,较无迭代情况,迭代后的性能显著提高,当SNR=40 dB时,性能优势达到10倍。说明消除数据符号在导频处产生的ICI,能进一步提高信道估计的BER性能。

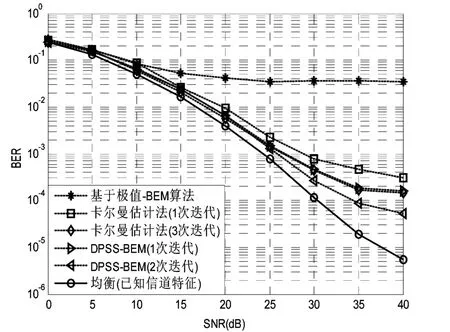
图3　信道估计算法的BER性能比较

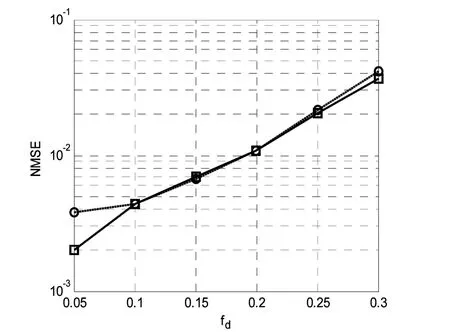
图4　在不同的fd下,DPSS BEM的NMSE性能

本文提出基于DPSS-BEM的时OFDM信道的信道估计方法,使用迭代方案消除数据中的ICI对导频子载波的干扰,进一步提高了信道估计的性能。且仅需要最大时延、最大时频选择性频移、有效带宽和符号周期这些先验信息即可,仿真结果表明,此估计算法对快速时变OFDM信道有较好的估计效果。

参 考 文 献

[1] 张勤进,刘彦呈,赵又涛,等.低压电力线信道的决策估计算法研究[J].电力系统通信,2011,32(3):5-9.

[2] HRYCAK T,DAS S,MATZ G,et al. Practical estimation of rapidly varying channels for OFDM systems[J]. IEEE Trans. Commun. ,2011,59

图3为基于极值BEM算法、卡尔曼估计法[9](1次迭代)、卡尔曼估计法[10](3次迭代)DPSS-BEM (1次迭代)、DPSS-BEM(2次迭代)和已知信道状态信息下,进行均衡后的BER性能比较图。fd=0. 2, 当SNR<20 dB时,所有算法的性能接近最佳性能。当SNR>20 dB时,DPSS-BEM(1次迭代)与卡尔曼估计法(3次迭代)的性能相近,比基于极值的BEM算法的性能好。DPSS-BEM(2次迭代)算法比卡尔曼估计法(3次迭代)性能好,在SNR=40 dB时,DPSS-BEM(2次迭代)的BER低于10-4,而卡尔曼估计法(3次迭代)的BER高于10-4。由图1和图2知,随着fd的增大,迭代次数相应增加,DPSS-BEM才能获得最好的估计性能。

图4为DPSS-BEM在不同的fd下的NMSE性能。实线表示I由对应的fd确定时,DPSS-BEM算法性能,虚线为I由fd=0. 2时,DPSS-BEM算法性能。仿真结果表明两种情况下NMSE性能相当,说明此算法具有一定的鲁棒性。

4　结 语

(11):3040-3048.

[3] 李丹,柯峰.一种基于基扩展模型的OFDM频域快时变信道估计方法[J].信号处理,2012,28(2):193-199.

[4] 吴君钦,赵雪. LTE下行基于时频二维信道估计算法性能分析[J].计算机工程与设计,2013,34(4):1162-1166,1176.

[5] LONGORIA-GANDARA O,PARRA-MICHEL R. Estimation of correlated MIMO channels using partial channel state information and DPSS [J]. IEEE Trans. Wireless Commun. ,2011,10(11):3711-3719.

[6] ZEMEN T,BERNADO L,CZINK N,et al. Iterative timevariant channel estimation for 802.11p using generalized discrete prolate spheroidal sequences[J]. IEEE Trans. Veh. Technol. ,2012,61(3):1222-1233.

[7] 赵旺兴,万群,陈章鑫.基于OFDM循环前缀LS信道估计的构造方法[J].通信学报,2013,34(3):175-182-191.

[8] 温亚萍,张冀.基于BEM的时变信道估计改进算法[J].无线通信技术,2014,40(1):48-50.

[9] 叶磊.基于卡尔曼滤波的OFDM系统时变信道估计方法[J].微型机与应用,2013,32(6):56-60.

[10]隋吉生,赵亮,王圣达,等.基于MMSE的无线OFDM系统信道估计算法[J].东北电力大学学报,2014,34(6):77-79.

OFDM Channel Estimation Based on Discrete Prolate Spheroidal Sequences-Basis Expansion Model

SUN Zeng-you,LI Huan-huan,LING Xia

(School of Information Engineering,Northeast Dianli University,Jilin Jilin 132012)

Abstract:To master the channel characteristics,broadband power line carrier OFDM channel estimation based on DPSS-BEM is proposed,which models power line channel by using two-dimensional DPSS-BEM to regard the power line channel as linear weighting of two-dimensional orthogonal components,then treated the channel variation during OFDM symbol as the variety of weights,and then utilized the training information from pilots method to estimate weights to complete channel estimation. The simulation results show that the method can effectively track the changes of power line channel,obviously improve the normalized mean square error and bit error rate performance.

Key words:OFDM;Pilots;Channel estimation

作者简介:孙增友(1963-),男,吉林省镇赉县人,东北电力大学信息工程学院高级工程师,主要研究方向:无线通信、电力系统通信.

收稿日期:2014-11-25

文章编号:1005-2992(2015)02-0089-05

文献标识码:A

中图分类号:TM73