基于压缩感知的OFDM稀疏信道估计中的导频设计*
2022-03-03
(重庆理工大学 电气与电子工程学院,重庆400054)
0 引 言
在正交频分复用系统中,相干检测要求精确的信道估计。传统的信道估计需要大于信道长度的导频数去恢复完整的信道估计,并没有考虑多径无线信道的特性。事实上,在信道时延扩展中,大多数信道脉冲响应系数为零或近乎为零,即宽带无线信道一般呈现稀疏结构[1-2]。近年来,压缩感知(Compressed Sensing,CS)技术在信道估计的应用引起了许多学者的关注,稀疏信道估计可以表述为稀疏恢复问题,在接收端仅用较少的测量值就能够恢复原始信号。与传统的最小二乘(Least Square,LS)法和最小均方误差(Minimum Mean Square Error,MMSE)法相比,基于CS的导频辅助信道估计能够呈现更好的信道估计质量,且能够有效节省导频数量,其中导频图案设计是信道估计中的关键难题之一。
传统导频图案都是要求导频等间隔放置才能够获得最优信道估计效果,但在基于CS的导频辅助信道估计中,同样的导频放置方法并不适用。文献[3]从实现最小测量矩阵互相关值的意义上证明,只有基于循环差集(Cyclic Difference Set,CDS)的导频设计才是最优的。对于循环差集不满足的情况下,提出了许多方案去寻找接近最优的导频图案。文献[4]将矩阵互相关定义为采样矩阵中的任意两列之间最大内积值,通过随机导频搜索算法生成一定数量的导频组,计算每组导频中的最大互相关值,从中挑选最小的一组作为最优导频。虽然该算法复杂度较低,但算法精度取决于随机次数及随机概率。文献[5]提出一种基于导频位置差异方差最小化(Positions Differences Occurrences,PDO)的贪婪算法来寻找合适的导频索引集。文献[6]提出双循环导频搜索算法,每一次外循环导频都作为内循环的初始导频,通过设置内外循环次数可以灵活控制算法的精度与时长,但该算法还是属于贪婪算法,每次循环都是独立进行,算法效率并不高效,可能存在局部最优的情况,估计效果不够理想。文献[7]采用基于树的反向迭代算法搜索导频位置,保留每次迭代中最小互相关值的导频,但该迭代树并不是完备树,也可能存在收敛到局部最优的情况。
本文提出一种新的采样矩阵互相关评价准则并将使用该准则的导频图案应用于信道估计;同时,通过分析相邻导频之间的间隔大小关系,提出一种新的高效导频搜索算法,能够快速收敛到较小的互相关值。从仿真结果看,对比现有互相关准则及导频搜索算法,本文新提出的准则和算法具有一定的优势。
1 基于CS的信道估计模型
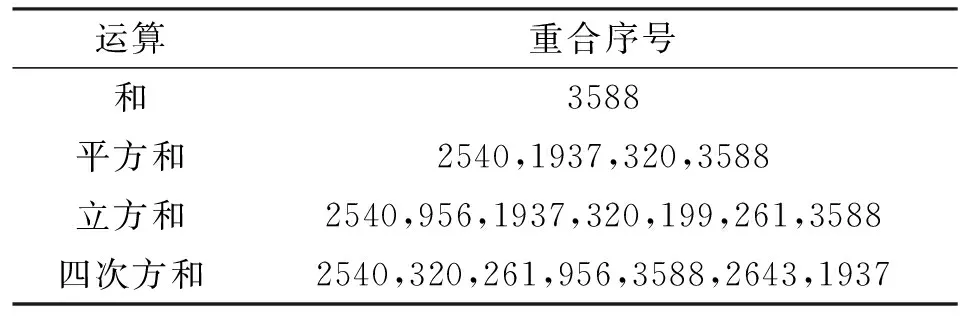
假设一个包含N个子载波的正交频分复用系统,令其中Np个作为导频子载波,p1,p2,…,pNp表示导频位置,规定1≤p1 yP=XPWPh+nP=Ah+nP。 (1) 式中:yP=Sy是P×1维向量,接收信号y=[y(0),y(1),…,y(N-1)]T;XP=SXST是P×P对角矩阵;WP=SW是P×L矩阵;h=[h0,h1,…,hL-1]T为信道的时域冲激响应采样值;nP=Sn是P×1维噪声向量;A=XPWP是P×L维测量矩阵;S矩阵由N×N维单位矩阵中与导频位置对应的P行组成,[η(1),η(2),…,η(Np)]T~CN(0,σ2INp)满足独立同分布的高斯白噪声;WNp×L为从一个矩阵维度为N×N的离散傅里叶变换(Discrete Fourier Transform,DFT)矩阵中挑选Np个导频所在的行和前L列所构成的部分DFT矩阵, (2) 传统的LS信道估计问题针对的是采样矩阵A中行数大于列数的情况,即Np≥L。通常情况下,无线信道中的大部分能量仅分布在少量抽头上,因此可认为信道h具有稀疏结构。此时,再用LS信道估计不能很好估计信道质量,故可通过压缩感知理论去解决稀疏信号问题,利用少量导频即可恢复原始信号,即Np 由压缩感知理论可得,在没有噪声的情况下,若想通过测量值y和采样矩阵A以很高概率恢复h,则矩阵A必须满足有限等距性质(Restricted Isometry Property,RIP)[8],即 (3) 式中:常数δs∈(0,1)。 然而,验证矩阵A是否满足RIP特性是个NP-难问题,目前还没有一种公认确定的办法能够在多项式时间内得出结论,因此可以比较矩阵列之间的互相关准则来代替RIP。文献[9]证明采样矩阵互相关准则强于RIP,互相关值越小稀疏重构的概率就越高。 采样矩阵互相关定义如下: (4) 式中:〈·,·〉为内积;A(i)代表采样矩阵A的第i列。 倘若Np个导频功率相同,即 |x(p1)|2=|x(p2)|2=…=|x(pNp)|2, (5) 将式(2)代入式(4)中,可得 (6) 对矩阵A每个列向量进行归一化,并令G=abs(AHA),可得G是一个对称矩阵,其对角线元素gij,i=j为1,非对角线元素gij代表矩阵A中的第i列和第j列的互相关值大小。因此,式(6)又可表示为 (7) 由式(6)可以看出,导频分布P=[p1,p2,…,pNp]决定了最大互相关值μ(A)的大小。因此,导频图案设计就是寻找合适的Np个导频位置使得μ(A)足够小,即 (8) 文献[3]指出采用较小μ(A)值的导频图案不一定能有更好的估计效果,从互相关定义上看,该准则只能反映测量矩阵两列间的局部相关性,并不能很好体现所有列之间的全局相关性。文献[10]认为任意两列之间相关性为零的采样矩阵才是最优的,即矩阵G越接近单位矩阵,评价性能越准确。 γ(A)=‖G-I‖2。 (9) 然而,根据循环差集设计的理想矩阵并不是单位矩阵,而是矩阵中每个非对角线元素接近于零且大小相等,因此该准则不能很好评价采样矩阵的恢复性能。文献[11]仅考虑G中相关值较大的元素,选取t=0.15作为阈值,将超过阈值的元素三次方和作为矩阵的评价准则。 (10) 该方法虽简化了采样矩阵整体相关性,但并没有包含所有的元素,不能够完全正确有效地评价整体相关性好坏。另外,文献[11]只针对N=512、Np=24、L=50的特殊情况,并没有一定的普适性。因此,如何定义合适的导频设计准则去准确评价采样矩阵的重建性能仍是一个有待研究的问题。 通常情况下,好的信道估计要求采样矩阵A各列之间相关性越小越好,且较大互相关值个数越少越好,尽可能满足G中各个非对角线元素较小且相等。若G中除最小元素外的每个元素与最小元素的距离越近,就说明A中各列之间的相关程度就越小。因此,本文提出一种新的导频图案准则,即最小互相关距离立方和准则。 首先搜寻G中最小元素的值: (11) 接着,计算剩余每个元素与该最小元素的距离立方和。因为G为一个对称矩阵,且对角线上元素均为1,故可仅考虑G下三角元素。 (12) 式中:c=k-l,k、l分别代表为G的第k行和第l列。 导频图案设计问题可以转化为求解以下最优化问题: (13) 从式(12)可以看出,求解式(13)仅与导频位置索引集合Popt有关。而在N个空闲位置选择P个确定位置是个组合优化问题,且子载波数量远远大于导频数,即N≫P,故穷尽所有可能导频位置去选择最优位置解是不切实际的,可通过导频搜索算法寻找次优解,尽可能地接近最优解。 现有导频搜索算法都从导频位置考虑。文献[10]采用基于并行树的循序替换导频位置搜索算法,即在每一个导频位置上都循环遍历所有可能取值,并分别计算其互相关值,若子载波数量N较大,将会造成导频搜索时长过长。 由文献[4]附录可得,适当的导频间隔能拥有较好的互相关值,过大或过小的导频间隔都会影响估计质量。根据2.2节提出的新导频图案设计准则,本文从导频间隔角度考虑导频图案位置,提出一种新的导频搜索算法,即基于树的顺序替换导频间隔搜索算法。算法具体步骤如下: 初始化:设树的数量为Ntree=M1,存活分枝数量为Nsuv=M2;导频数量Np,OFDM子载波数目N,根节点号l=1。 Step1 根节点号为l,从N个子载波中随机挑选Np个位置,得到一组导频图案P作为初始导频图案。 Step3 选择存活分枝。根据式(12)计算所有新生成导频图案对应的ξ值,升序排列所有ξ值,选择前M2个导频图案PM2作为下一次替换父节点。令存活分枝序号j=1,m=m+1。 Step5 判断是否替换完所有存活分枝。若j满足为M2,则一共至多可以产生M2×((a+70)-(a+5)+1)个新的导频图案,并继续执行Step 6;若不满足,则使得j=j+1,并返回Step 4。 Step6 根据式(12)计算新的M2×((a+70)-(a+5)+1)个导频图案对应的ξ值,升序排列所有ξ值,选择前M2个导频图案PM2作为下一个位置替换父节点。 Step7 判断是否替换完所有导频位置。若m满足为Np,则记录当前最小ξ值及其对应的导频图案Pl,并继续执行Step 8;若不满足,则使j=1,m=m+1并返回Step 4继续循环。 Step8 判断是否循环完所有树。若l满足为M1,则继续执行Step 9;若不满足,则执行l=l+1并返回Step 1。 Step9 输出结果。从M1个可选图案P1,P2,…,PM1中选择最小ξ值对应的导频图案Popt作为最优导频图案。 图1 二分支树结构 图2 不同导频设计中的误码率 图3 不同导频设计中的均方误差 由仿真结果可得,在导频数较少的条件下,通过传统的LS算法恢复得到的信道估计远远不如基于压缩感知的信道估计;在基于压缩感知的信道估计中,等间隔均匀导频并不是最优的,传统导频搜索算法与文献[6]提出的SSS算法均采用采样矩阵最小互相关准则,通过该准则选取出来的导频位置能够比均匀导频更好地估计出真实信道;与采样矩阵最小互相关准则相比,采用新准则设计出的导频图案信道估计均方误差更低,在相同的误码率情况下最多能够节省约4 dB信噪比,与基于压缩感知的均匀导频信道估计相比信道估计均方误差减小约16 dB;与文献[10]提出的算法相比,本文算法误码率和均方误差曲线均略低于文献[10]算法,然而两者性能相差很小,算法曲线近乎一致,最大仅有约0.1 dB性能差距。在复杂度方面,本文算法的计算复杂度更低,算法效率上具有相对优势。仿真结果表明,与其他采样矩阵评价准则相比,本文提出的最小互相关距离立方和准则能够得到更优的信道估计质量。 为了比较不同导频搜索算法之间的性能差异,本节从ξ值优化结果和导频优化效率两个方面分析评价。由于考虑到实验结果会受循环次数的影响,外循环次数设置为1,初始导频均为[14,16,21,23,77,84,122,126,170,172,174,175,176,191,221,224,282,366,373,386,423,426,432,436],待替换导频个数为24个。从图4可以看出,两种导频搜索算法在前一半导频位置时ξ值收敛速度较快;随着导频不断替换更新,在后一半导频位置中ξ值收敛速度逐渐放缓。从第8个导频位置处开始,本文提出的新算法仍能保持较大的收敛趋势,与文献[6]提出的SSS算法相比,能够找到更小的ξ值。 图4 不同导频搜索算法中ξ值的下降曲线 导频搜索效率关键在于导频搜索算法时长,每一个待替换导频都需计算一次ξ值。为了保证算法公平,SSS算法外循环次数和TSS算法树个数均为M1,SSS算法内循环次数和TSS算法存活分枝个数均为M2。不同算法优化后的ξ值及运行时长如表1所示。从表1可得,与SSS算法相比,本文算法的收敛速度更快,且能获得更小的ξ值。综合导频优化效率和ξ值优化结果,本算法具有更优的导频搜索能力。 表1 不同算法优化后的ξ值及运行时长 为了确定哪种运算更加符合导频准则,利用5 000组不同导频集合仿真获得在不同信噪比条件下的MSE,并对每个导频在5 dB到20 dB内的所有MSE取平均。将5 000组不同导频集合对应的最小平均MSE按顺序排序,选择前10个导频集合,其对应序号分别为2540,956,1937,979,320,199,261,3588,2643,1233。同时将这5 000组导频集合分别采用和、平方和、立方和与四次方和运算进行计算,顺序排列所有互相关值,取前10个最小互相关值的序号,将这些序号与最小平均MSE序号相一致的序号列在表2中。从表2可以得出,立方和与四次方和都能够与最小平均MSE序号保持较好的一致性,而在复杂度上,四次方和的计算量较大,因此选择立方和作为准则较为合适。 表2 不同运算与具有最小平均MSE相重合的序号 本文针对基于CS的OFDM稀疏信道估计中的导频设计问题,提出新的采样矩阵互相关定义和导频设计准则。不同于传统互相关准则,该准则能够更好地反映采样矩阵全局相关性。同时,本文在基于树的循序导频位置搜索算法的基础上,考虑了相邻导频之间的间隔关系,提出一种新的基于树的顺序替换导频间隔搜索算法。仿真结果表明,本文算法能够在较短的时间内快速收敛到更小的互相关值,通过该算法所搜索得到的导频应用于信道估计中具有更小的误码率和均方误差。 本文的采样矩阵是傅里叶采样矩阵,下一步将研究高斯矩阵、伯努利矩阵等作为采样矩阵时如何准确评价采样矩阵的重建性能的问题。
2 导频设计准则
2.1 传统的最小互相关准则

2.2 新的导频图案设计准则

3 基于树的顺序替换导频间隔搜索算法
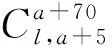

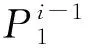

4 仿真分析
4.1 均方误差和误码率比较
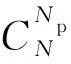
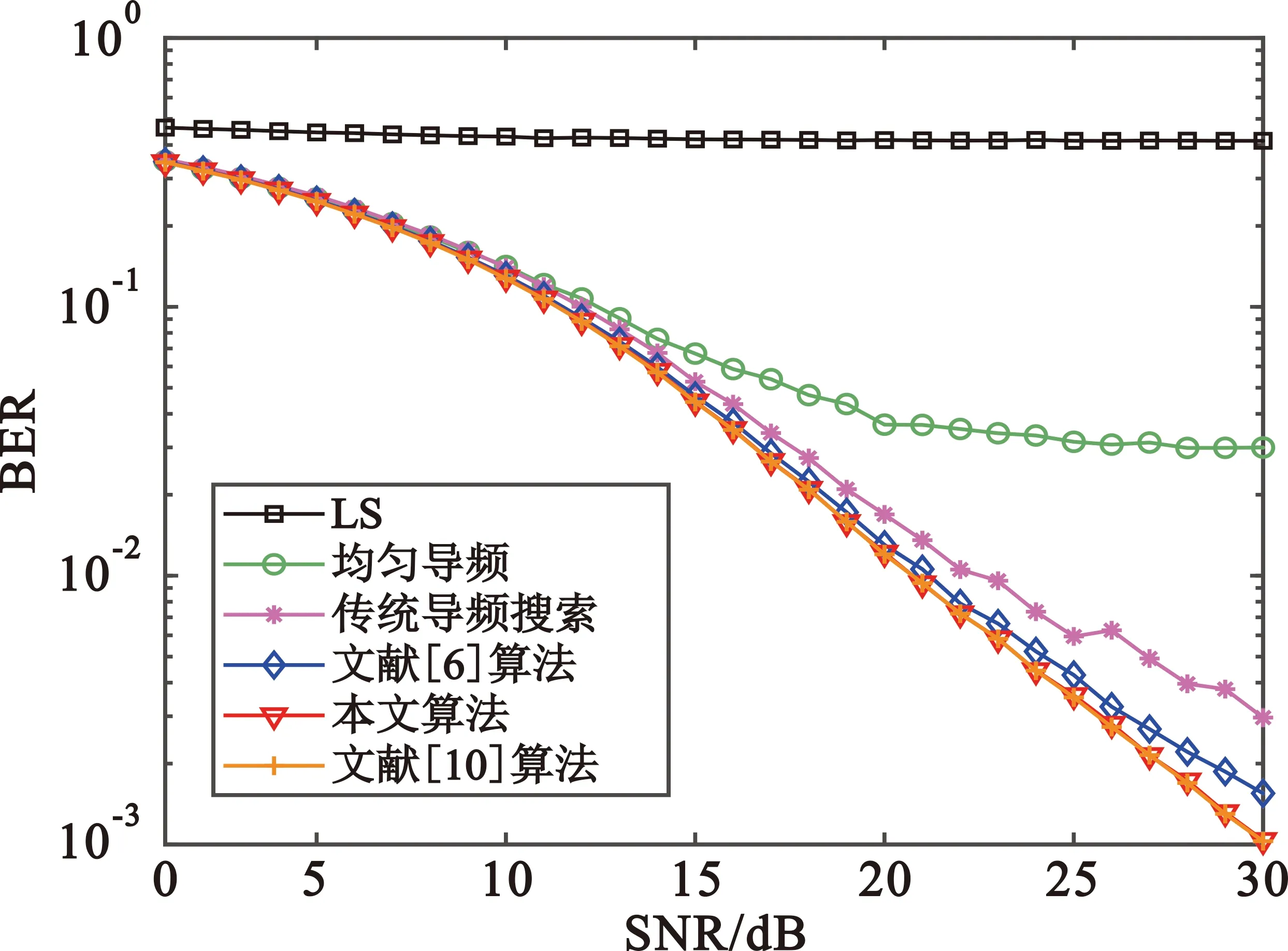
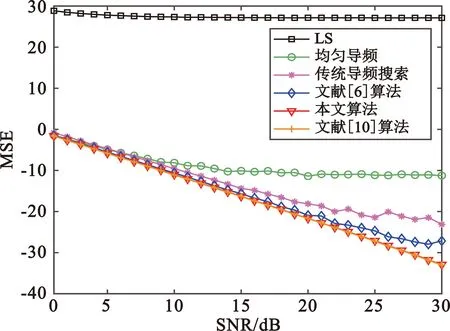
4.2 不同导频搜索算法性能比较


4.3 互相关准则运算选择比较
5 结束语
