要素替代弹性、价格加成对劳动收入份额的影响研究

钟世川

(重庆行政学院经济学教研部，重庆400041)

一、引言

现代经济学理论中，无论是经济增长的核算，还是要素收入份额的描述，总量生产函数的选择都起决定性作用。20世纪60年代，Solow最早提出采用Cobb－Douglas生产函数来研究总量经济行为。随后，C－D生产函数在新古典经济增长理论中得到广泛应用，主要原因在于它具有要素收入份额保持不变的性质，这一性质不仅为新古典经济理论中的经济达到稳定条件提供了依据，即C－D生产函数适合分析达到稳态水平的长期经济，而且还直接解释了“对单个经济体而言，要素收入份额在长期内应该保持不变”这一Kaldor事实，即要素收入份额等于其产出弹性。但遗憾的是，这样的事实并不成立。

要素收入份额的稳定性从20世纪80年代就已经开始遭到质疑，Blanchard等(1997)［1］利用C－D生产函数研究OECD国家1970～1995年的劳动收入份额变动情况，发现C－D生产函数失效，并且德国、法国、西班牙、意大利等OECD国家的劳动收入份额从1980年开始明显下降，而资本收入份额却从0.32上升到0.40。Harrison(2005)，［2］Guseina(2006)［3］以及 Acemoglu和 Guerrieri(2006)［4］等利用国民收入账户数据研究包括美国在内的OECD国家的劳动收入份额变动情况，发现OECD国家的要素收入份额并不稳定。目前采用C－D生产函数研究要素收入份额也都是基于产品市场完全竞争条件下进行的，并且证实大多数国家的要素收入份额在中期均存在波动现象(Bentolila and Saint－Paul，2003;［5］Choi and Rios － Rull，2009;［6］Rios－Rull and Santaeulalia －Llopis，2010［7］)。因此，对于要素收入份额变动的研究，C－D生产函数不具有有效性。

另外，C－D生产函数将技术进步设定为希克斯中性技术进步，即要素替代弹性被假设为1。但现实经济中的技术进步并非中性的，也不是外生的，而是有偏向性的，即要素替代弹性并非为1。从20世纪60年代起，国外众多经济学家就对要素替代弹性进行了测算:在希克斯中性技术进步假设下，Arrow等(1961)［8］测算出1909～1949年美国的要素替代弹性为0.57。Berndt(1976)［9］测算出1929～1968年美国制造业的要素替代弹性接近于1。Chirinko(2008)［10］使用美国的面板数据估计得出要素替代弹性在0.4～0.6之间。Klump等(2008)［11］使用欧洲地区的数据估计得出要素替代弹性为0.70。这些结论均作为支持使用C－D生产函数的强有力证据。然而，Antras(2004)［12］和 Young(2013)［13］利用现代经济增长理论对Berndt(1976)一文中的模型设定进行了分析，认为希克斯中性技术进步假设模型中忽略了变量偏误，从而导致要素替代弹性的估计值接近于1。同时，Antras通过构建有偏技术进步的计量模型，测算出美国要素替代弹性的估计值显著小于1，并得出美国经济不能用C－D生产函数进行研究的结论。据此，说明对于要素替代弹性的研究，C－D生产函数也不具有适用性。

相对于C－D生产函数，CES生产函数不仅取决于资本和劳动投入，而且还依赖于技术进步和要素替代弹性。CES生产函数中的替代弹性是大于0的常数，这不仅可以描述经济中长期的经济总量，而且还可以很好地刻画要素收入份额(Arpaia，et al.，2009;［14］Driver and Munoz －Bugarin，2010［15］)。前期研究也表明，要素收入份额与替代弹性之间存在着千丝万缕的联系:Gollin(2002)［16］认为，给定要素价格，要素收入份额由替代弹性和要素相对投入比例共同决定，当替代弹性大于1时，劳动的相对价格增加会使劳动收入份额增加，但后者增加的速度小于前者;当替代弹性小于1时，劳动的相对价格增加会使劳动收入份额减少;当替代弹性等于1时，替代弹性恰好抵消要素相对价格的改变。这说明替代弹性的取值对要素收入份额的变动具有决定性作用。

不同于C－D生产函数下的要素收入份额框架，CES生产函数中要素替代弹性不为1时，研究要素替代弹性对要素收入份额的影响可以提供更丰富的收入分配分析图景。但由于CES生产函数中替代弹性的测算研究在国内才开始起步，所以有关其作用影响的统计测算和计量经济分析也都刚刚起步;同时，目前对于要素收入份额变动的研究，都是在完全竞争市场条件下进行的，还未从非完全竞争市场条件下分析，即意味着劳动的边际产出不等于工资，本文将对这两个问题进行探讨。

由于替代弹性的取值决定了生产函数的具体形式，而CES生产函数包括了常用的几种生产函数，对于分析要素收入份额和要素替代弹性具有一般适用性，因此，本文基于非完全竞争市场，采用CES生产函数构建劳动收入份额和要素替代弹性的理论框架，并探讨其与增长率之间的关系。同时，本文采用蒙得卡罗近似估计方法测算1978～2013年中国要素替代弹性，并分析资本深化和价格加成对劳动收入份额的影响程度，以及测算劳动收入份额、价格加成对中国经济增长的贡献度。

二、理论框架分析

为了便于理论分析，假定技术进步只体现在劳动力水平上，即为劳动增强型的技术进步。将总量生产函数设定为CES生产函数，具体如(1)式所示:

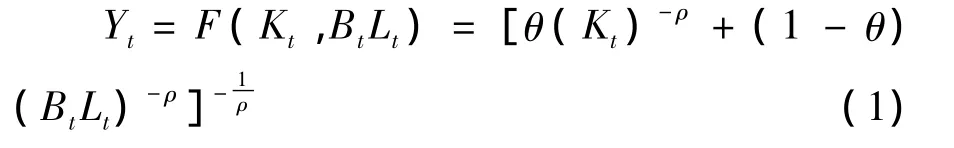
其中，Yt为产出，Kt为资本投入，Lt为劳动投入;Bt为劳动增强型技术进步指数;θ∈(0，1)是反映生产过程中两种要素重要性的分配参数，ρ=［(1－σ)/σ］是反映两种生产要素相互可替代性的替代参数，σ∈(0，∞)为要素替代弹性。

1.要素替代弹性、价格加成与劳动收入份额

对于企业而言，生产经营目标是利润最大化。记资本报酬率为rt，劳动报酬率为wt，总产出的价格为1，则企业的利润可以写为:

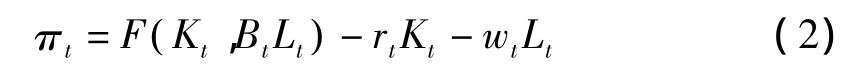
假设产品市场是不完全竞争的，记价格加成为χt，①在产品市场完全竞争的条件下，价格加成χt=1。利用利润函数(2)式对劳动Lt求导，有:

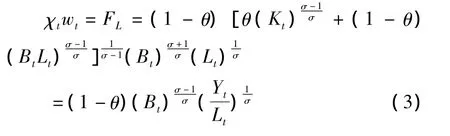
根据(1)式和(3)式，可得劳动收入份额βt的表达式为:

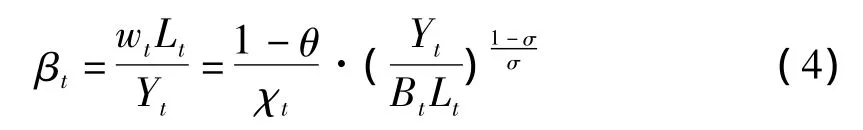
由(4)式可知，劳动收入份额βt的大小取决于价格加成χt、有效人均产出和要素替代弹性σ。

根据(1)式可得:

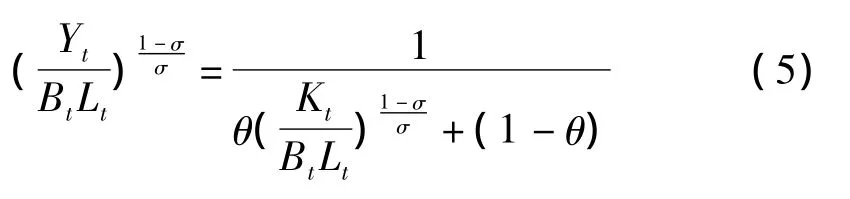
将(5)式代入(4)式，劳动收入份额βt变为:

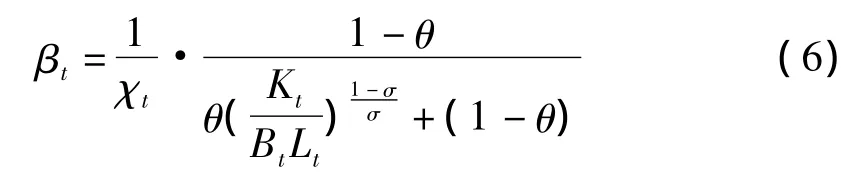
由(6)式可知，若价格加成χt保持不变，当要素替代弹性σ＞1时，有效资本深化使劳动收入份额βt降低;当要素替代弹性σ＜1时，有效资本深化使劳动收入份额增加;当要素替代弹性σ=1时，劳动收入份额的大小只取决于价格加成。若价格加成χt=1，则劳动收入份额的大小取决于有效资本深化。

由(1)式可得:

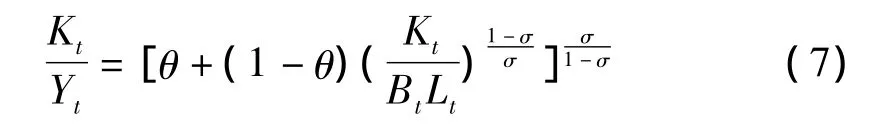
为了进一步分析价格加成、劳动收入份额与要素替代弹性的关系，根据(6)式和(7)式，劳动收入份额的表达式变为:

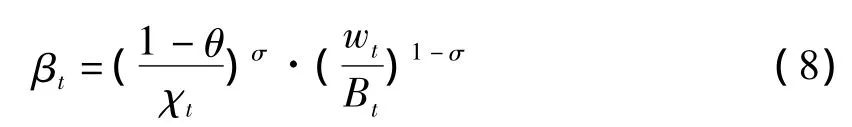
由式(8)可知，当σ＞1时，提高价格加成会导致劳动收入份额下降;相反，当σ＜1时，提高价格加成会使劳动收入份额上升。

2.价格加成和劳动增强型技术进步的测算

由于价格加成χt是未知参数，需要对其进行测算。Roeger(1995)，［17］Diewert和 Nakamura(2003)［18］利用欧拉定理和企业利润最大化的一阶条件对价格加成进行了测算，其表达式为:

由(9)式可得:

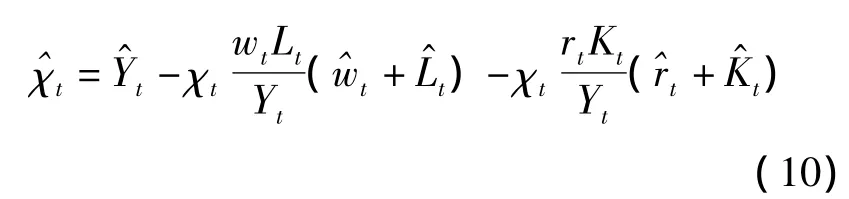
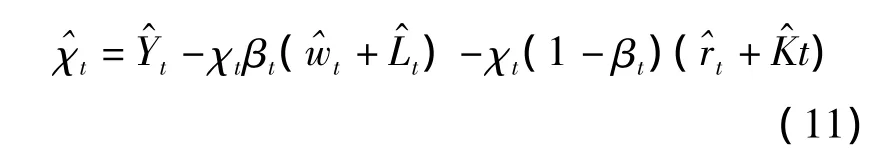
由(3)式可得劳动增强型技术进步指数的表达式为:

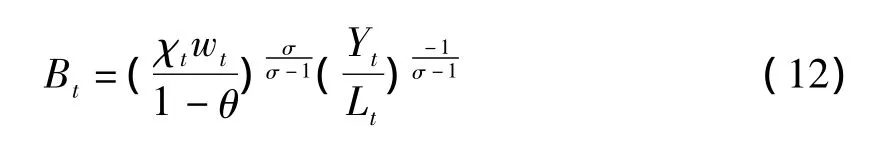
三、模型设定和数据说明

1.模型设定

将(6)式两边取对数，有:

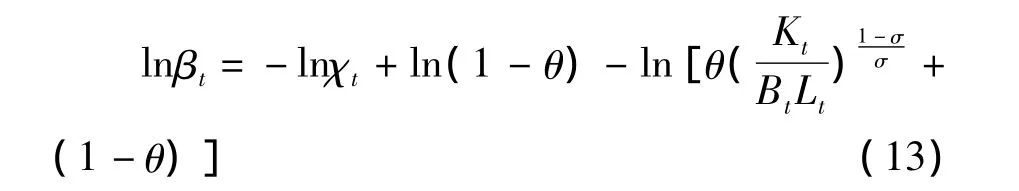
鉴于影响劳动收入份额变化方向的因素较多，如经济发展水平(李稻葵等，2009)、［19］技术创新、①Ortega D，Rodriguez F.Are Capital Shares Higher in Poor Countries?Evidence from Industrial Surveys.Fomento(CAF)and IESA，and Department of Economics，Wesleyan University，2006.外商直接投资②Zuleta H，Young A T.Labor's Shares－Aggregate and Industry:Accounting for Both in a Model of Unbalanced Growth with Induced Innovation.Available at SSRN 880062，2007.和国际贸易③Decreuse B，Maarek P.FDI and the Labor Share in Developing Countries:A Theory and Some Evidence，2008.是影响要素收入份额变动的主要原因，由于模型(13)为完全竞争条件下的线性模型，考虑到各种理论模型之外的因素作用和各种偶然因素的冲击，可将实证的计量模型设定为:

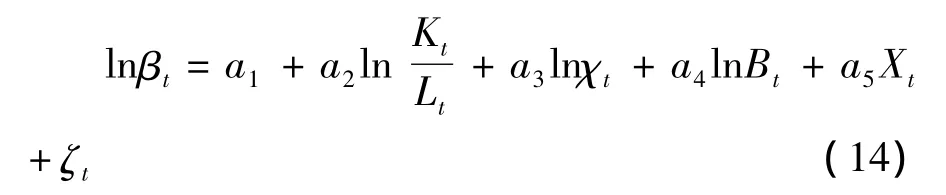
式中，βt表示劳动收入份额;Kt/Lt表示人均资本，该比值的增大称为资本深化，该比值的减小称为资本浅化，由于在经济发展过程中，资本可以积累而劳动不可以积累，因此，通常表现为资本不断持续深化的过程;χt表示价格加成;Bt表示劳动增强型技术进步。X表示一系列影响劳动收入份额的控制变量，包括:国际贸易(lnTradet)、外商直接投资(lnFDIt)和经济发展水平(ln(GDPt/Lt))。

2.数据说明

总产出数据:1978～2013年的国内生产总值GDP数据来源于各年的《中国统计年鉴》。利用各年现价GDP和实际GDP指数构造出GDP缩减指数，用此价格缩减指数对现价GDP进行缩减，便得到实际GDP，这就可以作为社会最终产品的总产出。以2000年的GDP价格指数为基期，从而计算得到的2000年价格GDP数据就可以看作是全社会各年的实际总产出。

资本投入数据:首先根据我国1953～1978年实际固定资本形成的年平均增长率和该期间固定资产的平均折旧率，估算得出1978年年末的全社会固定资本存量，其估算公式为:K0=，其中，K0为初始年份的资本存量，I0为初始年份的实际固定资本形成额，并以2000年价格计算1978年的固定资本形成额，g为初始年份以前各年实际固定资本形成的平均增长率，δ为平均折旧率。其次，将支出法GDP核算中每年固定资本形成的数据，用以2000年为基期的固定资产投资价格指数进行缩减，得出以2000年价格计算的每年实际固定资本形成额数据，并根据我国2004年和2008年两次经济普查得出的折旧率数据，根据永续盘存法公式:Kt=It+(1－δ)Kt－1(其中，以 1978 年为推算的初始年份进行递推计算)，得出各年年末的固定资本存量序列Kt。将每年年初和年末的固定资产存量相加并简单平均，得到每年的资本投入量。

劳动力投入数据:1978～2013年年末从业人员数数据来源于各年的《中国统计年鉴》，将相邻两年年末就业人员数简单平均得到各年的平均就业人数，将其看作各年劳动力投入数量。

要素报酬率数据:将各年收入法省级生产总值核算数据的每个项目的省份数据分别相加，计算得出1978～2013年全国各年最终产品初次分配中劳动者报酬、固定资产折旧、生产税净额、营业盈余4个分项的数据，用GDP价格缩减指数对每项数值进行缩减，得出各项的实际值。用实际劳动者报酬总额除以年平均从业人员数得到劳动报酬率wt，用实际固定资产折旧、实际营业盈余与生产税净额之和除以实际固定资本投入量得到资本报酬率rt，实际劳动者报酬总额除以实际GDP，得到劳动收入份额。

四、实证分析

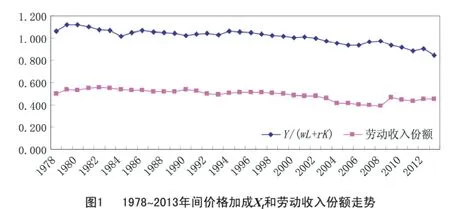
根据(9)式可以测算1978～2013年的价格加成χt，如图1所示:1978～2013年的价格加成整体呈下降趋势，其均值为1.012。2002年以前，价格加成大于1，但2002年以后，价格加成小于1。这说明我国的产品市场是非完全竞争的，即我国价格加成为1的假设不成立。从图1还可看出，1978～2013年的劳动收入份额整体也呈下降趋势，其均值为0.491。1978～1994年期间，劳动收入份额大致在51% ～56%之间;之后，劳动收入份额从1994年的50.3%下降至2007年的39.7%;2008年以后受世界金融危机和民工荒的影响，我国企业盈利水平下降，使得企业盈利占GDP的比重下降，因而2009年的劳动收入份额有所回升，其值为46.6%，但2013年劳动收入份额只有45.3%，仍低于20世纪90年代的水平。这说明要素分配份额的演变直接体现了国民收入分配格局的失衡，而且很有可能间接拉大我国居民之间的收入差距。

为了分析技术进步对劳动收入份额的影响，需要测算(12)式中的劳动增强型技术进步指数。首先测算要素替代弹性，采用蒙得卡罗方法(钟世川等，2014)［20］测算要素替代弹性的值，①将1978年设为初始年限 t0，且 t0=0，t∈［0，35］。测算结果显示:我国资本－劳动之间的替代弹性σ为0.486，说明我国资本与劳动之间呈互补关系;在生产过程中资本与劳动的重要性分配参数θ为0.474。值得注意的是，戴天仕和徐现祥(2010)［21］采用标准化系统方法测算出我国资本－劳动之间的替代弹性为 0.736，雷钦礼(2013)［22］采用利润最大化的线性一阶条件单方程估计方法测算出我国资本－劳动之间的替代弹性为0.382，而本文采用蒙得卡罗近似估计方法测算出的要素替代弹性介于前两者的测算值之间，原因在于测算方法和数据处理方法的不同，进而导致结果不同，但是无论采用何种测算方法，我国的要素替代弹性都大于0且显著小于1。其次将要素替代弹性值代入(12)式，可以得到劳动增强型技术进步指数的测算值，如表1所示:改革开放以来，劳动增强型技术进步指数呈上升趋势，1993年以后尤为明显。

表1 劳动增强型技术进步指数的测算值

利用(14)式进行实证分析，其估计结果如表2所示:模型(14)的估计结果与理论分析结论相一致。从OLS估计结果看:资本深化在1%水平上正显著，其每上涨1个百分点，劳动收入份额将上升0.085个百分点;价格加成也在1%水平上正显著，其每上涨1个百分点，劳动收入份额将上升0.109个百分点。国际贸易不显著，而经济发展水平和技术进步分别在1%和10%水平上正显著。值得注意的是，在资本深化过程中，我国在转轨经济时期的增长方式扭曲了要素价格，这种不对称的扭曲强度可能强化了劳动收入份额下降的趋势。

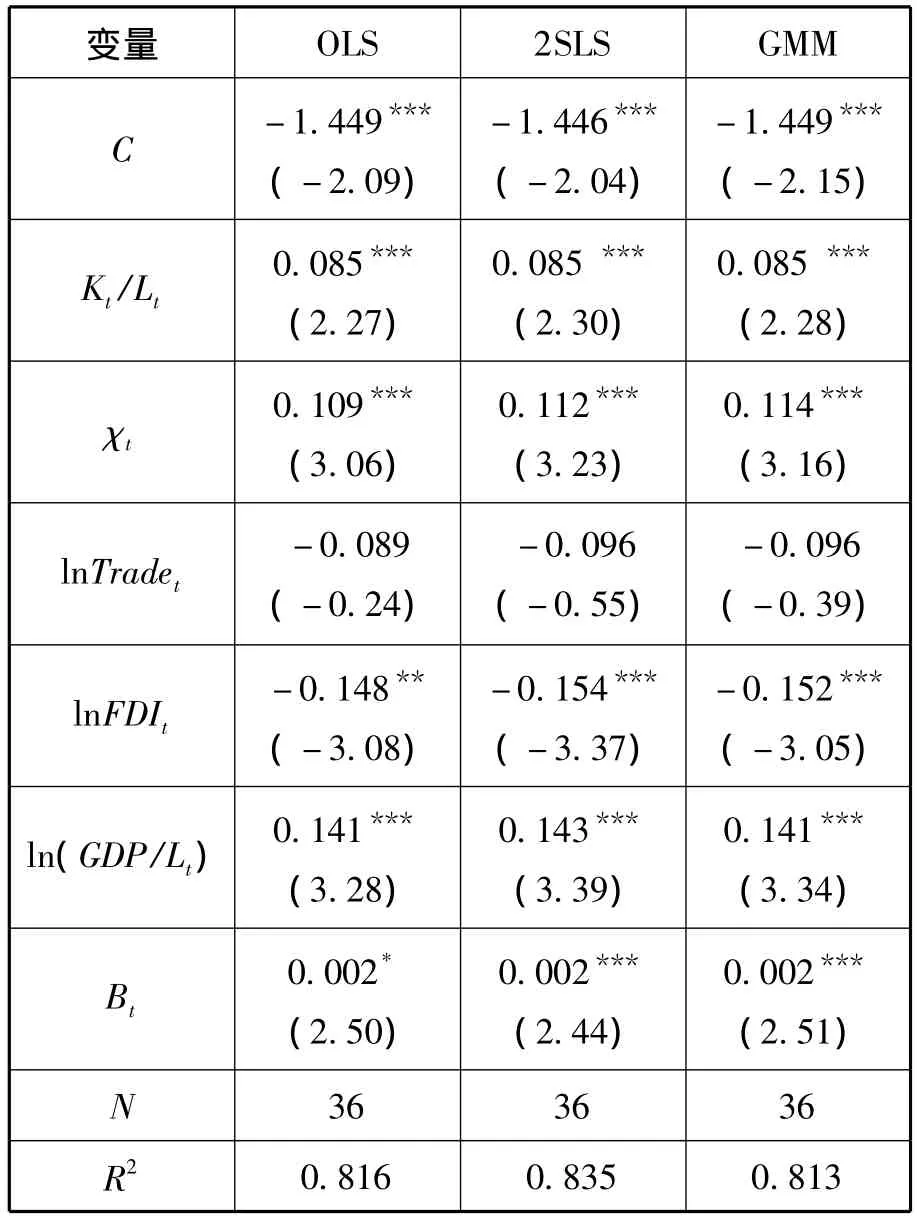
表2 价格加成、资本深化对劳动收入份额影响的估计结果

由于劳动收入份额与价格加成都是估计得到的，存在估计误差，并且劳动收入份额是价格加成倒数的组成部分，而劳动收入份额是随机变量，价格加成也应该是随机变量，这就违背了模型中解释变量非随机的假设，从而导致价格加成与ζt高度相关，估计结果显示模型(14)存在严重自相关。因此，选取资本收入份额的倒数作为工具变量来解决这一问题，因为资本收入份额的倒数也是价格加成的组成部分，与价格加成高度相关，经计算，模型(14)的残差与资本收入份额的倒数的相关系数为－0.035，这说明在一定程度上资本收入份额的倒数与ζt不相关，故选取资本收入份额的倒数作为工具变量，见表2中2SLS和GMM的估计结果。2SLS和GMM的估计结果显示，价格加成的系数分别为0.112和0.114，与OLS的估计结果相比，价格加成的系数更大，说明价格加成的提高对劳动收入份额的提升具有促进作用。除国际贸易的系数不显著外，其余变量的系数依旧显著。

五、结论及启示

在非完全竞争市场下，利用CES生产函数研究价格加成、要素替代弹性对劳动收入份额的影响。分析结论显示:当要素替代弹性大于1时，提高价格加成会导致劳动收入份额下降;当要素替代弹性小于1时，提高价格加成会导致劳动收入份额上升。在理论分析基础上，构建测算价格加成的方法，并使用我国1978～2013年的数据进行实证分析。测算结果表明，1978～2013年的价格加成和劳动收入份额整体呈下降趋势;2002年以前价格加成大于1，2002年以后价格加成小于1。测算结果也显示，1978～2013年间，我国要素替代弹性大于0且显著小于1，即我国资本与劳动呈互补关系，并且劳动增强型技术进步指数呈上升趋势。

进一步的实证分析表明，在要素替代弹性小于1的情况下，资本深化和价格加成均使劳动收入份额上升，这与理论分析结论相一致，也说明我国粗放型的增长方式扭曲了要素市场价格，这种不对称的扭曲强度可能加速了劳动收入份额下降的速度，即资本深化加速导致要素分配格局向资本倾斜，劳动收入份额表现出持续下降的趋势。实证分析结果还显示，劳动增强型技术进步和经济发展水平的提高有利于劳动收入份额上升，但国际贸易和外商直接投资却降低了劳动收入份额。从实证结果出发，在非完全竞争市场下，为了缩小要素收入分配差距:一是鼓励自主创新，因为自主创新在创新领域和创新路径的选择上都会更适合我国国情的发展，自主创新在提高技术吸收扩散效率的同时，更多地体现的是劳动增强型技术进步，这对于提升劳动收入份额有着积极作用;二是合理引进外资，适度减少进口，增加出口，这样才有助于提升劳动收入份额。

［1］Blanchard O J，Nordhaus W D，Phelps E S.The Medium Run［J］.Brookings Papers on Economic Activity，1997(2):89－158.

［2］Harrison A.Has Globalization Eroded labor’s Share?Some Cross－ country Evidence［R］.MPRA Paper No，2005:39649.

［3］Guseina A.Effects of Globalization on Labor's Share in National Income［R］.International Monetary Fund，Working Paper，2006.

［4］Acemoglu D，Guerrieri V.Capital Deepening and Non－Balanced Economic Growth［R］.NBER Working Paper，2006.

［5］Bentolila S，Saint－ Paul G.Explaining Movements in the Labor Share［J］.Contributions in Macroeconomics，2003，3(1):1103－1136.

［6］Choi S，Rios－Rull J V.Understanding the Dynamics of Labor Share:The Role of Noncompetitive Factor Prices［J］.Annals of Economics and Statistics/Annales d'É Conomie et de Statistique，2009:251－277.

［7］Rios－Rull J V，Santaeulalia－Llopis R.Redistributive Shocks and Productivity Shocks［J］.Journal of Monetary Economics，2010，57(8):931－948.

［8］Arrow K J，Chenery H B，Minhas B S，et al.Capital－Labor Substitution and Economic Efficiency［J］.The Review of Economics and Statistics，1961，43(3):225 －250.

［9］Berndt E R.Reconciling Alternative Estimates of the Elasticity of Substitution［J］.The Review of Economics and Statistics，1976(2):59 －68.

［10］Chirinko R.S.σ:The Long and Short of It［J］.Journal of Macroeconomics，2008，30(2):671－686.

［11］Klump R，McAdam P，Willman A.Unwrapping Some Euro Area Growth Puzzles:Factor Substitution，Productivity And Unemployment［J］.Journal of Macroeconomics，2008，30(2):645－666.

［12］Antras P.Is the US Aggregate Production Func-tion Cobb－Douglas?New Estimates of the E-lasticity of Substitution［J］.Contributions in Macroeconomics，2004，4(1):1161－1162.

［13］Young AT.Us Elasticities of Substitution and Factor Augmentation at the Industry Level［J］.Macro－ Economic Dynamics，2013，17(4):1－48.

［14］Arpaia A，Pérez E，Pichelmann K.UnderStanding Labour Income Share Dynamics in Europe［R］.MPRA Paper，2009:15649.

［15］Driver C，Mu～noz－Bugarin J.Capital Investment and Unemployment in Europe:Neutrality or Not?［J］.Journal of Macroeconomics，2010，32(1):492－496.

［16］Gollin D.Getting Income Shares Right［J］.Journal of Political Economy，2002，110(2):458－474.

［17］Roeger W.Can Imperfect Competition Explain the Difference Between Primal and Dual Productivity Measures?Estimates for US Manufacturing［J］. Journal of Political Economy，1995，103(2):316 －330.

［18］Diewert W E，Nakamura A O.Index Number Concepts，Measures and Decompositions of Productivity Growth［J］.Journal of Productivity A-nalysis，2003，19(23):127 －159.

［19］李稻葵，刘霖林，王红领.GDP中劳动份额演变的U型规律［J］.经济研究，2009，(1):70－82.

［20］钟世川，刘岳平.中国工业技术进步偏向研究［J］.云南财经大学学报，2014，(2):64－73.

［21］戴天仕，徐现祥.中国的技术进步方向［J］.世界经济，2010，(1):54 －70.

［22］雷钦礼.偏向性技术进步的测算和分析［J］.统计研究，2013，(4):83 －91.