冷链物流多级配送的安全库存优化研究

李昌兵 何亚辉 杨宇

摘要：冷链物流中不合理的安全库存将直接带来库存损失，进而影响冷链物流的经济效益。建立了3个多级冷链库存模型来对比和研究安全库存变化，并加入了符合现实状况的订货周期和符合一般维纳过程的需求量增量，在可变的变质率和相同的服务水平的情况下，对比发现增加配送中心和运营中心可以降低某些冷链食品的安全库存，进而减低其带来的库存损失。结果表明，在实际情况下，对于某些不宜装卸搬运的冷链食品，增加配送中心和运营中心所能带来的成本节省还存在不确定性。

关键词：冷链物流；多级配送；安全库存；一般维纳过程

中图分类号：F252 文献标识码：A 文章编号：0439-8114（2015）20-5136-04

DOI：10.14088/j.cnki.issn0439-8114.2015.20.053

Research on Safety Inventory Optimization of Multi-echelon Distribution

in Cold Chain Logistics

LI Chang-bing， HE Yu-hui， YANG Yu

（School of Economics and Management， Chongqing University of Posts and Telecommunications， Chongqing 400065， China）

Abstract： Unreasonable safety stock in cold chain logistics will result in inventory losses， there by affect the economic benefits of cold chain logistics. So three multi-level inventory models were established to compare and research the change of safety inventory， in addition the order cycle in accord with realistic conditions and the increment of demand in line with the general Wiener process were added， in case of the same service level and variable deterioration， it concluded that increasing the distribution center and operation center can reduce safety stock of some cold chain food， and thus reduce inventory losses. The results showed that， in practical， for some cold chain food unsuitable for loading and unloading， it's still uncertain about the cost savings by adding distribution center and operation center.

Key words：cold chain logistics； multi-echelon distribution； safety inventory； the general wiener process

在互联网时代，生鲜食品电子商务的发展远不如家电、服装等行业取得的成绩，主要瓶颈就在于冷链物流。冷链物流在发达国家属于成熟行业，在中国仍处于起步阶段。发达国家的农产品进入冷链流通达到95%，而中国仅5%，每年仅果蔬商品因运输储存不当的损失就有近千亿元[1]。因此冷链食品物流需要进一步研究和完善，其中冷链食品库存是冷链食品成本和收益的重要影响因素，也是影响资金成本和服务水平的重要因素。过多的冷链食品被暴露在非低温状态下，并且在售出的过程中被顾客不断触摸和挤压，增加了其变质的速度，增大了变质数量，造成了经济损失，因此控制冷链食品的库存水平有着重要的现实意义。合理的安全库存是冷链食品整体供应链优化的重要方面，故通过对冷链食品安全库存的优化，可以减少冷链食品的损失，降低成本。

Ghare等[2]首次在假设需求确定的情况下研究了易变质商品的单级库存优化模型；Sun[3]和Dong等[4]在瞬间补货、不允许缺货的前提条件下建立了易耗品的库存模型；Yang等[5]研究了供应商、零售商的冷链食品二级库存模型，通过建立一体化库存模型降低库了存成本；Shah等[6]在二级冷链库存模型中又加入残值性变量，在此基础上研究库存变化的情况，进而优化冷链食品库存；兑红炎等[7]针对一对多的易变质产品两级库存提出了通过横向调度来减少库存水平波动的方法；励凌峰等[8]则基于供应商、生产商、分销商三级供应链构建了集成化运作模型；李斌等[9]在需求率、变质率确定的前提下，将供应商和零售商的二级库存合作控制问题转化为一个生产商的自给自足生产问题，建立库存控制模型，优化了冷链食品的库存问题；张歆祺等[10]则为了优化冷链食品的库存而选择了联合库存管理模式；而蒋林等[11]研究了在模糊需求环境下三级供应链系统的库存策略及其最优决策；王淑云等[12]研究了固定变质率和生产率的三级冷链库存模型，以整个供应链利润最大化为目标，给出了包含生产商、分销商、零售商的冷链系统模型；许彤等[13]研究了冷链物流进出货速率对冷链物流库存的影响。本研究将通过建立多级库存减少安全库存的方式而减少库存成本、增加收益，并建立更加全面的多级库存优化模型，从而研究整条供应链的成本和收益变化情况，为冷链食品的多级库存管理提供更加完善的理论依据。

1 冷链食品多级配送库存模型

1.1 3种库存模式的模型假设

1）各零售商冷链食品的需求量属于正态分布。

2）各零售商和配送中心是相同且相互独立。

3）配送中心和运营中心由于存在冷冻设备而不存在产品变质情况，但在冷链食品运送到配送中心或者运营中心过程中，在装货和卸货时都会增加冷链食品的变质率。

1.2 3种冷链多级配送模型

冷链食品多级配送库存模型（3种模型都是零售商采取连续盘货，库存到达订货点时立刻补货的策略）：

1）冷链食品单级库存模型。冷链食品单级库存模型是由供应商直接将冷链食品配送给n个零售商进行销售。

2）加入一个配送中心的冷链食品多级库存模型。加入配送中心后，供应商将冷链食品先运送给配送中心，再由配送中心配送给其下辖的零售商。此时，配送中心将会承担保鲜和冷冻功能。

3）加入一个运营中心和m个配送中心的冷链食品多级库存模型。加入运营中心和配送中心后，供应商将冷链食品先运送给运营中心，再由运营中心配送给m个配送中心，再由配送中心配送给其下辖的零售商。此时，运营中心将承担保鲜盒冷冻功能，而配送中心不再储存冷链食品，仅提供配送功能。转运将会整合下游配送中心的需求，实现以下可能，即来自某个配送中心的高需求量将会被某个配送中心的低需求量所弥补。在运营中心，来自配送中心的需求量的变化所带来的总需求的变化将会减少。

1.3 模型中几个关键变量

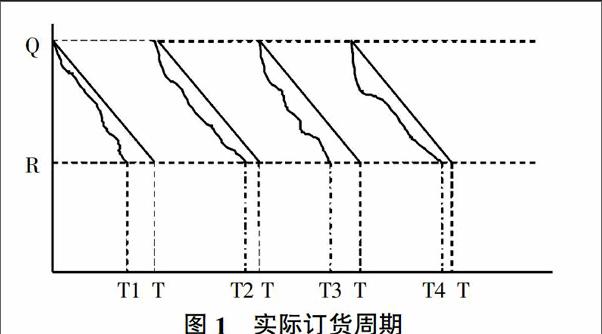
1.3.1 实际订货周期 与通常的一些固定的订货周期模型不同，实际中在连续盘货的情况下，当库存水平低于R时，零售商即开始补货，使库存达到Q，见图1。图1中曲线部分为实际需求波动下库存水平达到R时的周期，分别为T1、T2、T3、T4。周期是不断变化的，此周期与实际需求的性质有关。当需求波动时，订货周期存在提前到来的情况，如从T变为了T1。

1.3.2 需求量增量 一般维纳过程[14]说明未来的需求量只与现在的需求量有关，即人们在即将购买冷链食品时，只会考虑自身现在的需求量，而不会考虑过去的需求量，这与现实情况是相符合的。若独立变量x（t）的增量Vx符合正态分布，则

Vx=aVt+？滓Vw （1）

其中，Vt为时间的变化值，a为漂移率，即Vt内x均值的变化值，？滓为需求量的标准差，Vw为高斯白噪音，标准差为？滓■。

需求量x在Vt内的变化值Vx为动态过程，Vx由两部分组成，第一部分aVt为确定项，Vw为在此动态过程上添加的噪音，此时添加的噪音为高斯白噪音。在模型的假设中，假设需求量符合正态分布，即x：N（μ，？滓）为连续的独立增量，则Vx为一般维纳过程。证明如下：t1、t2分别为两个不同的时间点，其中t2>t1，将[t1，t2]分为n段，令

Δ=■

则xt2-xt1=[xt2-x（t2-Δ）]+[xt2-x（t2-2Δ）]+…+[xt2-x（t2-nΔ）]=■yi

由上述条件可知，当n→∞时，即Δ→0时，yi=x[w-（i-1）Δ]-x[w-iΔ]→0，由中心极限定理可得xt2-xt1趋于正态分布，即可得证。

1.3.3 安全库存 安全库存即由于需求的不确定性，预先设定的库存不能满足需求量而设定的库存。安全库存的数量将直接影响资金成本，过多将造成冷链食品的变质量加大，而安全库存过少，将会影响顾客的服务水平，所以合理安排和控制安全库存是控制成本和提高顾客服务水平的重要手段之一。对于需求量符合正态分布且其增量符合一般维纳过程的安全库存计算公式为：

ss=d×k×？滓（T） （2）

其中，ss为安全库存；■为需求量的均值；k为安全系数，通常为服务水平的函数，k=F-1（CSL），F（X）为需求量的正态分布函数，CSL为服务水平；T为实际订货周期（图1），即零售商两个订货点中间的时间间隔；？滓为标准差，指订货周期T的标准差。

对于供应链中的某级库存，认为是离供应商最近的一级库存，对于模型一为零售商，对于模型二为配送中心库存，对于模型三为运营中心库存。设开始库存水平为Q，在Ti内的平均需求量为D，x0=Q， x1=Q-D×T1，Δx=x0-x1，Δx=-D×T1，若ΔT=T，则

Δx=-D×T （3）

当ΔT=T时：由（1）式可得，D（Δx）=D（aVt+？滓Vw）=？滓2T（4）

由（3）式可得，D（Δx）=D（-D×T）=D2×D（T）（5）

由（4）、（5）可得，？滓2T=D2×D（T）

所以D（T）=■又因为T=■，所以

D（T）=■，又k=F-1（CSL）

又由（2）式可得，ss=d×F-1（CSL）×■=d×F-1（CSL）×■ （6）

3 3种模型的安全库存求解及对比

3.1 相关变量的符号表示

为便于对各级库存进行分析，对本研究中涉及的变量进行说明，如表1所示。

3.2 模型的安全库存

1）模型①：冷链食品单级库存模型是由供应商直接将冷链食品配送n个零售商，此时，单个零售量的安全库存为：

ss=d×F-1（CSL）×■

则n个零售商的总安全库存为

ss=n×F-1（CSL）×■ （7）

2）模型②：加入一个配送中心后，供应商将冷链食品先运送给配送中心，再由配送中心配送给其下辖的零售商，则n个零售商的总安全库存将表现为配送中心的安全库存，相当于集中存储对安全库存的影响，此时，配送中心需求量标准差的均值分别为？滓2G=n×？滓2s、■G=n×■s，则n个零售商的总安全库存为：

ss=n×d×F-1（CSL）×■=d×F-1（CSL）×■=F-1（CSL）×■ （8）

3）模型③：此时n个零售商的总安全库存为运营中心的安全库存，此时运营中心需求量标准差的均值分别为？滓F2=n×m×？滓2s、■F=n×m×■s，则n个零售商的总安全库存为：

ss=n×d×F-1（CSL）×■=d×F-1（CSL）×■=■×F-1（CSL）×■ （9）

3.3 模型对比

通过对比3种模型的安全库存可知，模型②的安全库存是模型①的1/n，模型③是模型①的1/nm，故增加配送中心和运营中心可以减少安全库存，且随着m的增大模型③的安全库存量减少的越大。

设因为设立运营中心和配送中心而引起的变质率随着转运次数的增加而增加，即■=？坠，其中，w为转运次数，即在模型②中，转运次数为1，则？兹=？坠，在模型③中增加了两次转运，则？兹=2？坠。

3.3.1 模型②与模型①对比分析 虽然安全库存减少了，但是由于增加了转运次数，因此增加了？兹=？坠的变质率，设z=■，P为冷链食品的价格。因此实际减少的安全库存成本为（n-1）F-1（CSL）zp（1-？坠）。由于增加了配送■=？坠中心带来的变质率的增加引起的库存成本损失为？坠npQs。

为了考虑一个周期内由于安全库存变化而引起的成本变化，不考虑建设配送中心的固定成本，仅考虑c1、c2，则一个周期内增加配送成本带来的总成本为c1+c2nQs。

故安全库存成本的减少量与总成本的增加量的差值即为增加配送中心带来的总收益，为：

H1-2=（n-1）F-1（CSL）zp（1-？坠）-？坠npQs-c1-c2nQs=（n-1）F-1（CSL）zp-[（n-1）F-1（CSL）zp+npQs]？坠-c1-c2nQs （10）

当H1-2=0时，？坠=■（11）

当冷链食品的变质率随着装卸搬运次数的增加而增加时，某些冷链食品（如未进行完整包装的樱桃、车厘子等）增加的变质率会达到或超过上式值，故对于这些种类的冷链食品，增加配送中心并不能带来成本的收益。

3.3.2 模型③与模型①对比 虽然安全库存减少了，但是由于增加了转运次数，因此增加了？兹=2？坠的变质率，实际减少的安全库存成本为（n-■）F-1（CSL）zp（1-？坠）。由于增加了运营中心和配送中心带来的变质率的增加引起的库存成本损失为2？坠npQs

为了考虑一个周期内由于安全库存变化而引起的成本变化，不考虑建设配送中心的固定成本，配送中心不再承担储存冷链食品的任务，不考虑c2仅考虑c1、c3、c4，则一个周期内增加配送成本带来的总成本为c3+c4nQs+c1m。

故安全库存成本的减少量与总成本的增加量的差值即为增加运营中心和配送中心带来的总收益，为：H1-3=（n-■）F-1（CSL）zp（1-2？坠）-2？坠npQs-c3-c4nQs-c1m=（n-■）F-1（CSL）zp-[（n-■）F-1（CSL）zp+npQs]2？坠-c3-c4nQs-c1m （12）

当H1-3=0时，？坠=

■（13）

当冷链食品的变质率随着装卸搬运次数的增加而增加时，某些冷链食品（如未进行完整包装的樱桃、车厘子等）增加的变质率即可达到或超过上式的值，所以对于这些种类的冷链食品，增加运营中心和配送中心并不能带来成本的收益。

在冷链食品的种类确定时，其随着装卸搬运次数增加而增加的变质率是已知的，即？兹是已知的，此时：■=■ （14）

当■=0时，m=■，即此时m的取值可以使H1-3最大，即增加的收益最大，而1≤m≤n，所以，■与n比较即可得出最优的m取值。故增加的配送中心的数量并不是越多越好，而是与z、p、c1、？兹、F-1（CSL）有关。

4 结论

本研究利用一般维纳过程体现更符合实际的需求量，利用最新的安全库存计算方法，并加入可增大的变质率变量，从冷链食品供应链的角度出发，构建了多级库存的供应链优化模型。结果表明，对于某些冷链食品，增加配送中心和运营中心，可以减少安全库存，进而带来总成本的降低，优化供应链，增加收益，但是此时也要合理的配置配送中心的数量。

而对于装卸搬运时会引起变质率大幅增大的冷链食品，增加配送中心和运营中心虽然能够减少安全库存，但是会带来总成本的不变或增加，此时，不能靠增加配送中心和运营中心来优化冷链食品的供应链。另外，本研究只针对安全库存及其带来的影响进行研究，并无加入时间节点对冷链库存的变质率进行详细的研究，这需要下一步进行深入的探讨和研究。

参考文献：

[1] 凤凰网.冷链物流行业整合发展[EB/OL].http：//news.ifeng.com/a/20140923/42056783_0.shtml.

[2] GHARE P M， SCHRADER S F.A model for exponentially decaying inventory[J]. Journal of Industrial Engineering，1963，14：238-243.

[3] SUN Y J. Global stabilizability of uncertain systems with time-varying delays via dynamic observer-based output feedback[J].Linear Algebra Appl，2002，353：91-105.

[4] DONG Y，LIU J，MEI S，et al. Stabilization for switched nonlinear time-delay systems[J]. Nonlinear Analysis：Hybrid Systems，2011， 5：78-88.

[5] YANG P C， WEE H M. An integrated multi-lot-size production inventory model for deteriorating item[J].Computer & Operations Research，2003，30（50）：671-682.

[6] SHAH N H，GOR A S， WEE H M. Optimal Joint Vendor-buyer Inventory Strategy for Deteriorating Items with Salvage Value[M]. Wollongon， Australia： Australian computer Society， 2008.

[7] 兑红炎，李淑敏.带有横向调度的易变质商品两级库存系统分析与优化[J].工业工程，2010，13（2）：58-60.

[8] 励凌峰，黄培清.供应链中的易腐物品生产-库存协作研究[J].上海交通大学学报，2005，39（3）：464-467.

[9] 李 斌，潘秀娟.易变质商品的二级库存模型的合作策略[J].天津工业大学学报，2013，32（4）：76-88.

[10] 张歆祺，何 静.食品冷链联合库存管理模式的探析[J].江苏农业科学，2011，39（4）：545-546.

[11] 蒋 林，张怀胜.模糊需求环境下的多级供应链库存协调策略[J].工业工程，2010，13（2）：28-32.

[12] 王淑云.生产商-分销商-零售商一体化冷链库存模型[J].公路交通科技，2013，30（4）：132-140.

[13] 许 彤，蒋明霞.冷链物流进出货速率对库存影响的分析[J].物流技术，2012，31（8）：306-307.