一种具有自我更新机制的量子粒子群优化算法

奚茂龙，吴小俊，方伟，孙俊

1.无锡职业技术学院控制技术学院，江苏无锡214121

2.江南大学物联网工程学院，江苏无锡214122

◎博士论坛◎

一种具有自我更新机制的量子粒子群优化算法

奚茂龙1，2，吴小俊2，方伟2，孙俊2

1.无锡职业技术学院控制技术学院，江苏无锡214121

2.江南大学物联网工程学院，江苏无锡214122

自然界中生命体都存在着有限的生命周期，随着时间的推移生命体会出现老化并死亡的现象，这种老化机制对于生命群体进化并保持多样性有重要影响。针对量子行为粒子群（QPSO）算法中粒子存在老化并使得算法存在早熟收敛的现象，将生命体的自我更新机制引入了QPSO算法，在粒子群体进化中提出领导者粒子和挑战者粒子，随着群体粒子的老化，当领导者粒子领导力耗尽不能引导群体进化时，挑战者粒子通过竞争更新机制成为新的领导者粒子引导群体进化并保持群体多样性，并证明了算法的全局收敛性。将提出的算法与多种典型改进QPSO算法通过12个CEC2005 benchmark测试函数进行比较，对结果进行了分析。仿真结果显示，该算法具有较强的全局搜索能力，尤其在7个多峰测试函数中，综合性能最优。

粒子群算法；量子行为；自我更新机制；多样性；全局收敛；老化

1　引言

Kennedy等人在1995年模拟鸟群和鱼群的觅食行为提出了粒子群优化算法（Particle Swarm Optimization，PSO）［1］。在算法进化过程中，群体共享最优位置信息；在群体最优位置信息和自身最优信息引导下，通过搜索多维问题解空间，不断更新自身速度和位置，并不断追随和比较问题空间候选解，最终发现问题的最优解或局部最优解。粒子群算法具有进化方程简单、搜索能力较好、收敛速度快的特点，自提出以来已经成功应用在很多方面。但PSO算法本身并不是一种全局优化算法［2］，许多学者对它进行了大量的研究工作，提出了一些改进方法，取得了一定的改进效果［3-4］。在深入研究社会智能群体进化过程的基础上，Sun等人在分析了粒子群优化算法机理，将量子理论引入了PSO算法，提出了具有全局搜索能力的量子行为粒子群优化算法（Quantum-behaved Particle Swarm Optimization，QPSO）［5-6］。QPSO算法具有计算简单、编程易于实现、控制参数少等特点，引起了国内外相关领域众多学者的关注和研究。Xi等人在计算QPSO算法的平均最优值时，根据粒子的优劣程度引入了非线性权重系数，提升了算法的寻优能力［7］；Sun等人在文献［8］中给出了QPSO算法的粒子行为分析以及参数选择方法；文献［9］在QPSO算法中引入了变异算子，改善算法全局搜索能力。同时，QPSO算法也成功应用于许多实际问题，Omkar等人将QPSO算法应用于组合结构的多目标优化问题［10］，Indiral等人将QPSO算法应用于关联规则挖掘［11］，同时算法也在投资组合选择问题中得到了应用［12］。

群体智能算法中，一直存在着如何平衡收敛速度和全局寻优能力的问题，而老化（aging）是生命群体的个体不可避免的生命进程，群体中粒子老化并被新的粒子替代可以有益于群体进化结构，能够提升群体的多样性。QPSO算法是一种典型的群体智能算法，同样在进化后期存在粒子老化现象，容易陷入局部最优，文章提出在QPSO算法中引入领导者粒子和挑战者粒子机制，实现群体的自我更新，提升群体多样性并跳出局部最优能力；并研究了粒子老化过程中的领导力、生命周期、更新规则等要素，提出了一种具有自我更新机制的改进量子粒子群优化算法（QPSO with self-renewal mechanism，SMQPSO）。通过matlab编程，选取经典高维测试函数，在不同自我更新机制参数下进行了反复测试；并和QPSO及其他改进算法进行了比较分析，证明了该算法能够显著提高搜索效率和全局优化性能。

2　量子粒子群优化算法（QPSO）

在PSO算法中，使用了群体最优位置信息（global best position，Pg），个体最优位置信息（personal best position，Pi），粒子的速度信息Vi和位置信息Xi。基本粒子群算法的进化方程为：

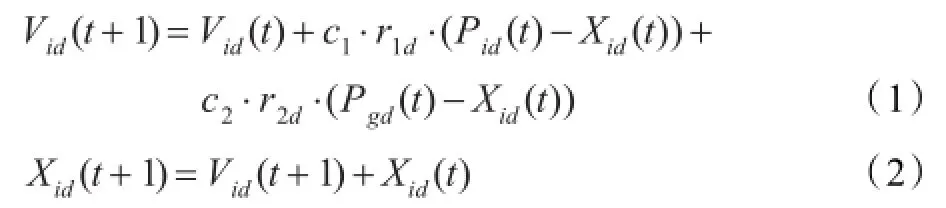
通过对PSO算法中粒子运动轨迹的详细分析，Clerc等人［13］指出如果每个粒子都能够收敛到它的局部吸引点P′i=（P′i1，P′i2，…，P′iD），那么PSO算法可能收敛。其中

式（3）中，t是算法当前迭代次数，r1d（t）和r2d（t）是［0，1］之间的随机数，Pid为粒子的当前最优位置d维值，Pgd为群体的全局最优位置d维值。

在量子理论中，量子空间粒子的速度和位置是不能同时确定的，这更符合智能群体进化决策过程，每个粒子的状态都由波函数ψ来确定，|ψ|2是粒子位置的概率密度函数。Sun等人将PSO算法的进化系统假设为量子系统，在粒子群算法第t次迭代，粒子i在D维的空间运动，该粒子在第j维的势阱为P′ij（t），则在第t+1次迭代可以得到粒子i的波函数为：

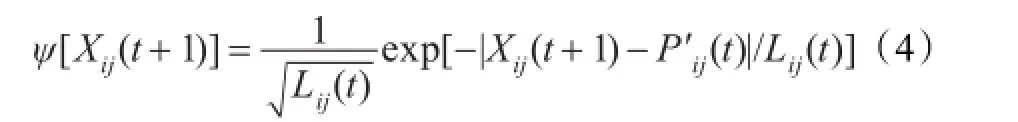
则概率密度函数Q为：

概率分布函数F为：

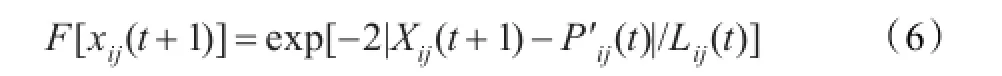
应用Monte Carlo方法，可以计算出在第t+1次迭代，第i粒子第j维的位置：

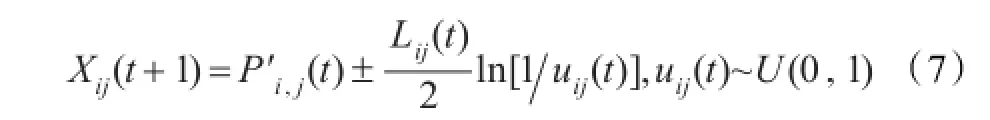
其中Lij（t）的值由下式确定：

式（8）中M称为平均最优位置，也记为mbest，是所有粒子自身最优位置的中心点，由下式计算得到：

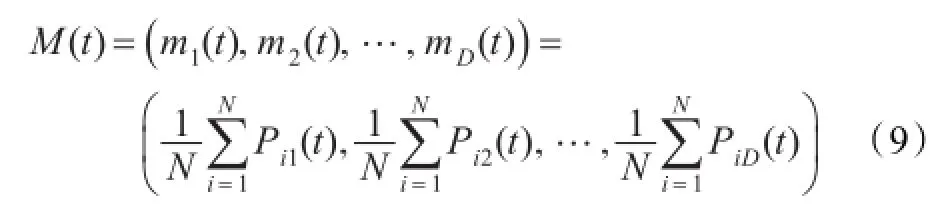
其中N是群体规模的大小，Pi是第i个粒子自身最优位置。因此，可以得到粒子的位置更新方程：

式

（10）中，β称为压缩扩张因子，用来调节粒子的收敛速度。

粒子当前最优位置Pi和全局最优位置Pg的更新方式与基本PSO算法的更新方式完全相同，即

这里粒子位置更新公式（10）的PSO算法为具有量子行为的粒子群优化算法（Quantum-behaved ParticleSwarm Optimization，QPSO）［5-6］。

3　一种具有自我更新机制的QPSO算法

3.1QPSO算法中粒子进化分析

为了研究QPSO算法中群体每个粒子进化迭代过程，提出了相对进化速度概念。个体粒子的相对进化速度可以通过式（13）进行定量的计算描述。

其中，fi是第i粒子的当前适应度函数值，fPi是粒子i个体的最优适应度函数值（最小化问题），如果Δf的值接近于0或等于0，表明粒子进化基本停止不前，群体粒子可能陷入了局部区域。本文使用了CEC2005 benchmark标准测试函数［14］，在这些测试函数中f1～f5为单峰问题函数，f6～f12为多峰函数。图1给出了群体粒子为20，变量维数为10维，迭代次数10 000次的条件下，使用QPSO算法测试f1函数的粒子进化过程，不同的颜色代表不同的粒子。图2给出了群体粒子为40，变量维数为30维，迭代次数10 000次的条件下，使用QPSO算法测试f6的粒子进化过程。

图1　使用QPSO算法优化f1函数的粒子进化过程

图2　使用QPSO算法优化f6函数的粒子进化过程

从图1粒子群体的进化过程可以看出，对于f1测试函数，在进化初期，各个粒子Δf的值变化较大，群体能够处于较优的进化状态；在进化的后期，各个粒子Δf开始有一定的聚集，群体粒子的进化速度逐步下降，在一定程度上停滞于局部最优区域。对于图2中的f6测试函数，由于是变换多峰函数，寻优难度更大，在迭代次数为3 500次之前，群体还有较好的进化性能，但到了5 000次迭代后，群体粒子的Δf迅速聚集在0值附近，在后续的迭代过程中不再变化，即粒子已全部聚集到较小区域的附近，并只在解的邻近小区域进行搜索。可以知道，一旦算法在搜索过程中陷入局部最优，往往很难跳出局部最优解区域，继续全局最优解的搜寻。从图1和图2分析可知，QPSO算法容易在进化后期陷入局部区域的搜索，需要通过一定的更新机制增加群体的全局搜索能力。

3.2算法思想

在QPSO算法中，粒子的进化过程是通过迭代方程（3）（9）（10）实现的。群体粒子的更新依赖于自身最优（Pi）和全局最优（Pg）的粒子信息，由Pi和Pg引导粒子进行解空间范围内的寻优。在这种搜索机制下，当群体粒子被吸引到一个局部最优范围时，由于Pi和Pg的吸引作用，随着迭代次数的增加，Pi和Pg并没有得到更新，群体的多样性降低，因此群体很难跳出局部最优范围，在更大范围中寻优，影响了算法的寻优性能。

在SMQPSO算法中，为了增加群体粒子的多样性，防止长时间陷入局部最优，引入了有生命周期的领导者粒子（Leading Particle），替换基本QPSO算法中的Pg，文中称为Pleader。不同于文献［9］中直接引入变异算子策略，本文的领导者粒子需要在迭代过程中不断评价领导者粒子的领导力（Power），判断当前领导者粒子是否能够继续引导群体寻优，从而判断领导者粒子是否需要更新；同时，对于个体自身最优Pi也引入了生命周期的概念，文中称为Pi_l，在一定条件下，如果个体粒子不能寻优，也需要进行更新。因此，对于SMQPSO算法，进化方程（3）（9）（10）修改为：

3.3粒子的生命周期

在SMQPSO算法，粒子的生命周期（life time）对于算法的性能是很重要的。SMQPSO算法中，粒子在进化过程中存在的时间采用了动态生存时间概念，通过测量粒子以往和现在的表现提出粒子领导力（leading power），通过领导力评价粒子能否继续引导群体或自身进化，并判断是否需要更新。

粒子的领导力是通过在群体历史进化过程中，引导群体或个人进化表现累积的。对于Pleader，在引导群体粒子进化过程中，有四种情况：（1）引导了群体进化和个体进化；（2）引导群体进化，而个体没有进化；（3）引导个体进化，而群体没有进化；（4）群体和个体都没有进化。对于Pi_l，在引导个体进化过程中，有两种情况：（1）引导了个人进化；（2）没有能够引导个体进化。对于最小化问题，可以将粒子的领导力通过公式（17）（18）（19）表示出来。

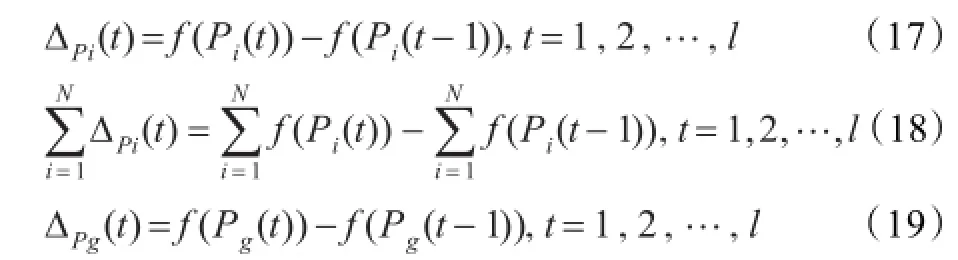
其中，ΔPi（t）表示个体粒子引导自身进化的领导力，表示Pleader引导群体进化的领导力，ΔPg（t）表示个体最优进化的引导力，l表示相应粒子的生命周期。文中，用Powerleader表示Pleader的领导力，Poweri_l表示群体中第i个粒子的领导力，则粒子的领导力分析为：

（5）当ΔPi（t）＜0时，说明Pi_l领导力强，则Poweri_l= Poweri_l+ζ1。

（6）当ΔPi（t）＞0时，说明Pi_l领导力差，则Poweri_l= Poweri_l+ζ2。

在SMQPSO算法进化过程中，根据累积领导力，判断粒子是否需要更新。

3.4领导粒子更新

领导粒子在进化过程中，领导力随着进化过程不断动态变化。当领导粒子在一轮迭代进化过程中，引导了群体进化，则领导力累积增加；当领导粒子没有能够引导群体进化，则领导力下降。通过判断每一轮的进化结果，计算领导粒子的领导力。当领导粒子的领导力消耗殆尽，则意味着群体粒子陷入了局部最优，领导粒子没有能力继续引导群体寻优。在这种情况下，就必须有新的粒子作为领导粒子引导群体寻优，文中将新的粒子称作潜在领导粒子（Pcandidate），需要进一步判断潜在领导粒子是否能够作为领导粒子引导群体寻优。

为了保证领导粒子结构的完整性，并考虑运算复杂度因素，文中采用了对Pleader的每一维按照一定的概率（pro）初始化的方式产生Pcandidate。按照均匀分布的方式在（0，1）中产生一个随机数（rndj），如果rndj＜pro，Pleader粒子对应的j维数值在解空间（Lower，Uper）中重新初始化；如果在此过程中，没有任何一维能够满足条件初始化，则随机指定Pleader中的一维初始化，产生Pcandidate。具体过程如图3所示。

图3　领导粒子的更新过程

由于领导者粒子并不是每一轮进化都进行更新，在最极端情况下，每一轮进化群体都不能寻找到更优值，领导者粒子的更新次数和进化迭代次数m相同，即m次进化后，领导者粒子计算更新了m次，则时间复杂度为O（m）。

同样，对于个体引导粒子Pi_l的领导力消耗完后，也需要一个产生个体引导候选粒子Pi_l_candidate，过程同Pcandidate产生过程。Pcandidate和Pi_l_candidate产生后，还需要评价它们的领导力，是否能够引导群体寻找问题的更优解。

如果f（Pcandidate）＜f（Pleader），说明群体领导候选粒子Pcandidate是合适的，则Pleader=Pcandidate；反之，是不合适的，继续使用原来Pleader引导当前迭代进化。

如果f（Pi_l_candidate）＜f（Pi_l），说明个体领导候选粒子Pi_l_candidate是合适的，则Pi_l=Pi_l_candidate；反之，是不合适的，继续使用原来Pi_l引导当前迭代进化。

SMQPSO算法设计如图4所示。

图4　SMQPSO算法过程

4　SMQPSO算法的收敛性分析

4.1搜索算法的全局收敛性准则

在本文分析SMQPSO算法收敛性过程中，使用t表示迭代次数，S表示解空间的一个子集，z表示解空间中的点。根据Solis和Wets提出随机搜索算法的收敛性准则［15］，随机算法应满足假设1：

假设1f（D（z，τ））≤f（z），并且如果τ∈S，则其中，D表示具体算法，τ表示样本空间的向量。

任何算法的全局收敛意味着序列｛f（zt）｝∞t=1应收敛于函数f在S中的下确界。为避免函数的病态（最小值点在间断点）以至于搜索不到全局最优解，将搜索目标变为搜索下确界ψ，则可以无需遍历S中的每个点就可以接近下界。定义算法可接受区域为：

其中，ε＞0。如果算法找到Rε中的点，则称算法找到了误差为ε的可接受点。因此，对于最小化问题，全局收敛算法应该满足假设2。

假设2对于S的任意Borel子集A，若其测度v［A］＞0，则有

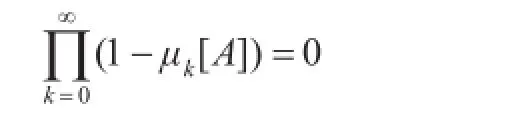
其中，μk［A］是由测度μk所得到A的概率。这就是说对于位置测度为v的任意一个A的子集，如果采用随机取样的方法，那么它重复错过集合A的概率必定为零。由于Rε⊂S，所有在可接受区域取得点的概率肯定是非零值。基于以上分析，可以得到下面定理：

定理1假设目标函数f为可测函数，S为可测解空间子集，满足假设1，设｛zk｝∞k=0为算法生成的解序列，可得

其中，P［zk∈Rε］是第t步算法生成的解zk∈Rε的概率。

4.2SMQPSO算法全局收敛性证明

本文在SMQPSO算法收敛性证明过程中将它置于全局随机搜索算法的框架中研究，以定理1的结论进行证明，则有如下引理。

引理1 SMQPSO算法满足假设1。

引理2 SMQPSO算法满足假设2。

证明在SMQPSO算法阐述中，在任意一个迭代步t，在i个粒子第j维的概率密度函数为：

定义μi，t为对应于Q（Xi，t）的概率测度，对于S的任意Borel子集A，当满足v［A］＞0，则可得到

和

其中，Mi，t是μi，t在样本空间的支撑，并且A⊃Mi，t。因此可以得到

粒子的支撑联合为：

其中，Mt是分布μt的支撑，由μt生成的概率A可以由下式计算得到

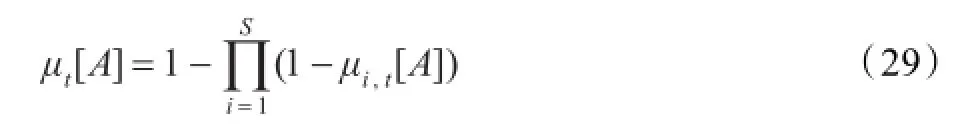
通过式（27），可以得到：

因此可得：

表明SMQPSO算法满足假设2。证明完毕。

5　SMQPSO算法仿真分析

5.1粒子领导力参数分析

在SMQPSO算法中，粒子领导力参数（δ1，δ2，δ3，δ4，ζ1，ζ2）的取值对算法有重要的影响，本文通过不同的参数取值组合对参数进行研究。测试函数使用CEC2005 benchmark测试函数［14］，其中f1到f5为单峰函数，f6到f12为多峰函数。算法中，其他的参数设置为：收缩扩张因子β从1.0线性下降到0.5，问题维数为30，算法对应的最大迭代次数为20 000，粒子数为40；每个问题的求解都应用算法随机地独立运行50次，pro取值为1/D。表1给出了领导力参数不同取值条件下时，目标测试函数值的平均值和标准方差。在领导力参数取值中，对于Pleader粒子领导力的不同情况，δ1，δ2，δ3分别取值（2，1，0）；对于δ4研究了两种取值情况，分别是-1和-2，当Pleader不能领导群体寻优时，δ4取值-2能够快速地消耗Pleader前期累积的领导力，达到快速更新Pleader的目的，当领导力耗尽时，粒子的生命周期就结束了。对于个体粒子领导力ζ1，ζ2研究了（2，-1）、（2，-∞）和（3，-1）的情况，其中-∞表示当粒子不能领导个体寻优时，直接进入粒子更新步骤，不再考虑前期累积的领导力。

由表1中的仿真数据可以得出，不同的领导力参数组合对算法性能是有影响的。对于单峰函数（f1～f5），优化问题相对简单，粒子陷入局部最优的可能性较小。当领导粒子陷入局部最优时，快速地减小它的领导力，使得新的粒子尽快替代它，能够领导群体继续寻优。对于多峰函数（f6～f12）则正好相反，优化问题相对复杂，在优化过程中粒子容易陷入局部最优，而领导粒子积累了相对较多的领导力，采用较小的领导力下降速度值将有利于保持群体的寻优结构，并最终找到最优值。

表1　不同领导力参数条件下SMQPSO算法的测试函数平均值及方差

5.2仿真结果与讨论

表2和表3给出了文中提出的SMQPSO算法和其他典型改进QPSO算法的仿真结果比较。这些比较的算法主要有固定收缩扩张因子的QPSO（BQPSO）算法、标准QPSO（QPSO）算法、局部搜索策略的QPSO（LCQPSO）算法、自学习QPSO（SQPSO）算法、强化学习的QPSO（QLQPSO）算法、最优吸引点QPSO（GQPSO）、混合吸引点QPSO（HQPSO）算法、线性权重系数QPSO（WQPSO）算法和非线性权重QPSO（UQPSO、DQPSO）算法［5-7，15-16］。在所有算法测试中，问题维数为30，算法对应的最大迭代次数为20 000，粒子数为40，每个问题的求解都应用算法随机地独立运行50轮，其他参数设置与原参考文献相同。

表2和表3中的结果比较显示，在测试函数Schwefel’s Problem 2.6 with Global Optimum on the Bounds函数（f5）、Shifted Rotated Griewank’s Function without Bounds函数（f7）、Shifted Rotated Ackley’s函数（f8）、Shifted Rastrigin’s函数（f9）、Shifted Schwefel’s Problem 1.2函数（f12）取得了较好的值，在f5、f8、f9测试函数中取得了第一，是所有测试算法中最多的，在其他的测试函数中也取得了和其他算法相近的仿真结果。BQPSO算法、QPSO算法、LCQPSO算法、GQPSO算法、HQPSO算法、UQPSO算法、WQPSO算法则分别在Shifted Rotated Weierstrass函数（f11）、Shifted Rotated High Conditioned Elliptic函数（f3）、f7、Shifted Sphere函数（f1）、Shifted Rotated Rastrigin’s函数（f10）、Shifted Rosenbrock函数（f6）、f12中分别取得了一次最优值，QLQPSO算法在Shifted Schwefel’s Problem 1.2函数（f2）、Shifted Schwefel’s Problem 1.2 with Noise in Fitness函数（f4）中取得了二次最优值。图5给出了QPSO算法、PSO算法、SMQPSO算法、QLQPSO算法和SQPSO算法的20 000次迭代的进化曲线比较。从收敛曲线可以看出，SMQPSO算法和PSO算法相比较，在12个测试函数中都能够取得较快的收敛速度；和QPSO算法相比较，在测试函数中能够有相接近的收敛速度，在f3、f9、f10和f11中的收敛速度要优于QPSO算法；和其他QPSO的改进算法比较，虽然不能在所有的测试函数中取得明显优势，但是收敛性能稳定，综合性能好。以上说明，提出的具有自我更新机制的QPSO算法，能够提升跳出局部搜索的能力，提升算法整体性能。

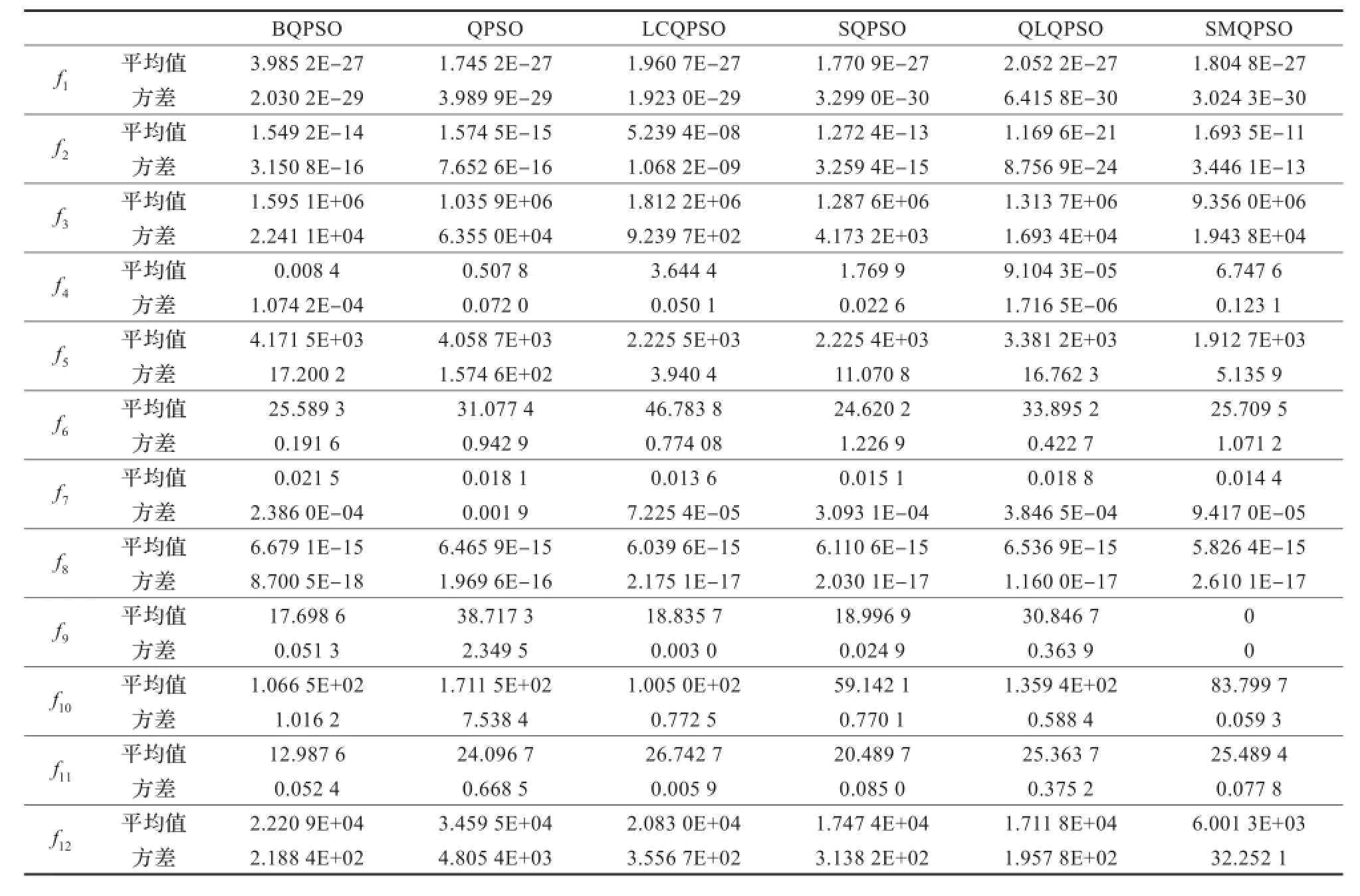
表2　SMQPSO与BQPSO、QPSO、LCQPSO、SQPSO和QLQPSO运行50轮后的平均最优值及方差

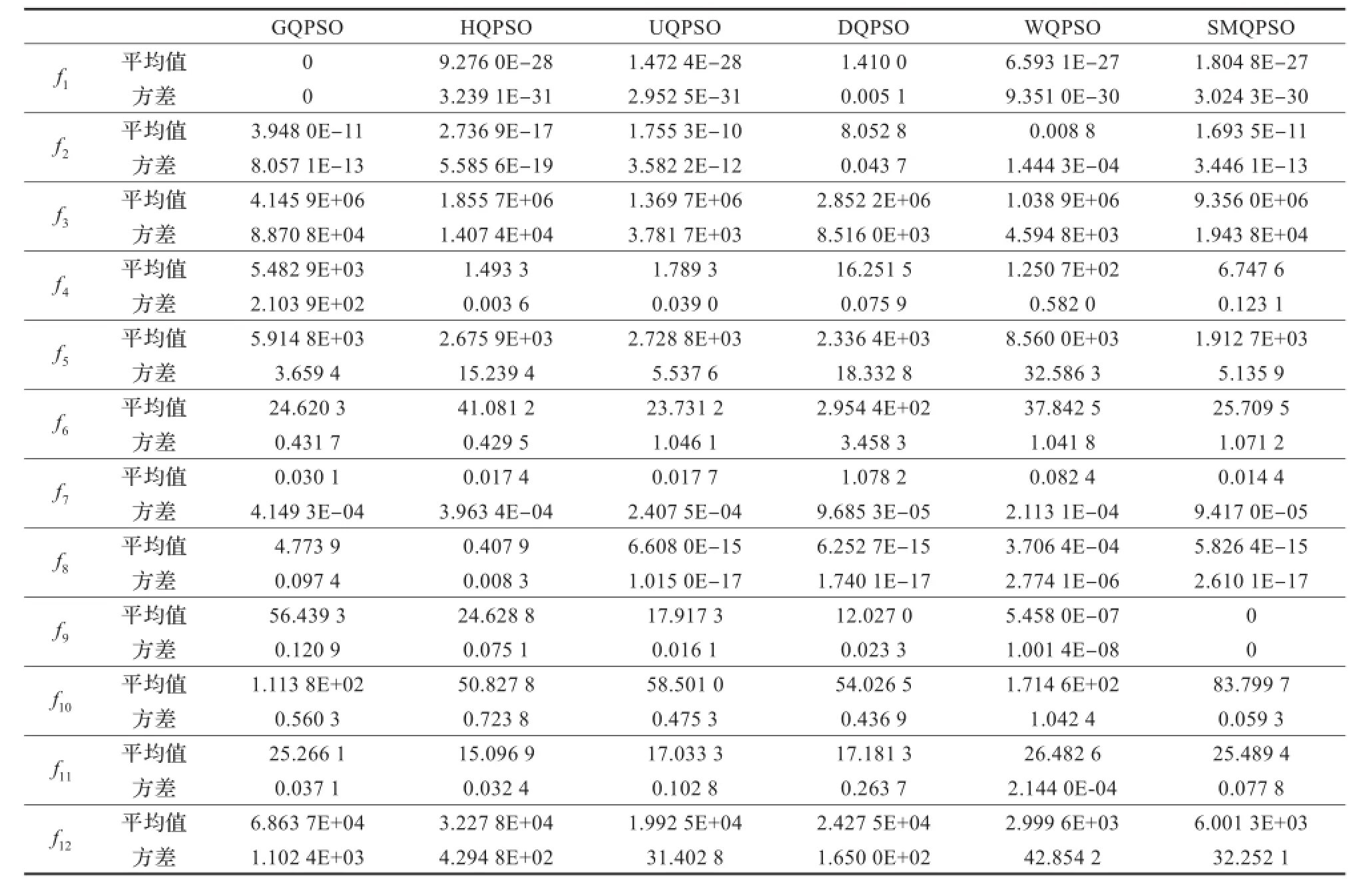
表3　SMQPSO与GQPSO、HPSO、UQPSO、DQPSO和WQPSO运行50轮后的平均最优值及方差

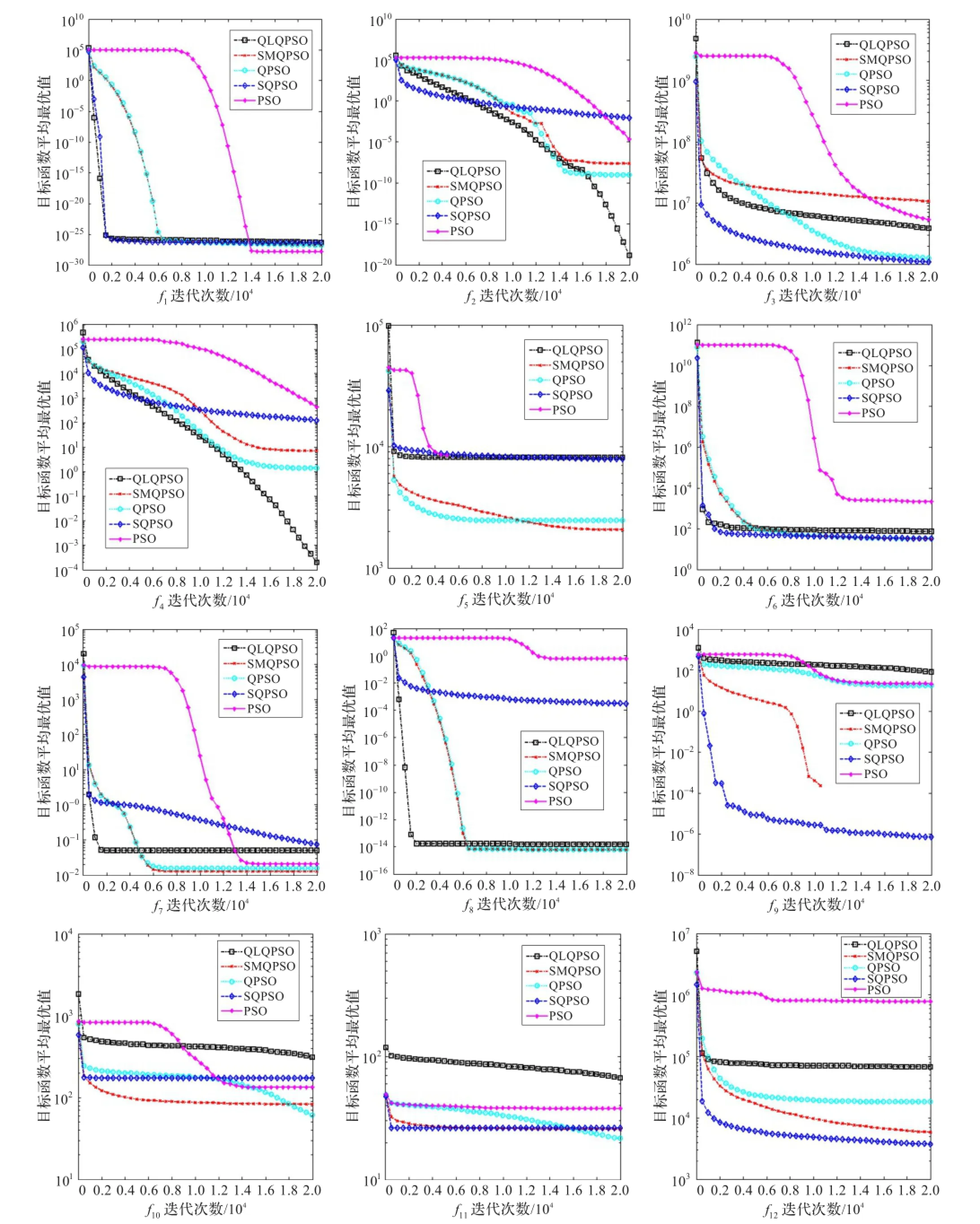
图5　不同算法优化测试函数时的目标函数值收敛曲线比较

为了更好地比较测试算法整体性能，本文使用了ANOVA测试方法［17］研究各个改进算法的整体性能，其中ANOVA测试方法中显著性水平数值设置为0.05。所有算法根据测试结果排序决定对测试问题是否是可靠有效。表4给出了各个算法对于12个测试函数的排序结果，表5给出了专门针对多峰问题（f6～f12）7个测试函数的排序结果。从表4中的排序值看出，SQPSO算法的排序值为49，对于12个测试函数整体性能最优，UQPSO算法和SMQPSO算分别以排序中56、57紧随其后。而对于较难寻优的7个多峰问题，本文提出的SMQPSO算法排序值为25，在所有算法中性能最优。这些数值比较显示，带有自我更新机制的QPSO算法在测试函数优化中增加了群体多样性，表现出较强的寻优特性，尤其是在多峰问题中能够迅速的搜索到最优值。

表4　不同算法优化12个测试函数时的性能比较表

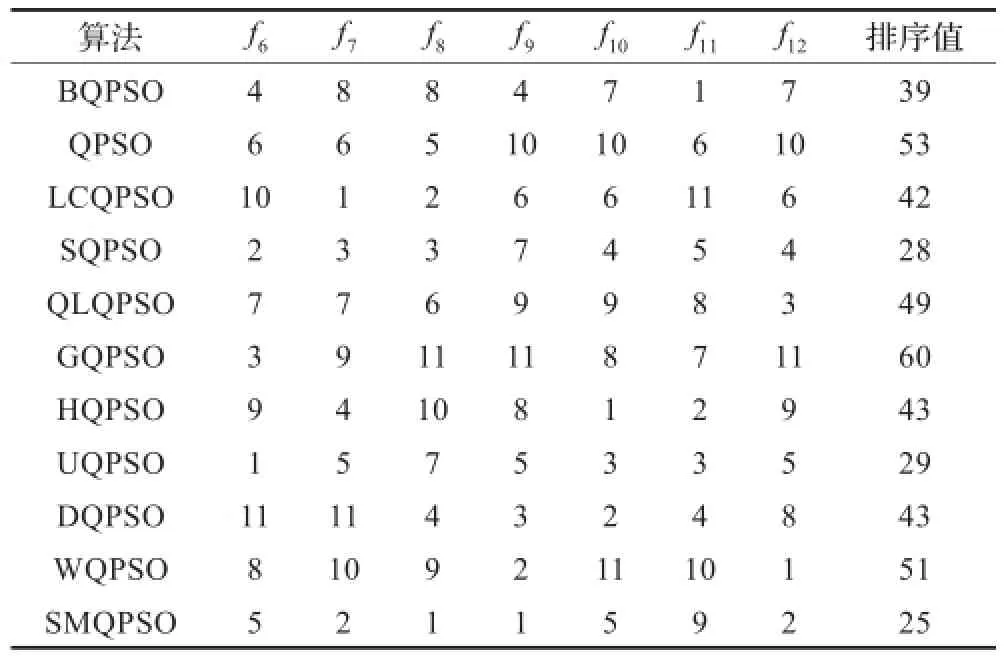
表5　不同算法优化7个多峰函数时的性能比较表

6　结束语

分析了QPSO算法的进化方程，研究了自然界中生命体进化时，随着时间的推移存在老化并死亡的现象。在QPSO算法进化过程中，引入了自我更新机制，提出了领导者粒子和挑战者粒子概念，通过当前群体粒子表现来计算领导者粒子的领导力，分析了不同状态下的领导力计算方法，当领导力耗尽时，通过挑战机制判断领导者粒子是否需要更新，并给出了整个算法的执行过程。具有自我更新机制的QPSO算法充分保持了群体进化过程中的多样性，在使用CEC2005测试函数和其他几种不同改进算法的仿真比较中，结果显示具有自我更新机制的QPSO算法在大部分测试函数上能够取得更优的结果，尤其在多峰测试上更加明显，其他函数也能够取得和其他方法相近的结果，因此SMQPSO算法能够提高QPSO算法的整体性能。

［1］Kennedy J，Eberhart R.Particle swarm optimization［C］// Proceedings of IEEE International Conference on Neural Network.Perth，WA：IEEE，1995：1942-1948.

［2］Van Den Bergh F.An analysis of particle swarm optimizers［D］. Pretoria：University of Pretoria，2001.

［3］Chen W，Zhang J，Lin Y，et al.Particle swarm optimization with an aging leader and challengers［J］.IEEE Transactions on Evolutionary Computation，2013，17（2）：241-258.

［4］Campos M，Krohling R，Enriquez I.Bare bone particle swarm optimization with scale matrix adaption［J］.IEEE Transactions on Cybernetics，2014，44（9）：1567-1578.

［5］Sun J，Xu W，Feng B.A global search strategy of quantumbehaved particle swarm optimization［C］//Cybernetics and Intelligent Systems，Proceedings of the 2004 IEEE Conference.Sigorpore：IEEE，2004：111-116.

［6］Sun J，Xu W，Plade V，et al.Convergence analysis and improvements of quantum-behaved particle swarm optimization［J］.Information Sciences，2012，193：81-103.［7］Xi M，Sun J，Xu W.An improved quantum-behaved particle swarm optimization algorithm with weighted mean best position［J］.Applied Mathematics and Computation，2008，205（2）：751-759.

［8］Sun J，Fang W，Xu W，et al.Quantum-behaved particle swarm optimization analysis of individual particle behavior and parameterselection［J］.EvolutionaryComputation，2012，20（3）.

［9］Fang W，Sun J，Xu W，et al.Analysis of mutation operators on quantum-behaved particle swarm optimization algorithm［J］. Mathematics and Natural Computation，2009，5（2）：487-496.

［10］Omkar S，Khandelwal R，Ananth T，et al.Quantum behaved Particle Swarm Optimization（QPSO）for multi-objective designoptimizationofcompositestructures［J］.Expert Systems with Applications，2009，36（8）：11312-11322.

［11］Indiral K，Kanmani S，Jagan R，et al.An evolutionary quantum behaved particle swarm optimization for mining associationrules［J］.InternationalJournalofScientific &Engineering Research，2014，5（5）：379-388.

［12］Farzi S，Shavazi A，Pandari A.Using quantum-behaved particle swarm optimization for portfolio selection problem［J］. The International Arab Journal of Information Technology，2013，10（2）：111-119.

［13］Clerc M，Kennedy J.The particle swarm：explosion，stability and convergence in a multi-dimensional complex space［J］. IEEE Transactions on Evolutionary Computation，2002，6：58-73.

［14］Suganthan P，Hansen N，Liang J，et al.Problem definitions and evaluation criteria for the CEC 2005 special session onreal-parameteroptimization［R］.Singapore：Nanyang Technological University，2005.

［15］Solis F，Wets R.Minimization by random search techniques［J］.Mathematics of Operations Research，1981，6（1）：19-30.

［16］Fang W.Swarm intelligence and its application in the optimal design of digital filters［D］.Wuxi：Jiangnan University，2008.

［17］Day R，Quinn G.Comparisons of treatments after an analysis of variance in ecology［J］.Ecological Monographs，1989，59：433-463.

［18］Sheng X，Xi M，Sun J，et al.Quantum-behaved particle swarmoptimizationwithnoveladaptivestrategies［J］. Journal of Algorithms&Computational Technology，2015，9（2）：143-161.

Quantum-behaved Particle Swarm Optimization algorithm with self-renewal mechanism.

XI Maolong1，2，WU Xiaojun2，FANG Wei2，SUN Jun2

1.School of Control Technology，Wuxi Institute of Technology，Wuxi，Jiangsu 214121，China
2.School of Internet of Things，Jiangnan University，Wuxi，Jiangsu 214122，China

Life body has limited life in nature；it will be aging and die with time.The aging mechanism is very important to keep swarm diversity during evolutionary process.For the phenomenon that Quantum-behaved Particle Swarm Optimization（QPSO）is often premature convergence，self-renewal mechanism is proposed into QPSO，and a leading particle and challengers are introduced.When the leading power of leading particle is exhausted，one challenger will select to be the new leading particle and continues keeping the diversity of swarm with a certain renewal mechanism.Furthermore，global convergence of the proposed algorithm is proved.Finally，the comparison and analysis of results with the proposed method and classical improved QPSO algorithm based on twelve CEC2005 benchmark function is given，the simulation results show stronger global searching ability of the modified algorithm.Especially in the seven multi-model test functions，the comprehensive performance is optimal.

PSO algorithm；quantum behaved；self-renewal mechanism；diversity；global convergence；aging

A

TP301.6

10.3778/j.issn.1002-8331.1509-0064

国家自然科学基金（No.61170119）；江苏省“青蓝工程”学术带头人培养对象资助。

奚茂龙（1977—），男，副教授，博士后，主要研究方向为智能优化算法及应用；吴小俊（1967—），男，教授，博士生导师，主要研究方向为模式识别与人工智能；方伟（1981—），男，副教授，博士，主要研究方向为群体智能与进化计算；孙俊（1971—），男，教授，博士，主要研究方向为人工智能、算法设计。E-mail：wx_xml@hotmail.com

2015-09-04

2015-10-13

1002-8331（2015）22-0001-09