悬带扭力零位引起的陀螺经纬仪定向误差分析

田育民,刘思伟

1.西安测绘研究所，陕西 西安，710054；2.地理信息工程国家重点实验室，陕西 西安，710054



悬带扭力零位引起的陀螺经纬仪定向误差分析

田育民1,2,刘思伟1,2

1.西安测绘研究所，陕西 西安，710054；2.地理信息工程国家重点实验室，陕西 西安，710054

悬带扭力零位稳定性对于摆式陀螺寻北仪的研制至关重要。本文介绍了摆式陀螺寻北工作原理，讨论了陀螺主轴扭摆平衡位置、悬带扭力零位和真北方向三者之间的关系；在此基础上，依据积分测量观测方法，分析了悬带扭力零位稳定性对陀螺经纬仪定向误差的影响，并利用TS09陀螺经纬仪的实测数据对理论分析进行验证。理论分析和试验结果表明，通过提高悬带扭力零位稳定性，可进一步提高国产陀螺经纬仪的定向精度。

陀螺经纬仪；悬带扭力零位；积分法；定向精度

1　引　言

陀螺经纬仪是一种精密的测量真北仪器，广泛应用于测绘、矿山、隧道、军事、航空和航天等领域。陀螺经纬仪中的陀螺寻北技术主要以定向精度较高的摆式陀螺寻北技术为主[1，2]。影响摆式陀螺寻北精度和稳定性的成因复杂，内因主要包括陀螺电机转速稳定性、自摆零位稳定性、悬带弹性质量稳定性、磁屏蔽质量稳定性等；外因主要有环境温度、地理纬度、地面振动等。这些复杂的内外因素降低了陀螺经纬仪的定向精度。

陀螺经纬仪定向误差包括一次定向中误差和仪器常数漂移两项误差，是评价陀螺经纬仪性能的重要指标之一[3，4]。目前，国产陀螺经纬仪出厂标称精度以中误差表示，大多在“角秒级”，一般不涉及仪器常数漂移。因为国产陀螺经纬仪仪器常数长期漂移远大于标称精度，所以陀螺经纬仪实际使用前必须进行仪器常数标定工作，造成陀螺经纬仪推广使用受到或多或少的限制。陀螺经纬仪长期稳定性差表现为仪器常数漂移较大，测量过程中的不稳定表现为仪器中误差值较大。GYRMAT3000是目前定向精度最高、稳定性能最好的陀螺经纬仪，其定向精度小于1mgon(约3.24″),仪器常数年漂移小于±0.002gon(约±6.48″)。当前国产陀螺经纬仪稳定性的研究主要针对仪器常数的漂移问题[5，6]，较少研究短期稳定性对测量中误差的影响。为了提高国产陀螺经纬仪测量数据的可靠性，本文在介绍摆式陀螺寻北工作原理，以及陀螺主轴扭摆平衡位置、悬带扭力零位和真北方向三者关系的基础上，依据积分测量观测法原理，分析了陀螺寻北积分法中陀螺仪扭力零位对陀螺经纬仪定向误差的影响，并结合实验数据进行了验证。理论分析和试验结果表明，要提高摆式陀螺经纬仪的定向精度，必须解决悬带扭力零位稳定性问题。

2　陀螺寻北系统工作原理

摆式陀螺寻北仪工作原理如图1所示，其主要部件包括陀螺敏感部和光电转换系统。陀螺敏感部由陀螺电机、陀螺房体、悬挂带、摆镜等组成。陀螺电机是一个外转子电机，通过外转子电机自转轴安装在陀螺房体中，陀螺房体通过悬挂带固定在仪器外壳体上，摆镜与陀螺房体固连。陀螺仪寻北工作时，摆镜随陀螺房体一起扭摆。光电转换系统由线光源、光路、光电位置传感器等组成。光电转换系统与仪器外壳固连，仪器工作时静止不动，线光源发出的光束经棱镜、反射镜、透镜等组成的光路照射到摆镜上，经摆镜反射后成像于光电位置传感器上。这样，陀螺仪的扭摆信息就可以通过光电位置传感器上成像的光斑运动反映出来。

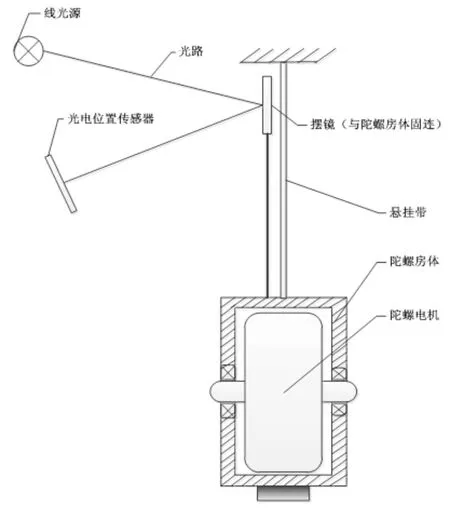
图1　摆式陀螺寻北仪工作原理示意图

当陀螺电机自转轴(以下简称陀螺主轴)不在当地子午面内时，由于重力矩的作用，地球自转引起的陀螺主轴倾斜使得陀螺主轴向当地子午面进动。当陀螺主轴进动至当地子午面时，地球自转对陀螺主轴不再产生影响，陀螺主轴位于当地子午面内且平行于当地地平面，此时，理论上讲陀螺主轴应保持空间方位不变。但是，由于陀螺主轴进动的惯性作用，陀螺主轴会穿越当地子午面继续运动。一旦陀螺主轴偏离当地子午面，地球自转又会对陀螺主轴产生一个重力矩，迫使陀螺主轴向当地子午面进动，造成陀螺主轴围绕当地子午线面来回扭摆，其扭摆的平衡位置即为当地子午线方向。摆式陀螺仪寻北就是通过测定陀螺主轴扭摆的平衡位置确定真北方向。

3　悬带扭力零位对定向误差的影响分析

自动陀螺寻北仪中，为了测定陀螺主轴扭摆的平衡位置，必须将陀螺主轴的扭摆运动转换为电信号。如图1所示，陀螺仪寻北时，陀螺主轴围绕当地子午面来回扭摆，造成与陀螺房体固连的摆镜沿铅锤方向来回扭摆，摆镜的来回扭动引起摆镜光路在光电位置传感器上的光斑围绕一个中心点来回运动。理想条件下，陀螺主轴末端的运动轨迹是一条椭圆曲线，反映在光电位置传感器上的光斑轨迹是正弦曲线或衰减的正弦曲线[7]，陀螺仪寻北的很多观测方法都是以此为依据推导出的。但是，陀螺主轴末端运动轨迹的精确数学模型很难求得，或者由于精确的数学模型过于繁琐，实际的陀螺寻北方法往往通过实践进行简化。

假设陀螺主轴的扭摆平衡位置为R，R是在悬带弹性扭力矩与陀螺力矩的共同作用下产生的。这样，陀螺主轴扭摆平衡位置R、悬带扭力零位B和真北方向N的三者关系如图2所示。

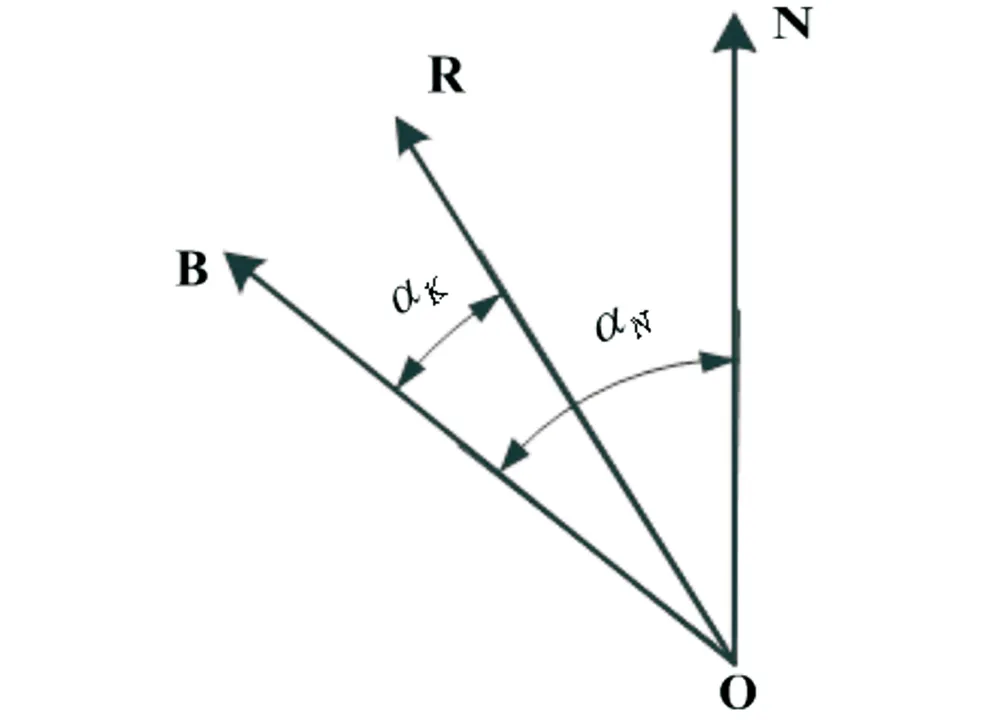
图2　陀螺主轴扭摆平衡位置与真北之间关系图

依据三者的关系，力矩平衡方程为：

αKDB=(αN-αK)DK

(1)

式中，αK为悬带扭力零位与陀螺主轴的扭摆平衡位置之间的夹角；DB为悬带的扭力矩；αN为悬带扭力零位与真北方向之间的夹角；DK为陀螺力矩。

陀螺力矩DK与陀螺电机的角动量H、测站纬度φ以及地球自转角速度ωe之间的关系如下：

DK=Hωecosφ

(2)

αN=αK(1+K)

(3)

由式(3)可以看出，已知K和αK，即可推算出真方位角。K值通过理论推算很难得出结果，通常将陀螺经纬仪架设在已知方位边的测站上，通过实测数据推算；αK可通过中天法、时差法、逆转点法、积分法的方法观测得出[8-10]。

本文通过积分观测方法求取αK。将陀螺主轴围绕当地子午面来回运动引起光电位置传感器上光斑的运动轨迹看成接近于简谐振荡运动，如图3所示。图中，t为时间轴，x为位置轴，坐标原点0在位置轴x上表示光电位置传感器上的一个端点，x(t)表示摆镜光路光斑在光电位置传感器上的运动轨迹，T为简谐振荡周期，R为摆镜光路光斑在光电位置传感器上运动轨迹的中心点，B为陀螺仪悬带扭力为零时摆镜光路光斑在光电位置传感器上的投影点。陀螺寻北积分法就是连续采集光电位置传感器输出的电信号，通过确定光电位置传感器上光斑运动的中心点R，达到陀螺仪寻北目的的一种观测方法。

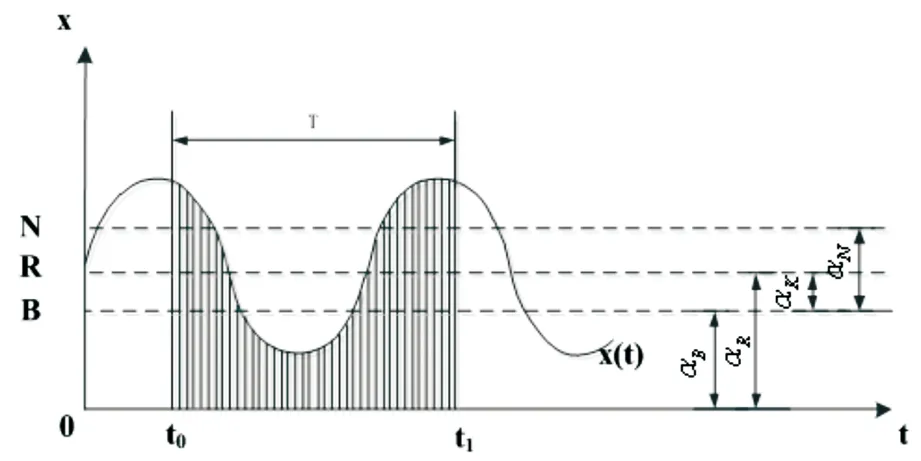
图3　积分原理图

由图3描述的各种关系，可将式(3)变换为：

αN=αK(1+K)=(αR-αB)(1+K)

(4)

假设陀螺经纬仪度盘为零时，摆镜光路光斑在光电位置传感器上的投影点处于x坐标轴0点。式(4)中，αB代表悬带扭力零位与度盘零位之间的夹角，αR代表陀螺主轴扭摆平衡位置与度盘零位之间的夹角，αN+αB表示真北方向与读盘零位之间的夹角。在已知真北方向与读盘零位之间夹角的情况下，则可以通过经纬仪测量任意目标的方位角。

假设悬带扭力零位测量误差为ΔαB，悬带扭力零位测量误差引起的摆式陀螺经纬仪定向误差为(K+1)ΔαB。由此可见，悬带扭力零位的稳定性直接影响摆式陀螺经纬仪的定向精度，一测回中悬带扭力零位的稳定性直接影响陀螺定向测量值，悬带扭力零位的长期稳定性直接影响陀螺经纬仪仪器常数的稳定性。

4　算例分析

为了进一步说明摆式陀螺悬带扭力零位稳定性对定向精度的影响，本文利用TS09陀螺经纬仪测量数据进行分析。测量数据包括6组测量结果，每组测量包含9次测量，测量数据如表1所示，表1中的每组测量数据为9次测量值的平均值。

表1TS09陀螺经纬仪测量数据

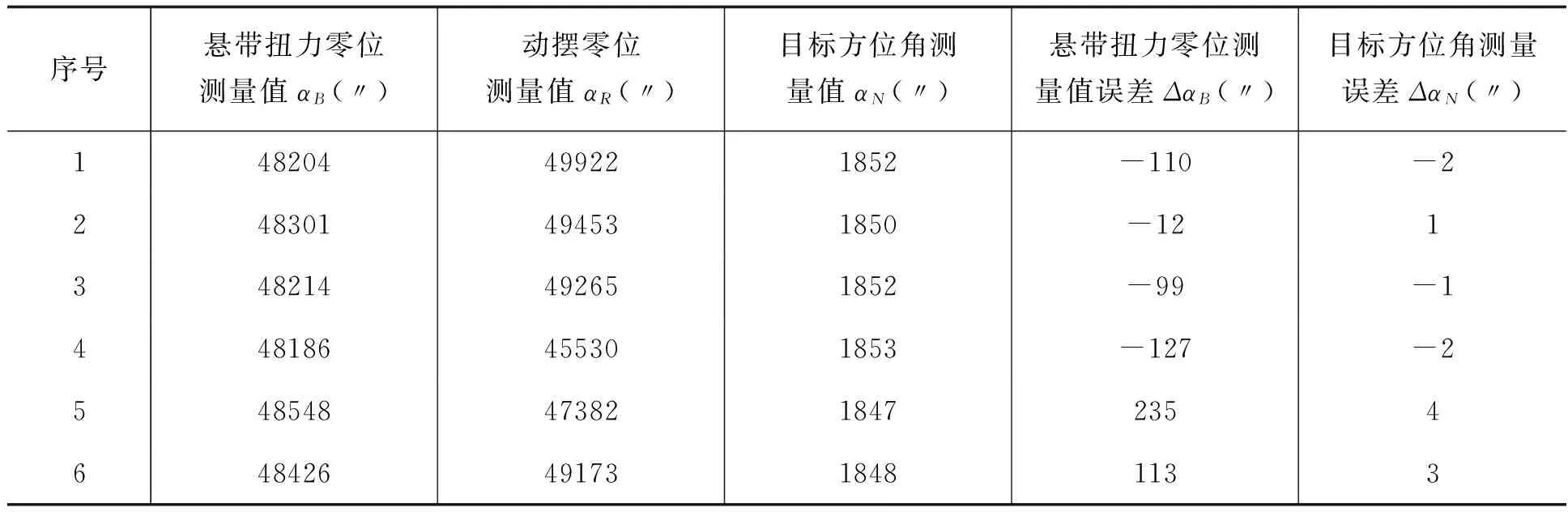
序号悬带扭力零位测量值αB(〃)动摆零位测量值αR(〃)目标方位角测量值αN(〃)悬带扭力零位测量值误差ΔαB(〃)目标方位角测量误差ΔαN(〃)148204499221852-110-2248301494531850-121348214492651852-99-1448186455301853-127-254854847382184723546484264917318481133

为了直观分析摆式陀螺悬带扭力零位稳定性对定向精度的影响，将6组测量数据中悬带扭力零位误差作为横坐标，方位角测量误差作为纵坐标，悬带扭力零位误差与目标方位角测量误差之间的关系如图4所示。从图中可以看出，悬带扭力零位误差与定向误差之间的关系与理论分析相符。

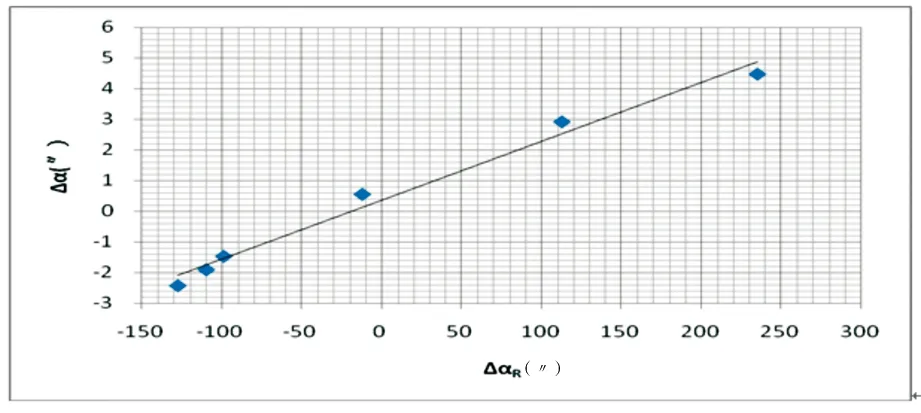
图4　悬带扭力零位测量值误差与定向误差关系

5　结　论

摆式陀螺经纬仪悬带扭力零位稳定性对定向精度有着直接影响，测量过程中悬带扭力零位稳定性影响陀螺经纬仪测量值，长期稳定性造成仪器常数漂移。为了提高陀螺经纬仪的定向精度，一方面从仪器硬件着手，提高悬带固定的牢靠性、光学系统和光电转换电路的稳定性等；另一方面改进测量软件，达到提高定向精度的目的。对TS09陀螺经纬仪测量数据的分析表明，如果进一步改进测量算法，TS09陀螺经纬仪则具有提高定向精度的潜力。

[1]许其凤，丛佃伟，董明. 主要定向技术比较与GNSS快速定位定向仪研制进展[J]. 测绘科学技术学报，2013，30(4)：349-352.

[2]田育民，刘思伟，白云超. 摆式陀螺经纬仪粗寻北的方法[J]. 中国惯性技术学报，2009，17(4)：441-443.

[3]秦洪奎. 陀螺经纬仪定向精度的研究[J]. 测绘信息与工程，2009，34(3)：49-51.

[4]王庆林. 陀螺经纬仪定向系统误差研究[J]. 测绘科学，2010，35(5)：56-58.

[5]王飞，邓向瑞，李广云等. 陀螺经纬仪的仪器常数随温度漂移规律的研究[J]. 武汉大学学报，2011，36(3)：289-292.

[6]蒋庆仙, 陈晓璧, 马小辉. 陀螺经纬仪的仪器常数及其测定[J]. 测绘科学，2008，33(2)：152-154.

[7]林玉池，孙占元，赵美蓉等．中天法在陀螺智能寻北系统中的应用研究[J]. 机械工程学报，2003，39(8)：116-119.

[8]周召发，常振军，张志利. 摆式陀螺寻北仪快速寻北的时差逆转点法[J]. 探测与控制学报，2012，34(4)：64-66.

[9]王缜，申功勋. 摆式陀螺寻北仪的积分测量方法[J]. 光学精密工程，2007，15(5)：746-752.

[10]林明春，夏桂锁，林玉池等. 积分法在智能陀螺寻北系统中的应用研究[J]. 传感器与微系统，2007，26(10)：57-59.

Analysis of Orientation Error Induced by Tensional Zero Position in a Gyro theodolite

Tian Yumin1,2,Liu Siwei1,2

1.Xi’an Research Institute of Surveying and Mapping, Xi’an 710054, China 2.State Key Laboratory of Geo-information Engineering, Xi’an 710054, China

The stability of tensional zero position is crucial in a pendulous gyro theodolite. This paper introduces the north seeking principle of pendulous gyroscope and discusses the relation between equilibrium position of gyro-swing, tensional zero position and true north direction. Besides the paper analyzes the influence of stability of tensional zero position on orientation error based on integral measuring method, which is proved by the measured data of TS09 gyro theodolite. The results show that the orientation accuracy of home gyro theodolite can be improved by enhancing stability of tensional zero position.

gyro theodolite; tensional zero position; integral method; orientation accuracy

2015-06-05。

田育民(1964—)，男，高级工程师，主要从事惯性测量研究。

V241.5

A