基于平行基线的机载InSAR直接相位解缠方法

刘志铭，楼良盛，张笑微

1.信息工程大学地理空间信息学院，河南 郑州，450052；2.西安测绘研究所，陕西 西安，710054；3.地理信息工程国家重点实验室，陕西 西安，710054



基于平行基线的机载InSAR直接相位解缠方法

刘志铭1，2，3，楼良盛2，3，张笑微2，3

1.信息工程大学地理空间信息学院，河南 郑州，450052；2.西安测绘研究所，陕西 西安，710054；3.地理信息工程国家重点实验室，陕西 西安，710054

本文通过分析机载InSAR干涉相位特点，提出平行基线可以近似代替主辅影像斜距差，因此利用平行基线不仅可以解算绝对相位，而且可以直接完成相位解缠而不会引入额外误差，为机载InSAR相位解缠提供了新的解决方案，有效避免了已有机载InSAR相位解缠算法的缺陷。为了验证该方案的可行性，本文利用机载真实数据进行了相位解缠试验，结果表明，利用平行基线直接相位解缠是完全可行的。

平行基线；InSAR；相位解缠

1　引　言

相位解缠一直是机载InSAR数据处理的难点，也是多年来研究的热点。目前常用的相位解缠算法包括：枝切法(Branch-cut法)、Flynn的最小不连续法、区域生长法、最小LP范数法、最小费用流算法等[1-4]。这些算法均是基于干涉条纹图自身的特点，从图像处理的角度来恢复被缠绕的相位，而并没有从机载InSAR原理出发，从成像的角度来解决机载InSAR相位解缠的难题，均未有最佳的相位解缠解决方案。根据目前相位解缠算法分类，基于路径跟踪的相位解缠算法在强噪声情况下，容易造成误差传递或无法解缠的孤立区域；基于最小范数的相位解缠算法容易造成误差传递；基于最优估计的相位解缠算法将相位解缠问题转化为病态方程求解问题，获取相位解缠的最优解，计算量非常大；基于特征提取的相位解缠方法要求条纹间隔必须清晰，干涉条纹边缘必须连续。同时，目前的相位解缠算法只能解决针对图幅中某一点的相对相位解缠，而具体到每个像元还存在一个绝对相位2nπ需要确定。本文从机载InSAR成像理论出发，分析了平行基线与主辅影像斜距差之间的差异，提出了利用平行基线代替主辅影像斜距差进行相位解缠的处理方案，不仅可以完成相位解缠，而且可以直接得到绝对相位，同时，不需要探测噪声点和残差点，也不会引入额外的解缠误差，具有较好的鲁棒性。本文最后利用机载真实InSAR数据，对该方案的可行性进行了验证。

2　基本原理

机载InSAR由于受飞机平台限制，有效基线长度不可能太长，因此主辅雷达天线一般采用刚性连接，基线长度和基线倾角在地面采用静态测量方法获取，这为计算平行基线提供了输入条件。

2.1机载InSAR干涉相位与平行基线关系分析

根据机载InSAR成像原理[6]，主辅雷达天线相位中心与地面点的关系如图 1所示，其中A1、A2分别为主辅雷达，R1、R2分别为主辅雷达与地面点P间斜距，B和α分别为基线长度和基线倾角，θ为侧视角，H为飞机航摄高度。

图1　InSAR成像斜距差计算示意图

根据图1，可以写出：

(1)

其中，φ为绝对相位差，λ为波长。

φ=n·2π+φ0

(2)

其中，φ0为干涉相位，n为模糊数。

机载InSAR的基本原理就是利用干涉相位计算目标点与主辅雷达天线距离差，相反，只要能计算出ΔR，就可以通过公式(2)获取干涉相位差以及模糊数n。

从图1可以看出，辅雷达斜距R2可表示为：

(3)

整理可得：

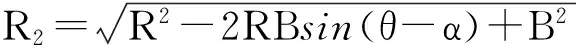
即R2≥R-Bsin(θ-α)，

故ΔR=R-R2≤Bsin(θ-α)

(4)

由于R≫B，因此R2受R的影响要远大于受B影响，故Bsin(θ-α)接近ΔR。

现在考察利用Bsin(θ-α)代替ΔR的可行性。假定机载InSAR基线长度为4m，最小侧视角为20°，航高为8000m，基线倾角为40°，则：

Bsin(θ-α)-ΔR=0.0008296m

(5)

由于X波段波长为3cm，Ku波段波长为1.9cm，因此无论是X波段还是Ku波段，利用Bsin(θ-α)代替ΔR均不会改变2nπ的值。事实上，机载InSAR基线长度一般会小于4m，因此这两者之间的差值会更小。

因此，对于机载InSAR数据处理，当平行基线Bsin(θ-α)能够准确获取时， 可以利用平行基线来计算模糊数n，而不需要地面控制点。

2.2侧视角估计误差影响分析

计算平行基线公式中唯一不确定的因子是侧视角θ，因为侧视角随地形起伏是不断变化的，因此有必要分析地形起伏引起侧视角的变化大小。

首先分析地形起伏对相邻像元侧视角差异的影响。假定航高8000m，近距边侧视角20°，距离向10000个像元，斜距分辨率0.5m，迎坡10°、25°和背坡10°、25°相邻像元侧视角差的变化情况如图 2所示；若斜距分辨率为1m，迎坡10°、25°和背坡10°、25°相邻像元侧视角差的变化情况如图 3所示。

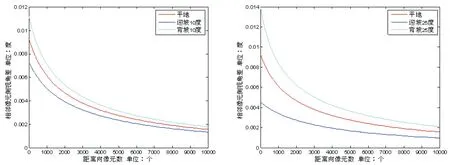
a.坡度10°时相邻像元侧视角差的变化 b.坡度25°时相邻像元侧视角差的变化图2　分辨率0.5m时相邻像元侧视角差的变化情况

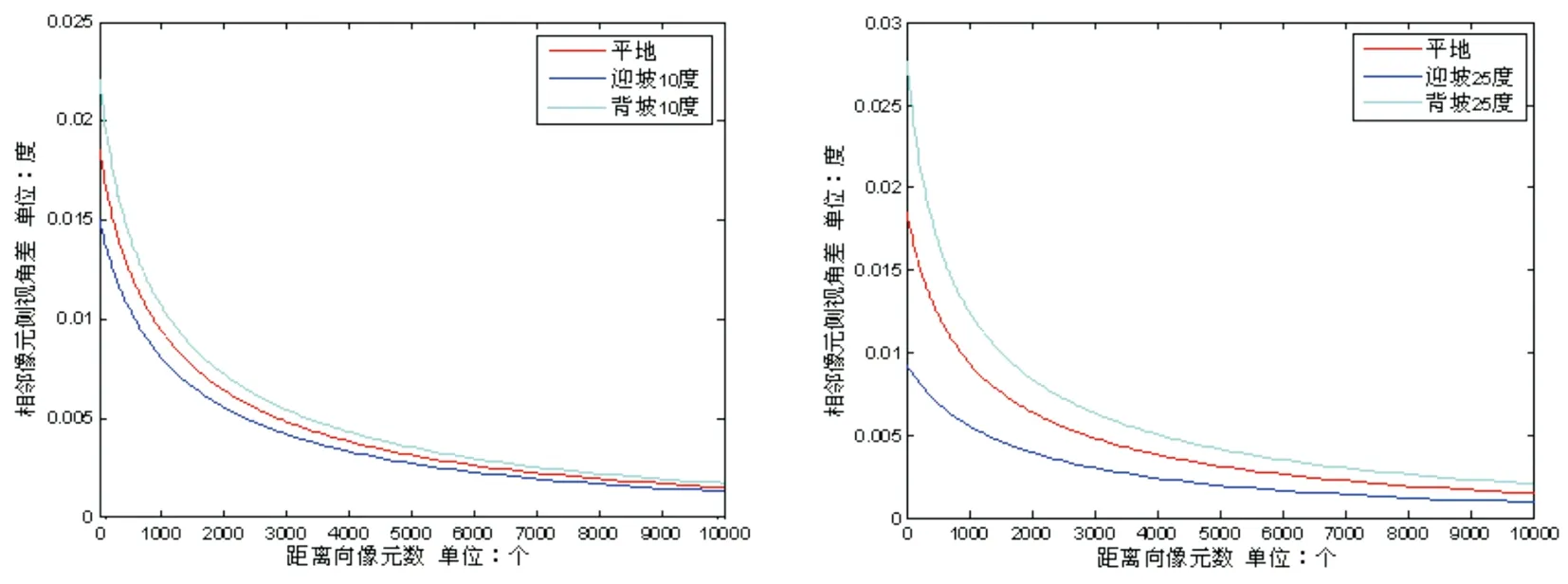
a.坡度10°时相邻像元侧视角差的变化 b.坡度25°时相邻像元侧视角差的变化图3　分辨率1m时相邻像元侧视角差的变化情况

从图 2、图 3中可以看出，相对于平地，地面坡度25°以内的相邻像元侧视角差的较差最大不会超过0.01°，并且最大较差发生在近距端，同时沿距离向逐渐变小。假定机载InSAR基线长度为4m，则由地形起伏引起的平行基线误差为0.0007m，对于X波段和Ku波段来讲，估计2nπ均没有影响。因此，可以利用平均高程计算的相邻像元侧视角差代替真实地形相邻像元侧视角差。

其次分析地形起伏对侧视角估计精度的影响。由于雷达采用斜距成像，侧视角与像元位置没有严密公式，但是沿距离向像元位置的变化在一定程度上也能反映出侧视角的变化，而受地形起伏的影响，实际像元位置会偏离平地计算出的位置，因此，直接利用地面平均高程估算侧视角会产生较大误差。为了提高侧视角估计精度，可利用平均高程估计出的侧视角计算平行基线，利用平行基线获得平地干涉相位图，通过与真实干涉条纹比较，得到近距端干涉条纹像元偏移量，进而估算出侧视角差异；通过调整侧视角大小，使得整幅影像近距端干涉条纹像元偏移量均在1/4个条纹宽度内，即估计出的干涉相位差不会超过π/2，使得侧视角的估计精度满足相位解缠要求，如果不能满足此条件，则需要沿方位向进行分块处理。

因此侧视角的估计需首先估计出近距端侧视角的大小，利用计算出的平行基线对近距端像元进行解缠，然后根据解缠相位计算出真实侧视角，接着利用平地相邻像元侧视角差估计下一点的侧视角，对下一点进行相位解缠和真实侧视角计算。如此反复，直至距离向最远端像元完成相位解缠，从而有效克服地形起伏对侧视角估计精度的影响。

2.3基于平行基线相位解缠的基本思路

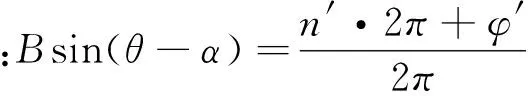
因此给出如下判据：

(1)当φ′+φ0<π/2时，n=n′-1，即φ=(n′-1)·2π+φ0；

(2)当φ′+φ0<(3π-π/2)时，n=n′，即φ=n′·2π+φ0；

(3)当φ′+φ0≥(3π-π/2)时，n=n′+1，即φ=(n′+1)·2π+φ0；

说明：在实际解算过程中，φ′的取值范围为[0,2π)，而利用三角函数直接解算的φ0的取值范围为(-π,π)，因此，利用上述判据前需要将φ0变为φ0+π。

通过逐点解算，即可完成整幅影像的相位解缠，并且该模糊数n是绝对的，解缠相位可以直接用于后续的DEM生成。

3　实验与分析

为了验证该方案的可行性，本文利用2005年9月西安测绘研究所和中科院电子所联合获取的机载InSAR试验数据，进行了相位解缠试验。机载InSAR试验数据技术参数如表1所示。

表1机载InSAR试验数据部分技术参数

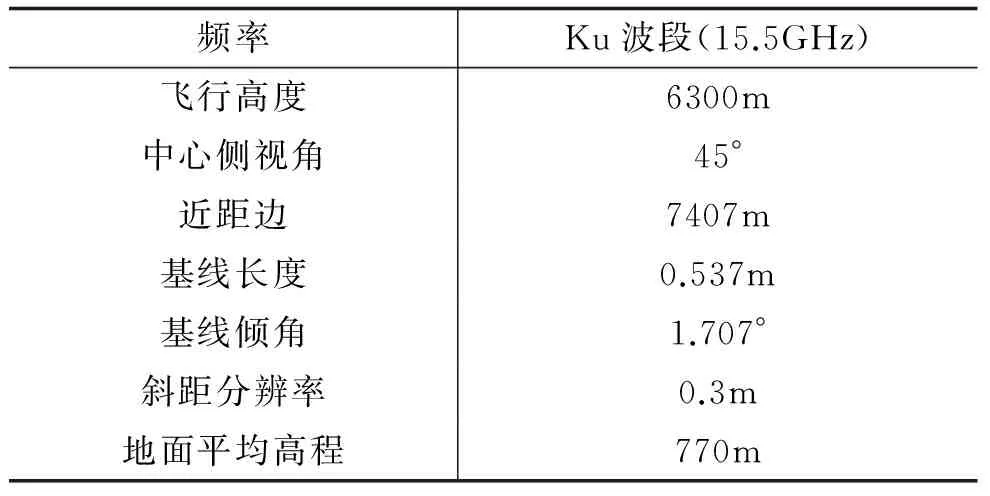
频率Ku波段(15.5GHz)飞行高度6300m中心侧视角45°近距边7407m基线长度0.537m基线倾角1.707°斜距分辨率0.3m地面平均高程770m

根据计算的平行基线，利用上节判据，进行了直接相位解缠，近距端模糊数为18，远距端模糊数为21，干涉条纹图与相位解缠图如图 4所示。

a.干涉条纹图 b.相位解缠图图4　直接相位解缠对照图

从干涉条纹图中可以看出，相位噪声相当严重，如果不采用掩膜加权或隔离，直接进行解缠，传统的方法是很难成功的，而本文解缠算法不受噪声的影响，可以对非噪声点进行正确解缠，并且不需要探测噪声点和残差点，也不会引入额外的解缠误差，因此，有效提高了机载InSAR相位解缠的鲁棒性。

4　结　论

本文首先从理论上分析了利用平行基线进行机载InSAR相位解缠的可行性，又从操作层面上给出了相位解缠的判据，最后利用机载真实数据验证了方案的有效性。结果表明，利用平行基线进行机载InSAR相位解缠，无论是理论上还是实践中均是可行的，为机载InSAR相位解缠提供了一个全新的处理手段。

[1]许才军，王华．InSAR相位解缠算法比较及误差分析[J]．武汉大学学报(信息科学版)， 2004(1):67-71.

[2]刘志铭．干涉合成孔径雷达相位解缠算法的研究[D]．郑州：信息工程大学，2004.

[3]肖枫．InSAR相位解缠算法的研究[D]．上海：同济大学，2008.

[4]黄蓉．InSAR相位解缠算法比较研究[D]．西安：长安大学，2012.

[5]王超，张红，刘智．星载合成孔径雷达干涉测量[M]．北京：科学出版社，2002.

A Direct Phase Unwrapping Method for Airborne InSAR System Based on Parallel Baseline

Liu Zhiming1,2,3, Lou Liangsheng2,3, Zhang Xiaowei2,3

1.Institute of Geospatial Information,Information Engineering University,Zhengzhou 450052,China 2.Xi’an Research Institute of Surveying and Mapping,Xi’an 710054,China 3.State Key Laboratory of Geo-information Engineering,Xi’an 710054,China

Based on the analysis of interferometry phase of airborne InSAR system, the parallel baseline is considered to be an acceptable substitute for the slant range difference. Since the parallel baseline can be used to solve absolute phase and avoid extra error in phase unwrapping, a novel solution to airborne InSAR phase unwrapping is presented. Real airborne InSAR data is employed to testify the feasibility of the solution, and the result indicates that it is feasible to use parallel baseline in phase unwrapping directly.

parallel baseline; InSAR; phase unwrapping

2015-07-27。

刘志铭(1973—)，男，副研究员，主要从事雷达摄影测量研究。

P231

A