一种BDS星钟异常实时探测与处理算法

赵　丹，周佩元，杜　兰

信息工程大学导航与空天目标工程学院，河南 郑州，450001



一种BDS星钟异常实时探测与处理算法

赵丹，周佩元，杜兰

信息工程大学导航与空天目标工程学院，河南 郑州，450001

通过连续监测钟差时序数据，可以快速探测星载原子钟异常，从而确保卫星导航系统的完好性。本文结合广义似然比检验(GLRT)方法和多项式钟差模型，提出了一种新的实时原子钟异常探测与处理方法：首先，基于GLRT方法进行实时异常探测；然后采用多项式钟差模型进行短期钟差外推，在此基础上剔除异常值并以估值代替；最后，利用武汉大学分析中心提供的精密BDS钟差数据进行仿真。验证结果表明，该方法能够快速有效地探测和处理原子钟异常(尤其是频率跳变异常)，较好地保证了BDS原子钟数据的完好性。

BDS星钟；原子钟异常探测；GLRT探测器；钟差模型

1　引　言

原子钟是许多复杂系统的关键部件之一，如电信网络系统、电力系统以及全球卫星导航系统等[1]。原子钟信号优异的计量学特性是实现这些应用的基础。但是在原子频标长期运行测量过程中，常会由于断电、设备故障和外部干扰等因素引起数据异常，如信号缺失、频率漂移、相位跳变和频率跳变等[10]。因此，必须对原子钟进行实时监测和评估，对其异常进行实时探测和处理，并在短时间内给终端用户发出告警信号。

近年来，国内外学者在原子钟异常数据的分析和处理上做了许多有意义的工作，提出很多有效的原子钟异常探测算法，如最小二乘法、阿伦方差法、基于中位数(MAD)的抗差估计法、卡尔曼滤波器法以及最大似然比检验法等[2-7]。但是这些方法在实时性上都存在一些不足，其中，最小二乘法、阿伦方差法和基于中位数的抗差估计法主要用于对事后钟差数据进行处理，而卡尔曼滤波器法和最大似然比检验法的参数选取比较复杂。目前，我国对BDS星载原子钟完好性的研究相对较少，值得进一步研究。为了保证实时导航定位用户的需求，必须对原子钟进行实时的异常识别、解释和处理。

已有研究表明，原子钟的频率数据服从高斯白噪声分布，其均值和方差与时间有关[4]。因此，本文基于BDS星载原子钟的时频特性，结合广义最大似然比估计和钟差多项式模型，提出了一种便捷可靠的实时BDS原子钟异常探测与处理算法。仿真结果表明，该算法能够有效地对频率跳变异常进行探测和处理。

2　基于广义似然比检验的原子钟异常实时探测与处理算法

为了实现对原子钟异常的实时探测与处理，本文对广义似然比检验进行了改进，提出了一种快速的阈值选取方法；然后利用该方法进行原子钟异常的探测，并利用实时的钟差预报模型计算出异常点的估计值，从而实现对原子钟异常的修复。

2.1广义似然比检验(GLRT)

广义似然比检验是一种快速有效地探测均值和方差变化的方法，文献[4]的研究表明，正常工作模式下原子钟的频率数据服从高斯白噪声分布。因此，广义似然比检验能满足实时原子钟异常探测的要求。

2.1.1GLRT基本原理

基于原子钟频率数据服从高斯白噪声分布的前提，可以用两个假设H0和H1来描述其模型参数的变化。H0(零假设)表明样本数据y[n],n=0,…,N-1服从于均值为μ0、方差为σ0的高斯概率密度函数；H1(备择假设)表明样本数据的均值和方差发生了改变，均值变为μ1或者方差变为σ1。上述假设可以用下面的等式来描述：

(1)

式中，n0为未知的跳变点，需要对其进行估计。

因此，利用最大似然估计法判断H1假设成立的准则[4,5]为：

T(y)=log(LG(y))=log(p(y;[μ0,σ0,μ1,σ1,n0],H1))-log(p(y;[μ0,σ0],H0))>γ

(2)

式中，LG(y)为似然比，p(y;[μ0,σ0],H0)和p(y;[μ0,σ0,μ1,σ1,n0],H1)分别为假设H0和H1成立下序列的概率分布，γ为判断零假设成立与否的阈值。为了便于计算，T(y)取似然比的对数形式。

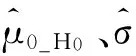
将式(2)中的未知参数用其最大似然估计值代替，则式(2)可化为：

(3)

需要指出，为了保证算法的实时性，仅对序列的最后一个值进行异常探测，同时，需要将n0值固定。因此，当取定一个γ值后，即可进行异常的判断。

2.1.2GLRT阈值γ的选取

在进行GLRT方法计算的过程中，关键之处在于γ值的选取。常用的方法为通过计算ROC曲线来选取[4,8]，这需要计算正确检测的概率(PD)以及发出错误警告的概率(PFA，即H0假设成立时选择H1假设)。这种常用的判断γ的方法虽然能够确定一个可靠而且精确的阈值，但是选取阈值时需要进行蒙特卡洛实验，计算量较大，不适合实时异常探测。因此，本文提出了一种新的快速确定γ取值的方法，其步骤如下。

(1)已知数据分段。将已知无异常频率数据Y分为三部分Y1、Y2和Y3，并假设Y3为“待探测”数据，则数据结构如图1所示。

图1　数据结构示意图

从上图可以看出，Y1和Y2均服从于同一正态分布N(μ0,σ0)。在已知序列Y2中加入待探测数据y[N]后，若y[N]为无异常数据，Y2仍服从正态分布N(μ0,σ0)，否则Y2将不再服从N(μ0,σ0)。

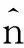
γ=max(T(y))

(4)

2.2异常处理算法

常见的原子钟模型有很多，如多项式模型、灰色系统模型、卡尔曼滤波器模型等[9]。考虑到算法的复杂性与计算量，本文采用最简单且短期预报精度高的多项式模型对已知数据进行建模。不同星载原子钟的频率漂移特性有所不同，故针对星载铯钟和铷钟的多项式模型可表示为：

(5)

式中，a、b、c为多项式模型的未知参数，ε为白噪声。

通过最小二乘拟合求解出多项式模型的参数，再利用该模型进行预报。需要指出，对原子钟异常的探测常常是基于频率数据，而对原子钟的预报采用钟差(即相位)数据，故需要通过一次差分将钟差数据转换为频率数据。

2.3算法描述

基于前文所述，本文设计了一种基于GLRT方法的实时原子钟异常探测和基于钟差多项式模型预报的异常处理算法。其主要步骤如下：

(1)数据截取。从无异常的钟差历史序列中截取序列X及其相对应的频率序列。

(2)确定阈值。利用频率序列Y计算得到T(y)序列，取其最大值为GLRT探测器的判断阈值。

(5)异常警告。重复上述步骤，探测下一个待探测频率数据点；当连续出现异常警告次数超过N/2时，说明原子钟发生了持久性的频率跳变，需要重新选择钟差序列X和频率序列Y。

在上述流程中，需要注意几点：(1)钟差序列X仅仅在出现异常值时作为已知数据建立钟差模型，GLRT探测时使用的是频率数据(一阶差分)；(2)在新的钟差数据输入时，只需要对其进行一次差y[i]=x[i+1]-x[i]即可。

3　算例验证与分析

在星载原子钟常见异常现象中，信号缺失是由于原子钟发生故障或彻底丧失信号输出功能，而频率漂移在多数情况下可以人工建模预测并修正。星载原子钟单纯的相位跳变很少发生，通常相位跳变是频率跳变的间接反映，因此最常见的原子钟异常为频率跳变[10]。本节基于武汉大学分析中心提供的BDS精密钟差数据，验证了原子钟频率跳变探测与处理的有效性。

3.1数据设计与仿真

频率跳变通常分为暂时性跳变和持久性跳变。在实时原子钟异常探测的情况下，持久性跳变可以看作暂时性跳变的累积。因此，本文设计了BDS原子钟两种情况的暂时性频率跳变：(1)单点频率跳变；(2)连续多点频率跳变。然后利用本文算法进行了异常探测与处理，以此验证算法的有效性。

本文使用的样本数据是武汉大学分析中心提供的2013年1月8日采样周期为5分钟的精密钟差数据，选取BDSC01号卫星作为研究对象，其钟差和频率数据如图2所示。

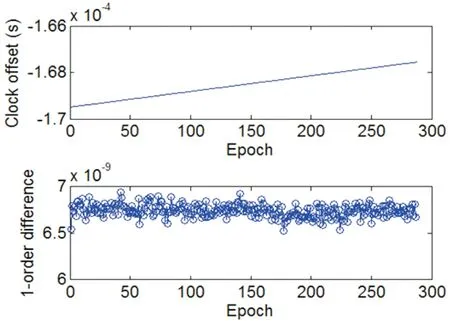
图2　BDS C01星载原子钟的钟差与一阶差分(频率)序列

从图2可以看出，其频率数据基本上满足高斯白噪声分布，证实了本文算法的前提条件，即星载原子钟的频率数据服从高斯分布。由于原子钟出现异常是小概率事件，因此，难以得到带有异常事件的钟差数据，本文采用文献[11]的方法，即在正常钟差数据的叠加异常数据表征异常。在该频率序列n=150、n=210、n=211、n=212处分别加入人为的“暂时性跳变”，该异常大小为均值的2、3、3、3倍，加入异常后的频率序列如图3所示。

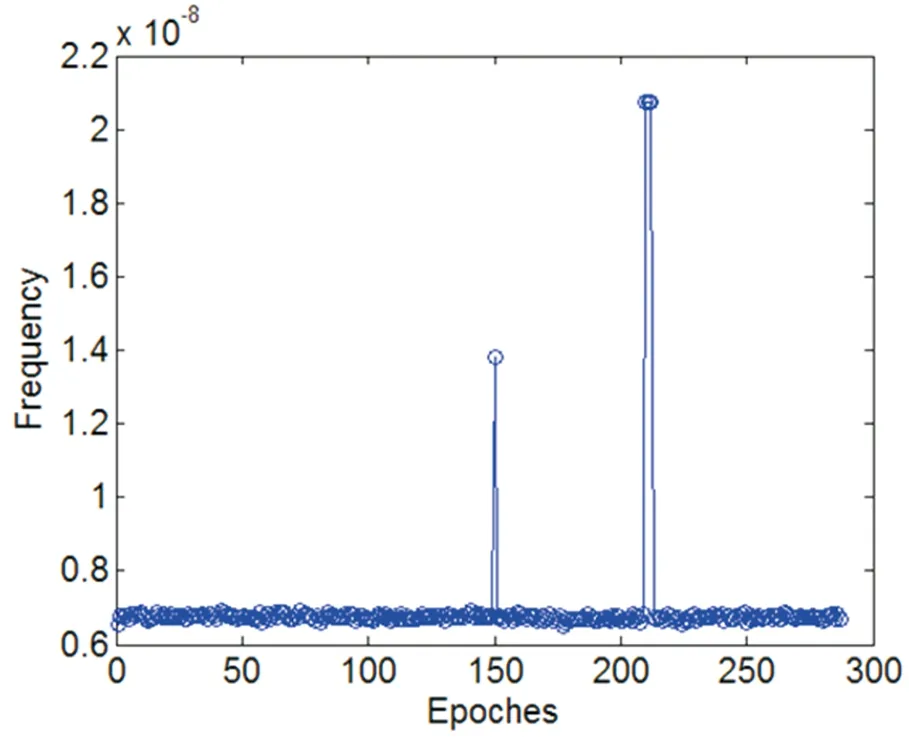
图3　在原始频率数据中加入人为异常后的频率序列

3.2算例结果

首先，从历史无异常钟差序列中截取长度为140的序列进行阈值确定。令滑动窗口长度为116，其中子窗口Y1、Y2长度分别为100和15(固定n0=100)，“待检测”序列长度为25。利用Y1和Y2对Y3进行检验计算得到T(y)，将窗口滑动25次，取T(y)中最大值作为阈值，则有γ=9.475。

其次，继续滑动窗口对未知数据逐一进行GLRT探测。首先探测到n=150的异常点，T150(y)=262.05，T150(y)>γ，因此判断该点为频率跳变点，发出警告，如图4所示。为了便于对比，图中给出了对全部待探测值进行计算的T(y)序列。

图4　第一次异常警告

为了进行比较，计算异常点附近几个点的T(y)值，如表1所示。

表1异常点及其附近点的T(y)值(γ=9.475)

点号148149150151152T(y)0.501.05262.05211.20211.54

从上表可以看出，T150(y)远远大于阈值γ，并且在异常未经处理的情况下，T150(y)之后的T(y)的值也大于阈值。由此可见，一个异常数据影响了整个序列的分布。

发现异常数据后，实时对异常进行修复处理。 利用已知正常钟差序列建立多项式模型，并外推得到该点的估计值，从而对异常点进行修复。为了验证是否对该异常进行了有效的修复，再一次进行GLRT探测。从图5可以看出，这时在y[150]处并无异常，不发出警告信号。

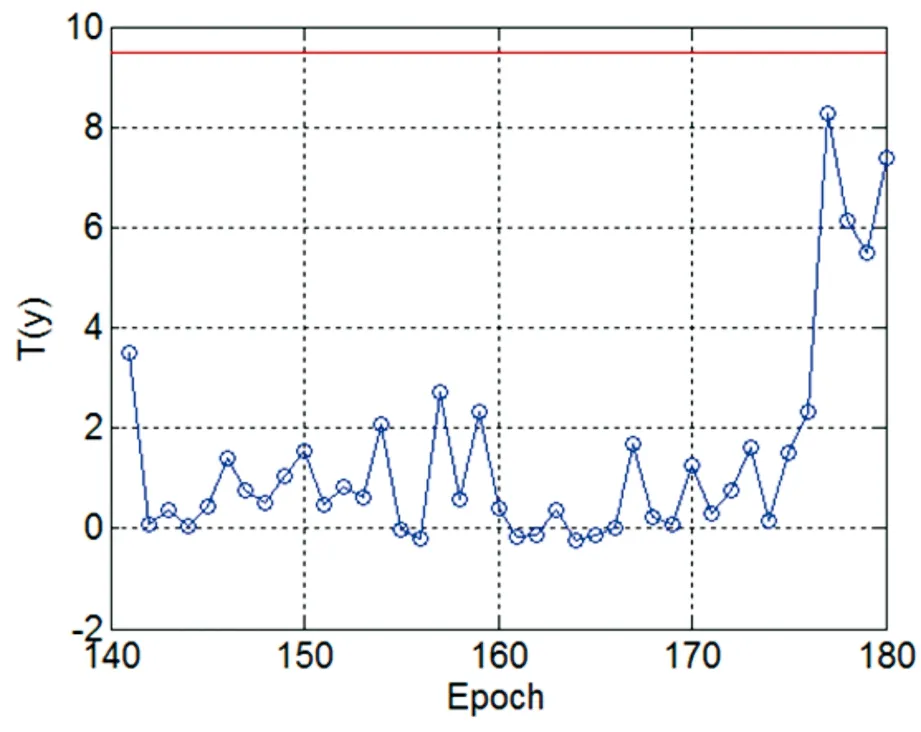
图5　修复第1个异常点后的T(y)序列

在修复完y[150]处的异常后，继续滑动窗口，进行GLRT探测。此段的T(y)值如图6所示。从图6可以看出，当检测到y[210]时，此时T(y)=343.4，T(y)>γ，因此判断该点为频率跳变点，发出警告。

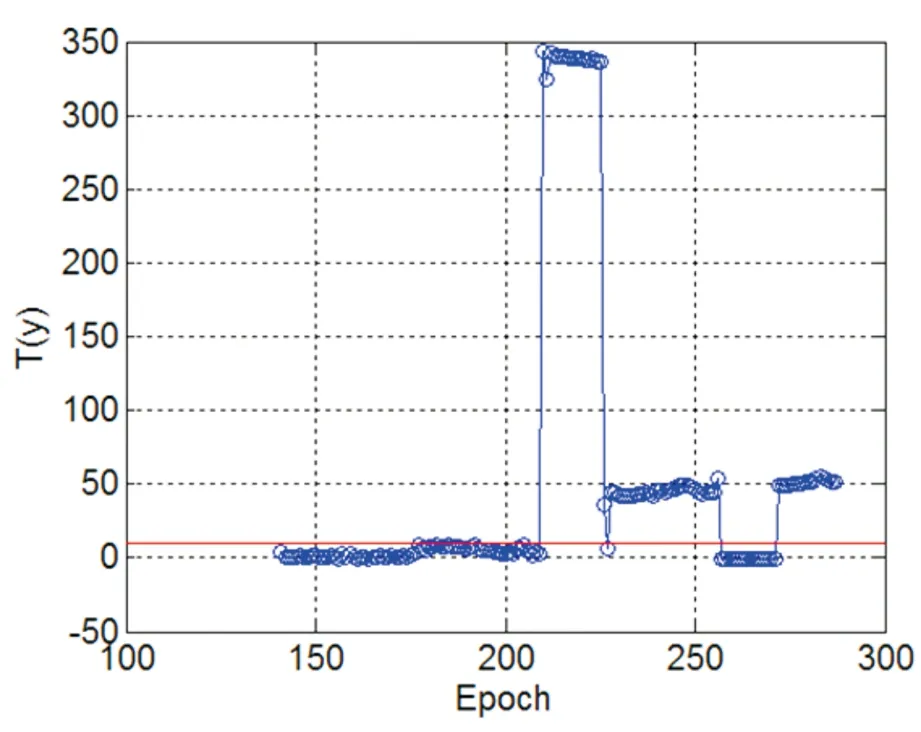
图6　第二次异常警告

对其进行修复后，再滑动窗口，可以检测出连续的三个频率跳变点。对这些异常点进行修复，平均不符值大小为3.27×10-10s。表2列出了异常处理前后的T(y)值。从表中可以看出，GLRT探测出了连续的三个频率跳变点，并通过多项式模型对这三个异常点进行了及时和有效地修复，并将误差控制在10-10s量级。

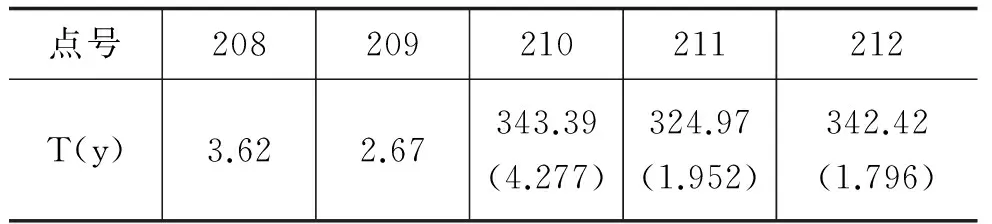
表2　异常点及其附近点的T(y)值

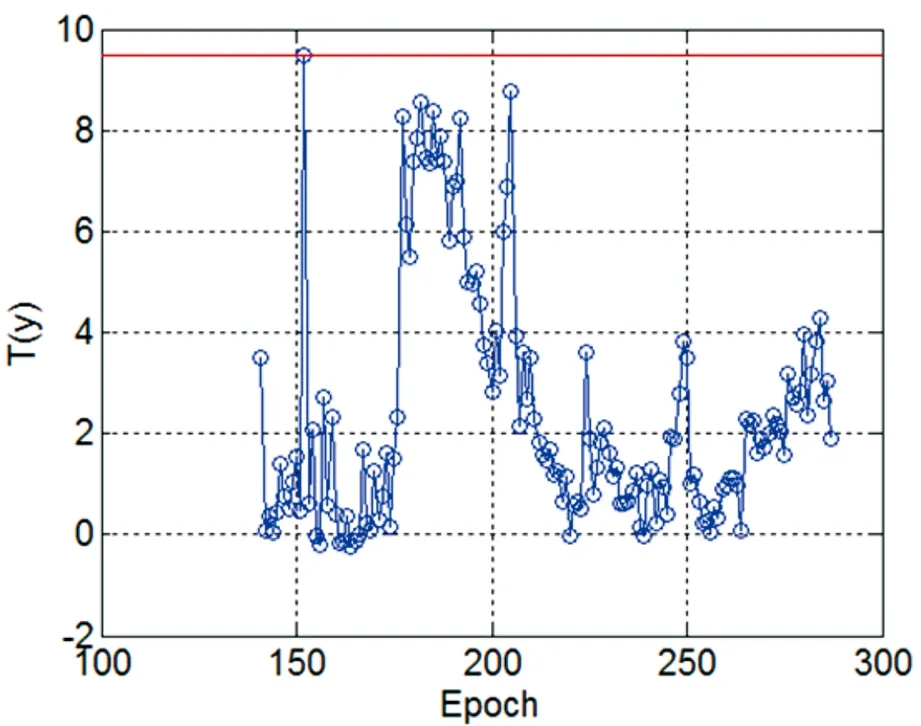
图7　修复所有异常点后的T(y)序列

4　结　论

本文给出了一种基于GLRT探测和钟差预报修复的实时原子钟异常探测和处理算法，通过两种频率跳变(单点跳跃和连续多点跳跃)的计算可以看出，该算法不仅能够有效地探测常见的频率跳变(暂时性和持久性频率跳变)，而且能及时对异常点进行警告和修复处理。该算法简单有效，自动化程度较高，对实际工程应用有一定参考意义。需要指出的是，本文算法的前提条件为存在一段已知的无异常数据，因此在不满足这一前提的条件下，如何启动该数据处理流程是下一步的研究重点。此外，本文算法中的参数可能需要根据不同数据的特性做出相应的调整，以更好地对异常进行探测和修复。

[1]MORIKAWA T. Spaceborne Atomic Clock [J]. IEIC Technical Report (Institute of Electronics, Information and Communication Engineers), 2001, 101(157): 75-81.

[2]郭海荣. 导航卫星原子钟时频特性分析理论与方法研究[D]. 郑州：信息工程大学，2006.

[3]黄新明，龚航，朱祥维.基于Kalman滤波器的卫星钟实时异常监测算法[J]. 宇航计测技术，2011，31(5): 6-11.

[4]Nunzi E, Galleani L, Tavella P, et al. Detection of anomalies in the behavior of atomic clocks[J]. Instrumentation and Measurement, 2007, 56(2): 523-528.

[5]Nunzi E, Carbone P. Monitoring signal integrity of atomic clocks by means of the GLRT [J]. Metrologia, 2008, 45(6): 103.

[6]Galleani L, Tavella P. Tracking nonstationarities in clock noises using the dynamic Allan variance[C].Frequency Control Symposium and Exposition, 2005.

[7]Weiss M, Shome P, Beard R. On-board GPS clock monitoring for signal integrity[C]. Proceedings of the 42nd Annual Precise Time and Time Interval (PTTI) Applications and Planning Meeting, 2010.

[8]Nunzi E, D'Ippolito D. A novel theoretical analysis of fault detection for atomic clock[C].Advanced Methods for Uncertainty Estimation in Measurement,2009.

[9]崔先强，焦文海.灰色系统模型在卫星钟差预报中的应用[J]. 武汉大学学报·信息科学版, 2005, 30(5): 447-450.

[10]唐升，刘娅，李孝辉.星载原子钟自主完好性监测方法研究[J].宇航学报，2013, 34(1): 39-45.

[11]牛飞. GNSS完好性增强理论与方法研究[D]. 郑州: 信息工程大学, 2008.

A Real-time BDS Satellite Clock Anomaly Detection and Processing Algorithm

Zhao Dan，Zhou Peiyuan，Du Lan

Institute of Navigation and Aerospace Engineering, Information Engineering University, Zhengzhou 450001, China

Spaceborne atomic clock anomaly can be detected quickly by continuously monitoring of clock bias, thus it ensures the integrity of satellite navigation system. This paper puts forward a new method of real-time atomic clock anomaly detection and processing combined with principles of Generalized Likelihood Ratio Test (GLRT) and polynomial clock model. Firstly, the real time anomaly detection is done based on the GLRT. Then the short-term clock bias is forecasted and extrapolated by using the polynomial clock model, and on this base, the anomaly points are eliminated and replaced by extrapolation values. This paper simulates the examples based on BDS satellite clock bias provided by Wuhan University Analysis Center. The results show that the method can detect and handle atomic clock anomalies effectively (especially abnormal frequency jumps), and it can guarantee the integrity of BDS atomic clock data.

BDS satellite clock; atomic clock anomaly detection; GLRT detector; clock bias model

2015-07-02。

国家自然科学基金资助项目(41174025)。

赵丹(1986—)，女，硕士研究生，主要从事导航数据处理算法研究。

P236

A