基于PSO聚类和ELM神经网络机床主轴热误差建模*

王续林，顾群英，杨昌祥，杨建国

（上海交通大学机械与动力工程学院，上海 200240）

基于PSO聚类和ELM神经网络机床主轴热误差建模*

王续林，顾群英，杨昌祥，杨建国

（上海交通大学机械与动力工程学院，上海 200240）

为使得数控机床热误差实时补偿更有效，提出一种基于粒子群算法（Particle Swarm Optimization，PSO）的温度测点优选方法和基于极限学习机（extreme learningmachine，ELM）神经网络的机床热误差补偿模型。利用PSO优化K均值聚类方法，实现了机床上温度测点的优化筛选。利用ELM人工神经网络建立机床热误差补偿模型，通过合理选取隐层神经元数，从而实现更精确、更有效地对数控机床热误差进行实时补偿控制。通过与传统BP（Back Propagation）、RBF（Radial Basis Function）神经网络进行对比分析，该补偿模型具有计算简便、预测精度高、结构简单等优点，可有效应用于数控机床热误差实时补偿模型。

数控机床；PSO聚类分析；ELM神经网络；热误差建模

0 引言

机床工作时，在内外热源的作用下，主轴系统各个部分都会产生不同程度的温升后，主轴和机床其他部件的空间相对位置和尺寸都将与温升前不同，产生很大差异的温度分布，进而产生不同程度的热变形，主轴热变形引起的加工误差由此产生。大量研究表明：精密加工中机床热误差是机床最大的误差源，占机床总误差的40%～70%［1］。所以，必须采取有效的措施减小热误差。误差补偿是最常用的方法之一，其技术关键是尽可能准确地进行热误差建模，即建立机床热误差和温度之间的关系。

神经网络可以任意精度逼近非线性连续函数，使之在热误差建模领域应用十分广泛［2-4］。然而传统的网络学习方法（如BP算法）又有训练速度慢、容易陷入局部极值、耗时长等诸多缺陷。因此，探索一种训练速度快并且有良好泛化性能的训练算法，是近年来的研究热点及难点。本文提出一种单隐层神经网络建模方法-基于PSO温度测点优化及ELM神经网络建模方法，可以随机给定输入层与隐含层间的连接权值及隐含层神经元的阀值并在训练过程中无需调整，只需要设置隐含层神经元的个数，便可以获得最优解，结构简单而又高效。

1 利用PSO粒子群聚类优化K-means方法进行温度测点聚类

1.1 PSO粒子群聚类方法概述

经典聚类分析算法-K均值算法由MacQuee［5］提出，具体原理是：随机从数据集中选取K个点作为初始聚类中心，然后计算比较各个样本到聚类中心的距离，把样本归类到离它最近的那个聚类中心。再在新类中取数据平均值得到新的聚类中心，不断重复此过程，如果相邻两次的聚类中心没有任何变化，则准则函数收敛，样本聚类结束。这种搜索算法简单、快速，但是存在两个固有缺点：①随机的初始值可能导致不同聚类结果，甚至无解；②该算法基于目标函数采用梯度法求解，容易陷入局部极值。这两大缺陷大大限制了其应用范围。

粒子群算法（PSO）则是一种有效的全局寻优算法，通过群体中粒子间的合作与竞争产生的群体智能指导优化搜索。PSO模型操作简单，特有的记忆使其可以动态跟踪当前的搜索情况并及时调整其搜索策略。将其与传统的K-means聚类算法相结合，不仅有效克服了传统的K均值算法存在的问题，而且有较快的收敛速度［6］。

1.2 测温点布置及数据采集

如图1所示，本试验在一台数控车床上进行温度和热误差数据的采集，在车床有关位置布置了数字式温度传感器，分别用于测量车床主轴箱T0-1、丝杠系统T2-5、机床冷却液箱T6-7和机床床身T9-15的实时温度。由于环境温度也会对机床的加工误差造成一定影响，所以需要实时测量并记录机床所处的环境温度T8。同时，固定在机床的位移传感器（图2）分别用于测量主轴X向和Z向的热漂移误差。

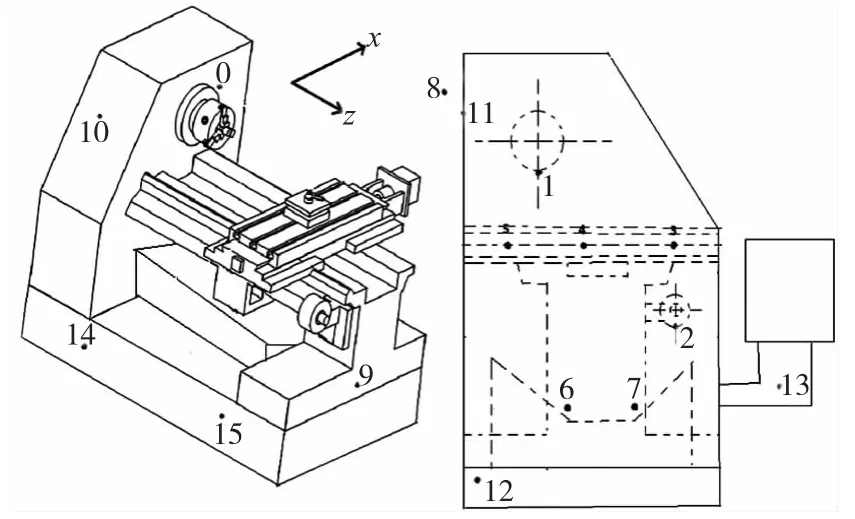
图1 温度传感器的布置

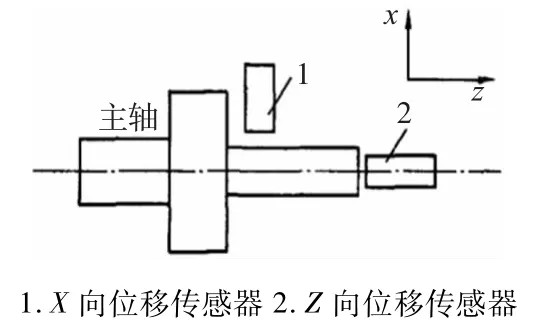
图2 非接触式位移传感器布置

在主轴2000转空载情况下，每100s采集一组数据，共240min，得机床主轴X、Z方向上温升及测量所得的热漂移误差共144组。这里仅以Z向热误差数据建模。如图3所示，随着机床的温度身高，Z向热漂移误差逐渐变大。在此期间，各温度传感器传回数据如图4。

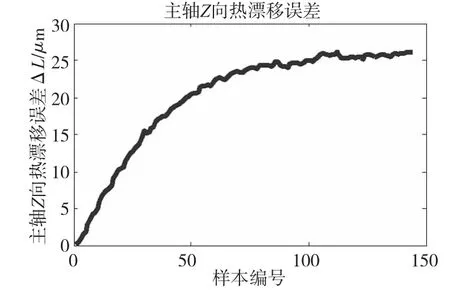
图3 主轴Z向热误差

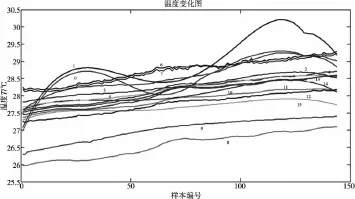
图4 温度采集数据图

1.3 温度数据编码及聚类过程

设样本集T=｛Ti，i=1，2，...，16｝，其中，Ti代表第i个温度传感器采集的所有时刻温度数据。聚类问题就是要找到一个划分集C=｛C1，C2，…，Cm｝。满足：

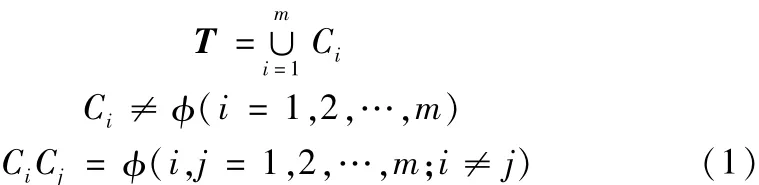
使得总的类间离散距离达到最小。

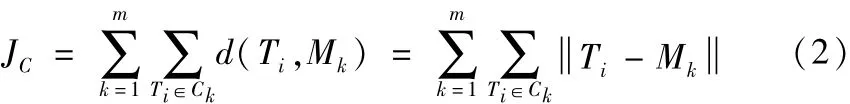
其中，Mk为第K个聚类中心（温度平均值），d（Ti，Mk）为样本到对应聚类中心的距离（欧氏空间距离），聚类准则函数JC即各类样本到对应聚类中心距离的总和。

这里基于聚类中心编码，一个编码对应于一个聚类中心可行解，每个粒子的位置由m个聚类中心组成。除了位置以外，还有粒子速度值，用于更新粒子当前的位置。由于样本向量维数为144，因此粒子的位置是m×144维变量，同时粒子的速度也应当是m× 144维变量，此外，每个粒子还有一个适应度值，适应度函数f（）T=a/JC，a是常数。故可以按以下形式作为个体粒子：

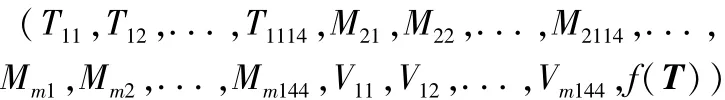
这里按照常规，设置学习因子c1、c2分别为2，惯性权重为0.4～0.9线性递减更新，具体确定聚类中心的有关公式及求解流程图如图5所示［3］。

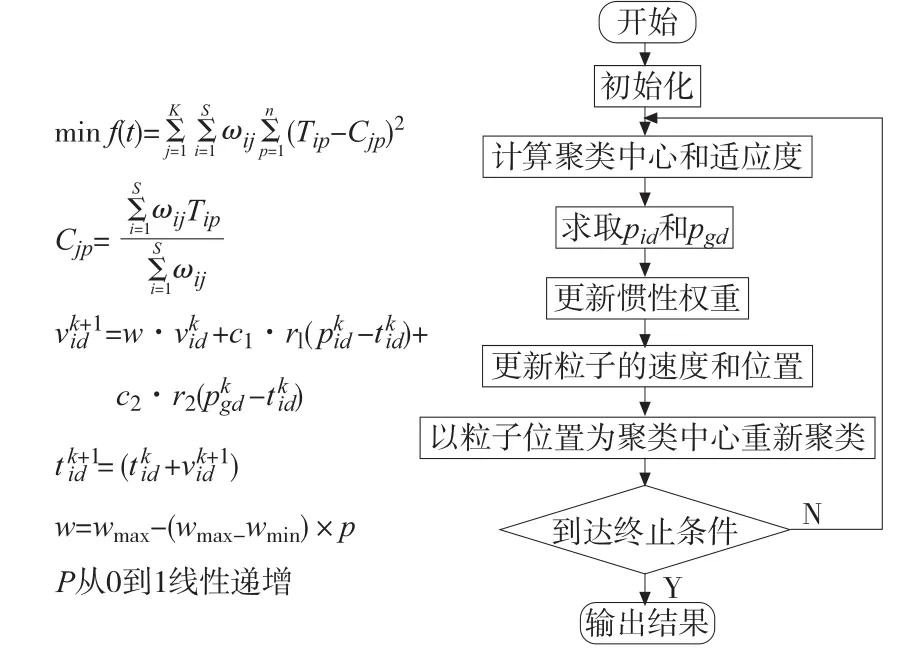
图5 PSO聚类算法流程及主要公式

当聚类中心确定时，聚类的划分由下面的最近邻法则决定。即：若Ti，Mj满足，

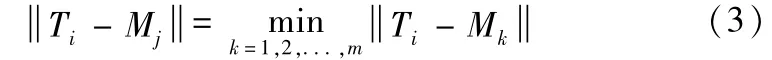
则Ti属于第j类［7］。

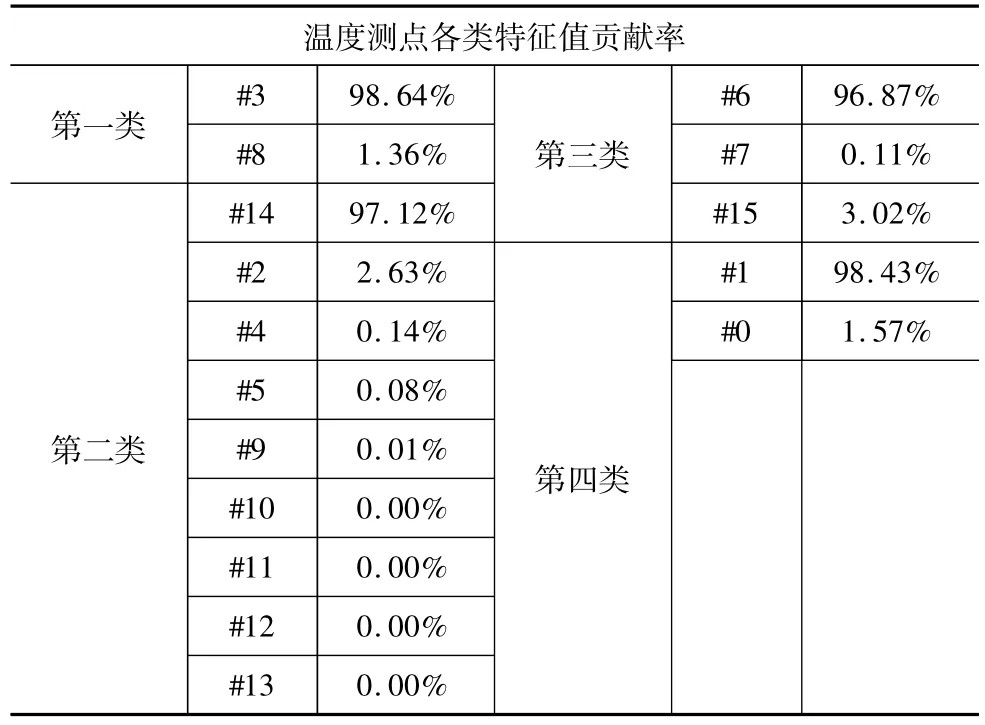
表1 温度测点信息图

总聚类数m从2开始递增取值，发现m取2、3，聚类结果难以收敛；取大于3的值，最终结果都收敛到4类。故取m为4，经过2000次迭代更新，得到的聚类结果如下四类：第一类（#3，#8），第二类（#2，#4，#5，#9，#10，#11，#12，#13，#14），第三类（#6，#7，#15），第四类（#0，#1）。这里为了得到每一类中最能表达温度信息的测点，可以利用主成分分析，对每一类特征值贡献率分析，如表1。按照最大特征值信息，最终选择Z轴丝杠螺母温度T3，主轴箱温度T1，冷却液温度T6，床身温度T14四个关键点温度用于建立热误差模型建模。

2 ELM神经网络建模

ELM神经网络结构如图6所示，该网络由输入层、隐层和输出层组成，相邻两层神经元全连接。

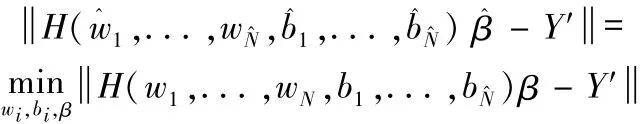
即求最小值函数

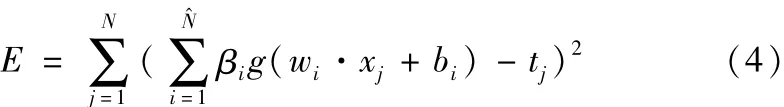
确定这些参数，就等价于求得线性方程Hβ=T′的最小二乘解。在前人研究的基础上，Huang等人提出了以下结论［8-11］：给定任意Q个不同样本（xi，ti），给定任意小误差ε（ε＞0）和一个任意区间无限可微的激活函数g：R→R，则总存在一个含有K（K≤Q）个隐层神经元的ELM，在任意赋值wi∈Rn，bi∈R的情况下，有。

因此，ELM法只要激活函数无穷可微，输入权值和隐层偏置值就能随机设置并不必调整，一旦训练开始，那么隐层输出矩阵H保持不变。如果隐层节点数等于训练样本数N，矩阵H是方矩阵而且可逆的，当输入权值wi和隐层偏置bi是随机选择的，ELM可以接近零误差逼近训练样本。但是通常情况下隐层节点数远远少于不同训练样本的数量，即。此时H不是一个方形矩阵，故此时只能求得系统的最小范数最小二乘方解：

图6 典型ELM神经网络结构

其中，H+为隐层输出矩阵H的Moore-Penrose广义逆矩阵。

如上所述，ELM模型采用单隐含层结构，并给定输入层与隐含层间的连接权值w和隐含层神经元的偏置b情况下，网络训练就是一个多元线性方程的求解，与传统神经网络相比［1-3］，结构更简单，训练更容易。建模过程主要有以下几个步骤：

（1）数据前处理，划分训练集及测试集，同一时刻下所有温度作为输入，热误差做输出，先确定隐层神经元个数，再随机设定输入层与隐含层间的连接权值w和隐含层神经元的偏置b。

（2）选择一个无限可微函数作为隐含层神经元激活函数，这里考虑非线性，选择激活函数“hard-lim”，计算隐层输出矩阵H。

（3）按公式（5）计算输出层权值。反向输入网络，至此网络训练完成。输入要预测的温度数值，计算预测输出热误差，与实际值比较。

3 模型验证及比较

同一时刻下可以把所有温度作为输入，热误差值作为输出，前100组数据用于训练，后面44组用于预测。并且分别对16点全温度和4点选择温度分别进行模拟，比较聚类及建模效果。

3.1 数据归一化及评价标准

为了减少变量差异较大对模型性能的影响，在建立模型之前先对数据进行归一化，如公式6。归一化处理后的数据在［-1，1］之间。在进行机床热误差预测时，需要对数据进行还原处理。

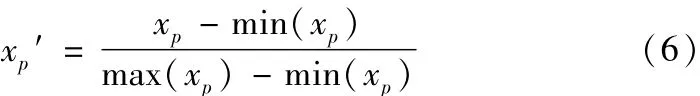
为了比较模型的预测效果，本文选定两个评价指标为最大残差Ei和决定系数R2，其公式分别如下：

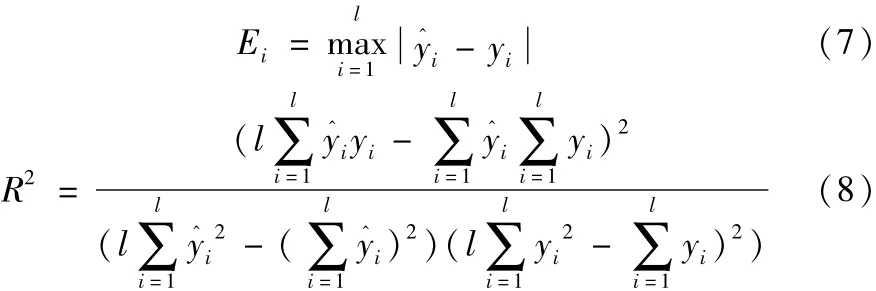
最大残差越小，表明模型的性能越好。决定系数范围在［0，1］之间，越接近1，表明模型的性能越好。反之，越接近于0，表明模型的性能越差。

3.2 隐层神经元数量选择

为了验证ELM法的可行及高效性，采用三种方法建模，分别是BP神经网络、RBF神经网络以及ELM极限学习机神经网络，均采用单隐层神经网络。由于都是单隐层神经网络，在输入层及输出层均完全相同的情况下，各神经网络的隐含层神经元数量就对建模精度影响很大。为了更好的对比建模效果，这里都采取最优数量，以保证每种神经网络单层建模效果都是最好的。

BP神经网络将网络的输出与期望输出间的误差，归结为权值与阀值的“过错”，反向传播误差“分摊”给各个神经元的权值和阀值，要求权值和阀值的调整沿着误差函数下降最快的方向-负梯度。这里隐含层神经元数目对拟合结果有很大影响［9］，如图7可见，随着神经元数目增加，预测误差逐渐增大，越来越不稳定，所以为了效果最好，本次BP网络训练选择隐层神经元数目为4，保证BP网络具有较好的拟合效果同时也有不错的训练速度［10］。

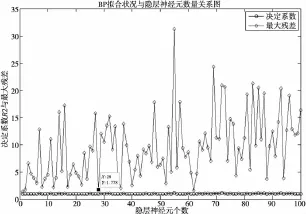
图7 BP网络拟合效果与神经元关系

RBF神经网络的基本思想是：用径向基函数作为隐含层神经元的基构成隐层空间，使得输入矢量直接映射到隐含层空间，而不需要通过权连接［11］。网络输出则是隐含层神经元输出的线性加权和。RBF神经网络的学习算法总体上可以分为两类：

（1）隐含层神经元数目逐渐增加，通过不断的迭代循环，实现权值和阀值的调整与修正。

（2）隐含层神经元数目确定（与训练集样本数目相同），权值和阀值由线性方程组直接解出。

第二种学习算法速度显然更快、精度更高，故采用。由于Matlab工具箱中RBF神经网络拟合效果还与径向基函数的扩展速度（参数spread）有关。由图8可见，Spread选取会造成拟合的失效，这里取spread为0.001，满足效果情况有较好的训练速度同时有较好的精度。

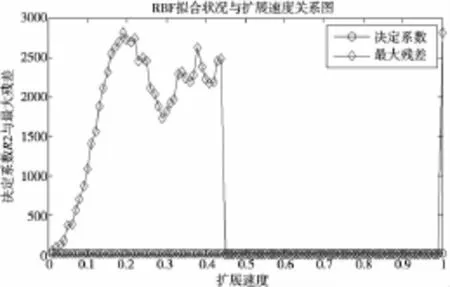
图8 RBF网络预测效果与扩展速度关系

如前所述，当隐含层神经元与训练集样本个数相等时，ELM网络可以迅速零误差逼近所有训练样本。但是，并非隐含层神经元个数越多越好。由图9可知，ELM网络建模精度随隐层神经元个数都很好，在保证正确率的情况，选择隐层神经元数目为85。

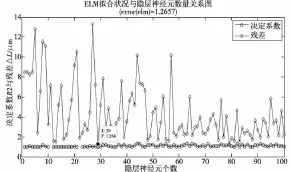
图9 ELM法与隐层神经元数目关系

3.3 网络训练及预测结果分析

为了检测PSO温度测点选择效果，把4点温度关键点和原始16组数据分别建模并进行对照，由三种神经网络经过训练、预测，其拟合结果如图10、图11，性能参数如表2。

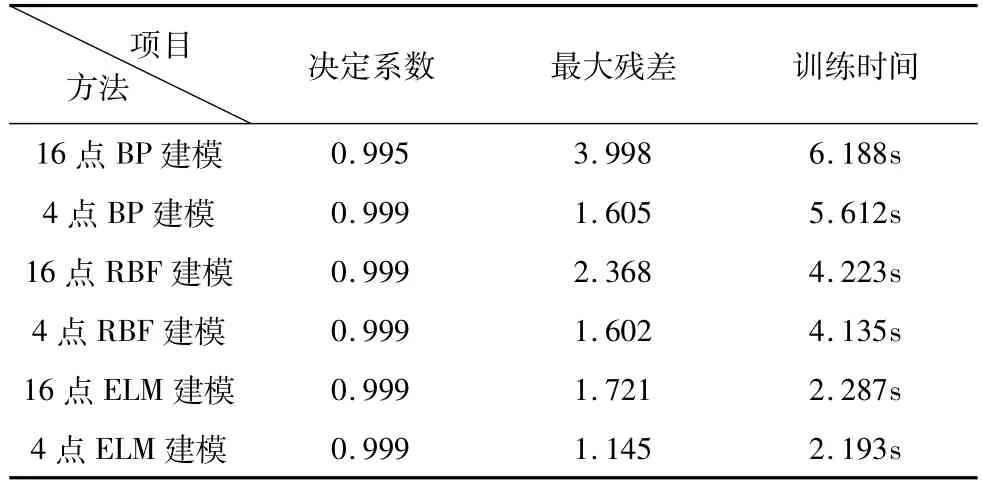
表2 三种方法预测效果分析表（μm）

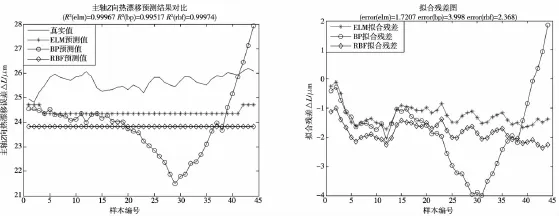
图10 16温度测点热误差预测结果

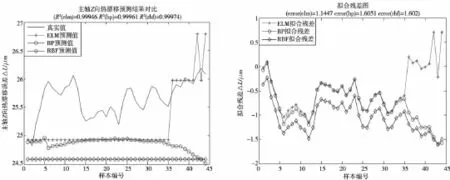
图11 4温度测点热误差预测结果

从表2、图10、图11不难看出：①利用PSO方法进行温度测点选择，在温度数据从16组缩减至4组而其他条件相同情况下，各方法建模精度及运算速度反而均有了较大提升，说明采取PSO优化温度测点方法是有效的。之所以全温度数据建模预测精度反而劣于四点关键温度数据建模，是因为某些温度数据是由其他温度藕合而成并非有效温度，造成建模预测精度降低。②不管是否采取温度测点优化，ELM模型都能有效跟踪机床热误差的变化，其最大残差在2μm以内，且波动幅度要小于BP、RBF网络，而运行速度明显快于BP、RBF网络，建模性能优于传统神经网络。③ELM网络预测结果与RBF网络大致呈现近似走势，其实分析两者结构可知ELM与RBF不同之处在于随机产生输入层与隐含层连接权值和隐含层神经网络偏置（其激活函数均为径向基函数）。所以，本质上RBF网络是ELM网络的一个特例。

4 结论

（1）基于PSO温度测点优化方法可以用于选取关键温度数据，可以显著加快数据建模速度。

（2）ELM神经网络相对于其他模型来说，具有建模精度高、训练快，结构简单且调节参数少等优点，适合作为各种复杂加工场合中的机床热误差补偿模型。

（3）PSO粒子群理论和ELM神经网络结合在一起，可以有效地避免了单一数学模型丢失信息的缺点，大幅提高了热误差补偿模型的预测精度。

［1］张毅，杨建国.基于灰色神经网络的机床热误差建［J］.上海交通大学学报，2011，45（11）：1581-1586.

［2］陈莉，贾育秦，毕有明，等.基于神经网络数控机床热误差建模的研究［J］.机电工程技术，2011，40（1）：16-57.

［3］苏铁明，叶三排，孙伟.基于FCM聚类和RBF神经网络的机床热误差补偿建模［J］.组合机床与自动化加工技术，2011（10）：1-4，9.

［4］沈岳熙，杨建国.基于岭回归的数控机床温度布点优化及其热误差建模［J］.机床与液压，2012，40（5）：1-3.

［5］MacQueen J.Some methods for classification and analysis of multivariate observations［C］.In：proceedings of the 5th Berkeley Symposium on mathematics Statistic Problem，1967，l：281-290.

［6］周弛，高海兵，高亮，等.粒子群优化算法［J］.计算机应用研究，2003（12）：7-11.

［7］刘靖明，韩丽川，候立文.一种新的聚类算法粒子群聚类算法［J］.计算机工程与应用，2005（20）：183-185.

［8］G B Huang，Q Y Zhu，C K Siew.Extreme learning machine：Theory and applications［J］.Neurocomputing，2006，70（l-3）：489-501.

［9］G B Huang，Q Y Zhu，K Z Mao，et al.Can threshold networks be trained directly［J］.IEEE Transactions on Circuits and Systems II：Express Briefs，2006，53（3）：187-191.

［10］G B Huang，H A Babri.Upper bounds on the number of hidden neurons in feedforward networkswith arbitrary bounded nonlinear activation functions.IEEE Transaction on Neural Networks，1998，9（1）：224-229.

［11］G.B.Huang.Learning capability and storage capacity of two hidden-layer feedforward networks.IEEE Transaction on Neural Networks，2003，14（2）：274-281.

（编辑 李秀敏）

M odeling for M achine Tool Thermal Error Based on PSO Clustering Algorithm and ELM M odel Preprocessing Neural Network

WANG Xu-lin，GU Qun-ying，YANG Chang-xiang，YANG Jian-guo
（School of Mechanical Engineering，Shanghai Jiaotong University，Shanghai200240，China）

In order to improve the precision of real time compensation for thermal error on NCmachine tool，this paper proposed a method which is based on the PSO temperature measuring point clustering and the modeling of ELM neuralnetwork for thermalerror compensation in NCmachine tools.K-means clustering is optimized by PSO algorithm so as to decrease the number of the temperature sensors.And then the ELM neural network is established the thermal errormodel based on themain temperature points so thata NCmachine tool is online compensatedmore effectively.Compared with BP，RBFmethods，ELM neuralnetwork has an advantage of calculation speed，structure and precision which could be used to the real compensation for NCmachine tools.

NC machine tool；PSO-Kmeans clustering；ELM neural network；thermal errormodeling

TH165；TG659

A

1001-2265（2015）07-0069-05 DOI：10.13462/j.cnki.mmtamt.2015.07.019

2014-09-12；

2014-11-27

国家自然科学基金项目（51275305）；2013年度上海市引进技术的吸收与创新技术项目（13XI-07）；辽宁省科技创新重大专项（201301001）；国家科技重大专项课题（2011ZX04015-31）

王续林（1989-），男，江苏扬州人，上海交通大学硕士研究生，研究方向为误差补偿，（E-mail）sjoker@mail.sjtu.edu.cn；通讯作者：杨建国（1956-），男，上海人，上海交通大学教授，博士生导师，工学博士，研究方向为精密加工与测试、数控机床误差检测、建模和实时补偿技术，（E-mail）jgyang@sjtu.edu.cn。