可变磁路式永磁悬浮系统模型辨识与分析*

孙 凤，李 清，金俊杰，段振云

（沈阳工业大学机械工程学院，沈阳 110870）

可变磁路式永磁悬浮系统模型辨识与分析*

孙 凤，李 清，金俊杰，段振云

（沈阳工业大学机械工程学院，沈阳 110870）

可变磁路式永磁悬浮系统结构复杂，很难得到较准确的数学模型，而系统辨识方法是解决问题的有效途径。文章阐述了永磁悬浮系统结构及其工作原理，并根据其运行机理及相关准则通过数学方法建立系统平衡位置处电流-磁铁转角-位移之间关系模型；其次，通过悬浮实验采集真实输入输出数据，利用模型辨识方法获得系统ARX模型，对比两种系统模型受阶跃扰动的仿真结果表明：辨识模型的最终稳态值与实际结果一致且调节时间短，振荡次数和实际结果吻合，系统响应特性较好；理论模型的阶跃响应存在稳态误差且振荡次数多，调节时间长，这是由于理论模型中结构参数测算误差导致的仿真结果偏差。

永磁悬浮；模型辨识；阶跃响应；稳态误差

0 引言

磁悬浮技术具有无接触、无摩擦、高精度、无需润滑等一系列优点，使磁悬浮技术的应用越来越广泛，目前主要应用于磁悬浮列车、磁轴承等领域［1-3］。磁悬浮技术主要分为电磁悬浮技术及永磁悬浮技术，电磁悬浮技术的不足之处在于高耗能、应用过程中需要持续不断的供电。而永磁悬浮技术具有节能，永不失磁等优点，能有效解决磁悬浮技术高制造成本的缺陷，对于磁悬浮技术的普及与推广具有重要意义［4-5］。

永磁悬浮技术的突出优点，使其快速成为当今的科研热点并能有效解决复杂问题，新型永磁悬浮轴承应用于透平机及心脏泵中，解决了传统旋转式心脏泵摩擦所带来的溶血、血栓等问题［6-7］。永磁隔振器的设计应用可提高超精密等加工场合零部件加工精度［8-10］。永磁悬浮系统的提出及研究集中于结构设计、参数优化、磁力分析等方面，求得永磁悬浮系统的精确模型对于上述问题的研究至关重要。目前，研究者们主要根据系统结构、运行机理、物理规律等知识消除中间变量获得动力学模型，但永磁悬浮系统的强非线性特性给理论模型的建立带来了较多困难，而基于实验数据的系统辨识方法无需深入了解系统运行机理，对于复杂系统建模更具优势［11-13］。

本文提出通过改变磁通量继而改变导磁悬浮物悬浮力的可控磁路式永磁悬浮系统。系统中，磁通量由盘状永磁铁产生，通过铁轭及悬浮物构成闭合导磁回路。因此，通过电机旋转改变永磁铁转角可使回路中的磁通量改变，继而改变悬浮力的大小。

本文首先阐述了系统结构及悬浮原理并建立系统理论模型。其次，依据实验数据利用系统辨识方法获得系统ARX（extended auto-regressivemodel，扩展自回归模型）模型。最后，分别给予两种方法所得模型相同的阶跃扰动，并对结果进行分析和总结。

1 系统悬浮原理

本文提出的可控磁路式永磁悬浮系统结构如图1所示。该装置主要由径向磁化的盘状永磁铁、两个铁轭及导磁铁棒组成。两个“F”形铁轭对立安装在盘状永磁铁两侧，导磁铁棒安放在两铁轭正下方。

图1 系统工作原理图

设定图1a所示状态为初始状态，此时永磁铁转角为0°，N极在正上方，S极在正下方。由N极发出的磁力线分别经两铁轭回到S极不经过铁棒，铁棒和铁轭之间无悬浮力产生。如图1b所示，永磁铁旋转30°角，部分磁力线从N极出发经右铁轭、导磁铁棒、左铁轭构成的回路回到S极，因此铁棒与铁轭之间存在悬浮力。随着永磁铁转角的增大，流经铁棒的磁力线也不断增加，悬浮力增大，说明两铁轭与铁棒间的悬浮力可通过改变永磁铁转角大小来控制。

2 理论模型建立

系统结构参数如图2所示。图中m为铁棒的质量；fm为铁棒与铁轭之间的吸引力；d表示铁棒与铁轭间的悬浮气隙；D为导磁铁轭与永磁铁间的气隙；z表示铁棒偏离稳定悬浮处的垂直位移（向上为正）；θ为盘状永磁铁回转角（顺时针方向为正）；g为重力常数。当D，d一定时，悬浮力与永磁铁转角间的关系如图3所示：

图2 模型图示及符号定义

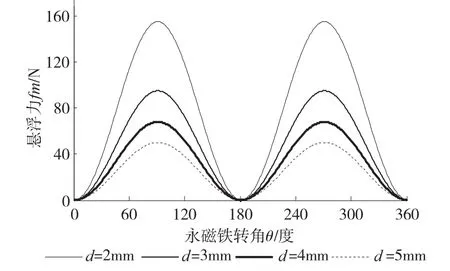
图3 悬浮力与磁铁转角关系图

由图可知铁棒悬浮力fm是关于气隙长度和永磁铁转角的函数：

此模型是根据系统内在机理及相关定理在平衡位置处对转角θ、位移z作线性化处理所得结果。各变量值如表1所示。

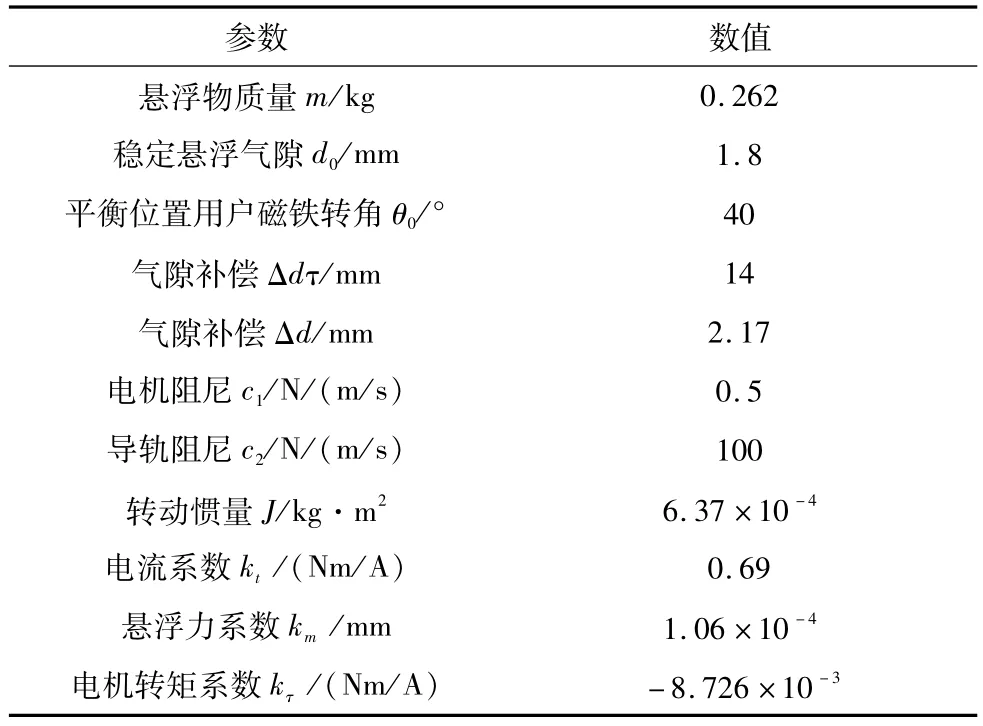
表1 系统结构参数

3 模型辨识

控制领域中，理想的控制效果与精确的数学模型是分不开的，对于复杂系统而言，系统辨识法是建立系统数学模型的有效方法。

3.1 输入输出数据采集

系统悬浮实验中用悬浮物位移与永磁铁转角双PD控制，控制器参数分别为 kp1=125930，kd1= 282.87；kp2=145.48，kd2=0.615，稳定悬浮状态如图4所示。

图4 系统稳定悬浮状态

当系统在平衡位置处稳定悬浮时，给悬浮物施加0.04mm的阶跃外扰，系统受到干扰后，通过PD2控制器的调节，永磁铁转角增大，悬浮力增加，铁棒会向上移动，通过控制系统的实时调节，永磁悬浮系统可在很短的时间内达到新的稳定悬浮状态，各参数响应情况如图5所示。

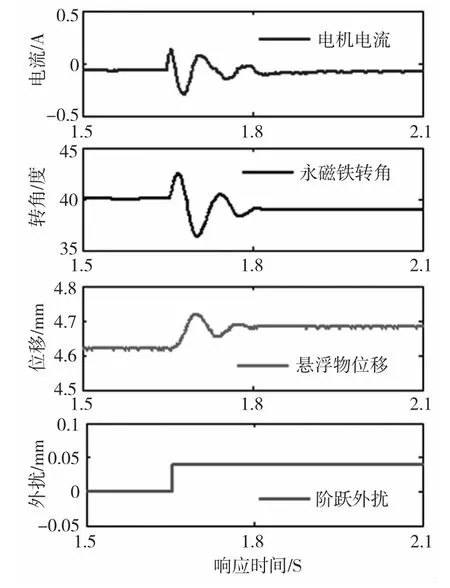
图5 系统响应曲线

3.2 模型结构选择及辨识

ARX模型（扩展自回归模型）为参数型动态系统模型，是基于实际响应来表述系统动态特性的模型。具有结构简单、鲁棒性好等优点，对于线性系统及非线性系统均有较高的辨识精度。本文选取ARX模型作为辨识模型结构，其基本结构为

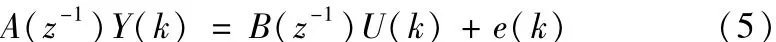
式中U（k）为系统输入，即电机控制电流；Y（k）为系统输出量，即悬浮物位移和永磁铁转角；e（k）为白噪声。z-1为后移算子；其中

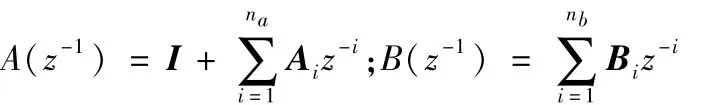
I为ny×ny维单位阵；Ai，Bi分别为ny×ny，ny× nu维矩阵。

利用系统辨识软件，选定模型阶次为na=2，nb= 5，nc=0时辨识程度高，结果如图6所示，模型结构参数为

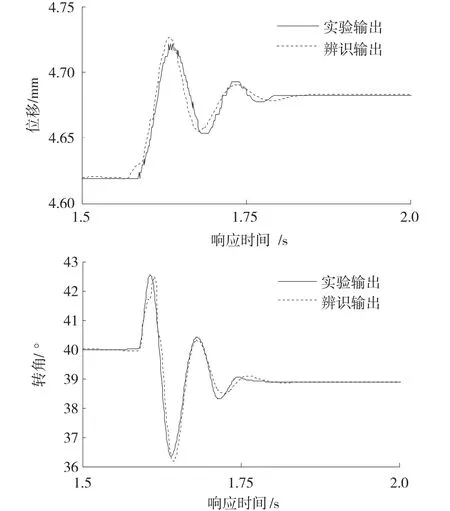
图6 模型辨识结果

3.3 模型检验

模型检验是模型辨识的重要环节，为分析模型有效性，引入均方根误差（RMSE）及相对误差（RE）来衡量其正确性，计算方法为：

图6所得辨识结果中位移输出的均方根误差为0.0055，相对误差为0.0123%；转角输出的则分别为0.1809，0.0323%。观察图6，位移及转角的辨识输出与实验输出只在方向变化时有些许差异，初始位置及新的稳定悬浮位置值均符合实际结果，图示结果及定量分析均说明模型与实际输出拟合的较好，具有较高的辨识精度，适用于系统动态分析及结果预测。

4 模型对比分析

为比较两种建模方法的差异，使用理论模型及辨识模型阶跃响应结果同实验数据比较分析。实验及仿真中均为0.03mm阶跃扰动且三种情况下均为PD控制且控制器参数相同，响应结果如图7。

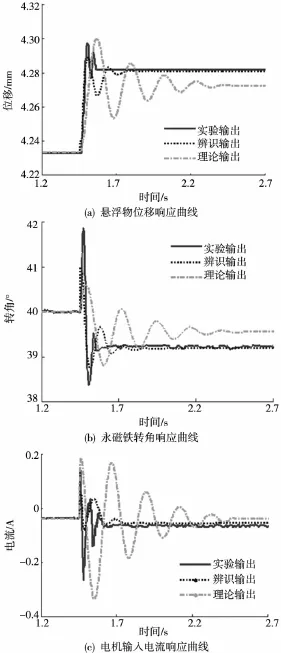
图7 阶跃响应对比

图7a为悬浮物位移响应曲线，辨识模型输出稳态值符合实验输出，动态响应过程与实验基本一致，而理论模型输出稳态误差较大，且振荡次数多；图7b为永磁铁转角响应曲线，辨识模型输出结果与实际吻合，时间响应平稳性较好，只是超调量比实际略小，而理论模型输出依然存在稳态误差且调节时间长，动态响应不能反应实验真实情况；而对于图7c电机的输入电流，辨识输出结果相比理论模型输出更符合实际情况。综合对比可见，辨识模型的输出终值与实验输出结果符合，其稳态响应较好，调节时间及系统响应过程与实验结果基本一致，动态响应特性也比较好，而理论模型的动态响应及稳态响应均不能反应系统实际运行特性；由于理论模型所涉及的结构参数是通过间接测量所得，存在不可避免的误差，且模型是在平衡位置处经过线性化得到的，这一系列的不可控因素导致了仿真结果与实际结果的偏差，而辨识模型是基于能表征系统实际运行特性的实验数据得到的，减少了测量误差对系统准确性的影响，所以辨识模型能较准确的反应系统响应特性。

5 结论

本文提出一种基于改变导磁回路有效磁通量继而改变悬浮力大小的永磁悬浮系统。并依据系统结构及磁力特性建立了理论状态空间模型；其次，利用系统悬浮实验实测数据完成模型辨识。理论模型、辨识模型及实验的阶跃响应结果对比表明：理论模型的实际输出存在稳态误差且调节时间长，儒荡次数多；而辨识模型的输出终值与实验结果基本一致，其儒荡次数少，能很快达到新的稳定悬浮状态，响应过程与实验结果基本一致，即其系统响应特性好，对于后续系统研究具有重要意义。

［1］曹永娟，黄允凯，金龙，等.磁极组合型轴向磁场无铁心永磁电机的设计与分析［J］.中国电机工程学报，2014，34（6）：903-909.

［2］胡小飞，刘刚，孙津济，等.Homopolar型径向磁轴承转子涡流损耗的分析与优化［J］.系统仿真学报，2013，25（12）：2961-2972.

［3］王军，徐龙祥.磁悬浮轴承开关功率放大器系统建模及控制研究［J］.中国机械工程，2010，21（4）：477-481.

［4］田录林，李鹏.锥形永磁轴承力解析模型［J］.中国机械工程，2014，25（3）：327-332.

［5］李云钢，程虎，张晓，等.基于V型轨道的电磁悬浮列车的悬浮导向技术［J］.同济大学学报（自然科学版），2012，40（11）：1720-1724.

［6］钱坤喜，许自豪，王颢，等.新型永磁悬浮轴承在透平机及心脏泵中的应用［J］.江苏大学学报（自然科学版），2011，32（6）：663-666.

［7］万金贵，汪希平，李文鹏，等.电磁轴承支承的透平膨胀机转子系统模态分析［J］.机械工程学报，2010，46（19）：86-91.

［8］吴国庆，钱小磊，张旭东，等.磁悬浮平台中开环磁路的漏磁通分析［J］.组合机床与自动化加工技术，2014（3）：29-32.

［9］李强，徐登峰，范新，等.新型永磁隔振器的隔振性能分析与实验研究［J］.振动与冲击，2013，32（13）：6-11.

［10］陈可，李伟，罗红波.基于Matlab的可调磁力减振镗杆控制系统参数优化［J］.组合机床与自动化加工技术，2014（3）：101-103.

［11］宋春生，张锦光，张建国.基于混合算法的磁悬浮隔振器模型辨识与验证［J］.中国机械工程，2014，25（14）：1929-1934.

［12］卜文绍，祖从林，王少杰.无轴承异步电机转子磁场定向MRAS转速辨识［J］.控制工程，2014，21（3）：334-336.

［13］张保强，郭勤涛，陈国平，等.基于复模态模型修正方法的磁悬浮轴承支承参数识别［J］.机床与液压，2008，36（4）：232-235.

（编辑 李秀敏）

M odel Identification and Analysis for Permanent M agnetic Suspension System Using Flux Path Control

SUN Feng，LIQing，JIN Jun-jie，DUAN Zhen-yun
（School of Mechancial Engineering，Shenyang University of Technology，Shenyang 110870，China）

Permanentmagnetic suspension system using flux path controlmethod have complex structures，it’s hard to get the accurate numericalmodel，the system identification method is an effective way to solve the problem.The structure and suspension principle of system is explained，the current-angle of themagnetdisplacement relation model at equilibrium position is setup based on working principles and correlation criterion.Second，acquisition inputand output data through suspension experiment，using themodel identification method to obtain system ARX model，step response of two differentmodels indicate that：the final steady state value of identification model is consistentw ith actual result and the adjusting time is short，the oscillation frequency agreew ith the reality，system response is better.The step response of theoreticalmodel have steady-state error and oscillation frequency is larger，adjustment time is long，the deviation of simulation resultsmay caused by themeasuring error of structural parameters for theoreticalmodel

permanentmagnet suspension；model identification；step response；steady-state error

TH166；TG659

A

1001-2265（2015）07-0087-04 DOI：10.13462/j.cnki.mmtamt.2015.07.024

2014-11-05

国家自然科学基金（51105257，51310105025）；辽宁省高等学校杰出青年学者成长计划（LQJ2014012）；中国博士后科学基金（2015M571327）；十二五国家科技支撑计划（2014BAF08B01）

孙凤（1978-），男，满族，辽宁阜新人，沈阳工业大学副教授，博士，研究方向为磁悬浮技术与数控技术，（E-mail）sunfeng@sut.edu.cn；通讯作者：李清（1990-），男，沈阳工业大学硕士研究生，研究方向为机电系统控制与优化，（E-mail）sutliqing@163.com。