基于ADAMS平面转弯带式输送机的动态特性

李阳星,　李晓辉

(黑龙江科技大学 机械工程学院, 哈尔滨 150022)



基于ADAMS平面转弯带式输送机的动态特性

李阳星,李晓辉

(黑龙江科技大学 机械工程学院, 哈尔滨 150022)

随着带式输送机应用范围的扩大,以及带速的提高,动态特性问题成为影响带式输送机运行的重要因素,同时,输送路线受到地形地貌以及建筑物等障碍物的影响,导致带式输送机需要曲线布置。运行参数、弯曲段布置参数等对输送机稳定运行也有很大的影响。特别是大型高速平面转弯带式输送机需要研究其动态特性。利用Pro/E建立平面转弯带式输送机结构模型,应用动态分析软件ADAMS建立虚拟样机模型,分析运行速度、输送带刚度、转弯半径和转弯角度对平面转弯带式输送机动态特性的影响。结果表明:在允许范围内,增大输送带的刚度,可以减小启动过程中输送带张力和偏移量的峰值,提高运行的稳定性,输送带的张力和转弯处偏移量随转弯角度的增大而增加,大角度转弯会降低输送带的稳定性。

带式输送机; 平面转弯式; 动态特性

0　引　言

随着带式输送机的广泛应用,单机运距不断加大,输送路线受到地形地貌以及建筑物等障碍的影响,致使带式输送机不能在输送的起点和终点之间进行直线布置。如何使其能够绕开障碍物而弯曲运行成为带式输送机发展的研究重点[1-5]。随着带速的提高,动态特性问题成为影响带式输送机运行的重要因素。近年来,对带式输送机的动态特性的研究取得了一些成果[6-12],但对在平面内可以不借助强制措施的情况下,就能实现弯曲运行的带式输送机开展动态特性研究的文献鲜见,使得弯曲运行带式输送机动力学设计难以有效开展。因此,对平面转弯带式输送机进行动态特性研究具有现实意义。

1　虚拟样机模型的建立

1.1输送带的动力学模型

由于输送带具有粘弹特性,所以在对平面转弯带式输送机的动态特性进行仿真分析时，必须把输送带作为柔性体考虑。基于有限元理论,把输送带离散成若干个小带块后，用伏格特模型连接起来。平面转弯带式输送机由于直线段和转弯曲线段的输送带的受力情况不同,所以建立的动力学模型也是不相同的。

1.1.1输送带单元在直线段的模型

对直线运行段输送带,截取任意一个单元带块进行分析,所创建的动力学模型及其受力分析如图1所示[11]。

图1　直线段单元受力分析

(1)

整理式(1),得出i单元的动张力为

(2)

1.1.2输送带单元在弯曲段的模型

图2　转弯曲线段的动力学模型

把带块单元i两边相邻的带块单元的位移以及速度全都投影到带块单元i的对应方向上,可以得到转弯曲线段输送带的动力学方程

Fwi=0。

(3)

(4)

1.2平面转弯带式输送机虚拟样机模型

模型的建立是使用ADAMS、Pro/E以及ANSYS三个软件联合完成。滚筒、托辊、拉紧装置当作刚性体考虑,输送带当作柔性体考虑,因此平面转弯带式输送机系统的构成是刚柔混合体系。创建输送带模型时,利用Pro/E建立刚性带块单元,再利用有限元软件ANSYS对刚性带块进行柔性化处理。建立的平面转弯带式输送机虚拟样机计算模型如图3所示[14]。

图3　平面转弯带式输送机的虚拟样机模型

Fig. 3Virtual prototype model of plane turning belt conveyor

计算模型参数:滚筒直径1 m,材料属性为刚体。传动滚筒表面采用胶面材质,摩擦系数0.4;改向滚筒表面采用光面金属材质,摩擦系数是0.35。托辊直径0.1 m,直线运行部分的承载段托辊间距1.5 m,直线运行部分的回程段托辊间距3 m,曲线运行段的上下分支采用同样的托辊间距1.2 m。仿真分析中对输送物料的加载是由施加在带块上且随着位置变化的力来模拟的载荷,忽略转弯段的内曲线抬高角而造成的物料下滑,因此曲线运行部分的承载段与回程段均使用简化后的直托辊。为了增大曲线段摩擦力在曲线法向的分量来平衡因曲线运行而产生的向心力,在两个托辊的间隔处的输送带上增加一个向下的压力来模拟压辊的作用。转弯段的托辊安装前倾角最大是3°,内曲线抬高角最大是5°,排列顺序是:从直线段过渡到曲线段的抬高角是1°,而后逐渐增加,到转弯段弧长的三分之一处达到5°,至弧长的三分之二后逐渐减小,到曲线段过渡到直线段处为1°。输送带的具体参数为:线密度为8.32 kg/m,带宽1 m,带厚0.01 m,带刚度k=8.5×107N/m、带阻尼c=3.5×105Ns/m。输送机总长度是80 m,转弯运行半径是500 m,转弯角度是5°。张紧装置等效为作用在改向滚筒轴上的常力,其值为60 kN。

2　动态特性分析

2.1启动方式与检测点的选择

驱动方式采用HARRSION曲线,启动过程中的速度和加速度为

式中：v0——平稳运行速度,m/s;

tT——输送机达到平稳运行速度的启动时间,s。

仿真检测点1是即将接触传动滚筒输送带上的点,在此点主要是测试张力的变化;检测点2是平面转弯处转弯曲线的中点,依此点测试转弯处输送带的横向偏移量。传动滚筒的质心设置为坐标原点,坐标系方向如图4a所示,承载段输送带即将与滚筒相遇处在y轴方向的坐标值是正值,大小等于滚筒的半径0.5 m。

图4　输送机模型中的检测点

2.2运行速度对动态特性的影响

设定输送机平稳运行时的速度为6和8 m/s进行仿真,检测点1处张力变化结果如图5所示。运行速度为v=6 m/s的情况下,在加速度达到最大值(即启动时间t=3.1 s)时,张力达到最大值67.1 kN,平稳运行张力是55 kN;平稳运行速度为v=8 m/s的情况下,在加速度达到最大值启动时间t=3.1 s时,张力达到了最大值73.8 kN,平稳运行张力是60.1 kN。不同的输送机运行速度下输送带在启动阶段的张力变化趋势相同,但是由于运行速度大的输送机在启动阶段的加速度也比较大,在启动阶段输送带张力的最大值以及波动幅度都随着输送机平稳运行速度的提高而增大。图5中可以看到,启动阶段的张力比稳定运行时的张力要大很多,但是平稳运行后的输送带张力也随着输送机运行速度的增加而变大,且变大的趋势也在随着速度的提高而加大,因此,需要分析输送机的动态特性来验证理论设计中计算得出的最大速度值,以确保输送机的安全性。

转弯处输送带转弯中点测试点2处的横向偏移量如图6所示。

图6　不同速度时转弯中点处输送带的横向位移

Fig. 6Lateral displacement at turn of conveyor belt under different speed

由图6可知,当平稳运行速度v=6 m/s时,转弯中点处的输送带横向偏移量为0.1 m;当平稳运行速度v=8 m/s时,转弯处输送带横向偏移量为0.141 m。在两个不同的输送机平稳运行速度下,输送带都是在输送机稳定运行后的横向偏移量达到稳定值,在启动周期内存在波动,随着速度的提高,波动变大。而且随着运行速度的提高在输送机平稳运行时偏移量也随之增大,降低了输送机的稳定性。

由此可知,输送带的张力及在转弯处的横向偏移量随着输送机运行速度的提高而增大,并且速度提高得越多,增大的幅度越明显,表明运行速度越大,振动越强,稳定性越低。要提高输送机的运行速度时,必须改善输送机的动态稳定性,应在保证转弯处输送带不过度偏移的同时,输送带张力的波动幅度要保持在允许的范围。

2.3输送带刚度对动态特性的影响

其他所有参数保持不变,运行速度均设置为v=6 m/s,然后分别设定输送带刚度为8.5×107和8.5×105N/m进行仿真,检测点1处张力变化如图7所示。输送带张力均在t=3.1s时达到最大值,张力最大值分别为67.1和72.5 kN。由此可知,在启动阶段输送带张力的最大值以及波动都随着输送带刚度的减小而增大。

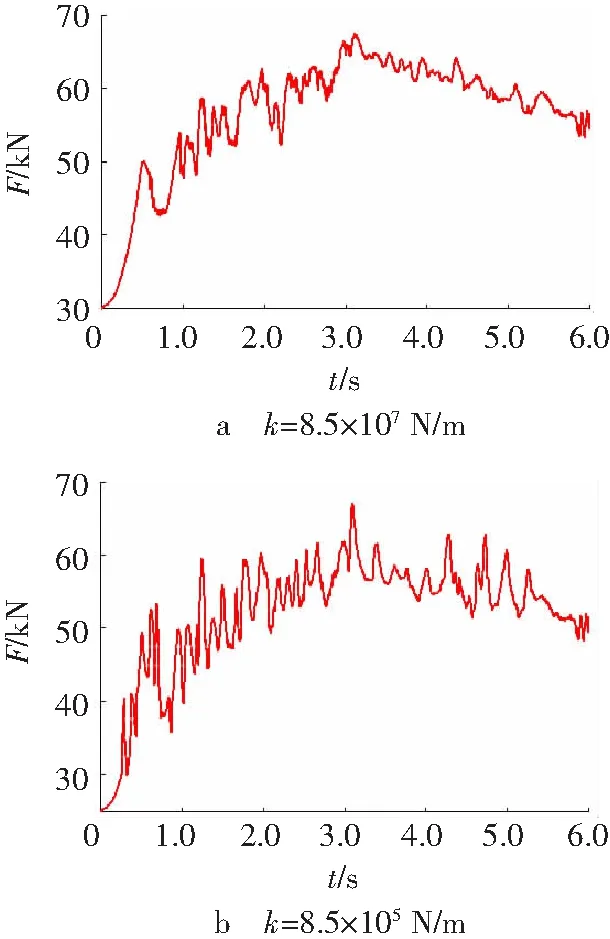
图7　输送带刚度变化时的张力曲线

转弯中点测试点2处输送带的横向偏移量如图8所示。

由图8可知,在刚度分别为k=8.5×107和k=8.5×105N/m时,偏移量在启动过程的最大值分别为0.110和0.135 m。即在两个不同的输送带刚度下,输送带在输送机稳定运行后的横向偏移量基本不变,但在启动时间段,随着输送带刚度的降低,输送机运行的稳定性下降,波动幅度加大。

图8　不同的输送带刚度下转弯处输送带的横向位移

Fig. 8Lateral displacement at turn of conveyor belt under different stiffness

综合分析曲线的数据可以得到,输送带的张力及在转弯处的横向偏移量在启动过程中的波动幅度随着输送带刚度的减小而增大,而且在启动阶段出现的张力峰值及偏移量峰值都明显增大。这是由于其他条件完全相同的情况下,输送带刚度的降低导致了输送带弹性的增加,输送带的粘弹性体现的更加明显,因而张力在输送带中的涌浪现象更加明显导致的。因此需要选择合理的输送带刚度,减小输送带的涌浪及延迟程度,减小输送机的振动,从而提高输送机的稳定性。

2.4转弯参数对动态特性的影响

2.4.1 转弯半径的影响

运行的速度均设定为v=6 m/s,其他参数保持不变,转弯角度为5°,模型转弯半径分别为550 m和450 m时进行仿真。检测点1处张力变化如图9所示。在转弯半径为550 m时启动阶段张力最大值是65 kN,平稳运行时的张力是52.5 kN;在转弯半径为450 m时启动阶段的张力最大值是71.8 kN,平稳运行时的张力是59.2 kN。在启动阶段输送带张力的最大值以及波动幅度随着转弯曲率半径的减小而增大,平稳运行后的张力值也有所增大。

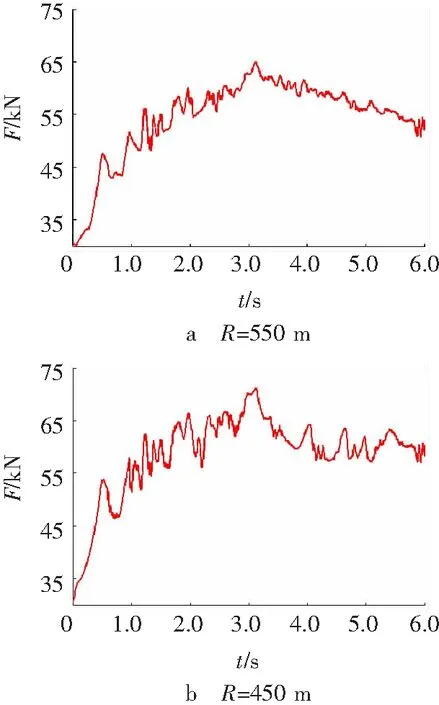
图9　转弯半径变化时输送带的张力曲线

Fig. 9Tension curve of belt conveyor when turning radius changes

转弯中点测试点2处输送带的横向偏移量如图10所示,转弯半径550和450 m时转弯中点处输送带横向偏移量分别为0.075和0.143 m,随半径减小输送带横向偏移增大,而且增大的趋势也有所增加。

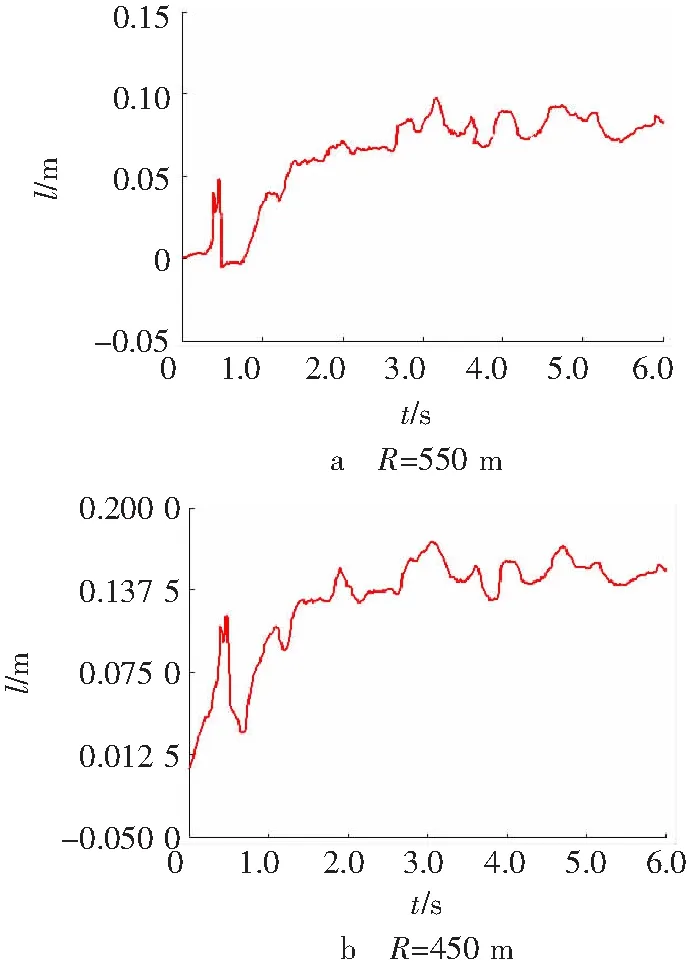
图10　不同的转弯半径下转弯中点处输送带的横向位移

Fig. 10Lateral displacement at turn of conveyor belt under different turning radius

继续减小转弯半径到400 m进行动态仿真如图11所示,由图11a可以看出,在运行到7.4 s时,张力减小到了0,而且在同一时间转弯处输送带的横向偏移量达到了0.6 m。由偏移量的曲线图可以看出,在运行到5.8 s时转弯处输送带的横向偏移量是0.2 m,而在模型创建时设置的托辊两侧比输送带宽出的长度也是0.2 m,也就是说此时曲线内侧的输送带边缘已经到了托辊支撑的极限位置。因转弯半径过小,输送带继续向内侧偏移而边缘已经离开了托辊,此时产生附加的向心力会导致更大的偏移,破坏了计算模型的正常运转,在7.4 s时驱动滚筒处的输送带已经完全与其脱离,模型完全损毁。

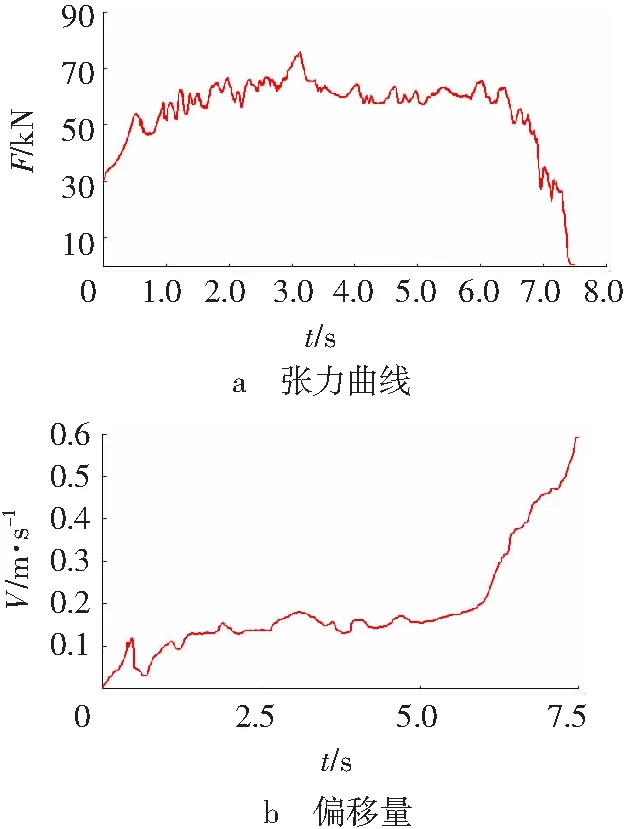
图11　转弯半径为400m时的仿真结果

综合分析曲线数据可以得到,输送带的张力随着转弯半径的减小有所增大,当弯曲半径分别为550、500、450、400 m时,最大张力分别为65、67.5、71.8、76 kN,而转弯中点处输送带的横向偏移量明显增加。弯曲运行的曲率半径一般都是按照力的平衡条件确定的,当张力无明显的变化时,转弯半径的减小导致输送带弯曲程度(曲率)增加,致使曲线两端的张力方向夹角增大,导致输送带张力矢量和增大,也就是向心力增大,致使力的平衡有所变化,使得输送带在转弯处出现了大的偏移量。弯曲半径过小如弯曲半径小于400 m时,会导致力的平衡被打破,输送带就会偏离托辊,出现不能实现自然导向转弯的情况。

2.4.2转弯角度的影响

运行的速度均设定为v=6 m/s,其他所有参数保持不变,分别建立的模型转弯角度为3°、8°进行仿真。检测点1处张力变化结果如图12所示。在转弯角度为3°时在启动阶段的最大张力值是65.8 kN,平稳运行时张力为53.5 kN;在转弯角度为8°时在启动阶段的最大张力值是68.8 kN,平稳运行时的张力为57 kN。张力值随着转弯角度的增大而增大，说明转弯角度的增大会降低输送机的稳定性。

图12　转弯半径变化时输送带的张力曲线

Fig. 12Tension curve of belt conveyor when turning angle changes

转弯测试点2处输送带的横向偏移量如图12所示,转弯角度θ=3°时偏移量最大0.105 m;转弯角度θ=8°时偏移量最大0.126 m。

综合分析曲线的数据可以得到,输送带的张力及转弯处输送带的横向位移随着转弯角度的增大而有所增大,但是波动的幅度并无特别明显的变化。跟转弯半径的影响相比,转弯角度的影响要小一些,但影响趋势有些类似,大角度的转弯会使转弯处的输送带向内侧偏移量更大,使输送机稳定性有所下降。

3　结　论

(1)相同条件下，输送机运行速度的提高导致输送带张力峰值及波动幅度增大,而且转弯处输送带横向偏移量也变大,使得输送机运行的稳定性下降。

(2)在允许的范围内，增大输送带的刚度可以减小启动过程中输送带张力和偏移量的峰值,提高输送机运行的稳定性。

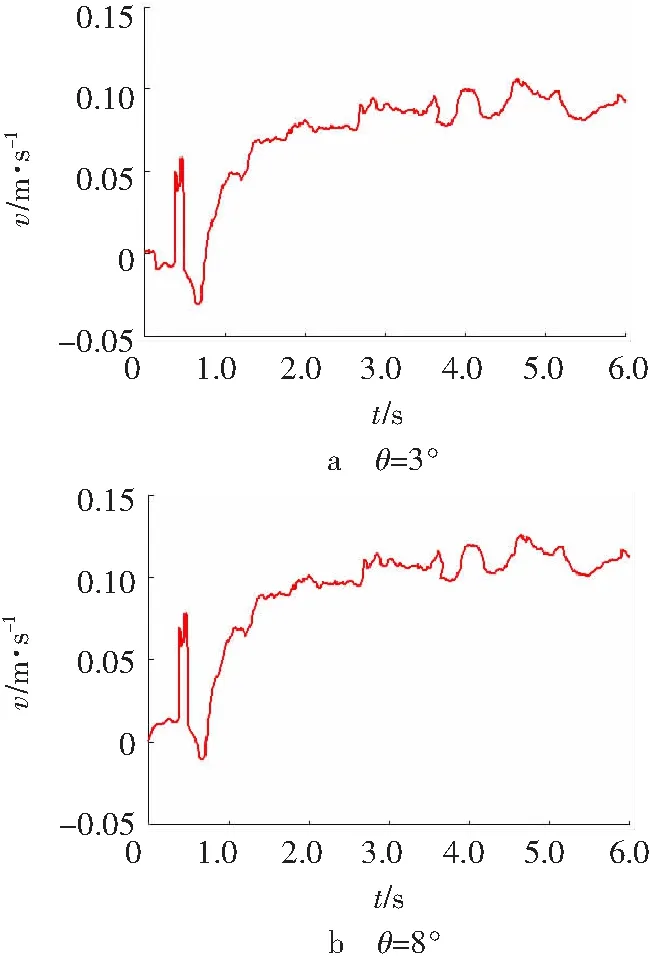
图13　不同的转弯角度下转弯处输送带的横向位移

Fig. 13Lateral displacement at turn of conveyor belt under different turning angle

(3)转弯半径的减小导致转弯处输送带的横向偏移量加大,转弯半径减小到一定程度后输送带可能会离开托辊而导致输送机的自然导向转弯无法实现。

(4)输送带的张力及转弯处输送带在横向的偏移量，随着转弯角度的增大而增加,大角度转弯会降低输送机的稳定性。

[1]杜海彬, 程相文. 平面转弯带式输送机转弯段的受力模型分析[J]. 矿山机械, 2010, 38(15): 83-87.

[2]李王飞, 赵波, 童景琳. 平面转弯带式输送机转弯段的优化设计[J]. 煤矿机械, 2012, 33(10): 10-12.

[3]任惠英, 高玉莹. 平面转弯带式输送机技术方案浅析[J]. 矿山机械, 2011, 39(9): 52-56.

[4]朴香兰. 长距离平面转弯带式输送机关键设计技术研究[D]. 长春: 吉林大学, 2010.

[5]郝文光. 带式输送机的动态设计与实践[J]. 煤炭加工与综合利用, 2012(4): 30-32.

[6]刘艳妮. 大倾角带式输送机的动态分析[D]. 青岛: 山东科技大学, 2011.

[7]牛巍巍. 带式输送机的动态分析研究[D]. 太原: 太原科技大学, 2010.

[8]郝双双. 动态特性对带式输送机运行安全性的影响研究[D]. 哈尔滨: 黑龙江科技学院, 2008.

[9]孙文涛. 线摩擦驱动带式输送机动态分析[D]. 哈尔滨: 黑龙江科技学院, 2012.

[10]韩瑞飞. 辊子压带式带式输送机的动态特性分析[D]. 哈尔滨: 黑龙江科技大学, 2013.

[11]LI D G，LIU C S. Development and experiment of cutting force model on conical pick cutting rock at different wedge angles[C]// Proceedings of the 2015 International Conference on Mechanics and Mechatronics. Singapore: World Science, 2015:11-18.

[12]LI D G，LIU C S. Conical pick cutting experiment and resistance spectrum characteristics[C]// Proceedings of the 2015 International Conference on Mechanics and Mechatronics. Singapore: World Science, 2015: 19-25.

[13]卜培培. 平面转弯带式输送机转弯段参数分析及动态仿真[D]. 太原: 太原科技大学, 2012.

[14]李晓辉. 平面转弯带式输送机动态特性分析[D]. 哈尔滨: 黑龙江科技大学, 2015.

(编辑徐岩)

Dynamic characteristics analysis of belt conveyor with horizontal curves based on ADAMS

LIYangxing，LIXiaohui

(School of Mechanical Engineering, Heilongjiang University of Science & Technology, Harbin 150022, China)

This paper is prompted by a specific solution to problems occurring in belt conveyor, such as the dynamic characteristics-an important factor affecting the operation of belt conveyor-due to the enlargement of the scope of application of belt conveyor and belt speed increase; the curve layout imposed on belt conveyor due to negative effect on transportation routes by the landform and obstacles including buildings; and a greater influence of operation parameters and roller structural layout in turning section on stable operation of belt conveyor and is necessitated by a novel study on the dynamic characteristics of large high-speed belt conveyor with horizontal curves. This study consists of utilizing Pro/E to build belt conveyor with horizontal curves; applying dynamics analysis software ADAMS to develop virtual prototype model; and analyzing the influence of running speed, conveyor belt stiffness, bending radius and the turning angle on dynamic characteristics of belt conveyor with horizontal curves . The result show that an increase in the stiffness of the conveyor belt leads to a reduction in the peak of belt tension and offset in the startup process, and a greater stability of the operation; belt tension and turning offset increases due to an increase in the turning point, and large turning angle triggers a reduced stability of the conveyor belt.

belt conveyor; horizontal curves; dynamic characteristics

2015-08-06

李阳星(1961-),女,辽宁省西丰人,教授,研究方向:现代设计法,E-mail:lyxcome@ 163.com。

10.3969/j.issn.2095-7262.2015.05.004

TD528

2095-7262(2015)05-0482-07

A