五轴加工刀具矢量压缩平滑定向插补算法研究*

田军锋，范素娟，左宪禹

（河南大学a.计算机与信息工程学院；b.信息化管理办公室，河南开封 475004）

五轴加工刀具矢量压缩平滑定向插补算法研究*

田军锋a，范素娟b，左宪禹a

（河南大学a.计算机与信息工程学院；b.信息化管理办公室，河南开封 475004）

为解决五轴加工中刀具矢量变化不均匀引起减速和加速的反复发生，带来加工形状变得粗糙和加工时间变长的问题，提出一种刀具矢量压缩平滑定向插补算法。通过对指令程序进行压缩处理，可以去除刀位点和刀具矢量变化小的指令，对刀具矢量平滑处理，可以使得刀具矢量的变化与线性轴的变化一致，定向插补是对优化后的指令刀位点数据和刀具方向进行插补计算，以实现高速加工。通过仿真实验验证了该算法的有效性和可行性。

五轴加工；压缩平滑；刀具矢量；定向插补

0 引言

五轴联动数控加工是为了克服三轴加工的不足而发展起来的一项先进制造技术，在提高加工质量、降低加工成本和减少加工时间等方面有着明显的优势。通过增加两个旋转轴，使得加工的灵活性大大增强，增加的旋转轴可以使得刀具定位在空间任意方向，但是也带来了运动过程中刀具矢量较难控制的问题［1-3］。

五轴加工程序一般是由计算机辅助制造（Computer Aided Manufacturing，CAM）系统通常将计算机辅助设计（Computer Aided Design，CAD）系统设计生成的加工曲面用大量微小三角平面逼近，并在特定的容差范围内用一系列折线去覆盖这些三角平面，从而生成大量指令点构成的数控加工程序［4］，同时，刀具矢量被定义为三角平面的垂直方向，在三角平面边界处的刀位点的刀具方向定义为相邻三角平面垂直方向的平均值。刀具矢量可能会在刀端点（Tool Control Point）路径长度短的程序块处发生较大变化，另一方面，刀具矢量的变化与线性轴的变化不成比例。如果数控机床直接加工这样的程序指令，则机床转动轴会发生反复的减速和加速运动，造成加工曲面质量下降和加工时间延长，从而不利于高速和高表面质量的加工［5-6］。对指令程序中刀位点数据和刀具矢量数据进行处理是实现高速和高效加工的前提，对刀具矢量的变化要考虑机床的运动学特性，对刀具矢量的优化方法的研究具有重要的理论和应用价值。近年来，众多学者在五轴加工刀具矢量的控制和优化上进行了大量的研究。在参考文献［7-10］提出了不同的方法来光顺五轴旋转轴的运动。文献［7］和文献［8］都是根据四元数对刀具矢量进行光顺。文献［9］给出了C-space下满足机床运动学条件的刀具矢量光顺算法。文献［10-11］提出了根据运动学性能优化刀具矢量的方法。但以上方法都没有对刀位数据和刀轴矢量同时进行优化和处理。

基于以上研究和分析，本文提出了一种刀具矢量压缩平滑定向插补方法。该算法能够对生成的指令程序进行压缩和平滑处理，然后对优化后的指令进行定向插补，从而达到提高加工表面质量和缩短加工时间的目的。

1 压缩平滑定向插补算法

压缩平滑定向插补算法的基本思想是先对生成的指令数据进行压缩处理，把满足容差限制的微小变化指令去除，简化指令程序容量，然后对压缩生成的指令中的刀具矢量进行平滑处理，使得旋转轴和线性轴在相邻指令间变化成比例，最后对平滑后的指令进行定向插补来实现高速和高表面质量加工，能够使加工形状圆滑从而缩短加工时间。

1.1 指令压缩

程序指令包含刀位点数据p（x，y，z），刀轴矢量v（i，j，k）两部分。对于每一个连续微小线段加工区域，刀位点数据和刀轴矢量变化量可能在系统容差范围内，则根据下面的方法可以将这些指令删除，减小指令代码量。

指令压缩需要满足两个条件：

条件一：后继某刀触点位置处的刀轴矢量与初始刀触点位置Ps处的刀轴矢量所成角度α在旋转角度容差θ范围内。

条件二：后继某刀触点位置到特定直线的距离d在线性轴距离容差D内，特定直线是指连接加工开始刀触位置点Ps和不满足条件一对应的刀触位置点Pe。

首先根据刀轴矢量与初始刀轴矢量之间夹角大小进行划分，当刀轴矢量方向变化量α小于系统角度容差θ时，将这些指令点作为下一步候选指令点进一步处理，继续处理下一个刀轴矢量；如果大于系统角度容差，则直接输出这些指令点。接下来计算候选指令点到直线的距离d，该直线是由初始刀轴矢量点和刀轴矢量变化量大于角度容差的指令点连线。

如果d小于线性轴容差D，则该候选指令点可以删除，继续计算下一个候选指令点到前一直线的距离，进行判断。否则，更新直线的另一端点为该候选指令点，并重新开始计算该线段内的候选指令点到该新的直线的距离。当该直线内的候选指令点处理完，则更新初始刀轴矢量为最新输出的刀轴矢量，继续进行上述操作直到整个程序结束。这部分功能主要是对刀位点数据和刀轴矢量进行去除，删除掉刀具的微小晃动指令。而源指令中的进给速度等辅助指令仍旧保留。

对应图1所示，由编程指令点Pi-1、Pi、Pi+1和Pi+2构成的一段加工路径，对应的刀轴矢量方向分别是Vi-1、Vi、Vi+1和Vi+2。

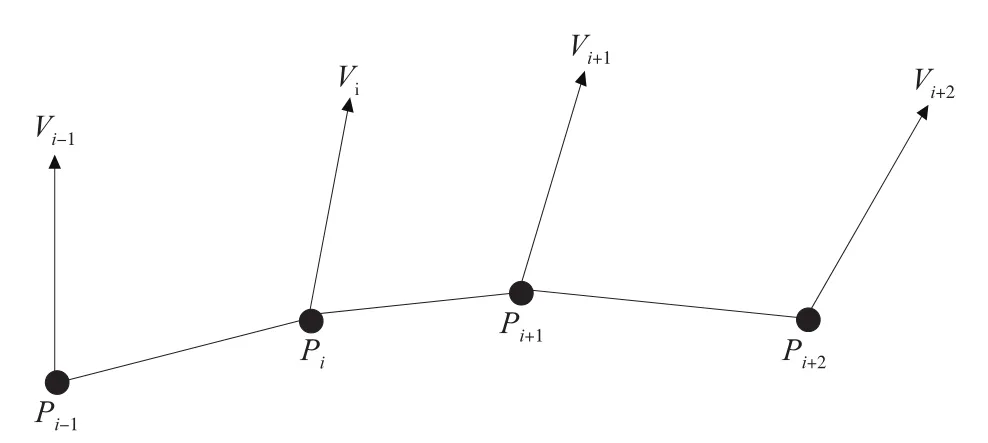
图1 加工程序指令点和对应刀轴矢量

图2 加工程序指令点及旋转角度容差苑围

1.2 指令压缩算法

对图1所示，由编程指令点包括刀触点数据和刀轴矢量数据构成的微小线段加工区域，在每一个编程指令点都有一个指令点容差范围D和旋转角度容差范围θ，如图2所示。通过图3所示的指令压缩算法流程便能将符合条件一和条件二的微小晃动指令去除。详细步骤如下：

（1）首先是进行初始化操作，初始化当前下标i值为1和初始刀轴矢量下标s的值为1。并对旋转轴容差θ和线性轴容差D进行赋值。

（2）判断第i个编程指令点是否能够成功读取。若读取失败，则整个算法结束。如果成功读取，转入步骤（3）。

（3）将当前下标i的值增加1，转入步骤（4）。

（4）判断当前新的第i个编程指令点是否能够成功读取。若读取失败，说明到了程序段结尾，需要对前面成功读取的数据进行处理，将i值减1，然后转入步骤（6）。若读取成功，计算当前刀触点处刀轴矢量与设定初始刀触点处刀轴矢量间夹角α值，转入步骤（5）。

（5）判断α与旋转角度容差θ大小；若α＜θ，则表明当前刀触点的刀轴矢量与初始刀轴矢量间夹角小于系统容差θ，则转入步骤（3）。若α≥θ，则表明当前刀触点的刀轴矢量与初始刀轴矢量间夹角超过了系统容差θ，转入步骤（6）。

（6）将结束刀触点刀轴矢量对应下标e更新为i，将候选待处理刀轴矢量下标k赋初始值为s。转入步骤（7）。

（7）将k值加1，在区间s与e之间对候选指令点做进一步处理。

（8）判断变量k与e的大小。若k≥e，转入步骤（9）；若k＜e，计算刀触点Pk到直线的距离d，求出d值。转入步骤（10）；

（9）更新初始刀轴矢量下标s的值为e，当前下标i的值为s，同时输出当前下标为s的指令点的数据，包括Ps和Vs。转入步骤（2）。

（10）判断d与线性轴容差D的大小。若d＜D，转入步骤（7）；若d≥D，说明当前指令点的刀触点到直线的距离超过了线性轴容差D的限制，需要往前回溯重新对之前的候选指令点进行判断。更新候选指令点的结束下标e为当前候选指令点下标k，当前候选指令点下标k值更新为初始刀轴矢量下标s值，转入步骤（7）。

1.3 刀具矢量平滑

刀具矢量平滑处理，转动轴位置指令校正抑制每个程序块中相应的旋转轴速度的震荡。首先要设定每次调整的最大程序段数N，算法先对指令中的刀位点线性轴变化量进行计算，计算程序段中每一个刀位点到段首与断尾直线距离之比，比值由公式（1）求出。

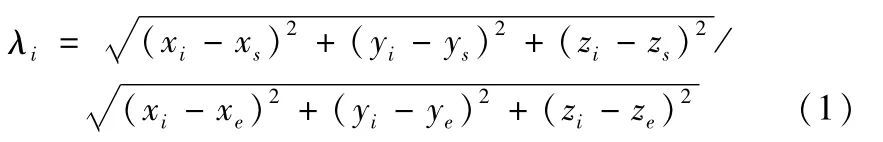
然后，根据每一个刀位点计算出的比值，利用公式（2）～（4）求出平滑后的刀具矢量。

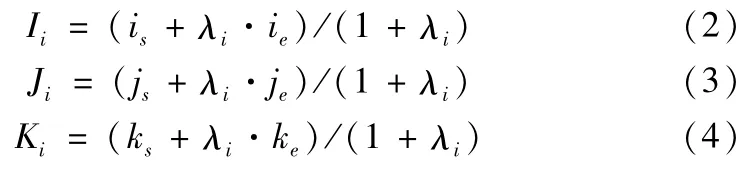
图3 指令压缩算法流程

式中，（xs，ys，zs），（xe，ye，ze），（is，js，ks）和（ie，je，ke）分别表示第一段和最后一段对应的刀位点数据和刀具矢量，（Ii，Ji，Ki）表示对第i个刀具矢量平滑后对应的刀具矢量，i取值范围是2～N-1。这部分主要功能是对刀具矢量进行调整，使得刀具矢量变化与线性轴变化成比例，提高加工速度，缩短加工时间。

1.4 定向插补

本文以AC双转台五轴机床作为研究对象，其中A和C分别表示绕机床X轴和Z轴旋转的旋转坐标轴。将工件坐标系下的刀位点数据（xi，yi，zi）和刀具矢量（Ii，Ji，Ki）转换成双转台机床坐标系下的坐标（Xi，Yi，Zi，Ai，Ci），工件坐标系与机床坐标系转换关系如公式（5）～（9）所示。

其中：（tx，ty，tz）为A轴中心到工件坐标系原点的长度补偿量。

定向插补包括机床坐标系下刀位点插补和旋转角度插补，针对指令压缩平滑后工件坐标系下程序指令经公式（5）～（9）转换为机床坐标系下坐标进行插补，在每一个插补周期Δt计算插补刀位点坐标和旋转角度。刀位点在每一个插补周期的运动位移s由公式（10）求出

其中，Δt表示插补周期，F表示进给速度。在相邻指令间隔刀位点总的运动位移S由公式（11）求出

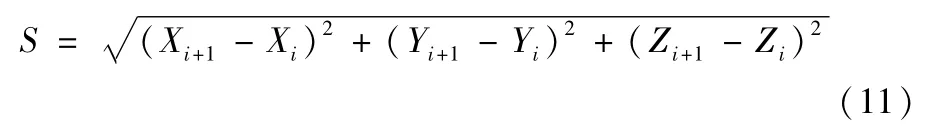
则新的刀位点插补位置由公式（12）～（14）求出

其中，j的取值范围是0～n-1，n=S/s，（X0，Y0，Z0）=（Xi，Yi，Zi），（Xn，Yn，Zn）=（Xi+1，Yi+1，Zi+1）。

旋转角插补：为了使插补点的旋转角和刀位点的变化成比例，首先计算每一个插补周期线性轴的变化比例K2，该值由公式（15）求出。

新的旋转角插补位置由公式（16）～（17）求出

2 仿真实验及性能分析

为验证本文算法的正确性，对表1中的刀位数据和刀具矢量进行仿真实验，图4所示为表1中刀位点组成的编程轨迹。仿真实验中设定进给速度为500mm/min，主轴转速3000r/min，插补周期Δt=2ms，最大刀具矢量容差θ=0.001rad，最大线性轴容差D=0.01mm。

表1 原始刀位点数据和刀具矢量

图4 待加工刀具轨迹

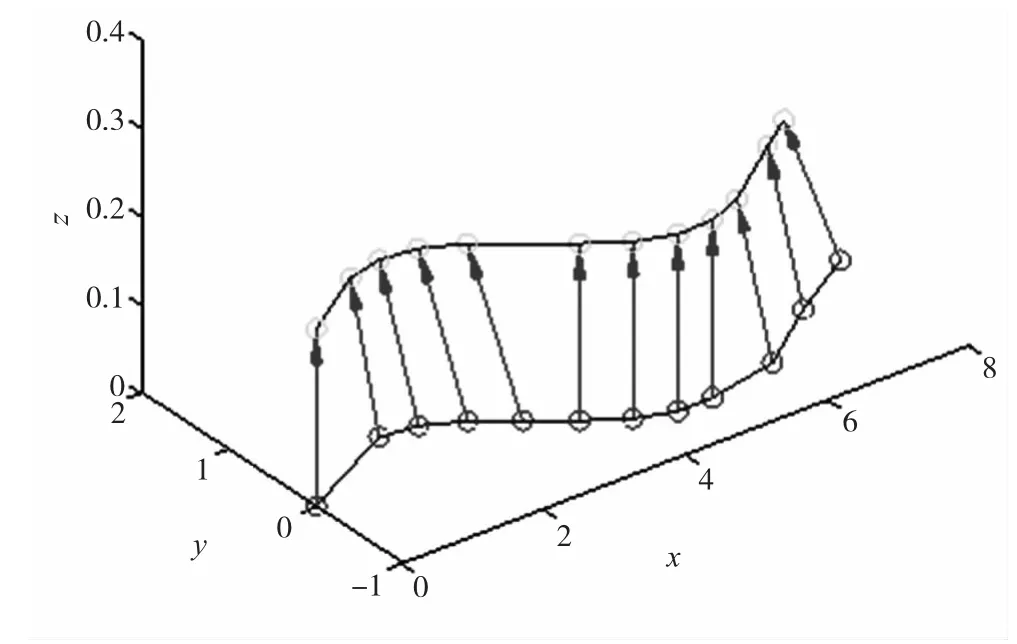
图5 压缩后刀位点和刀具矢量

图6 平滑后刀具矢量

图7 对应的旋转轴速度

根据指令压缩方法对表1中的刀位点数据和刀具矢量数据进行压缩处理，得到压缩后的刀位点和刀具矢量如图5所示，从图中可以看出满足系统容差限制的刀位点和刀具矢量被去除，也即去除掉了刀具小的晃动。对压缩后的指令进行刀具矢量平滑处理，平滑后的刀具矢量如图6所示，从图中可以看出，蓝色虚箭头是调整后的刀具矢量，调整后的刀具矢量变化更加平滑，与线性轴的运动也成比例变化。最后将压缩平滑后的指令转换成双转台五轴机床坐标，对机床坐标系下的刀位点数据和旋转角数据进行定向插补，插补原理是使得线性轴与旋转轴变化成比例，插补后的旋转速度时间曲线如图7所示，不进行压缩平滑处理的轨迹如曲线1所示，仅进行压缩平滑而不进行定向插补轨迹曲线2所示，进行压缩平滑定向插补轨迹如曲线3所示。从图7可以看出，算法不仅使得刀具矢量变化更加平滑，而且加工速度得到了提高，缩短了加工时间。

3 结论

五轴加工可以显著提高加工效率，由于旋转轴的变化灵活可以定位在空间任意方向，刀具方向变化和刀位点变化不成比例引起机床反复加减速，使得加工表面粗糙和加工时间延长。对此，本文提出了一种刀具矢量压缩平滑定向插补算法。该算法先对由CAD/CAM生成的五轴数控加工程序进行优化，对于刀位点和刀方向变化小的指令去除，消除了刀具小的晃动对加工造成的负面影响。同时对刀具矢量进行平滑处理，获得平滑的加工形状。最后对优化后的指令进行定向插补。仿真实验表明，该算法可以使得刀具方向变化平滑，提高加工速度，获得平滑加工面，并缩短加工时间。

［1］罗明，吴宝海，李山，等.自由曲面五轴加工刀轴矢量的运动学优化方法［J］.机械工程学报，2009，45（9）：158-163.

［2］LIU Gu-ran.Thid-order local contact and application in 5-axis machining of sculptured surfaces［J］.Chinese Journal of Mechanical Engineering，2006，19（2）：265-267.

［3］CHEN Li-ping，CHEN Yan，HU De-jin.Interference-free tool posture generation for 5-axis NC milling free-form surfaces［J］.Chinese Journal of Mechanical Engineering，2004，17（3）：381-384.［4］VICKERSGW，BRADLEY C.Curved surface machining through circular arc interpolation［J］.Computer in Industry，1992，19（33）：329-337.

［5］ERKORMAZ K，ALTINASY.High speed CNC system desigh part II：Modeling and identification of feed drives［J］. International Journal of Machine Tools and Manufacture，2001，41（8）：1487-1509.

［6］叶佩青，赵慎良.微小线段的连续插补控制算法研究［J］.中国机械工程，2004，15（15）：1354-1356.

［7］HOM C，HWANG CH，HU CH.Five-axis tool orientation smoothing using quaternion interpolation algorithm［J］.International Journal of Machine Tools and Manufacture，2003，43（12）：1259-1267.

［8］张小明，朱利民，丁 汉，等.五轴加工刀具姿态球面NURBS曲线设计及优化［J］.机械工程学报，2010，46（17）：140-144.

［9］JUN CS，CHA K，LEE Y S.Optimizing tool orientations for 5-axis machining by configuration-space search method［J］. Computer Aided Design，2003，35（6）：549-566.

［10］CASTAGNETTIC，DUCE，RAY P.The domain of admissible orientation concept：A new method for five-axis tool path optimization［J］.Computer Aided Design，2008，40（9）：938-950.

［11］A.Yuen，K.Zhang，Y.Altintas.Smooth trajectory generation for five-axis machine tools.International Journal of Machine Tools&Manufacture，2013，71：11-19.

Research on Compression Smooth Orientation Interpolation of Tool Posture Vector in Five-axis Machining

TIAN Jun-fenga，FAN Su-juanb，ZUO Xian-yua
（a.School of Computer and Information Engineering；b.Information Management Office，Henan University，Kaifeng Henan 475004，China）

To solve problems that the machined shape becomes rough and the machining time becomes long in five-axis machining posed by deceleration and acceleration are repeated due to uneven change of the tool posture vector.A compression smooth orientation interpolation of tool posture vector was developed.A program command to a block having small changes in a tool center point position and a tool posture vector was removed by compression process.Tool posture vector command was smoothed to attain a change of tool posture vector in proportion with that of the linear axis command.The orientation interpolation is performed on the optimal commands processed by compression smooth to achieve a high speed machining.A simulation test was performed to verify the effectiveness and feasibility of this algorithm.

five-axis machining；compression smooth；tool posture vector；orientation interpolation

TH165；TG659

A

1001-2265（2015）04-0104-04 DOI：10.13462/j.cnki.mmtamt.2015.04.027

2014-06-10；

2014-07-18

国家自然科学基金项目（61202098）

田军锋（1980—），男，河南叶县人，河南大学讲师，博士，研究方向为高档数控技术，（E-mail）tianjunfeng@henu.edu.cn。